Python语言在大学物理实验数据分析中的应用

牛相宏，潘乘风，陈 伟，李兴鳌

(南京邮电大学 理学院，江苏 南京 210023)

随着现代电子信息技术的飞速发展，Java、C++、Python等计算机编程语言在大学课程中的应用愈加普遍。同时随着理论与实验的不断融合，《大学物理实验》课程所涉及的实验内容更加前沿与广泛，部分实验涉及的参数较多、实验数据冗杂，分析精度也不断提高。能够科学有效地使用科学软件对实验数据进行准确地处理，理解实验中蕴含的物理意义也是《大学物理实验》教学目的之一。Python是一种开源免费的程序设计语言，其扩展库中的numpy、matlotlib、sklearn等，提供了相应的方法用以实现数据拟合和图像可视化。因其具有面向对象、支持动态语义、内置高级数据结构、语法简洁优美等优点，Python在日常学习和科学研究中得到十分广泛的应用。通过对Python语言的学习，掌握可编程的数据可视化、不同方式下的数据拟合，能够加深学生对于大学物理实验中相关理论知识的理解，进一步培养学生利用现代科学技术不断探索的创新意识，为其今后的课程学习和科研工作打下坚实的基础。

1 Python语言在大学物理实验数据处理中的实践

Python作为一门功能强大的计算机编程语言，迄今为止已经发展得较为完善。Python在软件设计、工业生产、自动化应用等方面展现出独特的魅力，但在《大学物理实验》课程中的应用却寥寥无几。本文对Python语言如何处理实验数据作详细的讨论。首先以《受迫振动》实验为引例，介绍如何利用Python语言对其实验数据快速地进行可视化处理；随后通过《电介质介电常数的测量》以及《热敏电阻和温差电动势的测量》两个实验分别介绍了线性拟合和对数拟合的操作方法，在每个实验中均附上运行代码，同时可以根据程序设计的“拟合参数”对拟合结果进行有效评价。

1.1 Python图像可视化—以《受迫振动的研究》实验为例

作图法是《大学物理实验》课程中数据处理的一种基本方法。该传统方法利用坐标纸手工绘图处理数据，仅适用于自变量和因变量呈简单线性关系这一情况。当实验数据样本参数多以及呈现出非线性等复杂情况时，利用科学软件对其进行可视化处理，便可以得到既方便又可靠的结果。对这样冗杂的实验数据若仍采取坐标纸绘图的方法，极有可能由于人为误差，例如作图不规范等导致某些关键物理量的错误或丢失。在自变量和因变量呈非线性函数关系的情况下，极值点、拐点、边界点等特殊点往往代表着物理特性的转变或相变等，这对于理解该实验蕴含的原理和内在机制起到至关重要的作用。而采用坐标纸手绘作图法会很容易在特殊数据点的连接上忽略甚至丢失这些关键的特征数据。利用Python语言进行实验数据可视化处理，不仅易于保存完整的实验数据，更有助于掌握当前实验结果以及理解其蕴含的物理机制。

在《受迫振动的研究》实验中，以表1中的数据为例：为了便于比较，实验要求在同一张纸上绘制出振幅θ、相位差φ随频率比ω/ω0变化的幅频曲线和相频曲线。利用Python语言及其内置的扩展库，可以方便快捷地完成实验要求。以下给出相关代码并对关键处给予注释：

import numpy as np

import matplotlib.pyplot as plt

from sklearn.metrics import r2_score

# 名称为x，y，z的列表中分别写入频率比ω/ω0、振幅θ、相位差φ实验数据。

x=[0.970，0.971，0.972，0.974，0.977，0.982，0.987，0.994，0.999，1.002，1.006，1.016，1.025，1.035，1.042，1.045]

y=[65，68，70，76，82，97，119，137，147，144，136，98，72，58，50，47]

z=[25，26，27，30，32，40，50,69，87，99，113，137，149，155，159，161]

# 使用numpy中的一种方法建立多项式模型。

model_1=np.poly1d(np.polyfit(x，y，10))

model_2=np.poly1d(np.polyfit(x，z，10))

# 指定行的显示方式，从0.970开始至1.045结束。

line_1=np.linspace(0.970，1.045，100)

line_2=np.linspace(0.970，1.045，100)

# 用r-squared的值来衡量多项式回归拟合度，r平方的数值范围属于0-1，其中0表示不相关，而1则表示完全相关。

print(r2_score(y，model_1(x)))

print(r2_score(z，model_2(x)))

# 绘制散点图

plt.scatter(x，y)

plt.scatter(x，z)

# 画出多项式回归线

plt.plot(line_1，model_1(line_1)，label="θ")

plt.plot(line_2，model_2(line_2)，label="ψ")

plt.legend()

# 显示

plt.show()

如图1所示，运行代码可以成功绘制出两条符合实验要求的曲线，充分体现了Python语言在可视化数据作图中的优越性。从控制台输出的内容可以发现两次拟合的r-squared的值分别为0.999 36、0.999 66，这也充分说明了程序给出的可视化图像是足够准确的。不仅如此，代码运行后生成的窗体还支持光标获取曲线上任意点的数值，这对数据分析和实验结果的理解也是大有裨益。根据处理后的图像显示，当ω/ω0在1附近时，产生共振现象(振幅达到最大值，相位差φ=90°)。表1为测得的相应实验数据。

图1 《受迫振动的研究》实验中的幅频曲线和相频曲线

表1 《受迫振动》实验数据

1.2 Python线性拟合—以《电介质介电常数测量》实验为例

利用电桥法测量固体材料的介电常数εr，测得固体电介质样品直径d，电介质面积s=πd2/4，电介质厚度l，电容极板面积s0=2 158 mm2，极板间距D=5.000 mm。C串=εrε0s/[l+εr(D-l)]表示样品面积范围内电容和空气层电容串联得到的电容量；C0=ε0s/D表示以空气为介质所对应的电容量；C分表示测量时引线及系统引发的分布电容之和；C边表示固体电介质面积以外的板极电容量和边界电容量之和。当极板间介质为空气和固体电介质时，分别测量其电容，两次测量过程中保持极板间距和系统状态不变，故以空气为介质下的电容量Cair可以表示为Cair=C0+C边+C分，放入固体电介质下的电容量Cr可以表示为Cr=C串+C边+C分。处理一下，可以得到固体电介质相对介电常数εr的表达式如下：εr=l(Cr-Cair+ε0s/D)/[ε0s-(Cr-Cair+ε0s/D)(D-l)]

为了减小实验误差，采用多次测量取平均值的方法对相关参数进行测量，表2为测得的相应实验数据。在测量计算空气介电常数和系统分布电容过程中，不断增加极板间距并测量其相应的电容量，表3为测得的相应实验数据。

表2 固体电介质介电常数测量的实验数据

表3 空气介电常数和系统分布电容测量的实验数据

import matplotlib.pyplot as plt

from scipy import stats

import numpy as np

x=[]

x_=[1.00，1.10，1.20，1.30，1.40，1.50，1.60，1.70，1.80，1.90]

y=[33.12，31.56，30.18，29.11，28.16，27.14，26.38，25.72，25.14，24.60]

for i in x_:

x.append(1/i)

# 建立线性拟合模型

slope，intercept，r，p，std_err=stats.linregress(x，y)

def myfunc(x):

return slope * x + intercept

model=list(map(myfunc，x))

# 获取线性拟合后的各项系数并在控制台输出

coef=np.polyfit(x，y，1)

print(“各项系数为：”， coef)

print(r)

plt.scatter(x，y)

plt.plot(x，model，label="Linear Fitting")

plt.legend()

# 对x轴，y轴进行标签

name_x=plt.xlabel("d(mm)")

name_y=plt.ylabel("C(pF)")

# 显示

plt.show()

如图2所示，得到线性拟合的结果。r-squared=0.999 8，说明拟合效果非常好。同时可以在控制台上得到输出的关于线性拟合的系数分别为18.089、15.109，即ε0s0=18.09，C分=15.11。据此可以求得ε0=8.382×10-3pF/mm，将ε0带入εr的表达式中，求得固体电介质的相对介电常数εr=4.157。将这一数据和手绘作图得到的固体电介质相对介电常数4.266相比，差距明显，这是因为手动拟合人为不可控因素过多导致的较大误差，精度远远不及计算机拟合的高精度。从结果上看，利用Python及其自带的扩展库对实验数据进行拟合，不仅节约时间、提高准确率，并且在精确度上也有极大的提升。

d/mm

1.3 Python对数拟合—以《热敏电阻和温差电动势的测量》实验为例

在一些物理实验中，所关注的物理量和待测量之间可能既不存在线性关系也不存在多项式关系的情况，如果直接对实验数据进行处理可能会造成结果失真。当所求物理量和待测量之间仅存在指数关系时，依据对数分析则可以简化处理过程，起到事半功倍的效果。

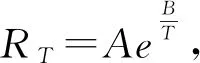
保持其他状态不变，测得不同温度下的热敏电阻阻值RT，表4记录了相关实验数据。同样地，利用Python可以迅速地得到拟合结果，运行代码及注释如下：

表4 《热敏电阻和温差电动势的测量》中阻值随温度变化实验数据

import matplotlib.pyplot as plt

from scipy import stats

import numpy as np

x=[]

y=[]

x_=[30，35，40，45，50，55，60，65，70]

y_=[1933，1301，970，775，627，540，459，408，372]

for i in x_:

x.append(1/i)

for j in y_:

y.append(np.log(j))

slope，intercept，r，p，std_err=stats.linregress(x，y)

def myfunc(x):

return slope * x + intercept

# 预测温度为75 ℃下的热敏电阻阻值并输出到控制台

R=myfunc(1/75)

print(np.exp(R))

model=list(map(myfunc，x))

# 获取线性拟合后的各项系数并在控制台输出

coef=np.polyfit(x，y，1)

print("各项系数为："， coef)

print(r)

plt.scatter(x，y)

plt.plot(x，model，label="Linear Fitting")

plt.legend()

# 对x轴，y轴进行标签

name_x=plt.xlabel("1/T/K")

name_y=plt.ylabel("lnR")

# 显示

plt.show()

如图3所示，从控制台输出的结果可以得到以下结论：B=86.80，lnA=4.69，即A=108.85，B=86.80。不仅如此，代码中还包含预测功能，上述给出的代码中预测了当温度T达到75 ℃时，热敏电阻阻值Rt=347.91 Ω。该功能使用起来也相当便捷，只需直接修改代码中“myfunc()”相关数值即可。显而易见，实现以上所有功能均依赖于Python语言中强大的数学扩展库。此外，还有更多有关数据处理，图像可视化等方面的功能有待在大学物理实验领域中开发与应用。

1/T/K

2 结 语

本文主要介绍了在大学物理实验中如何利用Python语言处理数据的一些基本方法，包括图像可视化、数据拟合等。利用功能日渐丰富的计算机编程语言对复杂实验数据的处理也变得简单便捷。利用Python语言及其自带的扩展库不仅可以实现基本的实验要求，而且能够根据需要增添一些额外的功能，例如精确获得具体点的函数值、对未知物理量的预测等等。在《大学物理实验》课程中引入Python语言，不仅实现了对实验数据的可视化作图，而且数据分析更加自动化、专业化。同时也能够加深学生对于大学物理实验及其相关知识的理解和把握，有利于培养学生严谨治学的态度和积极探索、踊跃创新的意识。将软件融于实验，将理论与实际结合，为学生今后的课程学习和科研工作打下坚实的基础。