基于路径搜索的配电网多端行波故障定位算法
游金梁,张帝,康童,朱哲明
(1.国网湖南省电力有限公司电力科学研究院,湖南 长沙410007;2.国网湖南省电力有限公司常德供电分公司,湖南 常德415000)
0 引言
配电网负荷越来越复杂,对供电可靠性的要求也越来越高,快速准确地故障定位显得愈发重要。然而配电网结构复杂,多为树形辐射状分布,馈线上分支多,且网络拓扑结构随经济建设经常发生改变,为配电网的准确定位带来了极大的挑战。
目前,现有的配电网故障定位方法从定位精度上可以分为故障区段定位和精确定位[1]。故障区段定位主要手段有基于FTU的区段定位、故障指示器以及基于TC的区段定位等。文献[2]利用FTU采集的暂态数据计算暂态零序电流相关系数、暂态零序电流有效值系数及暂态零序电流峰值与工频零序电流幅值之比等系数综合进行故障区段判断,准确率高,但定位区域大小主要取决于FTU的安装密度,人工巡线工作量依然很大。配电网故障精确定位方法主要分为阻抗法、S信号注入法和行波法[3]。文献[4-6]提出了利用节点阻抗矩阵进行故障定位,但是这些算法均没有考虑到配电网网络拓扑结构及负载的变化,难以保证定位精度,分支结构多的配电网存在故障点。S信号注入法通过向线路中人工注入特定信号,对其跟踪检测从而确定故障位置。一般需要停电操作,注入信号,且在高阻接地情况下能在非故障区流通,导致定位失败[7-8]。从原理上行波法可分为单端法和双端法。单端法是利用行波信号在阻抗不连续点的折反射特性,找到故障点的反射波,利用初始行波和反射波的时间差与波速计算故障距离。配电网线路复杂,行波折反射过程多,反射波头识别困难。双端法是利用初始行波波头到达线路两端的时间差与波速确定故障位置,不受故障类型、系统参数及运行方式等因素的影响,定位精度高,具有很好的发展前景。与输电线路不同,配电网分支多,结构复杂,需确定故障行波传输路径。文献[9]首先根据故障行波传播特性确定故障区段,再进行双端定位,这依然涉及到故障点反射波的检测。因此,国内外专家提出了以双端为基础的配网多端行波定位。文献[10-11]提出建立配电网的关联矩阵和距离矩阵,利用图论的方法排除伪故障点,最终利用双端理论确定故障位置,但都没有充分利用末端节点采集到的行波信息。文献[12-13]对故障行波到达配电网末端的时刻进行排序,通过时刻信息匹对配电网络进行搜索,确定故障位置,这些算法没有充分考虑配电网的网络结构,特别是在网络结构发生变化时,会导致定位失败。文献[14-15]尝试利用更少的行波测量装置进行故障定位,解决线路分支多、装置数量要求多的问题,但受环境及线路分支结构影响大,无法工程实用化。文献[16]将全网线路等分,事先建立各个节点到达末端节点的时间差矩阵,故障后建立故障到达时间差矩阵,通过比较故障前后行波到达时差矩阵的差异,通过矩阵差异值找出故障位置,实现故障定位。此方法的定位精度在很大程度上取决于线路等分密度,且计算十分复杂,不能适应网络拓扑结构的变化。
本文提出一种路径搜索的配电网多端行波故障定位算法,建立配电网网络拓扑结构的新矩阵表达形式,通过在矩阵中折线搜索,找出暂态故障行波的所有最短传输路径,综合配电网各个末端采集到的暂态行波信息实现故障点精确定位。
1 配电网网络拓扑建模
1.1 配电网网络拓扑结构图
配电网线路结构主要是树形辐射状,以某配电线路局部为例,从图论的角度可以将其表示为如图1所示。其中,A、B、C、D、E、F为配电网线路末端节点,包括电源节点和末端变压器节点;a、b、c、d为分支线路的交叉点,定义为分支节点,定义两节点间为一条线路。在该配电网中有6个末端节点,4个分支节点,共10个节点,9条线路。线路旁带下标字母表示线路编号,数字表示线路长度,单位为km。

图1 配电网网络拓扑结构图
1.2 配电网网络矩阵
对于具有n个节点,m条线路的配电网,可以用n×m的矩阵A表示,其行对应节点,列对应线路,称其为关联矩阵,记为A=(aij),矩阵中的元素定义aij为:

如图1所示的配电网,共10个节点,9条线路,用关联矩阵可表示为:
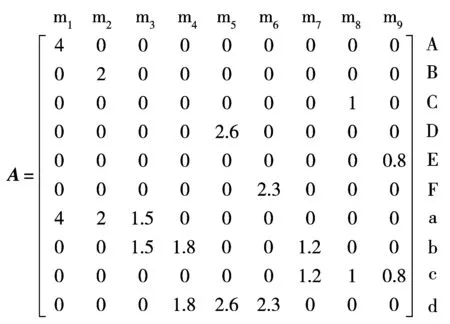
在矩阵中,每一列代表配电网中的一条线路,且只有两个相等的非零元素,非零元素所在行分别为配电网的节点;每一行代表一个节点,其中非零元素代表与该节点相连的线路,且末端节点所对应的行中只有一个非零元素,因为末端节点只与一条线路连接。
1.3 路径搜索
故障发生后,初始行波沿最短路径传播,在各个末端节点的行波检测装置上捕捉到初始波头信息。因此,需要确定各个末端节点间的最短路径。本文提出一种折线搜索的方式确定各末端节点间的最短路径,在配电网的关联矩阵中,可以很方便地进行路径搜索,找出暂态行波传输的最短路径。
首先选择一个末端节点,如末端节点A,在关联矩阵中找到该节点对应行中的非零元素(末端节点所对应的行中只有一个非零元素);以该非零元素为起点开始画竖线找到所在列中的另一个非零元素,然后以竖线末端为起点划横线;找到横线所在行的其他某一个非零元素,以该非零元素为起点继续画竖线,再画横线,保证所画横线方向总是朝着同一个方向的。重复以上步骤,直到出现另一个末端节点,其过程如图2所示。

图2 路径搜索示意图
图2 列出了从节点A点到节点C的最短路径,即竖线所在列代表的线路和横线所代表的节点:A→m1→a→m3→b→m7→c→m8→C。根据排列组合可知,具有a个末端节点的树形辐射状配电网,共有C2a条最短路径,图1所示配电网共有C26(15)条最短路径。
2 基于路径搜索的配电网定位算法
2.1 配电网线路归一化
配电网线路按结构可以分为架空线和电缆两种,暂态行波信号在这两种线路上的波速具有明显的区别。为了方便进行故障距离的计算,需对配电网线路进行归一化处理,即将电缆线路全部等效为架空线路,或将架空线路全部等效为电缆线路,具体可根据实际情况选择较少的线路将其等效。L1、L2分别为架空线和电缆线路的长度,v1、v2分别为暂态行波在架空线和电缆线路上的传播波速,则两者间的等效关系为:

若故障发生在归一化后的线路上,在确定故障距离Lf后,可通过反归一化得到实际故障距离L。
2.2 故障线路的确定
故障发生后,暂态初始行波信号将沿着最短路径传播,由于配电网线路存在分支线路,某两个末端节点间的最短路径可能不包括故障线路,如图3所示简化配电网。

图3 分支故障示意图
A、B、C为配电网的3个末端节点,LAC、LaB、Lac分别为配电网中的三条线路,L1、L2、L3也分别代表了对应线路的长度。若故障发生在Lac线路的点f处,对于A、B两个末端节点,最短路径为L1、L2,则Lac线路为A、B节点间的分支线路。若利用故障初始行波信号到达A、B节点的时刻进行故障定位,由D型行波测距原理可知:

式中,LA为故障点与A节点距离的计算值;LAB为A、B节点间的最短路径;TA、TB分别为故障初始行波到达A、B节点的时刻;v为行波波速。
在不考虑误差的理想情况下,LA与L1相等,即若故障未发生在某两个末端节点间的最短路径上,只能定位到分支节点附近,因此可以通过该判据判断故障是否发生在两末端节点间的最短路径上。由于在实际中总会存在误差,无法使LA与L1严格相等,故需设置一个合理的裕度δ,当满足式(3)时,判断故障未发生在A、B节点最短路径上,也即故障发生在a节点或分支线上。

但当选择B、C节点时,则可以判断故障发生在L3线路,也即总可以找到某两个末端端点使故障点位于其最短路径上。故确定故障线路的方法是:通过对配电网中所有末端节点(设为a个)两两排列组合,并通过折线搜索的方式确定最短路径及其所经过的线路,形成C2a个由节点和最短路径组成的节点组合。任选一个节点组合判断故障是否发生在最短路径上,若未发生在最短路径上,则继续判断下一组节点,直到确定故障发生的线路。若遍历所有节点组合,故障均未发生在最短路径上,则判定故障发生在分支节点,其流程如图4所示。
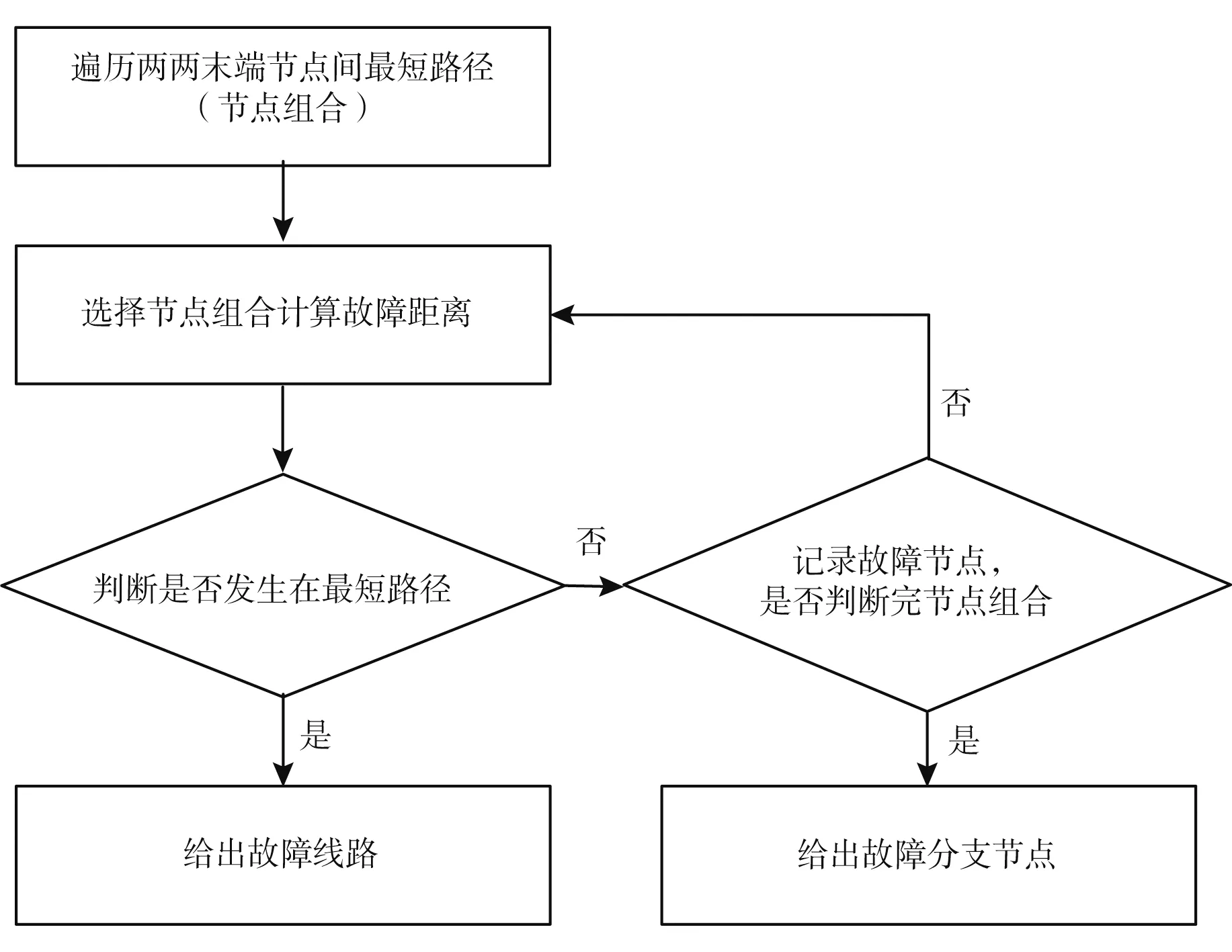
图4 故障线路的判定流程
2.3 故障定位结果综合计算
故障定位结果可以由双端行波定位方法给出,如式(2)。在配电网中,由于存在多个末端节点,故障线路往往会包含在多个最短路径中,综合利用多个末端节点的暂态行波信息,可以提高故障定位的准确度,也可对个别错误数据进行剔除,增强容错性。
对已确定的故障线路,可以取出包含故障线路的所有节点组合,设共有q组。则可计算出故障点距故障线路一端节点的距离,可由下式给出:
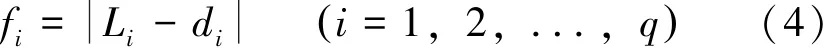
式中,di为通过节点组合计算出的故障点距末端节点的距离;Li为对应末端节点与故障线路一端节点的距离。
对fi进行筛选,剔除其中误差较大的数据,保留其中的均值,ε为设置的合理裕度)的fi数据,设共有个。则最终故障距离计算公式为:

2.4 配电网定位算法流程
基于以上分析,给出配电网多端行波故障定位算法,其流程如图5所示。
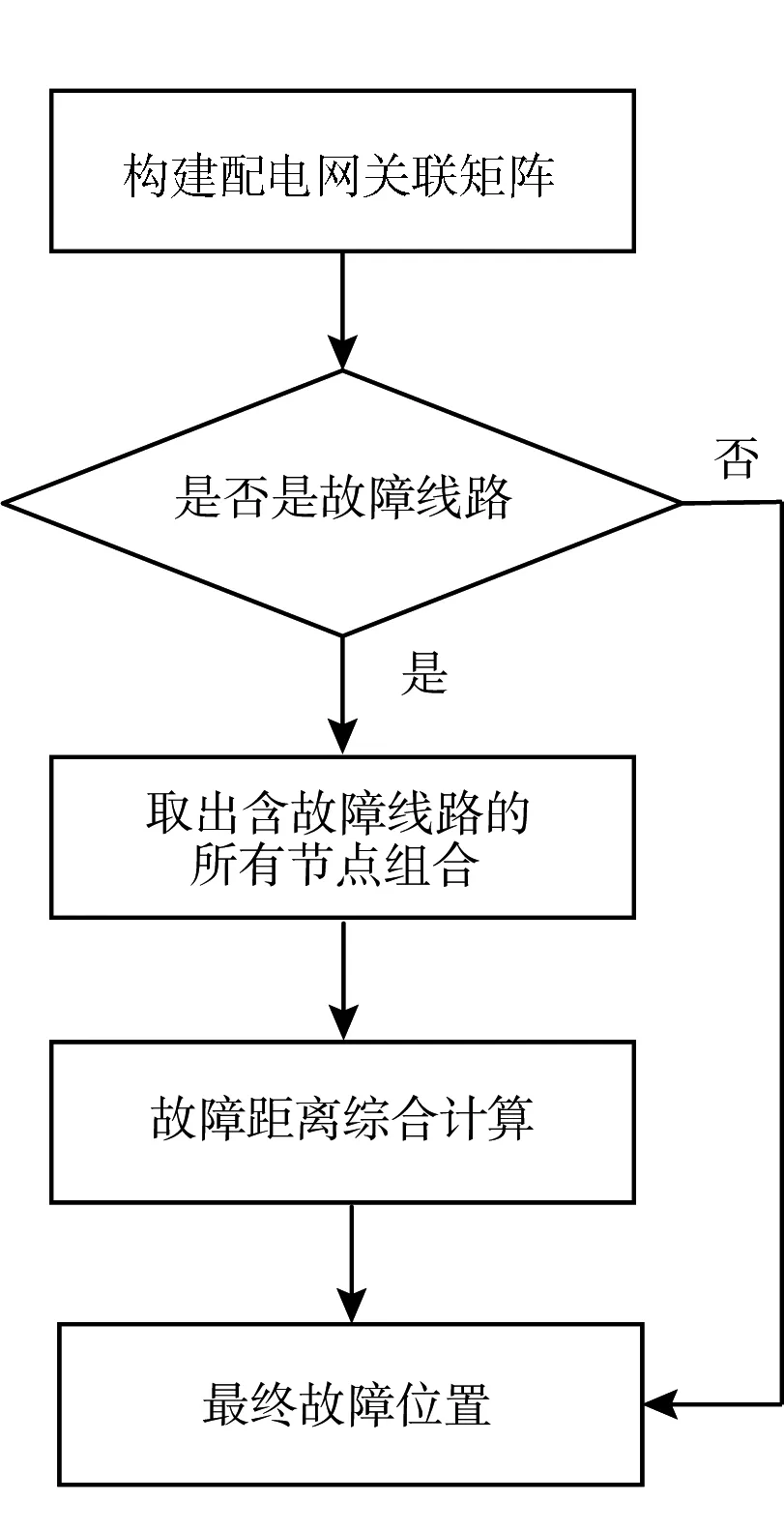
图5 故障定位流程图
其主要步骤为:1)基于配电网拓扑结构,建立关联矩阵,并进行路径搜索,形成节点组合,在配电网网络结构未发生变化时,此步骤无需重复;2)利用图5所示流程判断故障线路,若故障发生在分支节点,则直接给出故障位置及故障分支节点编号;若故障发生在线路上,则给出故障线路编号;3)取出包含故障线路的所有节点组合,对故障距离综合计算,给出故障位置。
3 仿真验证
利用PSCAD搭建10 kV单端电源供电的配网模型,如图1所示,其中A节点为电源,其余末端节点经由变压器后为负载供电。线路采用分布参数模型,电缆线路已折算为架空线路,通过仿真中线路参数计算出的波速为2.899×108m/s。各节点及线路对应关系见表1。
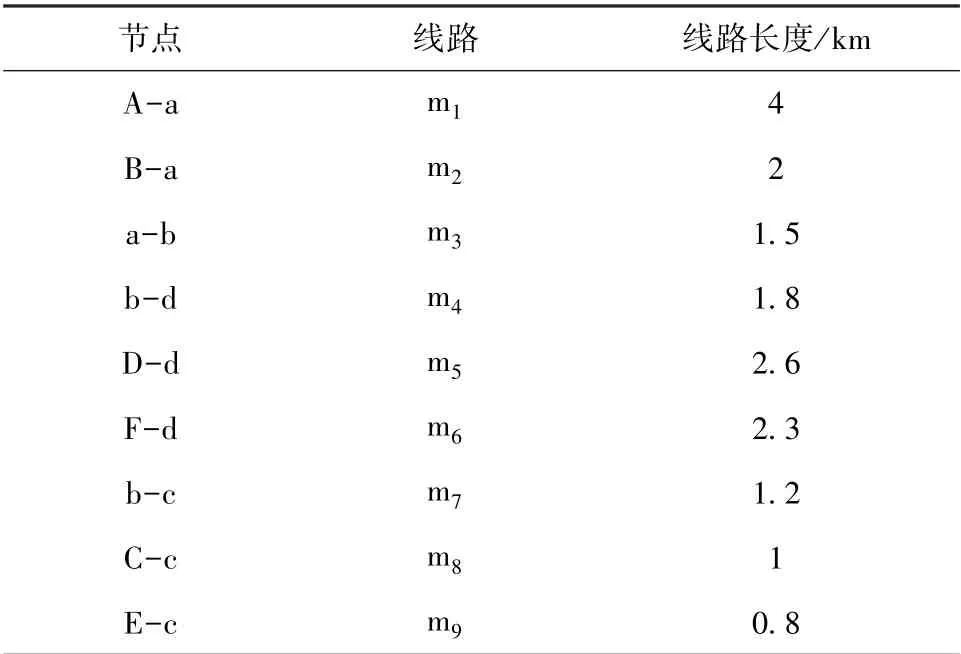
表1 配电网模型节点、线路对应表
行波采集装置安装在配网末端节点的变压器一次侧,负责采集和分析电流行波,其采样率为2 MHz。设置故障发生在距离A节点2 km处的f1点,故障类型为单相接地故障,对各末端节点采集到的电流行波信号进行相模变换后进行小波分析,得到初始波头时刻,见表2。

表2 各末端节点初始行波到达时间 μs
根据图4和图5所示的流程,对故障位置进行定位。图1所示配电网的节点组合共15组,即:


根据图4所示流程可以确定故障发生在m1线路上,筛选出包含m1线路的所有节点组合,为组合1)—5)。分别计算出故障距A节点的距离为2.058 km、2.038 km、2.051 km、2.083 km、2.046 km,利用式(4)—(5)给出最终故障定位结果为距离A节点2.054 km,与实际结果对比,误差为54 m。
若末端节点B的行波采集装置数据出现错误,得到的初始行波波头到达时间向后偏移了2μs,则通过节点组合1)计算出的故障距离为1.768 km,所有故障距离的平均值为1.997 km,通过计算的差值为0.229 2 km,由于采样率为2 MHz,取ε为150 m,可判断B节点为无效数据,剔除后给出的最终故障距离为2.054 km,误差为54 m。
由仿真结果可以得知,该算法可以实现配电网的准确定位,且具有一定的容错能力。路径搜索同时可以清晰地给出各末端节点间的最短路径及经过的线路和中间节点,在一定程度上实现了配电网的故障查找的直观性。
4 结语
本文提出一种基于路径搜索的配电网多端行波故障定位算法,仿真结果表明该方法可以快速准确地确定故障位置,且只需要在配电网的末端节点装设行波采集装置。配电网关联矩阵可以对配电网的拓扑结构进行清晰的描述,在配电网结构发生变化时,可方便简单地进行更新;路径搜索可以清晰地表达各末端节点间的最短路径。

