计及风速波动和频率约束的风电最大接入比例研究
鲁丁文,廖凯,沈阳武,王敏
(1.西南交通大学电气工程学院,四川 成都611756;2.国网湖南省电力有限公司电力科学研究院,湖南 长沙410007)
0 引言
近年来,以风电为代表的可再生能源渗透率不断提高,截至2020年底全球风电装机容量已超过700 GW[1]。随着风电装机容量的增大,电网惯性水平随之减小,但是风机对系统频率调节的贡献却为零,再加上风速的波动性以及间歇性,以至于电网系统频率问题突出,成为风电最大接入比例的约束条件,限制了风电装机容量的进一步提高[2]。因此,研究风机参与电力系统一次调频的控制方法对提高风电最大接入比例,增强风电消纳能力具有重要意义。
目前,风机参与电力系统一次调频控制的方法主要分为虚拟惯性控制及下垂控制,针对这两种控制策略,文献[3]通过结合下垂控制和虚拟惯性控制为电网提供频率支撑,改善频率特性,但该方法没有备用功率,可能引起额外的频率下降。文献[4-5]通过叶片桨距角减载控制,调节风机叶片角度以储存功率备用,为电网提供频率支撑,但该方法需要外部机械实现,灵活性较差,并且存在叶片磨损的问题。文献[6-7]通过转子速度减载控制、移动风机最大功率曲线以储存功率备用,为电网提供频率支撑,但该方法转子速度调节相对较慢,改善电网频率特性能力有限,无法在风速波动的情况下为电网提供较好的频率支撑。为抑制风速波动对电网频率的影响,文献[8-9]通过控制储能系统的充放电行为以抑制由风速波动引起的风能波动,进而改善风机调频效果,但该方法需花费高昂的投资成本及维护成本。
此外,在衡量风电最大接入比例的研究上,目前大多数文献[10-12]采用试凑法进行求解,虽然能够准确得到满足约束条件的风电最大接入比例,但需进行多次动态仿真实验,不断修正计算结果以满足约束条件,操作繁琐且当系统运行条件发生改变时还需重新操作。文献[13]以运行风险为约束,考虑风电场群并网时各风电场出力在时间上的随机性和空间上的相关性,提出了更加简便的风电最大接入比例计算方法,但该方法并未考虑电网频率约束条件。文献[14]基于IEEE9节点系统,考虑电网暂态稳定性及频率约束条件,通过分析风速的概率特性以求解风电最大接入比例,但该方法未考虑风机一次调频对电网系统频率的影响。文献[15-16]通过构建计及风电一次调频的电力系统频率响应模型,以系统稳态频率偏差及系统频率变化率为约束条件求解风电最大接入比例,但该方法并未考虑风速波动对电网系统频率的影响。基于以上文献分析发现,目前对同时计及风速波动和系统频率约束的风电最大接入比例计算方法的研究较少。
因此,为提高风电最大接入比例,本文提出一种基于虚拟滤波器的风机一次调频控制方法,其在不影响风机一次调频能力的基础上,结合虚拟滤波器抑制风速波动引起的频率波动,提高风机参与系统一次调频的效果,实现风电接入比例的提升。并且,为衡量提升效果,提出一种计及风速波动和频率约束的风电最大接入比例计算方法,进而对电网能够容纳的风电容量进行了量化。最后在Matlab/Simulink上搭建含风机的IEEE9节点系统进行仿真验证,仿真结果证明了所提计算方法及控制方法具有较好的准确性及有效性。
1 考虑风速波动的低阶系统频率响应模型
随着电力系统规模的不断发展,分析风电接入比例及风机一次调频对电力系统频率的影响也变得越来越复杂。因此,为简化分析,基于传统电力系统低阶系统频率响应模型,通过对具有一次调频能力的风机模型进行线性化,构建了如图1所示考虑风速波动的低阶系统频率响应模型。
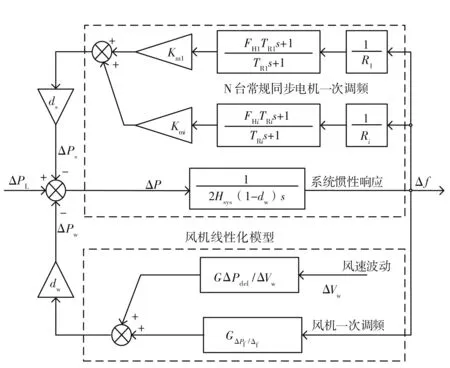
图1 考虑风速波动的低阶系统频率响应模型
在图1中,传统电力系统低阶系统频率响应模型能够反映电力系统在发生负荷波动时,常规同步电机的一次调频动态行为以及整个电力系统的系统惯性响应。风机线性化模型能够反映风机的一次调频能力以及风速波动对电力系统频率的影响。其中,dw及ds分别表示风机及常规同步电机的接入比例,因此该模型还可以简单方便地研究风电接入比例对电力系统频率的影响,以下将对这两部分进行详细介绍。
1.1 传统电力系统低阶系统频率响应模型
传统电力系统低阶系统频率响应模型包括常规同步电机一次调频及系统惯性响应两部分,其通过忽略常规同步电机蒸汽-涡轮调速器的非线性和除最大时间常数外的所有时间常数,使常规同步电机的惯性时间常数及再热时间常数主导电力系统频率响应,具有推导简单且结果准确的特点。
1.1.1 常规同步电机一次调频
如图1所示,其上半部分表示N台常规同步电机参与一次调频。其中,TRi、FHi、Kmi、Ri分别表示第i台汽轮机的再热器时间常数、高压锅炉输出功率所占比例、机械功率增益因数及调差系数。运用文献[17]所提方法对N台常规同步电机等值聚合为单台常规同步电机,聚合参数表示如下:
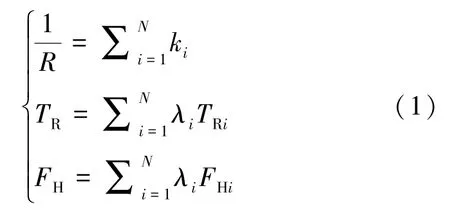
因此,结合式(1)及图1的模型可得常规同步电机参与一次调频的频域表达式为:
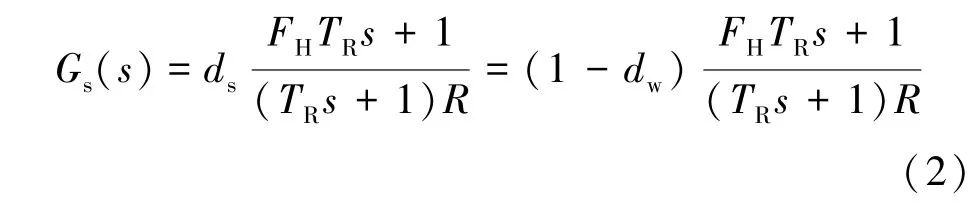
1.1.2 系统惯性响应
由于电力系统频率具有时空分布特性,在频率波动过程中各节点频率表现为围绕惯性中心的频率波动,因此,通常使用系统惯性响应的频率来表示系统频率。
如图1所示,其中间部分表示整个电力系统的系统惯性响应,其等值惯性常数Hsys表达式如下:
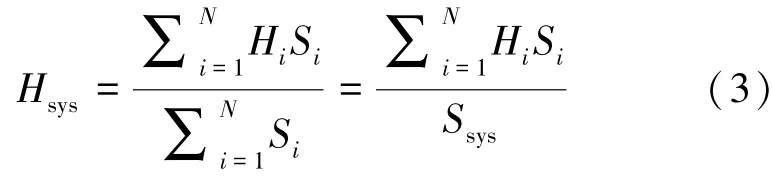
式中,Ssys为系统总装机容量,Hi、Si分别为第i台常规同步电机的惯性常数、额定功率。
1.2 风机线性化模型
为方便研究风机的一次调频能力以及风速波动对电网系统频率的影响,提出反映图1下半部分的风机线性化模型,如图2所示。模型输入为频率波动(Δf)与风速波动(ΔVw),输出为风能波动(ΔPw)。
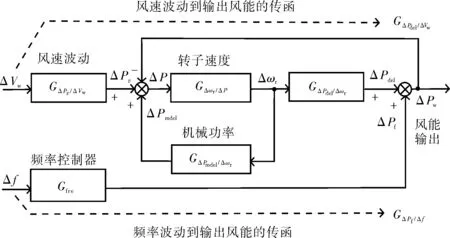
图2 风机线性化模型
在图2中,其主要表现为风速波动到输出风能的传递函数GΔPdel/ΔVw以及频率波动到输出风能的传递函数GΔPf/Δf,分别反映了风速波动及风机一次调频能力对输出风能的影响,以下对其进行详细推导。
风机从风中可获取的机械功率Pm计算如下[18]:
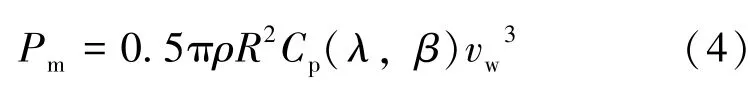
式中,ρ、vw和R分别是空气密度、风速和叶片长度。风机风能利用系数Cp是叶尖速比λ的非线性函数,为获取最大风能,叶片桨距角β通常设置为0,于是Cp可以表示为λ的二阶多项式:
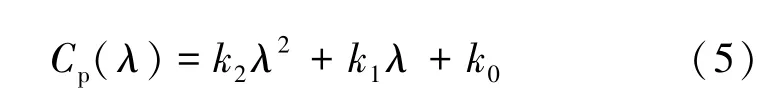
式中,k2、k1和k0为常数系数,λ=Rωm/vw,ωm为机械转速,在恒定风速下,维持最佳叶尖速比λopt=-k1/2k2,可获得的最大机械功率为:
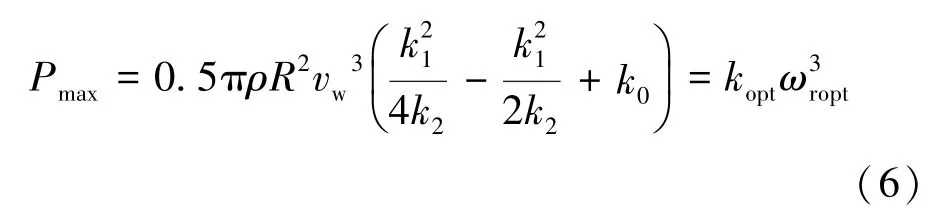
但是为了参与一次调频,风机需放弃捕获最大风能,维持减载运行以提前预留备用容量,选取超速控制为风机预留备用容量,对式(6)乘以一个减载比系数kdel,得减载的有功功率为:

此外,风速波动可以通过将线性化的风能扰动量添加到捕获的机械功率中得到,表示如下:

由上式及所提模型可知,随着风电接入比例dw的提高,风速波动引起的风能波动也随之增大,加大了系统频率波动,而由于风机一次调频与风速显然没有直接耦合关系,因此可得风机一次调频对风速波动引起的频率波动调节能力有限的结论。
2 基于虚拟滤波器的风机一次调频控制方法
由风机线性化模型分析可知,传统风机一次调频控制方法对风速波动引起的频率波动没有有效的调节措施,无法在风速波动的情况下为电网提供较好的频率支撑。因此,为提高风电的最大接入比例,通过文献[19]所提的虚拟滤波器控制技术,结合传统风机一次调频控制技术,提出一种基于虚拟滤波器的风机一次调频控制方法。
2.1 虚拟滤波器控制原理
虚拟滤波器控制原理如图3所示,通过在功率控制环节引入一个附加的虚拟滤波器,使整个机组的传递函数与在风机输出端附加一个传统滤波器的传递函数相同,进而将虚拟滤波器与传统滤波器进行等效的替换。
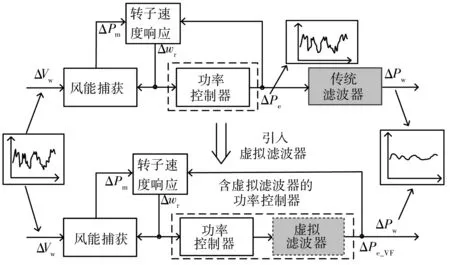
图3 虚拟滤波器原理图
通过等效替换,虚拟滤波器不仅能够实现滤波效果进而抑制风速波动引起的频率波动,还能减少额外的滤波器投资和维护成本。
2.2 考虑风机一次调频的虚拟滤波器设计
基于上述虚拟滤波器控制原理,以下将对其进行虚拟滤波器设计。其中值得注意的是,若按照上述方法假设传统滤波在风机输出端,则会连同频率控制器输出的调节功率一并滤除,减弱风机一次调频能力。因此,为得到能够有效滤除风速波动所引起的频率波动以及不影响风机一次调频能力的虚拟滤波器,所假设的传统滤波器应加装在如图4所示的位置,即功率控制器输出之后,频率控制器输出之前。
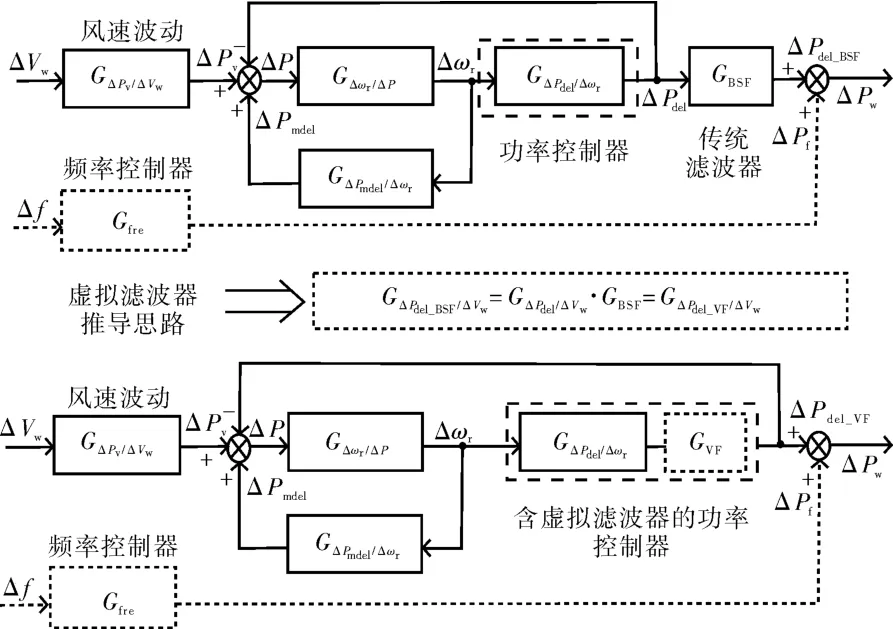
图4 考虑风机一次调频的虚拟滤波器推导图
首先,为避免过多的风能损失,传统滤波器应设计为二阶带阻滤波器,其传递函数可表示为:
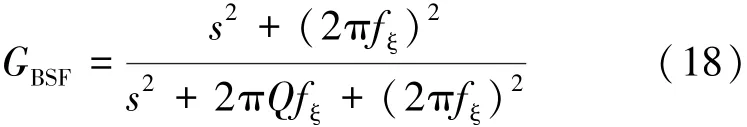
式中,Q为品质因数,一般设计为0.9;fξ为阻带中心频率。为了实现最好的滤波效果,提高风电的最大接入比例,fξ可设计为风速波动频率分量的最大值,其表达式如下:
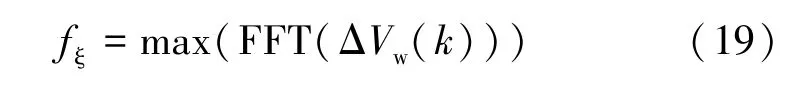
然后,假设在功率控制器后放置了一个带阻滤波器,其整体的风机传递函数如图4上半部分所示,可以得到从风速到由传统滤波器滤波后输出功率的传递函数为:
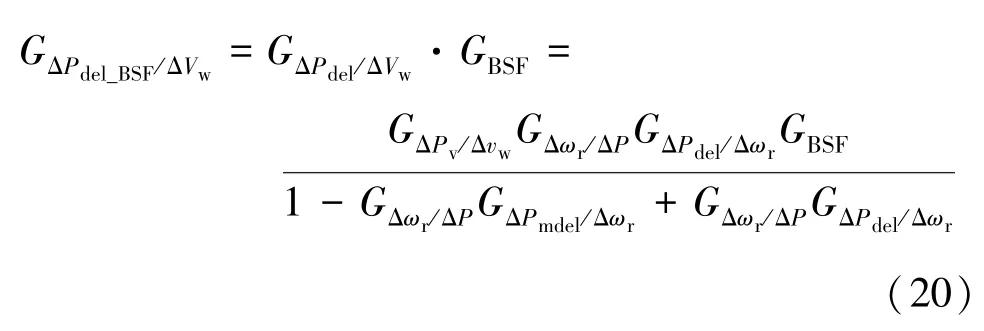
其次,假设在风机功率控制器内引入虚拟滤波器,其整体的风机传递函数如图4下半部分所示,可以得到从风速到由虚拟滤波器滤波后输出功率的传递函数为:
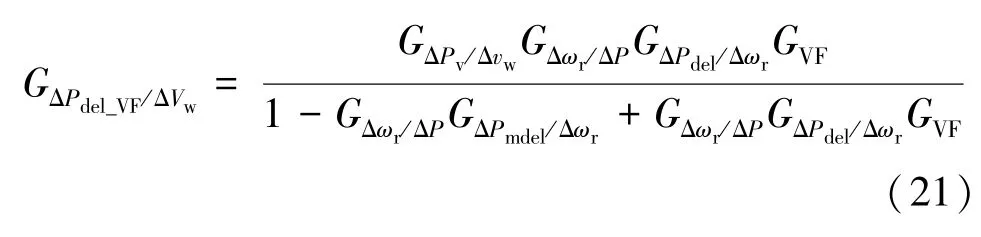
最后,再通过将式(20)、(21)相等的方式,求得虚拟滤波器传递函数的表达式为:
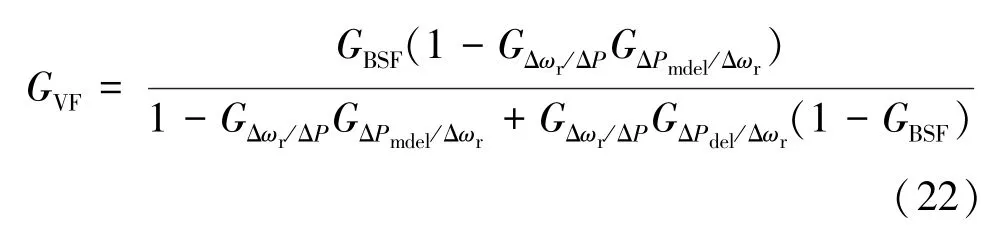
式中,GΔPmdel/Δωr、GΔPdel/Δωr为常数,GΔωr/ΔP、GBSF分别为一阶及二阶传递函数,因此虚拟滤波器为容易求得的三阶传递函数。值得注意的是,实际的风机控制器为数字处理器,若要运用于实际风机中还需要对其进行离散化,再运用数字滤波器控制技术使之适用于数字处理器。
3 计及风速波动和频率约束的风电最大接入比例计算方法
为衡量所提出的提高风电最大接入比例控制方法的效果,提出计及风速波动和频率约束的风电最大接入比例计算方法,以此准确量化提高的风电接入比例。
首先,根据图1建立的含风机参与一次调频的电力系统频率响应模型可得:
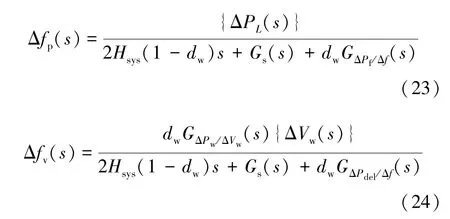
式(23)为当风速波动等于0时,由负荷波动引起系统频率波动的频域表达式;式(24)为当负荷波动等于0时,由风速波动引起系统频率波动的频域表达式。
本计算方法选用能够反应系统抵御有功扰动能力的稳态频率偏差为约束条件。中国国家标准《电能质量 电力系统频率偏差》规定稳态频率偏差需在±0.2 Hz以内[20],得约束表达式为:

式中,q为该表达式的最高次数,mi、ni(i=0,1,…,q)为含风电接入比例dw的常数。
基于式(27),采用差分方程得N个风速波动序列ΔVw(k)引起的N个频率偏差序列Δfv(k)。
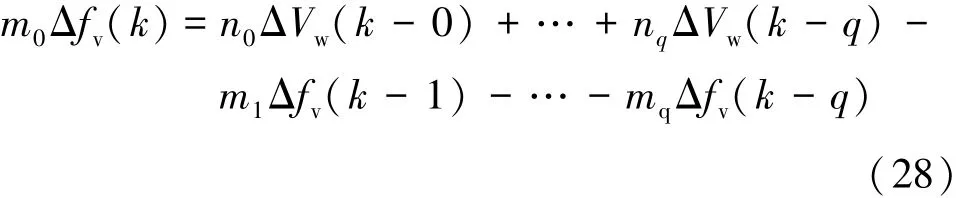
式中,k为离散序列号。当序列k=kmin,k=kmax时为N个频率偏差序列Δfv(k)的最低点Δfv_min与最高点Δfv_max,并且由于其参数mi、ni为仅含有dw为未知数,因此可表示为:
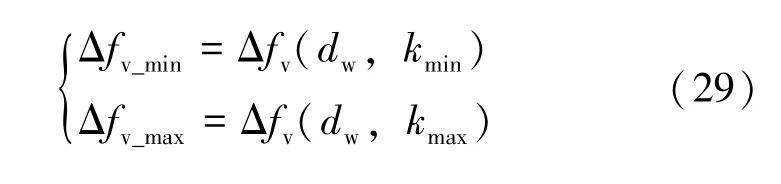
最后,把式(26)、 (29)带入稳态频率约束条件式(25),得:
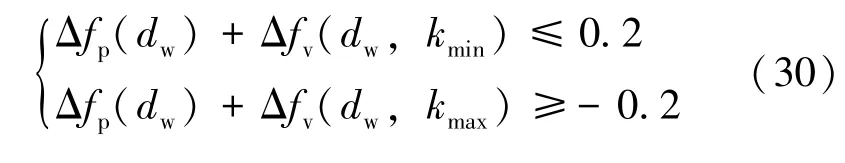
在式(30)中,仅含dw为未知数,根据约束条件可得最大的风电接入比例dw_max。
4 仿真验证
在Matlab/Simulink上搭建如图5所示的含风机的IEEE9节点时域模型,母线9接入由若干双馈感应风力发电机等值聚合的风电场。
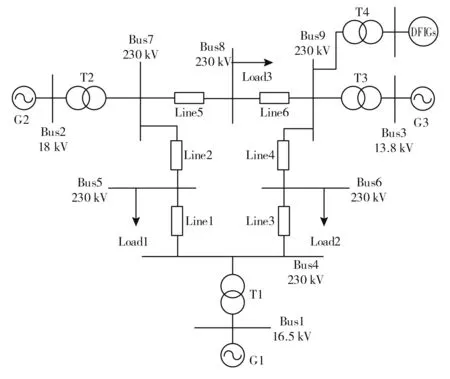
图5 仿真系统图
其中,IEEE9节点系统总装机容量Ssys为500 MV·A,总负荷为450 MW,各同步发电机蒸汽涡轮调速器参数见表1,各同步发电机参数见表2。
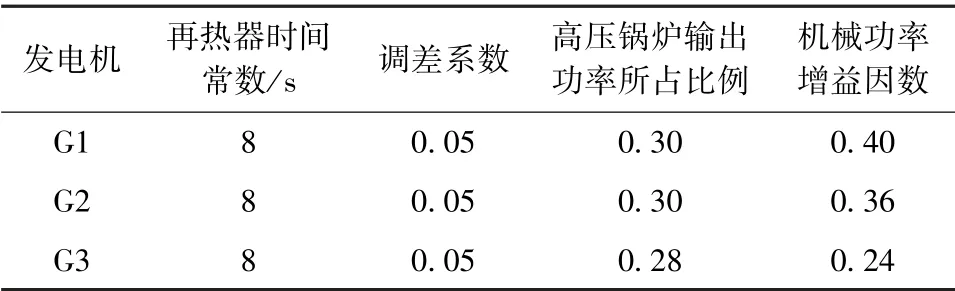
表1 蒸汽涡轮调速器参数
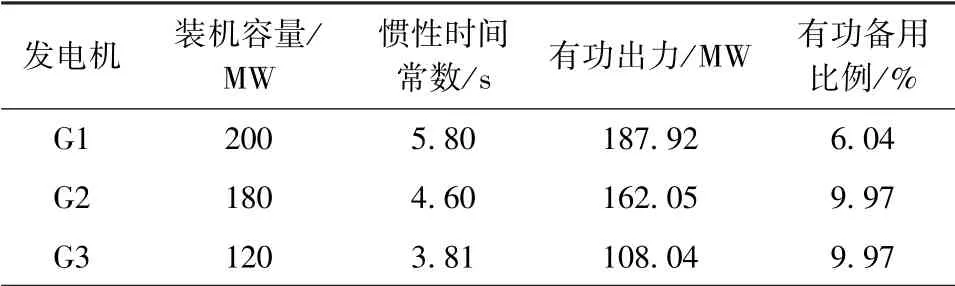
表2 IEEE9节点系统发电机参数
风电场由单台1.5 MW的双馈感应风力发电机等值聚合,风机惯性时间常数Hw为5 s,阻尼系数Dw为0.006,Cp系数k2、k1、k0分别为-0.037 65、0.428 9、-0.761 3,减载系数kdel为0.9,一次调频系数Rw为0.05。
4.1 模型验证
为验证所提模型的准确性,设风电接入比例dw为15%,即风电场容量为70 MW;在100 s之前不考虑风速波动的影响;在100 s时负荷突增总容量的5%,即25 MW;在120 s频率重新达到稳态时考虑风速波动的影响。风机运行情况对比图如图6所示,系统频率波动对比如图7所示。
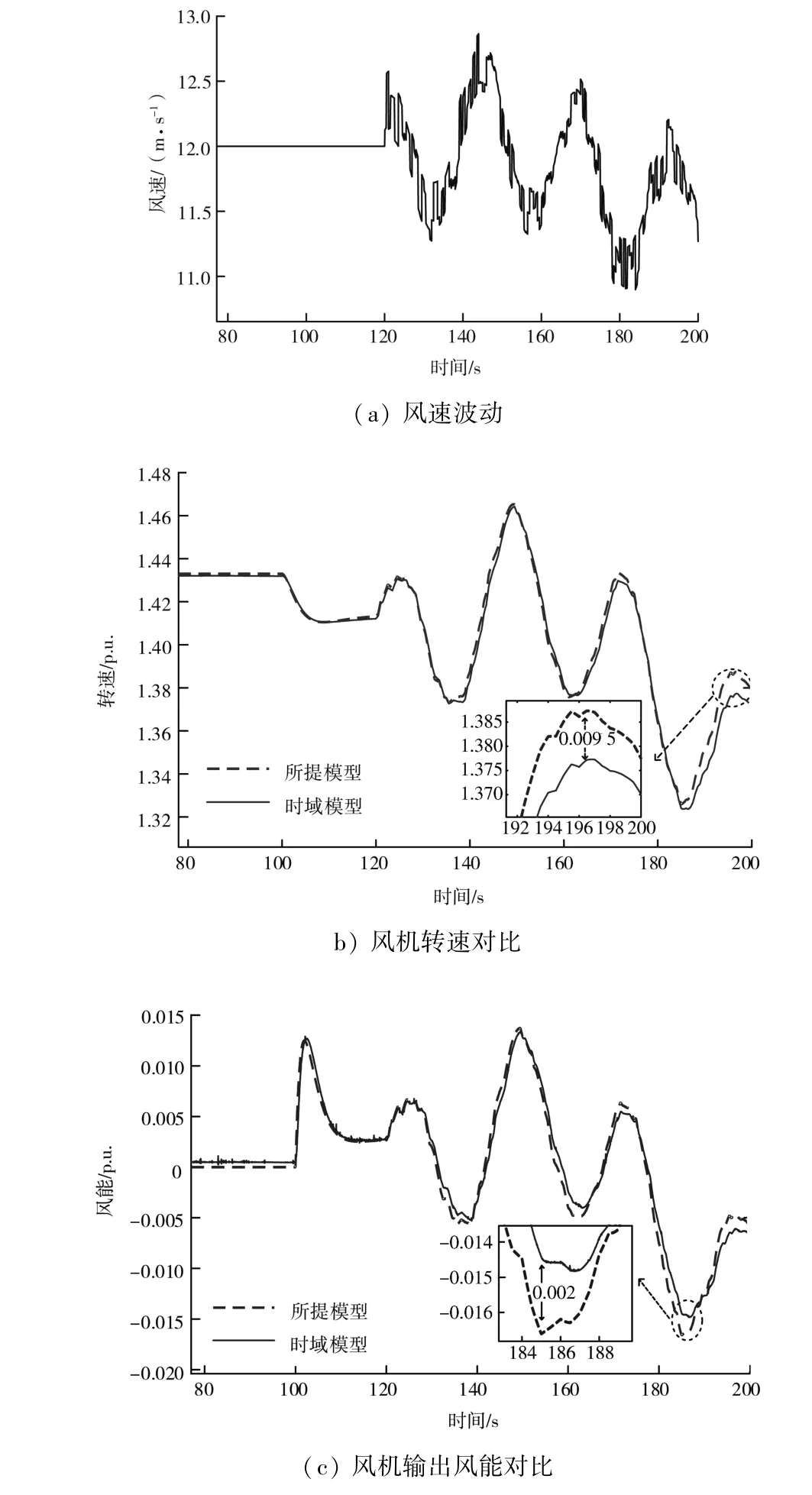
图6 风机运行情况对比图
由图6(b)风机转速对比图可看出,所提模型的风机转速与时域模型仅相差0.009 5 p.u.;由图6(c)风机输出风能对比图可看出,所提模型的风机输出风能与时域模型仅相差0.002 p.u.;由图7系统频率波动对比图可看出,所提模型的系统频率波动与时域模型仅相差0.007 2 Hz,误差较小,验证了所提模型的准确性。
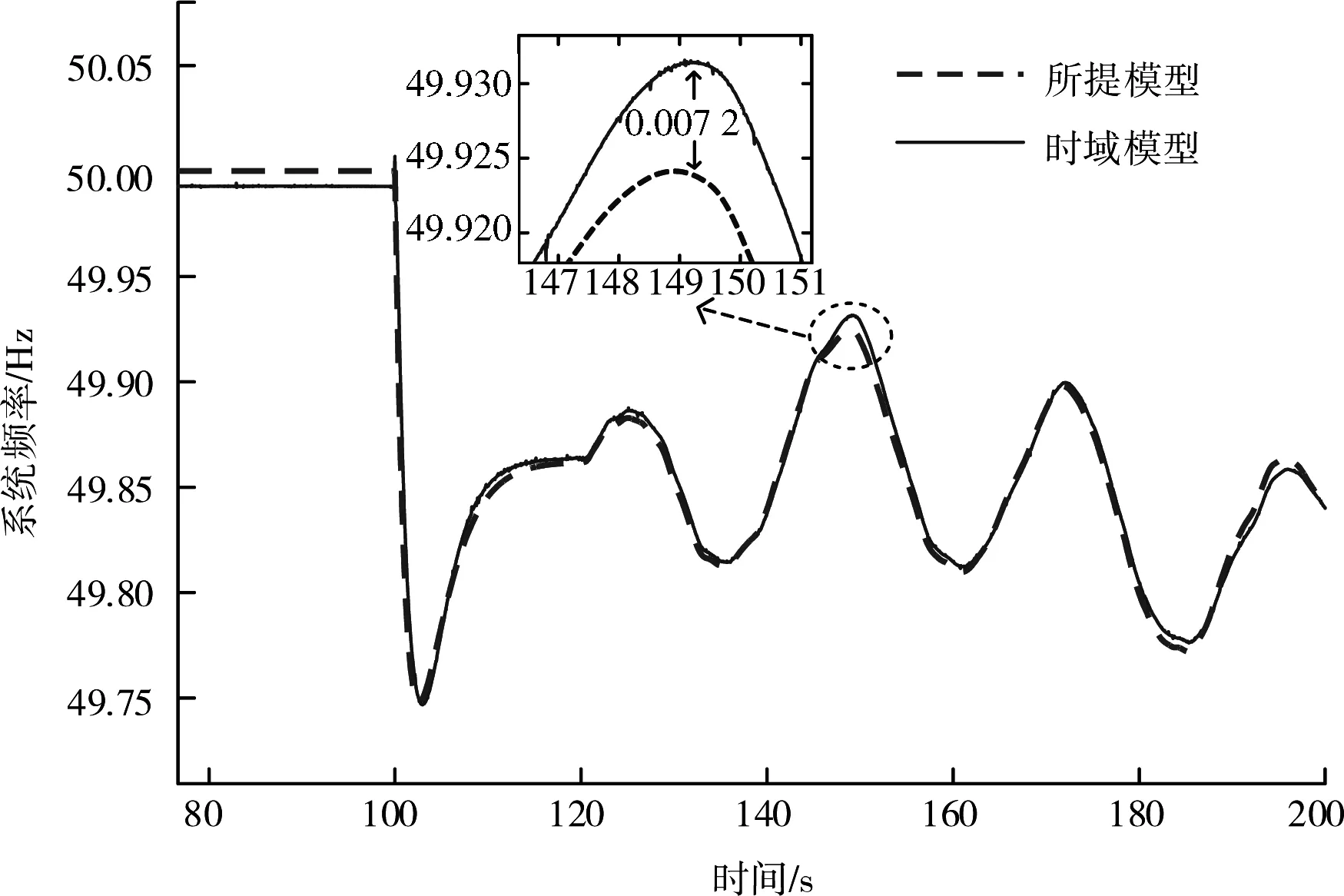
图7 系统频率波动对比图
4.2 计算方法验证
为验证所提计算方法的准确性,仿真场景与模型验证部分相同,设置的不同负荷波动水平为4%、5%、6%,风机一次调频系数为0.05,按所提计算方法设置风电接入比例为15.35%、11.30%、7.31%,仿真波形如图8所示。设置不同风机一次调频系数为0.02、0.04、0.06,负荷波动水平为5%,按所提计算方法设置风电接入比例为14.90%、11.66%、10.95%,仿真波形如图9所示。
由图8不同负荷波动水平下的系统频率波动图可以看出,随着负荷波动水平的提高,频率曲线整体往下移动,接近频率约束极限值0.2 Hz,风电接入比例下降较明显,并且从图中可以看出,受风速波动影响后的系统稳态频率最低点与频率约束极限值分别相差0.000 9 Hz、-0.002 4 Hz、-0.006 0 Hz,与频率约束极限值的误差在3%以内,验证了在不同负荷波动水平下的所提计算方法的正确性。
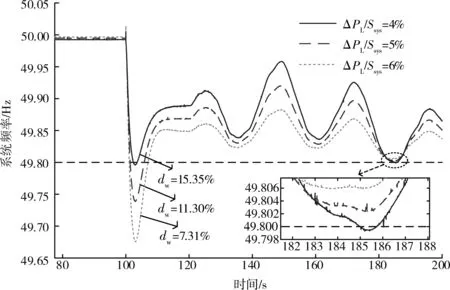
图8 不同负荷波动水平下的系统频率波动
由图9不同风机一次调频系数下的系统频率波动图可以看出,随着一次调频系数的升高,系统调频能力下降,导致风电接入比例随之下降,并且从图中可以看出,受风速波动影响后的稳态频率最低点与频率约束极限值分别相差-0.004 3 Hz、-0.003 8 Hz、-0.003 5 Hz,与频率约束极限值的误差在2%以内,验证了在不同风机一次调频系数下的所提计算方法的正确性。
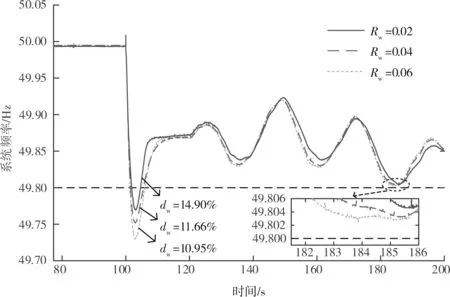
图9 不同风机一次调频系数下的系统频率波动
4.3 控制方法验证
为验证所提控制方法的有效性,仿真场景与计算方法验证部分负荷波动水平为5%时相同,在风机功率控制模块中引入虚拟滤波器,阻带中心频率fξ设为0.05 Hz,按所提计算方法设置风电接入比例为15.08%,系统频率波动如图10所示。
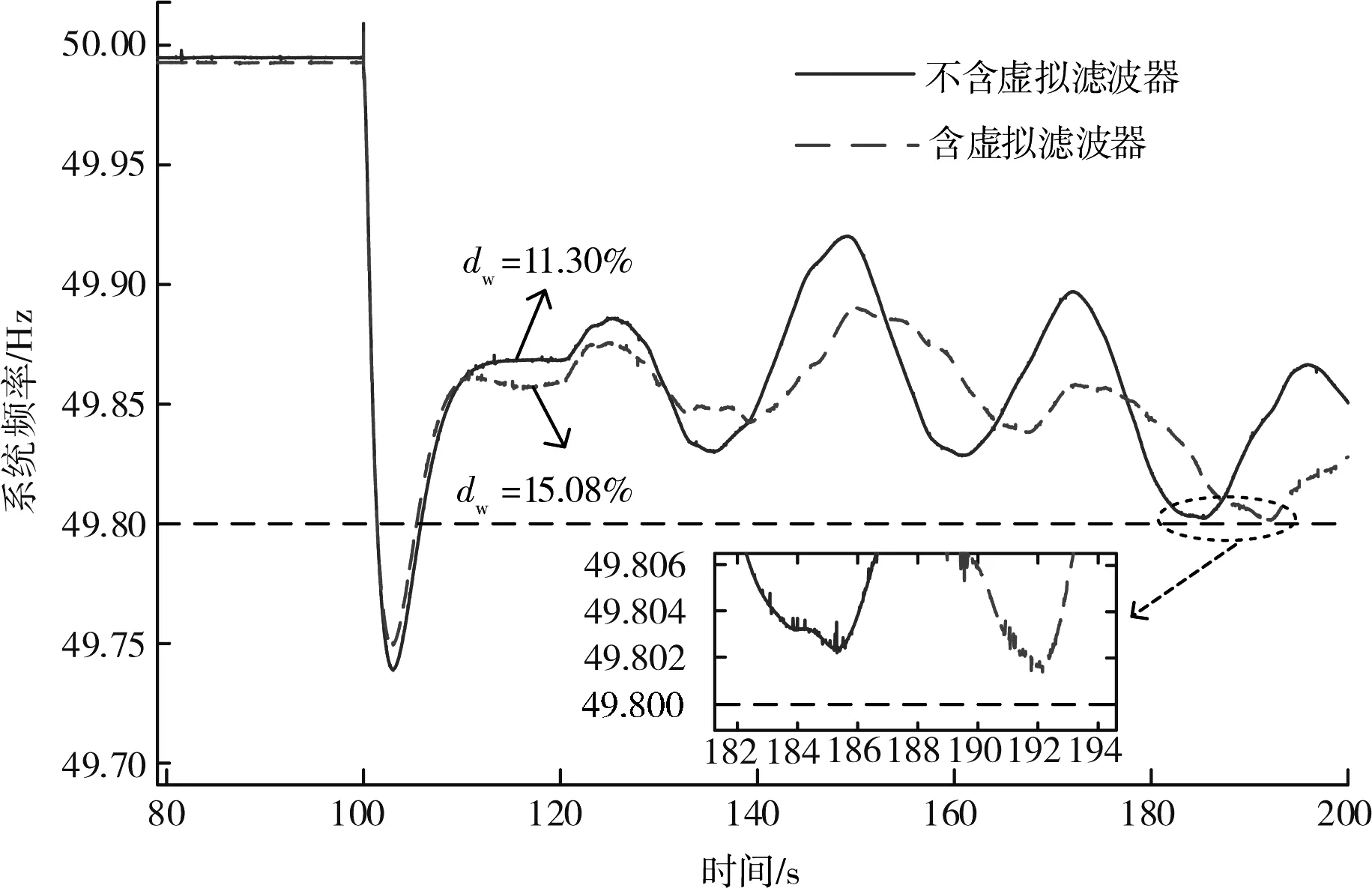
图10 引入虚拟滤波器的系统频率波动
由图10引入虚拟滤波器的系统频率波动图可以看出,系统频率波动有明显改善,并且当风电接入比例为15.08%时,稳态频率最低点与频率约束极限值仅相差不到0.001 Hz,误差在0.5%以内。与不含虚拟滤波器相比,风电最大接入比例提高了3.78%,验证了所提控制方法的有效性。
此外,为验证阻带中心频率fξ参数选取的正确性,即风速波动频率分量的最大值,充分利用虚拟滤波器,实现风电最大接入比例。其中,风速波动频率分量的最大值由图11(a)风速FFT分析图所示,其值为0.042 Hz,按所提计算方法计算不同阻带中心频率的风电最大接入比例结果如图11(b)所示。可以看出,当阻带中心频率为风速波动频率分量的最大值时,风电最大接入比例为17.96%,与不加虚拟滤波器的11.30%相比,风电接入比例最大提高了6.66%,验证了阻带中心频率参数选取的正确性。
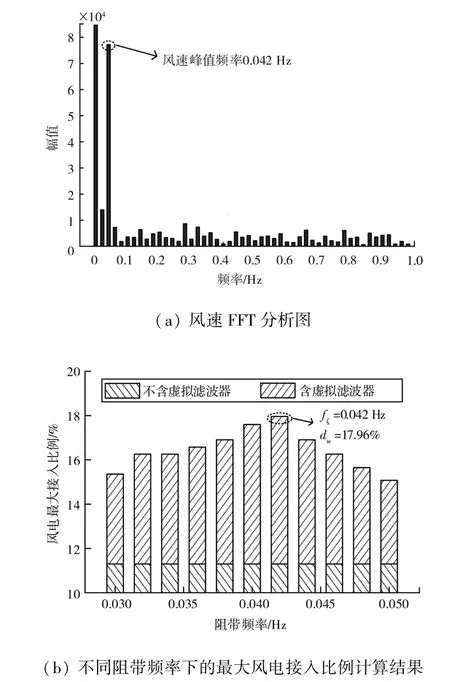
图11 阻带频率验证图
5 结论
随着风电接入比例不断提高,电网系统惯性水平下降,风速波动对电力系统的影响也随之加强,频率问题突出,成为制约风电接入比例进一步提高的约束条件,降低了风电消纳能力。因此对计及风速波动和频率约束的风电最大接入比例进行研究,所得结论如下:
1)在以系统稳态频率偏差为约束的情况下,影响风电最大接入比例的主要因素为负荷变化水平及风机一次调频系数,并且风电最大接入比例随着负荷变化水平及风机一次调频系数的增大而减少,其中负荷变化水平影响最大。
2)在Matlab/Simulink上进行仿真验证的结果表明,所提计算方法在不同负荷波动水平下与频率约束极限值的误差在3%以内,在不同风机一次调频系数下与频率约束极限值的误差在2%以内;并且所提控制方法能够较明显地提高风电最大接入比例。
3)若不考虑风速波动对风电最大接入比例的影响,而对风机电源进行规划,则结果偏向乐观。因此,所提计算方法对于指导风电电源规划和维持系统频率安全稳定运行具有十分重要的意义。

