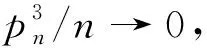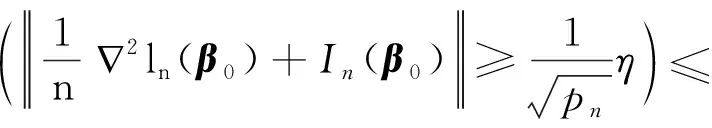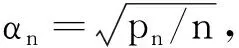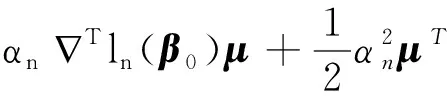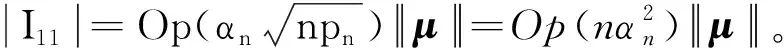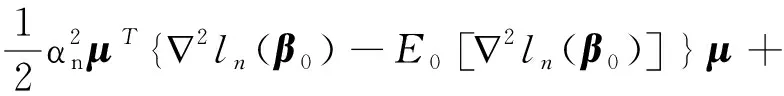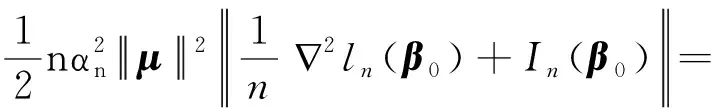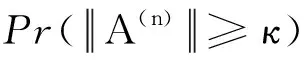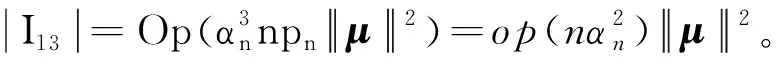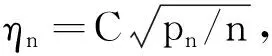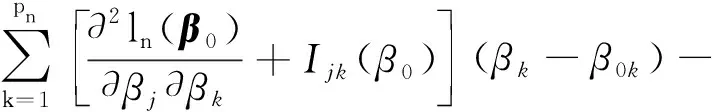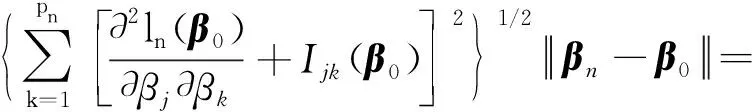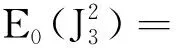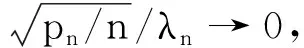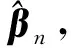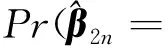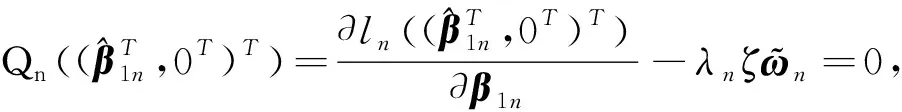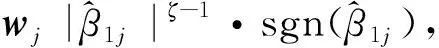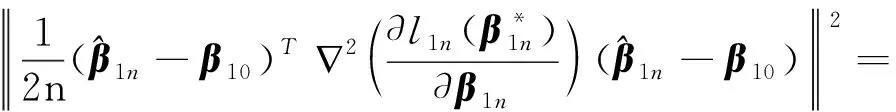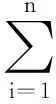高维数据下广义线性模型自适应桥惩罚估计的变量选择
夏亚峰,何 佳
(兰州理工大学理学院,甘肃 兰州 730050)
在对变量选择问题的研究中,应用较为广泛的是基于惩罚函数的估计方法,它可以同时实现模型的参数估计和变量选择,常见的惩罚函数有平滑剪裁绝对偏差函数(SCAD,smoothly clipped absolute deviation)、Bridge、Lasso等[1-3]。文献[4]中对高维数据变量选择问题进行了系统研究;文献[5]中研究了高维线性模型下SCAD估计的渐近性质;在高维部分线性模型下,文献[6]中结合样条方法和Dantzig或Lasso变量选择方法,同时实现变量选择和参数估计;文献[7]中研究了参数个数有限时Bridge估计的渐近性质;文献[8]中又将此结果拓展到参数无穷维情形;文献[9]在桥估计的基础上,使用自适应桥估计去研究高维线性模型的变量选择问题;文献[10-11]中基于众数回归对部分线性可加模型提出一种变量选择方法,并基于众数回归下自适应Bridge方法研究了高维数据下部分线性可加模型的变量选择问题;针对广义线性模型的参数估计和变量选择问题,文献[12]中研究了高维广义线性模型中非凹惩罚似然估计的渐近性质;文献[13]中研究了广义线性模型中参数发散时Bridge估计的Oracle性质;文献[14]中利用SCAD方法研究广义线性模型下删失数据的变量选择问题,并证明了SCAD方法的相合性和Oracle性质;文献[15]中利用L1惩罚方法,同时实现变量选择和压缩;文献[16]中利用惩罚的拟似然SCAD方法,研究高维广义线性模型的参数估计和变量选择问题。
受上述文献启发,将自适应桥估计方法利用到广义线性模型中并考虑维数pn随着样本量n的增加而增加并逐渐趋于无穷大的高维数据,研究了广义线性模型的参数估计和变量选择问题。利用对数似然函数和自适应桥方法构造惩罚估计目标函数,证明了高维数据下自适应桥估计能相合地识别出非零参数,实现变量选择,并证明了变量选择方法具有Oracle性质,利用数值模拟和实例分析验证所用方法在有限样本下的优良性。
1 变量选择
考虑广义线性模型
(1)
其中:Y为响应变量;v(·)的逆函数为已知的光滑连接函数;βn∈Θn为pn维未知参数向量;X为pn维随机协变量;ε是均值为0的随机误差项,维数pn随着n的变化而变化。假设误差项ε的分布函数为F(·),密度函数为f(·),假设其一阶和二阶函数存在,δ=1表示误差项绝对值小于Δ=1×10-3,δ=0表示误差项绝对值大于Δ。随机变量W=(δ,X,Y),其对数似然函数为


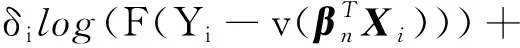
研究给出进行变量选择的惩罚似然函数
(2)
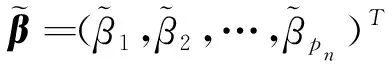

2 变量选择的渐近性质
为证明方便,文中先给出一些简化表示。
令
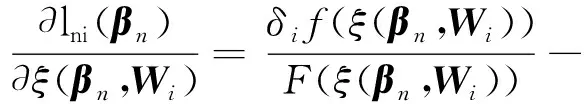


d2(βn,Wi)XijXikXil。
设W的分布为Pβn,E0为关于Pβ0的期望,正则条件为:
(B2) 对j,k=1,…,pn,有
-E0[d1(β0,W1)X1jX1k]。
(B3) Fisher信息阵

令In(β0)最小和最大特征根为λmin{In(β0)}和λmax{In(β0)},N1、N2为给定的常数,有
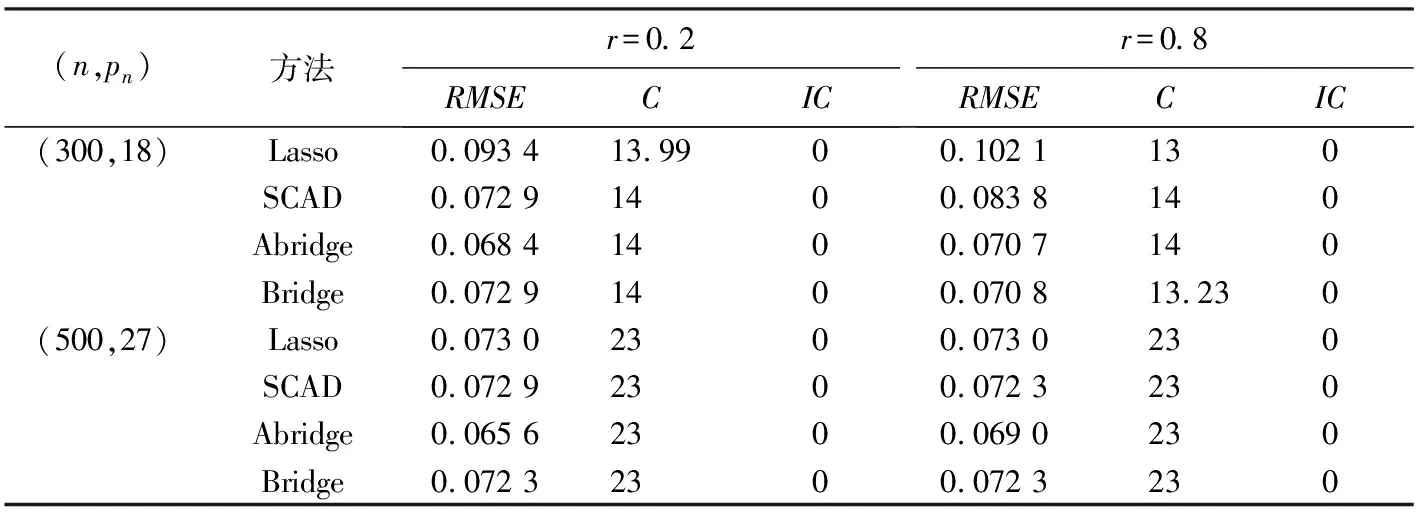
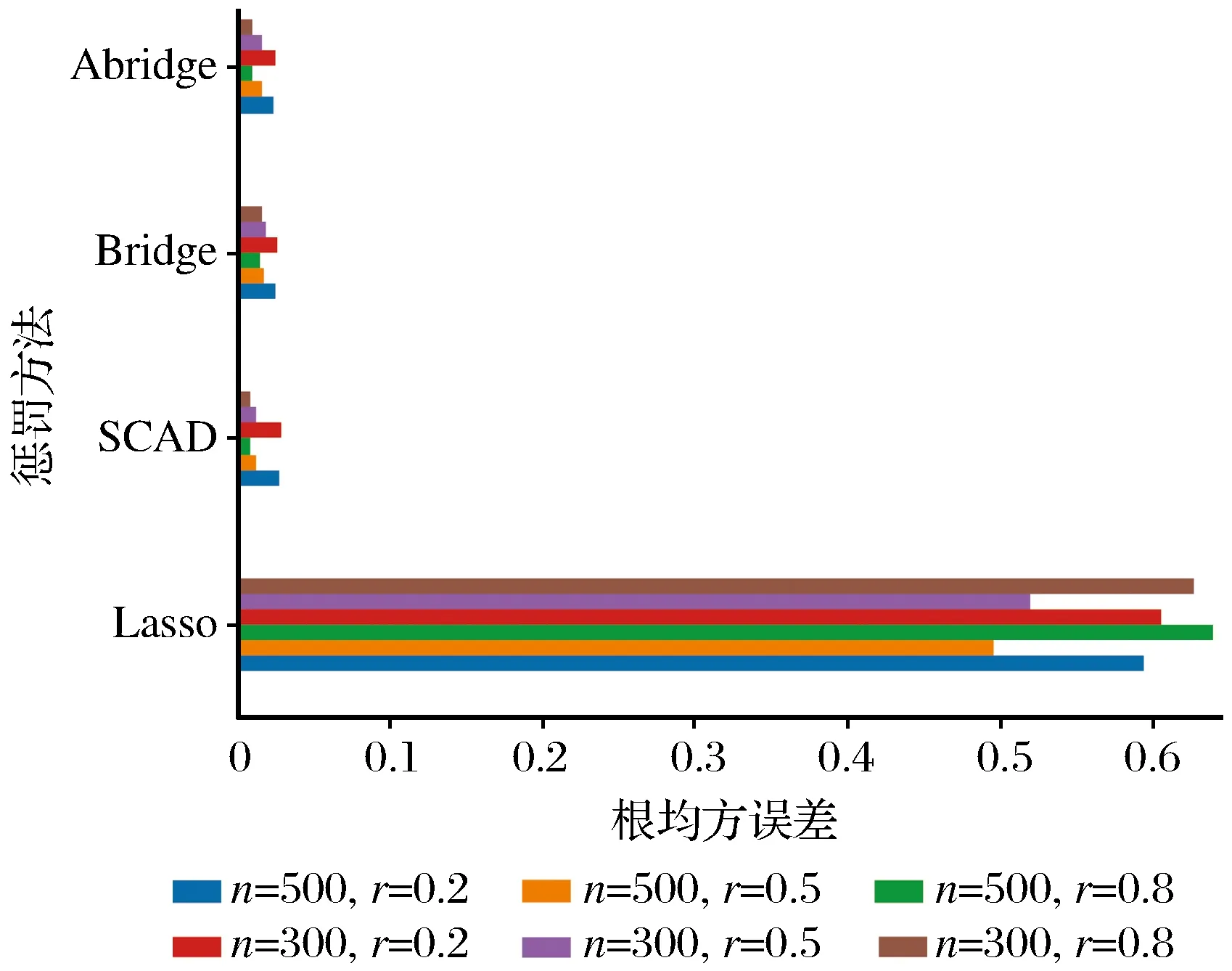
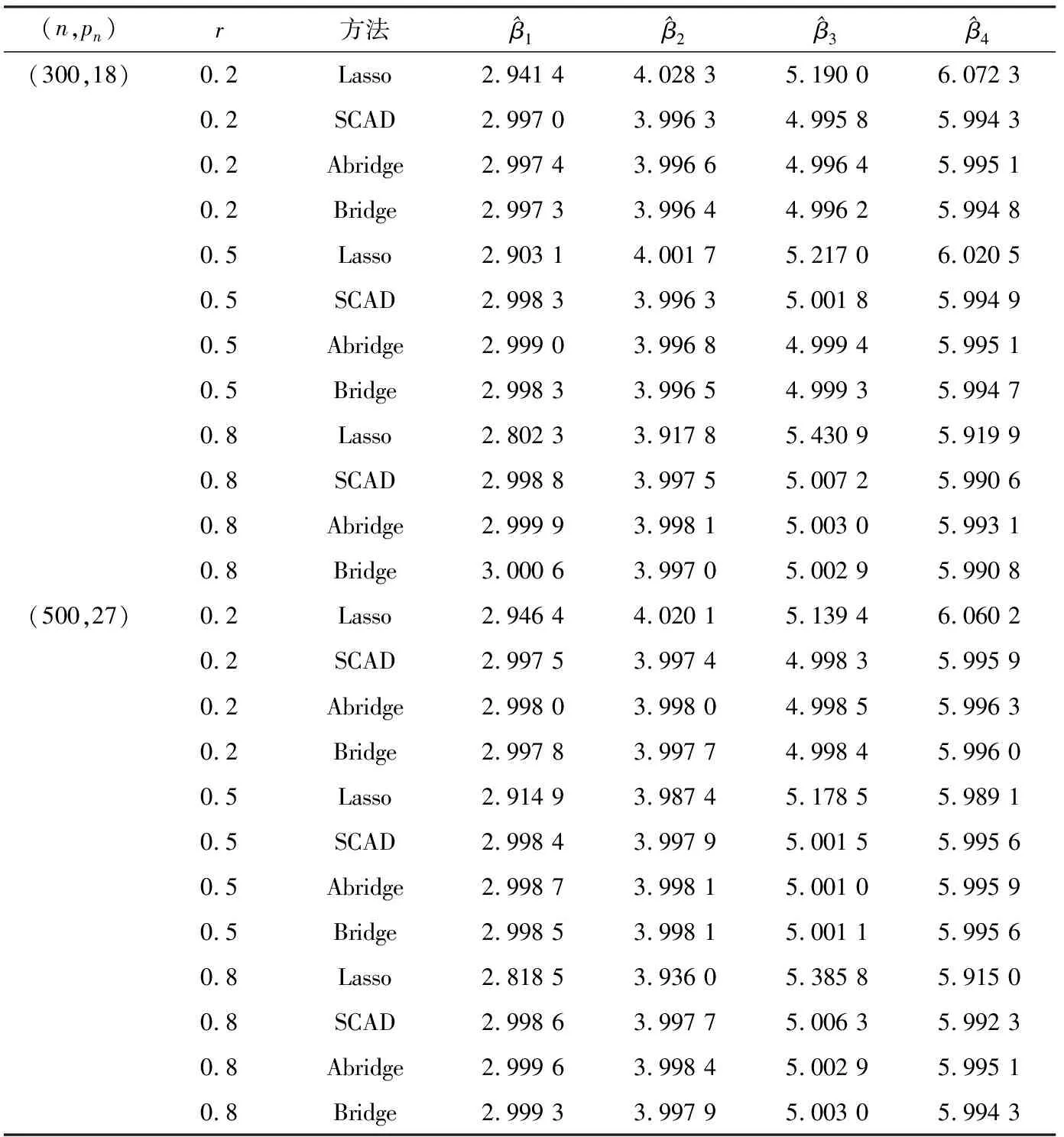
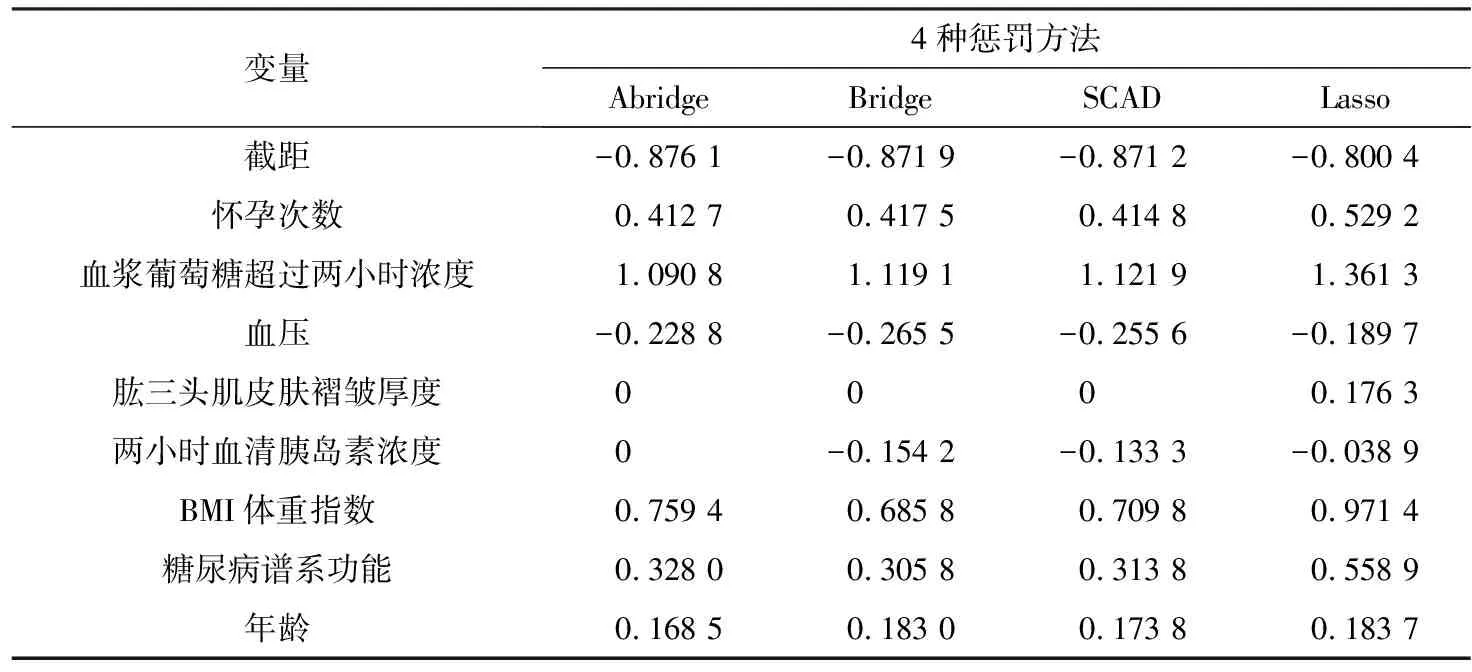
0 N2<∞。 (B4) 若存在正数N3,N4,N5使得max1≤j≤pn|X1j|≤N3,E0[d1(β0,W1)]2≤N4,并且 (B5) 假设存在一个足够大的开集Sn⊆Θn,对所有的βn∈Sn,存在函数M(Wi)满足|d2(βn,Wi)|≤M(Wi),i=1,…,n,除此之外,存在常数N6使得E0M2(W1)≤N6。 (B7) 假设wjλn=O(1),并且存在常数0 b0≤min{|β1j|,1≤j≤kn}≤max{|β1j|,1≤j≤kn}≤b1。 (1) 稀疏性: (2) 渐近正态性: 3.1 算法和惩罚参数的选择 研究使用局部二次逼近算法给出桥估计,并且讨论调整参数λn的选择问题,ζ的取值和文献[10]中一样,取ζ=0.5。 [Pλn(|βj|)]′=P′λn(|βj|)sgn(βj)≈ (3) 其中 例1 (Logistic回归模型) 利用Python生成100组数据,每组数据含有n个样本,每个样本均来自Logistic回归模型: 其中:β为pn维参数向量,令β1=2,β2=3,β3=4,β4=5,其余分量皆为0;协变量X服从pn维多元正态分布,其均值为0;协方差矩阵第(i,j)个元素为r|i-j|,r分别取0.2和0.8。模拟采用2种不同的样本量,一种是n=300,pn=18;另一种是n=500,pn=27。 为了比较不同方法的差异,研究给出了3个评价模型好坏的指标,其中RMSE表示根均方误差,其表达式为 μ(βTX)=E(Y|X)的期望是关于观测值(X,Y)。Logistic模型的模拟结果见表1,表1中分别列出了自适应桥估计(ζ=0.5)、桥估计(ζ=0.5)、Lasso估计以及SCAD估计,C表示模拟中零系数被正确估计为0的平均个数;IC表示非零系数被错误估计为0的平均个数。 表1 Logistic模型的模拟结果 由表1可知,这4种方法都能较好地选择出非零系数,并且随着样本量的增加,不同方法对应的根均方误差减小,并都能更好地选择出真实的模型,但自适应桥估计根均方误差最小,变量选择效果最好。 例2 (Poisson回归模型)研究模拟100组数据,每组数据含有n个样本,每一个样本均来自Poisson回归模型: E(Y|X)=exp(βTX), 其中:β1=3,β2=4,β3=5,β4=6,βj=0(j=5,…,pn);协变量X生成方式为Xi1=sin(2Ui)+ei1,Xi2=(0.5+Ui)-2+ei2,Xi3=log(3Ui+8)+ei3,Xi4=exp(Ui)+ei4,Xij=eij,j=5,…,pn。 r取3种不同的值:0.2,0.5,0.8;n、pn分别取2组值n=300,pn=18和n=500,pn=27,并分别给出了自适应桥估计、桥估计、SCAD估计以及Lasso估计的比较结果(见表2)。 由表2可知,4种方法βj(j=1,2,3,4)的估计都接近真实值,并且随着样本量的增加,其估计都能够逼近参数真实值,其中估计效果由好到坏依次为Abridge、Bridge、SCAD、Lasso。图1表示了4种不同的方法在r、n取不同值时根均方误差的横向条形图。由图1可知,随着样本量的增加,4种方法根均方误差都呈现出下降趋势,其中Lasso方法的误差最大,自适应桥估计的误差最小。因此,自适应桥估计变量选择效果最好。 图1 不同惩罚方法的根均方误差Fig.1 Root mean square error of different penalty methods 表2 系数估计的比较结果Table 2 Comparison results of coefficient estimates 以下根据国家糖尿病与消化和肾脏疾病研究所提供的768条皮马印第安人糖尿病数据,使用Logistic回归模型研究患者的血压、体重指数、年龄等因素与是否患糖尿病的关系,响应变量y:y=0表示患糖尿病,y=1表示不患糖尿病;考虑8个协变量,x1为怀孕的次数,为数值型变量,x2为口服葡萄糖耐量试验中血浆葡萄糖超过两小时的浓度,x3为血压,x4为肱三头肌皮肤褶皱厚度,x5为两小时血清胰岛素浓度,x6为BMI体重指数,x7为糖尿病谱系功能(根据家族史评估糖尿病可能性的功能),x8为年龄。研究对Abridge、Bridge、SCAD和Lasso 4种惩罚估计进行了比较,调整参数通过BIC准则进行选择,分别取0.48、0.22、0.025、0.08。 4种惩罚方法的变量选择结果见表3,由表3可知,Lasso没有剔除变量,SCAD和Bridge都剔除了1个变量,而自适应桥估计剔除了2个变量,选择的模型最简单,说明自适应桥估计能更好地选择出重要的变量。 表3 不同方法的变量选择结果 证明任意η>0,由Chebyshev不等式可得 定理1的证明首先证明对任意的η>0,存在充分大的常数C满足 (4) Qn(β0+αnμ)-Qn(β0)=ln(β0+αnμ)-ln(β0)- I1+I2。 利用Taylor展开式,把I1展开可得 I11+I12+I13, 对于I11,由条件(B1)和(B3)得 I12为 对于I121,由引理1得 对于I13,记 E0(M(Wi)XijXik)]2≤ 在条件(B6)下,有 对于I2,根据(B7),有 当C足够大时,I122起主要作用,又因它的符号为负,所以式(4)成立,定理1证毕。 对任意常数C,以概率1有 以概率1有 由Taylor展开 因此 (5) 对于 其中:Ijk(β0)为矩阵In(β0)第j行k列的元素, 同时 可得 (6) 对于J3,由条件(B6)得 因此 (7) 根据式(5)~式(7),有 把似然函数的一阶导数Taylor展开得 即 因为 又因为 所以 对任意kn维向量α,有 令 则E0(Vni)=0, 验证Lindeberg-Feller中心极限定理的条件,对任意η>0, 由Hölder不等式,有 根据条件(B3)和(B4)得 且 因此 由Lindeberg-Feller中心极限定理和Slutsky定理,定理2(2)成立。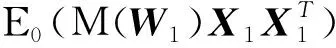
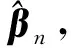

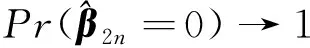
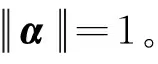
3 数值模拟和实例分析


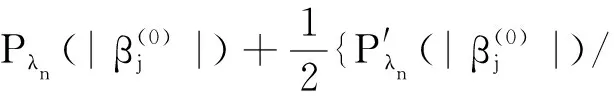



3.2 数值模拟
3.3 实例分析
4 定理的证明