基于对抗性策略的变分自编码模型

陈亚瑞，王浩楠，张芝慧，杨剑宁，丁文强

(天津科技大学人工智能学院，天津300457)

生成模型(generative model)是通过引入隐变量建模数据的生成过程，训练后的模型可以用于生成新的数据样本．深度生成模型是生成模型和深度神经网络相结合．变分自编码(variational autoencoder，VAE)模型[1-2]和生成对抗网络(generative adversarial networks，GAN)[3-4]作为应用最广泛的两类深度生成模型，近年来凭借强大的性能表现受到图像处理[5]、计算机视觉、自然语言处理等[6]领域的关注．这两类深度生成模型能对复杂的高维度数据进行建模，而且随着它们变体模型的产生[7-8]，已经在数据特征提取、数据降维、目标检测和生成新数据集等方面取得较好的实际效果．变分自编码模型通过对生成过程进行显式建模，采用似然函数为优化目标，其中基于变分推理的证据下界优化度量指标为衡量模型优劣提供了定量指标，该模型已经成为深度生成模型领域的研究热点．

变分自编码器模型作为无监督特征学习[9]的重要工具，其主要思想是通过神经网络对生成模型和后验概率分布的变分近似分布进行建模，通过学习隐空间与数据空间的特征映射，输出新的重构数据空间．但因其推理模型表示能力不足，所以生成图像较为模糊，生成样本多样性受限．当前很多研究工作基于变分自编码模型进行改进，提升数据生成质量及生成数据的多样性．Manuel等[10]将类别标签信息加入到变分自编码模型中，提出条件变分自编码(condition variational autoencoder，CVAE)模型，并将其应用于半监督学习中．Louizos等[11]为了让变分自编码模型能够更明确地学习到某些非变性因素的特征表示，提出变分公平自编码(variational fair autoencoder，VFAE)模型．Vincent等[12]为了去除生成图像的噪点，改善变分自编码的生成效果，提出了去噪变分自编码(denoising variational autoencoder，DVAE)模型．Kingma等[13]将自回归神经网络(如PixelRNN[14])应用于变分自编码模型中，充分利用自回归神经网络的生成能力，极大地提升了变分自编码模型的生成效果．

生成对抗网络[3-4]的提出受到业界的广泛关注．因其采用对抗训练的方式，能够生成更清晰、更真实的数据样本，进而被应用于无监督和半监督学习领域[4,15]．然而，生成对抗网络存在训练不稳定、梯度消失和模式崩溃等问题有待解决．为了优化变分自编码模型和生成对抗网络，有许多研究人员将生成对抗网络的对抗策略引入到变分自编码模型中.Makhzani等[7]将对抗策略引入到自编码模型中，提出对抗自编码(adversarial autoencoder，AAE)模型，其度量模型精度的方式已不再是变分下界，虽然没有广泛沿用，但模型思想具有很高的研究价值．Larsen等[16]将生成对抗网络引入到自编码模型中，提出一种优化像素级图像的混合模型(AE-GAN)．Dumoulin等[17]提出对抗学习推断理论(adversarially learned inference)，将对抗策略引入到推理模型中，让对抗策略与变分自编码模型的结合进一步成为可能．Mescheder等[8]将对抗思想引入到变分贝叶斯模型中，用“黑盒方法”重新定义推理模型，提出对抗变分贝叶斯(adversarial variational Bayes，AVB)模型．Huang等[18]提出Intro变分自编码(introspective variaitonal autoencoders，Intro VAE)模型，并通过该模型得到了超高分辨率的图像生成效果．

在变分自编码模型及其变体模型中，推理模型的表示能力不足一直是生成图像效果不佳的重要原因.因此，本文提出基于对抗策略的变分自编码(adversarial variational autoencoder，AVAE)模型解决这一问题．首先介绍变分自编码模型和对抗变分贝叶斯模型，其次对提出的基于对抗策略的变分自编码模型进行详细介绍，最后结合实验验证该生成模型在给定参数的情况下能够增加推理模型的表示能力，得到更好的变分似然下界，有效提升图像的生成效果．

1 背 景

1.1 变分自编码模型

传统变分自编码模型是由推理模型(又称编码器)和生成模型(又称解码器)组成的[1-2]，其中，推理模型是通过多层神经网络将真实数据x编码为一个低维隐变量z，生成模型是将隐变量z通过多层神经网络还原映射到高维度数据空间．变分自编码模型结构如图1所示，其中白色节点z表示隐变量，灰色节点x表示可观测量，节点之间的有向线段表示变量之间的依赖关系；黑色实心小方块表示模型参数值；qφ(zx)与虚线部分为推理过程，pθ(zx)与实线部分为生成过程，φ和θ为相关过程的参数；方框表示该过程可以重复出现，例如在该模型中基于隐变量可以重复生成数据样本，观测到N条数据，则该过程重复出现了N次．

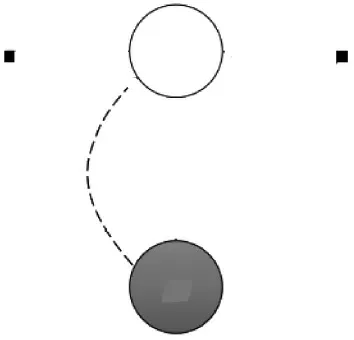
图1 变分自编码模型Fig. 1 Variational autoencoder model

在变分自编码模型中，先验概率分布 p(z)服从标准高斯分布 N (0,I)，推理模型通过引入近似后验概率分布qφ(zx)逼近真实后验概率分布pθ(zx)，φ和θ均为模型参数．通过推导，得到数据对数似然logpq(x)的下界，又称为证据下界[2]或变分似然下界，即

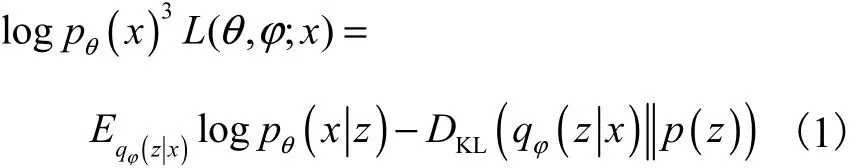
其中：Eqφ(zx)logpθ(xz )为生成模型的重构误差项，用来比较新生成的图像与真实图像之间的差距，通过最大化重构误差项，模型可以得到更好的生成效果；

DKL(qφ(zx) p(z ))为两个分布之间的KL散度，用DKL进行正则化约束，通过让近似后验概率分布逼近给定的先验分布，使正则化项最小．

此时，变分自编码模型的目标是通过随机梯度下降算法[19]学习到最优的模型参数φ和θ，使得证据下界最大，即

变分自编码模型在训练过程中使用了重参化方法(reparameterization)[1-2]，目的是解决随机梯度下降过程中参数的梯度消失问题．

作为生成模型，虽然变分自编码模型将变分下界作为模型精度度量标准，但是在图像生成过程中仍存在生成图像模糊和生成样本多样性受限等问题．这些问题与近似推理模型的表示能力有限有关[16,18]，而对抗变分贝叶斯模型很大程度上解决了这一问题．

1.2 对抗变分贝叶斯模型

对抗变分贝叶斯模型[8]通过引入“黑盒方法”增加推理模型的表示能力，然后引入对抗策略求解目标函数中的正则化项．该模型主要包含3个组件，分别是推理模型、生成模型及鉴别器，如图2所示：Qφ为推理模型，将真实图像x通过神经网络编码为隐变量z；Pθ为生成模型，将隐变量z还原映射到高维度数据空间；D为鉴别器，用于鉴别隐变量与图像数据形成的数据组合；φ和θ为相关组件的学习参数．

图2 对抗变分贝叶斯模型结构示意图Fig. 2 Schematic diagram of the structure of adversarial variational Bayes model

对抗变分贝叶斯模型将先验概率分布 p(z)设定为标准高斯分布 N (0,I)，将真实图像x产生的隐变量z输入到生成模型中，得到重构图像x′并计算负重构误差．在此期间，对抗变分贝叶斯模型重新定义优化为

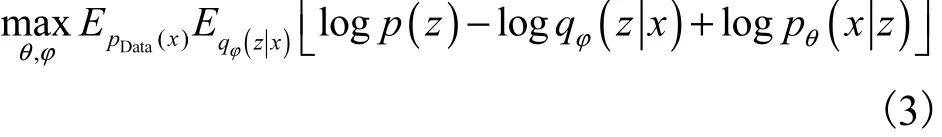
并通过“黑盒方法”向推理模型中加入随机噪声，增加推理模型的灵活性，能有效地表示任何种类隐变量的分布，进而将式(3)中 log p(z)-log qφ(zx )与鉴别器建立联系，将其推导成含有鉴别器函数 D(x,z)的形式，得出优化参数φ时的最优解为

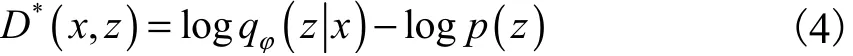
至此，对抗变分贝叶斯模型的目标函数为

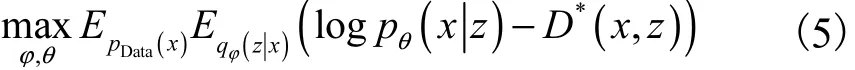
模型的鉴别器有两个输入，分别是真实图像与隐变量组合(x1,z1)和真实图像与先验随机变量组合(x2,z2)．变分贝叶斯模型认定(x1,z1)为正样本，(x2,z2)为负样本，以此让模型引入对抗的训练方式．鉴别器的目标函数为

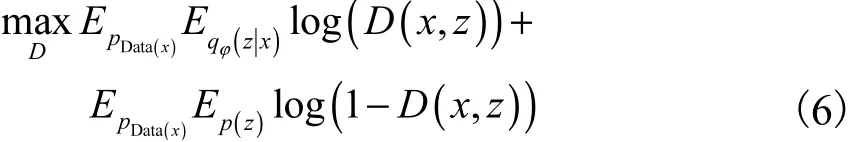
对抗变分贝叶斯模型在训练过程中让推理模型和鉴别器交替训练，持续提升推理模型的表示能力和生成模型的生成能力．待模型训练完成后，可以将先验分布采样的随机噪声通过生成模型直接映射到数据空间，以此作为模型的最终输出．该模型生成图像的效果相比于变分自编码模型有很大提升，且随着训练的进行，生成的图像也更具多样性．

2 改进的变分自编码模型

2.1 引入噪声的推理模型

在传统变分自编码模型的推理模型中引入随机噪声，将推理模型表示成qφ(zx,ε1)，其中ε1是来自标准高斯分布 N (0,I)的随机噪声，φ为推理模型参数．具体做法是将低维度的随机噪声加入到高维度的图像数据中，增加推理模型输入端的维度．此时推理模型中不仅包含图像数据，而且包含低维的随机噪声，可提升其表示能力．VAE和AVAE推理模型示意图如图3所示，其中Q为推理模型，x为图像数据，z为隐变量，1ε为来自标准高斯分布的随机噪声，即推理模型噪声．模型的优化目标为

图3 VAE和AVAE推理模型示意图Fig. 3 Schematic diagram of VAE and AVAE inference model

其中：φ和θ分别为推理模型和生成模型的参数.AVAE模型通过在推理模型中引入随机噪声，使其获得学习更复杂数据分布的能力，进而提升推理模型的表示能力．

AVAE模型沿用变分自编码模型中的重参化方法[2,11]避免模型在训练过程中遇到参数的梯度消失，进而能更顺利地使用随机梯度下降对参数更新．模型重参化过程如图4所示，其中x为图像数据，z为隐变量，μ和σ为推理模型的神经网络计算出的隐变量分布的均值和方差，ε2为来自标准高斯分布的重参化噪声，gφ为重参化函数，其形式为 gφ(ε, x )=

图4 AVAE模型的重参化及推理过程Fig. 4 Reparameterization and inference process of AVAE model

重参化方法是对于每一个隐变量z ～ qφ(zx,ε1)，通过使用随机变量ε2的可微分函数 gφ(ε2,x )重新设定隐变量z

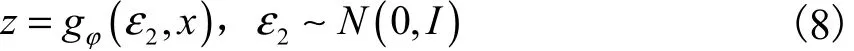
对于每一个真实数据x，采用随机梯度下降算法，将式(7)改写为

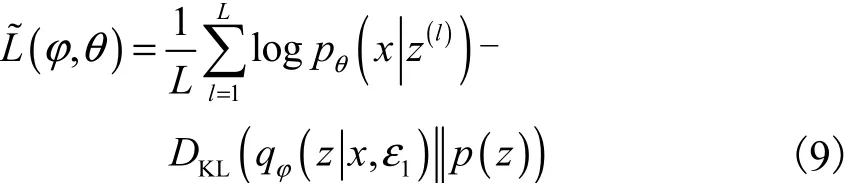
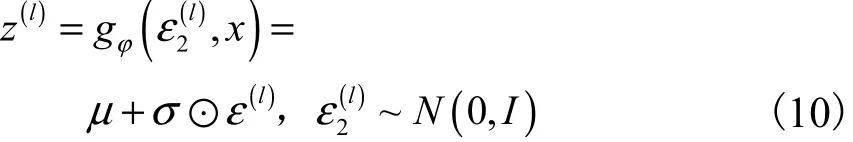
将样本 z(l)输入到式(9)中等号后边第二项，即推导出生成模型生成真实数据x的概率密度．基于随机噪声的模型优化问题为

2.2 对抗网络

AVAE模型通过增加对抗网络引入对抗策略，同时增加聚合正则化约束，进而更好地训练推理模型．推理模型qφ(zx )表示单个样本x的近似后验概率分布，对于样本集的隐变量空间可以用聚合后验概率分布 q(z)表示，即

AVAE模型在对抗网络的输入中加入图像数据x，如图5所示，其中Dφ为对抗网络部分，z为隐变量，z′为从先验分布 p(z)中采样的随机变量．对抗网络将图像数据与先验随机变量的组合(x,z′)判定为正样本，将图像数据与隐变量的组合(x,z)判定为负样本．

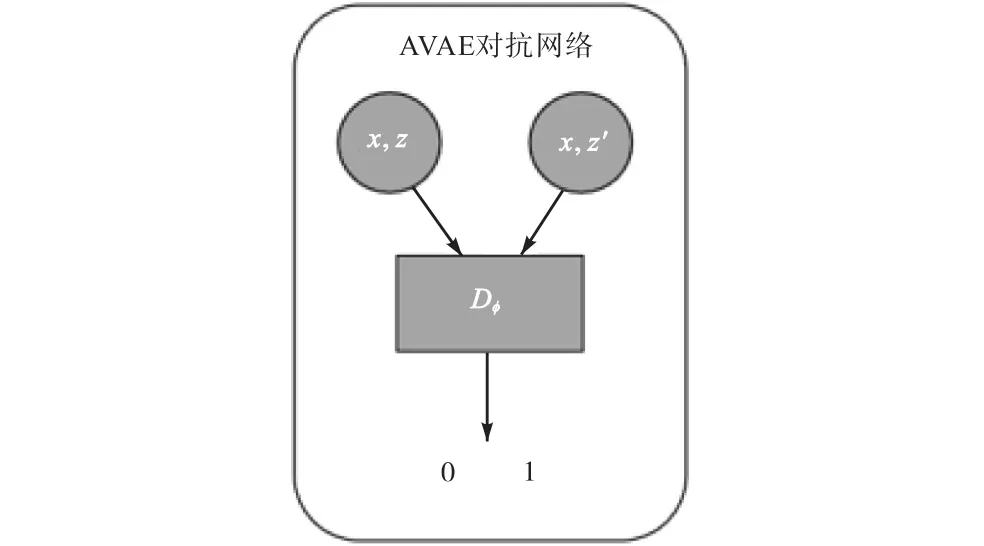
图5 AVAE模型对抗网络示意图Fig. 5 Schematic diagram of AVAE model’s adversarial network

由此，对抗网络的目标函数为

其中：Dφ(x,z)为对抗网络函数，φ表示对抗网络参数．对抗网络的目的是增加聚合正则化项，让聚合后验分布q(z)近似给定的先验分布p(z)．因为增加了聚合正则化约束，模型可以通过对抗训练进一步优化推理模型参数φ．对抗网络在模型下的优化问题为

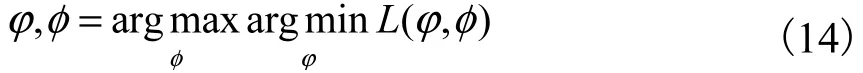
2.3 AVAE算法

AVAE模型通过向变分自编码模型的推理模型增加随机噪声，增加推理模型的表示能力，同时，引入对抗网络增加聚合正则化约束进一步训练推理模型．模型给定先验分布p(z)和随机噪声ε1的分布均为标准高斯分布 N (0,I)，推理模型为qφ(zx,ε1)，生成模型为pθ(xz)，使用重参化方法及随机梯度下降算法对参数进行更新．

模型先将图像数据x和随机噪声ε1同时输入到推理模型中，增加推理模型的输入维度，提升其表示能力．在训练过程中，推理模型优化式(11)和对抗网络优化式(14)交替进行优化．训练分两个阶段，通过式(11)计算并优化推理模型的参数φ，以最大程度让聚合后验概率分布 q(z)近似给定的先验分布 p(z)；通过式(14)，先计算并优化对抗网络参数φ，让对抗网络与推理模型进行对抗训练，接着再一次更新推理模型参数φ，完成聚合正则化约束，增加推理模型的表示能力．

在训练过程中，生成模型参数θ通过式(11)不断得到优化．待模型训练完成后，可以直接通过对p(z)分布随机采样作为隐变量，并借助训练好的生成模型生成更真实、更清晰的新图像数据．AVAE模型算法如下：

1. i←0.

2. WHILE没有收敛DO.

3. 从真实数据分布pData(x)采样

5. 从先验分布p(z)中采样{ z(1), z(2),… ,z(k)}.6. 对于优化式(11)计算参数的随机梯度.

7. 基于随机梯度下降算法，可以得到参数的更新式θ←θ+ higθ，φ←φ+ higφ.

8. 对于优化式(14)计算参数的随机梯度.

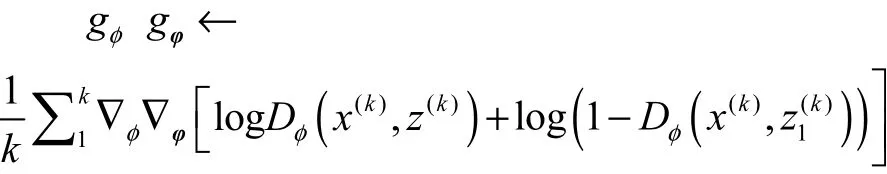
9. 基于随机梯度下降算法，可以得到参数的更新式φ←φ+ higφ，φ←φ+ higφ.

10. i←i+1.

11. END WHILE.

3 实 验

3.1 实验设计

本节所用的数据集包括手写数字数据集MNIST(数据来源：http://yann.lecun.com/exdb/mnist/)和服饰商品数据集Fashion-MNIST(数据来源：http://www.worldlink.com.cn/en/osdir/fashion-mnist.html)两种．MNIST数据集包括手写数字图像0～9，共10类数据，其中训练图像60000张，测试图像10000张．这些手写数字图像都经过尺寸标准化，固定大小为28像素×28像素，每个像素值为0～1，每个图像都被平展并转换为784(28×28)个特征的一维numpy数组．Fashion-MNIST数据集包括T-shirt(T恤)、pullover(套衫)、dress(裙子)、coat(外套)、sandal(凉鞋)等服饰商品，共10类数据，其中训练图像60000张，测试图像10000张．这些服饰图像也经过尺寸标准化，图像固定大小为28像素×28像素．实验在tensorflow 1.15环境下进行，操作系统Windows10，运行平台工具Python3.7．

实验中AVAE模型的推理模型、生成模型和对抗网络均采用三隐层全连接神经网络，中间节点个数分别为256、64、32．参数的优化主要采用自适应矩估计(Adam)算法，该算法是随机梯度下降算法的一种变形，可以保证每次迭代参数的学习率具有一定的范围．

3.2 对比实验

3.2.1 随机噪声维度的选择

通过改变推理模型中随机噪声的维度进行实验，衡量标准为模型的变分似然下界(ELBO)．实验中所有模型的隐变量维度均为10，将注入随机噪声的变分自编码模型的噪声维度分别设置为5、10、15．模型在两个数据集上的实验结果如图6所示，其中dim为隐变量维度．根据图6的对比结果可知，向推理模型中注入随机噪声可以提高模型的精度，即得到更优的变分似然下界．同时，随机噪声维度不宜设置过大，其维度为10时在两个数据集上均得到了更好的实验结果．

图6 VAE与注入噪声的VAE模型实验结果Fig. 6 Experimental results of VAE and injected noise VAE

3.2.2 精度对比

通过实验对比VAE模型、加入随机噪声的VAE模型、AVB模型及AVAE模型几种模型的精度，实验的衡量标准为模型的变分似然下界(ELBO)．由于随机噪声维度为10时实验结果较好，所以设置所有模型的随机噪声维度均为10，只改变AVAE模型的隐变量维度为10和15．模型在两个数据集上的实验结果如图7所示，其中dim为隐变量维度．根据图7的对比结果可知，AVAE模型在两个数据集下均得到了更好的实验结果，即得到了更优的变分似然下界．而且相比于改变随机噪声维度，改变隐变量维度对模型结果影响更为显著．与注入随机噪声的变分自编码模型相比，AVAE模型因为引入对抗策略，得到了更优的变分似然下界；同时，当隐变量维度为10时，模型的精度最高．

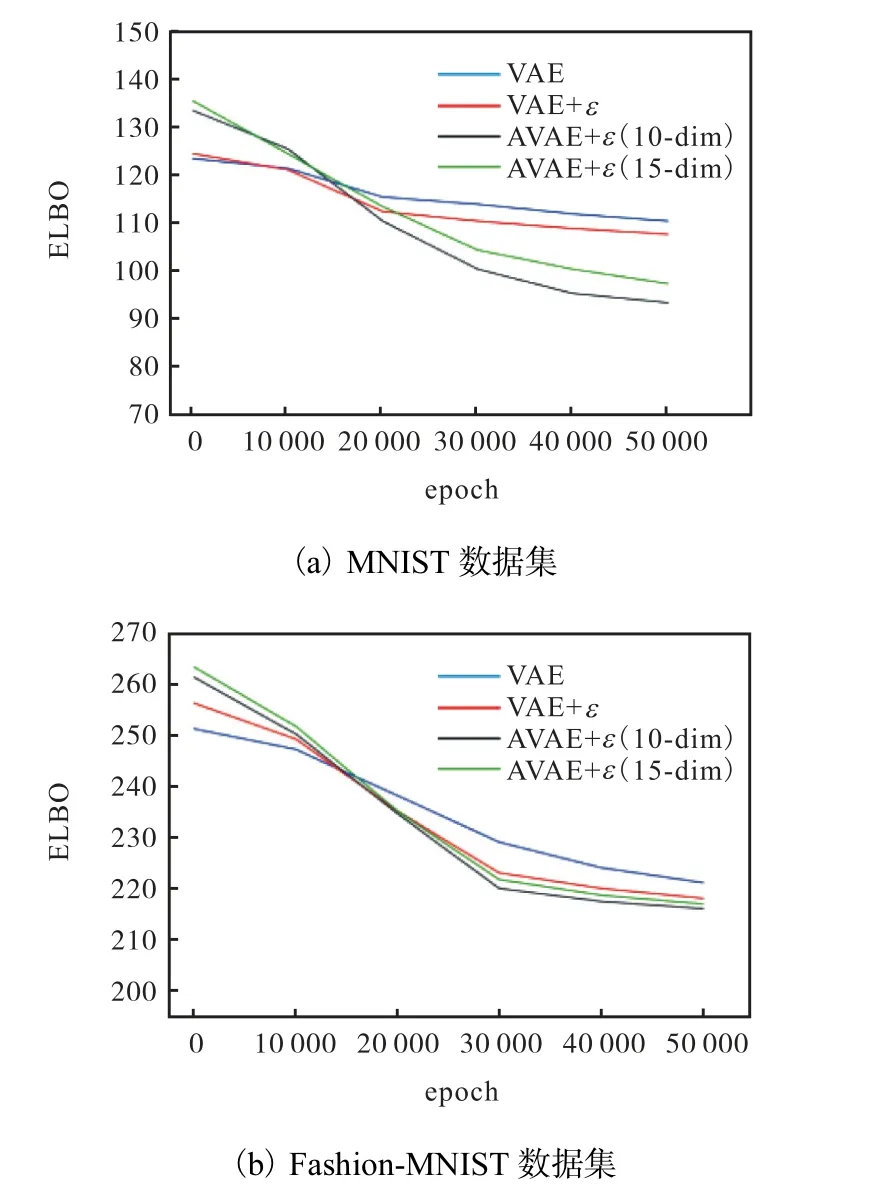
图7 改变隐变量维度AVAE与VAE类模型的实验结果Fig. 7 Experimental results of changing hidden variable dimension in AVAE and VAE models

除此之外，将AVAE模型与对抗变分贝叶斯模型进行对比，在确保网络结构相同的情况下，随机噪声维度均设置为10，并改变隐变量维度．实验结果取多次实验精度的平均值，模型在两个数据集上的实验结果见表1，其中dim为隐变量维度．根据表1的对比结果可以得到，在推理模型中加入随机噪声的变分自编码模型在两个数据集上均可以提升模型精度，且在隐变量维度为10时，得到了更好的实验结果．同时，AVAE模型因为加入对抗网络，比仅加入随机噪声的变分自编码模型在任何隐变量维度上都得到更高的模型精度．通过对比表1的最后两行可以发现，在隐变量为10和15的情况下，AVAE模型在两个数据集上均得到了更好的实验结果，即更优的变分似然下界．随着隐变量维度的增加，推理模型需要学习更多的图像特征，使得每一种模型的精度逐渐变差，且当隐变量维度为10时，AVAE模型在所有模型中得到 的精度最高．

表1 精度对比实验结果Tab. 1 Experiment results of accuracy comparison

3.3 生成图像效果

引入随机噪声的变分自编码模型、变分贝叶斯模型和AVAE模型的隐变量维度和随机噪声维度均为10，生成图像效果如图8所示．相比于引入随机噪声的变分自编码模型，AVAE和对抗变分贝叶斯模型可以生成更加清晰、真实的图像，如图8中的数字“6”和“手提包”．实验结果表明对抗网络和聚合正则化约束的引入可以提高模型的精度，同时提升图像的生成效果．

图8 模型生成图像效果展示Fig. 8 Model generation effect display

4 结 语

本文提出了一种基于对抗策略的变分自编码模型，并在实验中展示其模型精度及生成图像效果．与经典的3种模型的对比实验显示，该模型在给定参数的情况下可以得到优于其他模型的变分似然下界(ELBO)，且在MNIST和Fashion-MNIST数据集上获得了较好的生成图像效果．

经过证实，在推理模型中加入随机噪声可以提高变分自编码模型的模型精度；对抗网络和聚合正则化约束的加入均可以提升推理模型的表示能力．基于对抗策略的变分自编码模型相比于其他模型，可以提高图像生成的效果，且在无监督学习中表现得较为突出．