基于优化模型车辆路径跟踪控制研究

陈 思，韩 愈，唐 超，林 业

(天津科技大学机械工程学院，天津 300222)

自动驾驶是集人工智能、物联网、大数据为一体的新技术，是汽车未来发展的主要趋势之一．路径跟踪是实现自动驾驶的基础，也是实现自动驾驶的核心技术[1]．

路径跟踪就是通过控制车辆的转向使其沿着定义好的路径行驶，近年来它一直是自主地面车辆研究的一个活跃领域．从控制理论的角度出发，路径跟踪的任务可以理解为设计横向控制器不断地生成车辆转向指令来补偿跟踪偏差，从而使车辆可以安全平稳地行驶[2]．

目前，实现路径跟踪的主流方法可以分为两类，基于几何关系设计的几何跟踪法和基于模型控制的方法．几何跟踪法包括Pure Pursuit和Stanley方法等，基于模型控制的方法有MPC、LQR方法等．近年来，国内外学者都在路径跟踪领域进行了大量研究．李红志等[3]提出一种预瞄时间自适应算法，根据不同的预瞄时间，预测将来一段时间内车辆运行情况，并根据优化函数选取合适的预瞄时间使得车辆稳定通过期望路径．明廷友[4]提出一种改进的预瞄跟随算法，确保计算得到的预瞄点落在期望的路径上，避免曲率过大而脱离路径．丁海涛等[5]建立一种形成人-车-路闭环控制的驾驶员模型，引入了横向加速度反馈，并设计一种预览点搜索算法，提高了对路径的包容性．对于路径跟踪问题，尽管模型控制的方法解决这种多约束问题非常有效，同时也展现出了强大的控制性能[6-7]，但算法复杂度较高，优化求解比较费时，在很多情况下几何跟踪的方法更容易被接受．经过不断地改进，几何跟踪的方法已经能够用于路面车辆开发．斯坦福大学为开发的无人车“Stanley”[8]设计了一种新的控制模型(Stanley模型)，成功进行了实车开发并拿下比赛冠军；彭之川等[9]对Pure Pursuit模型进行改进，在客车上实现了路径跟踪．

几何跟踪的方法的优点在于控制模型简单易实现、计算速度快，本文也从模型的几何关系控制原理出发，对比了如今比较流行的控制模型，并提出了优化建议．

1 几何跟踪方法分析

几何跟踪方法就是在建立的车辆道路模型基础上运用几何关系建立前轮转角与车辆位姿和路径点位置的函数关系，给出车辆到达下一个目标点需要的转角控制量．车辆-道路几何模型如图1所示，在大地坐标系下车辆位置参考点为o点，行驶速度为v，下一个目标点为g点，通过车辆-道路几何关系确定此时车辆需要向右转动φ角度，向目标点行进．

图1 车辆-道路几何模型Fig. 1 Vehicle-road geometric model

1.1 Pure Pursuit模型分析

Pure Pursuit模型是一种应用非常广泛的控制模型，最早由Wallace等[10]在1985年提出，该模型对各种路况都有很好的适应性． Pure Pursuit模型建立不需要考虑车辆动力学，也不要求路径的连续性和光滑性．通过调整参数，该模型可以满足多种场景的需要．因此，许多自主地面车辆都采用Pure Pursuit模型控制作为主要的横向控制．

在Pure Pursuit模型中，以后轴为控制中心，不考虑行驶阻力，将车轮假设成刚性的，简化阿克曼转向模型，即在转向时，假设前轴左右轮的转角是相等的，把四轮车辆模型简化成二轮自行车模型，如图2所示．

图2 自行车模型Fig. 2 Bicycle model

自行车模型可以将前轮转角与后轴行驶的路径曲率之间的关系进行简单描述，如式(1)所示．

经证实，在中低速场景下，式(1)能够较为准确地描述车辆运动．有了简化的阿克曼转向模型，Pure Pursuit模型便可建立，如图3所示．

图3 Pure Pursuit模型Fig. 3 Model of Pure Pursuit

该算法的核心思想是以车辆后轴中心为控制点，在期望路径上以距离ld向前确定一个预瞄点，假定车辆能够沿着某条平滑的路径安全的到达确定的点，然后根据车辆当前位姿、转弯半径以及预瞄距离来确定所需要的前轮转角，根据图3所示的几何模型，建立式(2)所示关系．

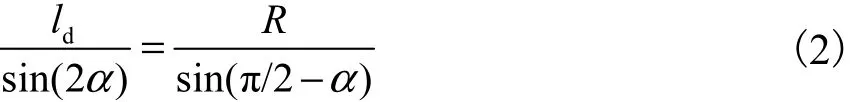
式中：ld表示预瞄距离；R表示转向半径；α表示车辆当前位置与目标点之间的偏角．

进一步可得式(3)

由式(1)、式(3)可得前轮转角和预瞄距离之间的关系

式(4)中的角度α可以通过几何关系得到

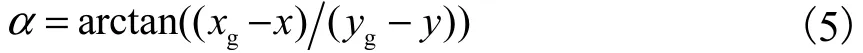
式中：gx、yg表示目标点的横纵向坐标；x、y表示车辆当前的横纵向坐标．

由式(4)可知，预瞄距离会直接影响前轮转角控制量，也就是说转角的大小一直是根据目标点的位置所决定的．以往的研究表明，较短的预瞄距离可以带来较小的跟踪误差，但车辆的稳定性较差；较长的预瞄距离可以带来更平滑的跟踪效果，但由于模型对弯道过于敏感，在曲率较大的路况下会出现车辆超前转弯，不能很好地贴合道路行驶的情况，对于路面车辆来说，严重偏离路径将会造成不可挽回的危险，如图4所示．

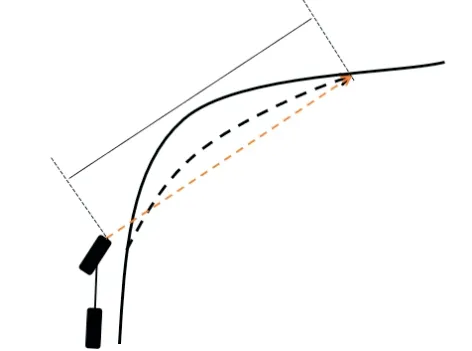
图4 车辆驶离弯道Fig. 4 Vehicle pulling away from the bend

预瞄距离的选择往往需要根据不同的道路场景进行大量的实验得出，稳定性和跟踪性能之间的折中选择是一个非常困难的工作，并且在调整控制参数时对路径的几何特征是非常依赖的[8]．

不同预瞄距离下的跟踪效果如图5所示．

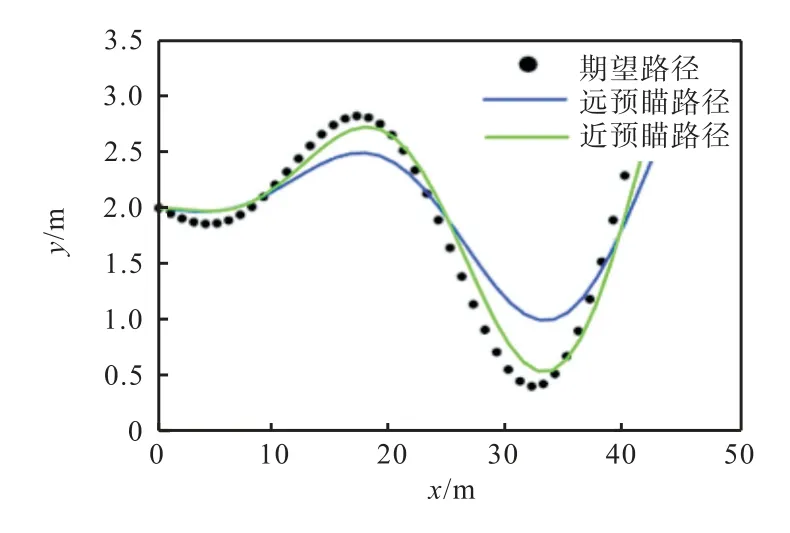
图5 不同预瞄距离下的跟踪效果Fig. 5 Tracking results at different preview distances

图5展示了在不同预瞄距离下，车辆实际行驶路径与期望路径之间的关系，可见不同的预瞄距离对控制效果有非常明显的影响．

1.2 Stanley模型分析

Stanley控制模型也叫前馈控制模型，如图6所示．在大地坐标系下，建立Stanley模型，该模型的核心思想是以车辆前轴中心为控制点，计算当前车辆与道路之间的偏差，包括车头朝向与道路方向的航向偏差以及车辆与道路的横向距离偏差，根据总偏差给出回到路径所需的前轮转角控制量．

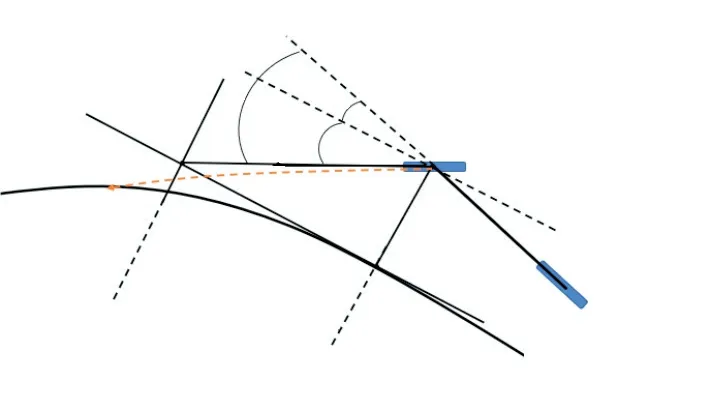
图6 Stanley模型Fig. 6 Model of Stanley

据此，建立关系式(6)

式中：δ为转角控制量；heθ和leθ分别为消除航向偏差和横向偏差的转角量；dl为预瞄距离；e为横向距离偏差．

车辆的航向偏差很容易修正，Stanley控制模型的难点在于消除横向偏差．假如车辆经过时间t达到目标点，可以得到横向距离偏差的关系式(7)

式(7)两边同时对t求导，可以得到横向距离偏差的变化率

当横向距离偏差很小时，可根据等价联动关系，得到式(9)

由式(7)—式(9)可得

式(10)对t积分，可得到横向距离偏差关于t的响应函数

Stanley模型的更优之处在于计算了车辆的横向偏差，并通过反馈的方式对这一偏差进行补偿，提高了跟踪的精度．但该模型对路径的平滑性要求较高，从式(11)可以看出，横向距离偏差以指数衰减，在速度过快或者预瞄距离较短的情况下容易出现控制超调，具体表现为在一些路况车辆会冲出道路和左右晃动，从图7仿真结果中可以看出，在弯道处由于超调使车辆偏离期望路径．

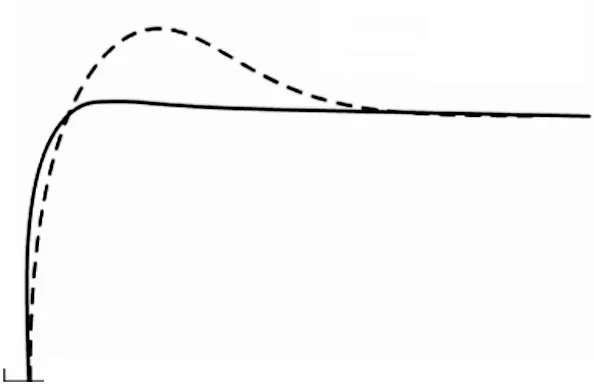
图7 路径偏离Fig. 7 Path deviation

由上述可知，基于几何跟踪的方式实现路径跟踪，不同的道路场景、控制模型以及不同的控制参数都会很大程度上影响跟踪效果．针对不同的工况，都需进行大量的实验得到较佳的控制参数，这不仅费时费力，而且不具有适用性．以往的实验表明，目前还没有一种单一的控制模型能够适应所有的路径条件．Pure Pursuit模型对道路的要求较低，工况适应较强，但跟踪精度受前向预瞄的影响较大，实际中需进行大量的实验来获取最优的预瞄参数．而Stanley模型，考虑了车辆的横向偏差，并通过前馈的方式对转角进行控制修正，提高了跟踪精度，但跟踪误差的快速收敛和控制超调之间的矛盾无法完全调和．

因此，本文建立了一种优化模型，同样基于几何关系的控制原理建立模型，对比上文讨论的两种模型，对以下方面做出改进．

(1)考虑车辆动力学约束．车辆动力学能够在高速和大曲率的场景下如实反映力与运动之间的关系，实现对行驶车辆的稳定控制，动力学模型具有强非线性时变的特征[11-12]，因此能够更加准确地反映车辆的运动关系.

(2)能够自适应预瞄．对于几何跟踪法，预瞄距离的存在会给模型本身控制精度带来一定的影响，而自适应策略会很大程度上提高模型在各种工况下的鲁棒性[13]．

(3)形成车辆-道路闭环控制．不管什么模型都不能完全地映射出真实情况，但是偏差是可以测量的，而模型的偏差预测和误差补偿是影响控制精度的关键因素[14]．

2 优化模型的建立

2.1 车辆动力学模型

要对车辆进行精确化控制，需要建立能够反映真实车辆且简单直观的数字化模型．为了准确描述车辆运动，需要建立更高阶、更稳定的控制关系，因此建立车辆动力学模型来更好地约束车辆运动，所建立的动力学模型如图8所示．

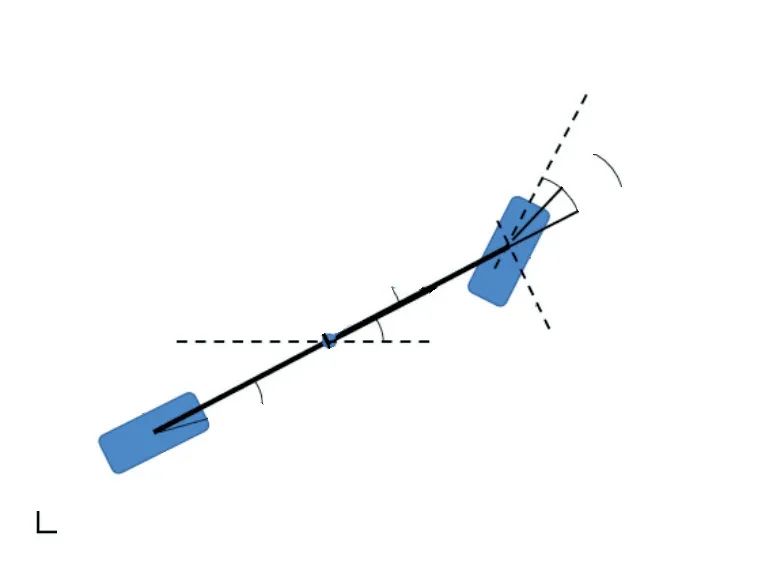
图8 动力学模型Fig. 8 Dynamics model

图8中，XOY为大地坐标系，xoy为车辆坐标系.根据车辆在y方向的受力关系，有

式中：m为车辆的质量；ay为车辆在y方向的加速度；fF和rF分别为车辆前轴和后轴的侧偏力；δ为前轮转角．

车辆在y方向的加速度由前向和横摆运动产生加速度分量组成，得如下关系

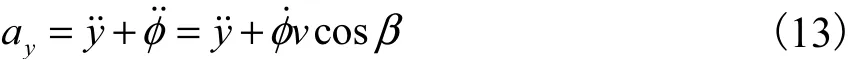
根据式(12)、式(13)可以得到

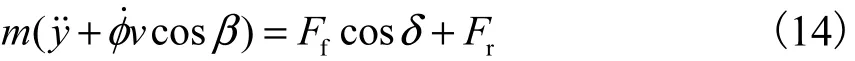
由力矩平衡可得：

式中：Iz为转动惯量；lf和lr分别为前轴和后轴到质心的距离．

对车轮进行受力分析，可得

式(16)和式(17)中：αf和αr分别为前后轮侧偏角．

侧偏力可以表示为

式(18)和式(19)中：kf和kr分别为前后轮侧偏刚度；fθ、rθ分别为前后轮实际方向角．

根据运动关系有

式(20)和(21)中：vfy为前轮沿y方向的速度；vyr为后轮沿y方向的速度．

式(22)和(23)中：y˙为车辆速度沿y方向的分量．根据式(16)—式(23)，可得

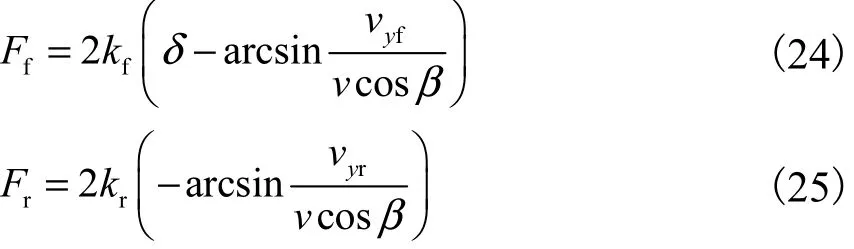
综上可得动力学约束关系为

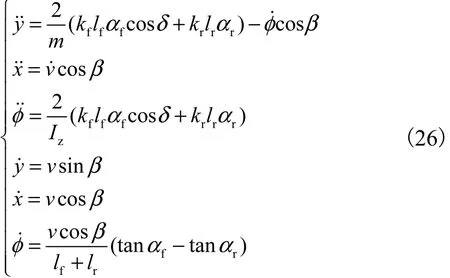
2.2 预瞄控制系统

由上述讨论可知，对于几何跟踪模型，预瞄距离的选取会直接影响跟踪精度．改进的优化模型设计了一种自适应预瞄策略，该策略会先确定一个预瞄区间，然后从预瞄区间内的路径点中选择最优目标点．

首先确定预瞄区间的起始点．一般来说，车速较快时，选择较远的路径点为目标点；而车速较慢时，选择离车辆较近的路径点更为合适．在弯道时，希望保留更多的路径信息，如图9所示，若求得当前车辆所在位置的道路曲率，则有

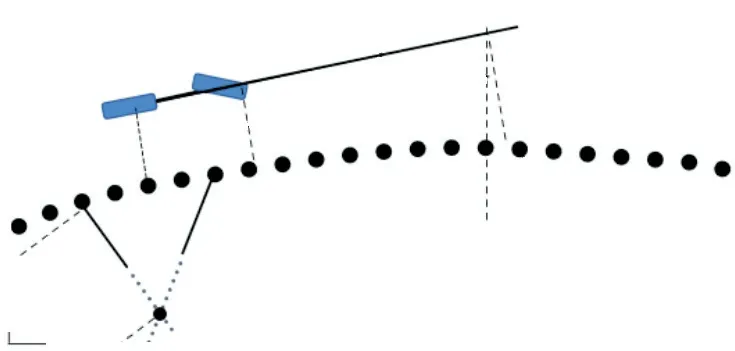
图9 预瞄起始点Fig. 9 Starting point of preview

式中：v为车速，为已知量；c为增益系数；k为该路径点处的曲率，确定方式见图10．

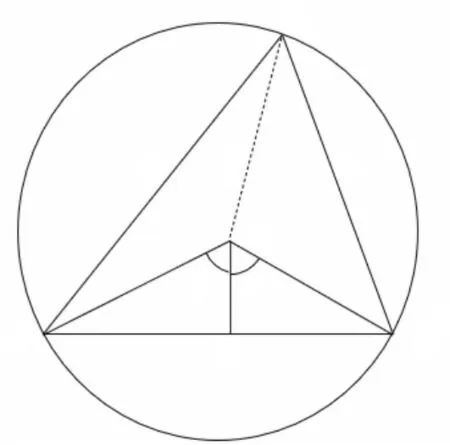
图10 求解曲率Fig. 10 Solving curvature

如图10所示，设A、C为与路径点B相邻的前后路径点，外圆为过A、B、C三点组成的三角形外接圆，通过式(28)可得到点B处的曲率k．

式(28)中的sinθ可通过三角形余弦定理求得，这样便可求得每一路径点的曲率．

在确定了预瞄起始点之后，便要确定预瞄终点，就可以知道当前车辆的预瞄区间．如图11所示，在大地坐标系下可以确定路径点和车辆的坐标，1g点为预瞄起始点，若以前轴中心为控制点，行驶到路径点1g需要的前轮转角控制量为f1δ，以后轴中心为控制点，则需要的前轮转角控制量为r1δ，假设r1δ小于f1δ，得到转角区间(r1δ，f1δ)．

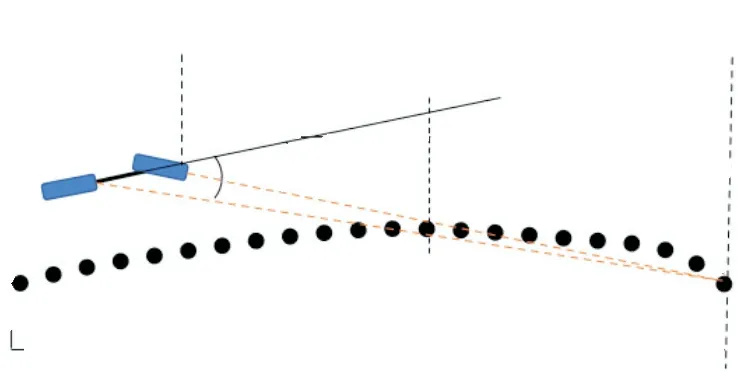
图11 预瞄终止点Fig. 11 Terminal point of preview

下面给出计算流程：

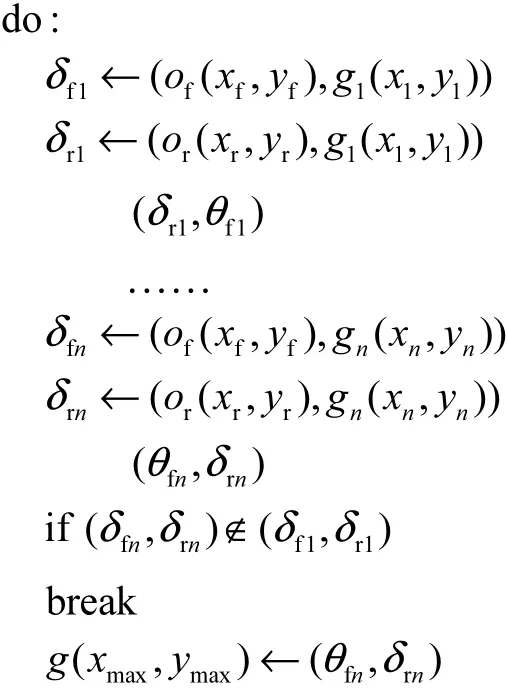
其中：of(xf,yf)、or(xr,yr)分别表示前后轮位置，gi(xi,yi)表示路径点坐标，g (xmax, ymax)就是计算得到的预瞄终止点．

在上一步计算得到预瞄区间之后，只需在预瞄区间内找到最佳预瞄点即可，预瞄区间内的点并不是都适合作为车辆下一个预瞄点，预瞄点的选择需要综合考虑车辆在路径跟随中的平顺性和预瞄横向偏差，评价标准为

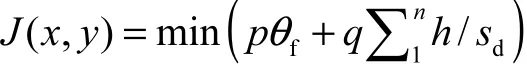
其中：J为损失函数，θf为航向偏差，为预瞄横向偏差(如图12，假设车辆欲到达路径点g，用直线表示车辆行驶到g点的轨迹为g点之前预瞄区间所有路径点到R的距离之和)，sd表示车辆与当前参考路径点之间的距离，p、q为控制参数．

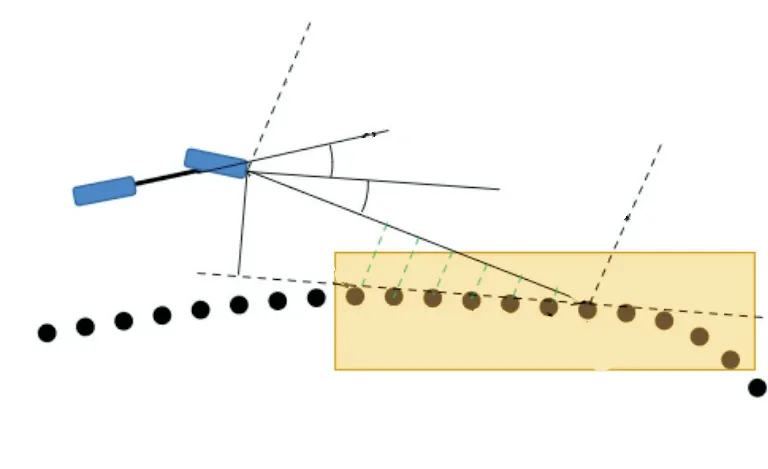
图12 选择最佳预瞄点Fig. 12 Selecting the best preview point

计算流程如下：

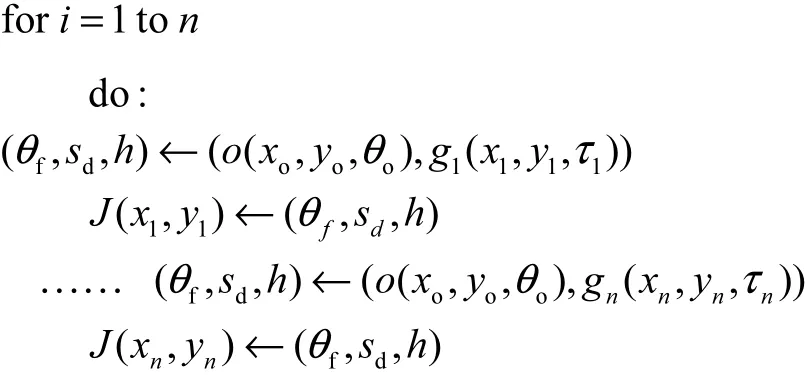
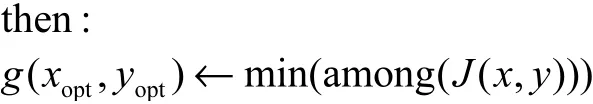
其中：o(xo,yo,θo)表示车辆的位置和航向角；gi(xi,yi,τi) 表示路径点位置和切线方向；g(xopt,yopt)就是损失代价最小对应的路径点．

2.3 横向控制系统

得到最佳的预瞄点之后，通过建立几何关系便可以得到车辆行驶至目标点所需要的转角控制量．

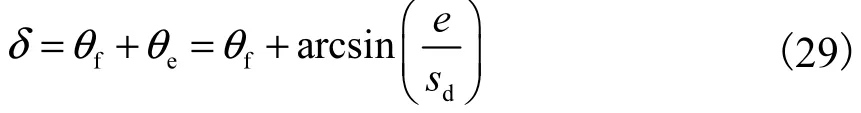
式中：fθ为车辆航向偏差补偿角；eθ为消除横向偏差的补偿角；e为横向距离偏差；sd为车辆到目标点的距离．

考虑到车轮的侧偏现象，最终的转角δreal还应考虑转向的不足．

式中：K表示转向梯度；ay为横向加速度；ga为重力加速度．

在本文所设计的控制器中，为使跟踪效果更好，依然对转角进行反馈补偿，但为使车辆更加平稳，式(30)中的参数K不仅仅表示转向梯度，同时也受横向距离偏差的影响．驾驶员控制车辆可以认为是一个不断反复进行的“信息感知—轨迹决策—操作校正”的过程[15]，因此该控制器由两部分组成，一是通过车辆-道路模型计算出所需的转角控制量，二是通过横向偏差计算补偿角，通过反馈对转角进行增益控制，控制流程如图13所示．

图13 控制流程Fig. 13 Control process

3 结果分析

为了呈现改进之后的模型效果，在Simulink中搭建优化模型，并与Prescan联合进行仿真测试，在每次实验中，实验车速和预瞄距离(预瞄距离仅针对Pure Pursuit 和Stanley模型)都设为固定值，车辆仿真参数见表1．

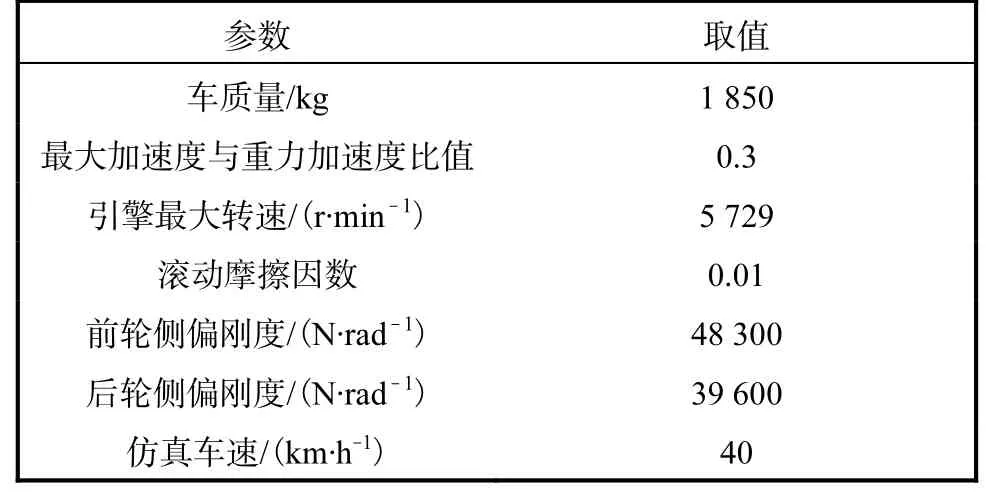
表1 车辆仿真参数Tab. 1 Vehicle parameter

3.1 仿真实验

本次仿真实验分别在预瞄距离为4、6、8m的情况下对比分析优化模型的跟踪效果和横向偏差(预瞄距离仅针对Pure Pursuit模型和Stanley模型)，结果如图14、15所示．

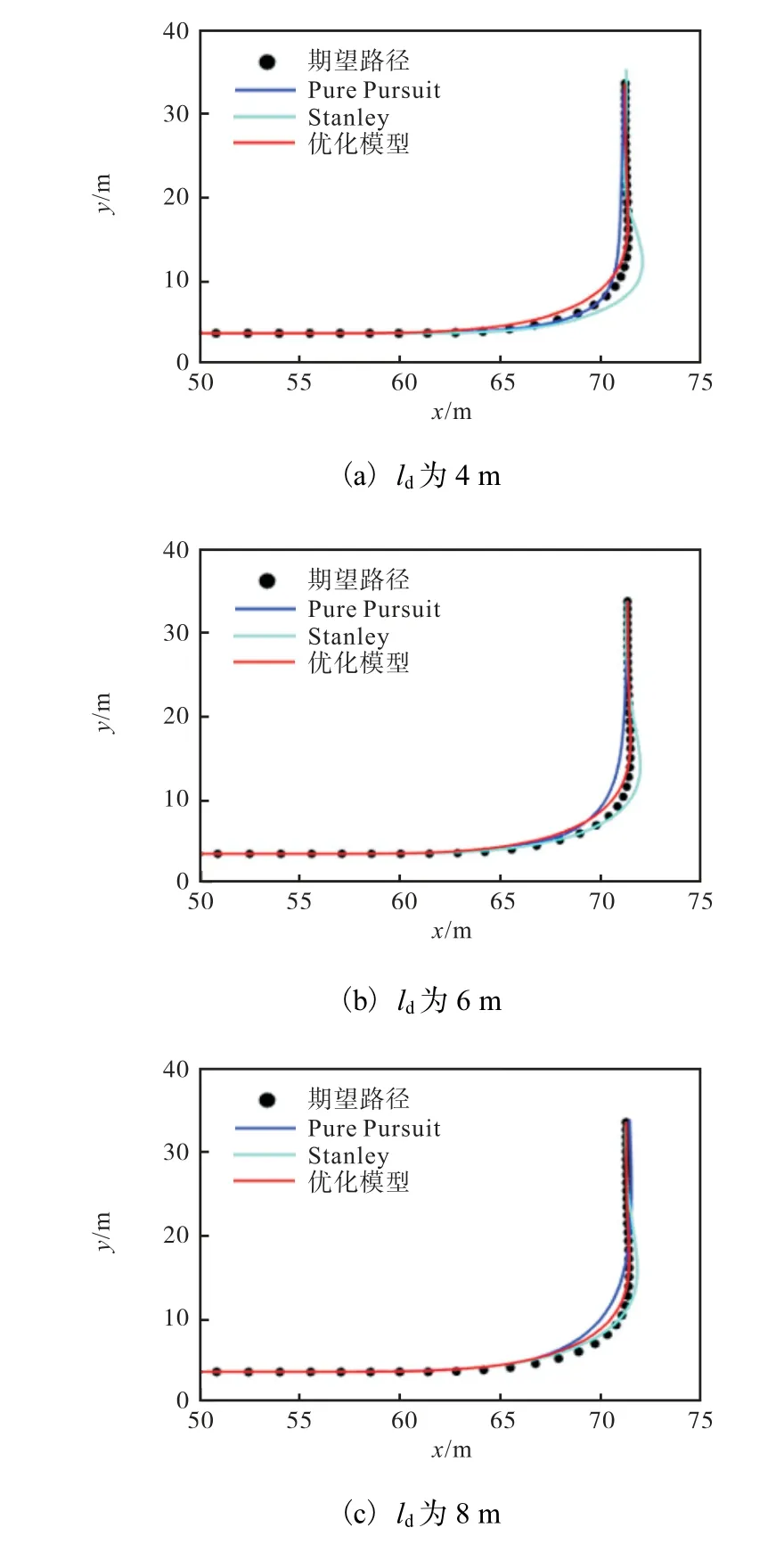
图14 不同ld下的跟踪效果Fig. 14 Tracking results of different ld

图15 不同ld下的横向偏差Fig. 15 Lateral errors of different ld

从跟踪结果图和横向偏差图可以看出，调整预瞄距离可以明显改善Pure Pursuit和Stanley模型的跟踪效果，在预瞄距离为4m时，Pure Pursuit 模型的最大横向偏差为0.8m左右，而预瞄距离为8m时的最大横向偏差接近1.6m．Stanley模型同样受到预瞄距离的影响，并且横向偏差曲线呈现小幅二次波形，这是之前所述的控制超调使车辆产生晃动所致．在某些时刻，前两种模型的跟踪效果比优化的模型要好，但自适应预瞄使得优化模型更加灵活，对于大曲率路段能够减少精度的损失．

同时在预瞄距离为6m时，分析了3种模型的航向角变化情况，结果如图16所示．从实验结果可以看出，即便采用了前馈控制，优化模型航向角变化非常平稳，而Stanley模型在转角处出现了转向过度的情况，在直线阶段也出现了微小的晃动(图16(b))，Pure Pursuit模型在弯道部分变化要延后一些，这是少许转向不足所致．总的来说，相较于前两种模型，优化模型的跟踪精度和控制平稳性都得到了提升．

图16 3种模型的航向角变化图Fig. 16 Changes of heading angle of three models

3.2 实车实验

实车平台如图17所示．

图17 实车实验平台Fig. 17 Vehicle experimental platform

实车实验所用的车辆为本实验团队基于大众速腾燃油车研发，通过外接的驾驶机器人系统对车辆进行控制，达到无人化的目的．驾驶机器人基本硬件设施为：1个激光雷达、1个前视主动安全摄像头、6个毫米波雷达(前后保险杠处分别装载3个)、1个车载工控机、1个组合导航系统．驾驶机器人结构包括1个转向控制器、1个油门控制、1个刹车控制器和1个挡位控制器．

本次实验所用到的惯导系统是华测公司推出的CGI-610型高精度MEMS组合导航接收机．本次实验对车辆采用RTK技术和惯导系统精确定位，基准站安装在空旷地带的高处，流动站安装在车辆后轴中心垂直上方的备胎处，定向天线位于车顶前方，定位天线位于车顶后方．通过安装在惯导上的4G网络进行数据通信，实验路段采集于一段校园路段，为了安全考虑，实验车速较低，在7m/s车速下完成实验．3.2.1 惯导标定与数据提取

首先进行惯导标定，标定参数见表2．

表2 惯导标定参数Tab. 2 INS configuration parameters

在标定好之后，通过CAN接口输出惯导信息，本次实验提取定位经度、定位纬度以及姿态角3个信号频道的数据，提取的GPS信息如图18所示．

图18 GPS信息Fig. 18 Information of GPS

3.2.2 实车结果分析

本次实车实验结果采用事后分析方式，通过两次惯导输出数据进行对比．实车实验结果如图19所示.由图19可知，优化模型对实车同样有很不错的控制效果，并且车辆全程行驶平顺，通过自适应预瞄和反馈修正使车辆控制更加平稳，同时也保证了跟踪精度．但在弯道处出现了少许的转向不足，如图19(e)中，弯道处最大横向偏差达到1.6m左右，当然其中包含着转向机构的控制误差和定位误差，应当进一步修正．

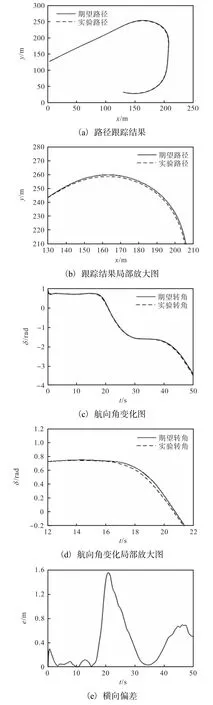
图19 实车实验结果Fig. 19 Experimental results of actual vehicle

4 结 语

在无人驾驶路径跟踪领域，基于几何关系的几何跟踪法是一种可靠性很高的方法，如今已经成功实现产品化．但由于模型无法完全反映真实场景，智能算法也无法代替驾驶员操控，导致在极限工况下，最后的跟踪效果都不尽人意，但通过不断地改进优化，控制模型可以满足更多的场景需要．

现在知名度较高的几何跟踪模型包括Pure Pursuit模型和Stanley模型，这两种控制模型已被应用到了各种场景，但由于模型的先天不足，且预瞄距离对转角控制影响较大，导致在极限工况下跟踪效果并不好，甚至还可能出现驶离道路的现象．

本文优化的模型提高了模型控制的稳定性，且没有增加模型的复杂度，对于改进路面车辆同样有促进作用；但优化模型的局限或者说当前的几何跟踪模型都没有考虑车辆和道路的几何形状，也没有将横向控制和纵向控制进行耦合，这也是未来路径跟踪需要考虑的问题．据以往的研究表明，在车速过快或蜿蜒曲折道路的工况下，几何式的控制效果明显不如在中低速和平整道路工况下，为解决这个问题，一个可行的方法就是结合模型控制的方法，在不同的工况下采用不同的控制方法，提高车辆路径跟踪的稳定性．