基于不确定故障树的软件可靠性分析方法
刘 颖,杨芸芸
(天津科技大学人工智能学院,天津300457)
软件可靠性分析是软件可靠性工程的核心内容之一.软件失效不仅会造成硬件系统瘫痪和经济损失,还会引起重大事故,如美国长途电话业务曾因软件故障引发系统瘫痪、火箭发动机控制系统软件故障可能会造成飞行试验失败、飞机的飞行控制软件的失效会危及人身安全等.因此,科学的软件可靠性评估是非常必要的.软件可靠性指在一定的条件下和时间内,软件运行不会发生故障的概率[1].故障树是常用的软件可靠性评估方法,该方法适用于软件生命周期的各阶段.刘文红等[2]针对软件测试用例设计不充分问题,提出一种通过故障树分析设计测试用例的新方法.以上文献均采用传统故障树分析方法评估软件的可靠性,即假设基本事件故障概率是常数或随机变量,但概率假设只能用来评估随机不确定性.
在软件可靠性测试过程中,受到软件内部结构的复杂性、人的认知水平等原因的影响,存在许多认知不确定性因素,因而无法采用传统软件可靠性评估. 针对不精确的信息,专家学者开始引入模糊理论[3]对其进行描述.蔡开元[4]提出了基于模糊理论的软件可靠性增长模型,该模型不仅适用于测试阶段,而且适用于确认阶段.焦彦平等[5]针对软件开发初期信息不完全的问题,基于模糊集理论建立软件缺陷评估模型.谭海中[6]针对传统通信软件可靠性测试计算结果不精确的问题,提出了采用模糊故障树的可靠性测试方法.但由于可能性测度不满足自对偶性,导致评估结果经常产生相互矛盾的结论.
不确定理论[7]是基于规范性、自对偶性、次可加性和乘积公理体系的数学分支,主要用于对认知不确定性建模.近年来,不确定理论在许多领域已经有了广泛应用,如系统可靠性建模[8]、结构可靠性评估[9]、图论[10]、不确定统计[11]、时间序列模型[12]等.
本文在认知不确定性环境下,提出基于不确定故障树的软件可靠性分析方法,并用于实际装备软件的可靠性评估.
1 基本概念
1.1 不确定理论
令Γ为非空集合,L是Γ上的子集构成的σ-代数,L中的每一个元素Λ称为事件.每个事件Λ发生的信度记作 M{Λ},其中信度M需要满足以下4条公理:
公理1(规范性)对于全集Γ,有
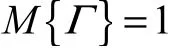
公理2(自对偶性)对任意事件Λ∈L,有
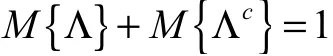
公理3(次可加性)对任意的可列可数事件列Λ1, Λ2,… ,有
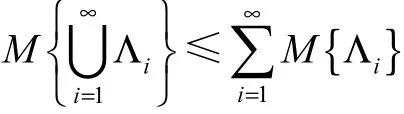
公理4(乘积公理)令(Γk, Λk,Mk)为不确定空间,k=1,2,… ,则乘积不确定测度满足
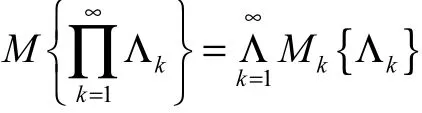
定义1若集函数满足规范性、自对偶性、次可加性和乘积公理,则称其为非空集合上的不确定测度.
定义2令Γ是一个非空集合,L是一个在Γ上的σ-代数,M是一个不确定测度,则称三元组(Γ,L,M)为一个不确定空间.
定义3不确定变量是一个从不确定空间(Γ,L,M)到实数集的函数ξ,{ξ∈B}是一个在任意Borel集上的事件.
定义4对任意Borel集的实数 B1,B2,… ,Bn,若满足
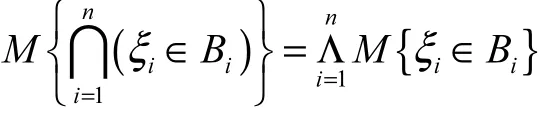
则不确定变量ξ1,ξ2,… ,ξn是相互独立的.
定理1对任意Borel集实数 B1,B2,… ,Bn,若满足
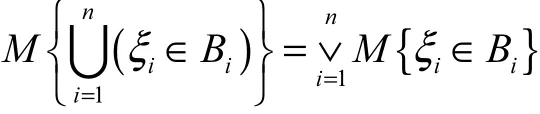
则不确定变量ξ1,ξ2,… ,ξn是相互独立的.
定义5一个不确定集合是一个从不确定空间(Γ,L,M)映射到实数集合的函数ξ,{ B ⊂ξ}和{ξ⊂ }B是对于任意Borel集的事件.
定理2令ξ和η为不确定集合,则
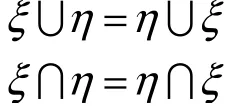
定理3令ξ,,ητ为不确定集合,则
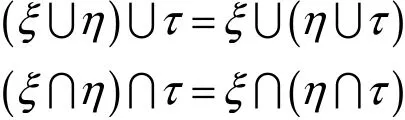
定理4令ξ,,ητ为不确定集合,则
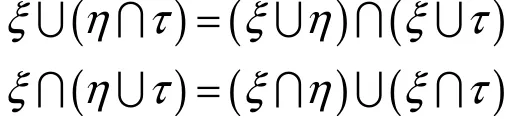
定理5令,ξη为不确定集合,则
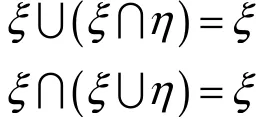
1.2 不确定故障树分析法
故障树可以用来对软件风险或可靠性进行定量评估,并分析引起软件产品发生故障的原因,包括软件产品组成部分、软件使用环境、人为因素等,适用于大型复杂系统.
故障树分析法遵循自顶向下原则.分析系统的故障模式时,将故障模式作为输出事件(顶事件),用“中间事件”表示导致该事件发生的原因,并用逻辑门(“与门”、“或门”)连接.以此类推,直到找到顶事件发生的根本原因,即输入事件(基本事件).
定义6在故障树中,若所有基本事件发生的信度均用不确定测度评估,则该故障树称为不确定故障树.
定理6若输入事件 Λ1,Λ2,… ,Λn相互独立且由“与门”连接,则输出事件Λ发生的信度为
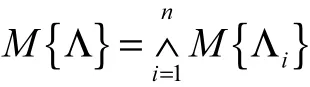
若输入事件 Λ1,Λ2,… ,Λn相互独立且由“或门”连接,则输出事件Λ发生的信度为其中:∨为最大值运算符,∧为最小值运算符.
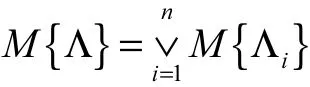
2 本文方法的流程
(1)根据软件系统控制流程图,建立故障树.基本事件是软件各最小模块单元,各最小模块单元分别具有对应的代码块,中间事件为控制流程中间子程序模块,顶事件为软件故障.在可靠性测试过程中,以最小模块单元的代码块的失效数据为依据,进行可靠性评估.
(2)获取基本事件发生的不确定测度.在没有足够测试数据的情况下,邀请软件工程师给出基本事件发生的不确定测度.
(3)由树形结构给出顶事件的表达式.将顶事件用基本事件表示,若存在不相互独立的中间事件,利用不确定集合的运算法则化为相互独立的基本事件.
(4)进行软件可靠性评估.利用不确定理论的运算法则,结合故障树,对软件可靠性进行评估.
(5)进行敏感度分析.分析故障树中基本事件的敏感度.在进行测试用例设计时,考虑各模块单元对系统失效的影响程度,重点测试关键模块.
利用不确定故障树分析法的基本步骤,为软件生命周期中的各个阶段建立失效模型,计算软件失效的可能性,通过分析结果提出保障意见,从而提高软件安全性.
3 某装备软件可靠性分析
对某装备软件系统进行实例分析.该软件的功能是实时监测某飞行控制系统的传感器,在飞行控制系统的正常工作过程中有重要作用.由于软件的使用环境等原因,没有大量的故障测试数据,无法使用概率方法,因此利用本文的方法,为该装备软件进行可靠性评估.
(1)对某装备软件的控制流程进行分析,软件故障是顶事件,控制流程中间的子程序模块故障是中间事件,软件各最小模块单元是基本事件,各最小模块单元分别具有对应的代码块.建立如图1所示的不确定故障树[12],其中,1,2,...,nΛ Λ Λ为相互独立的基本事件,各最小模块单元所包含的代码块行数见表1,为中间事件,Λ是顶事件.
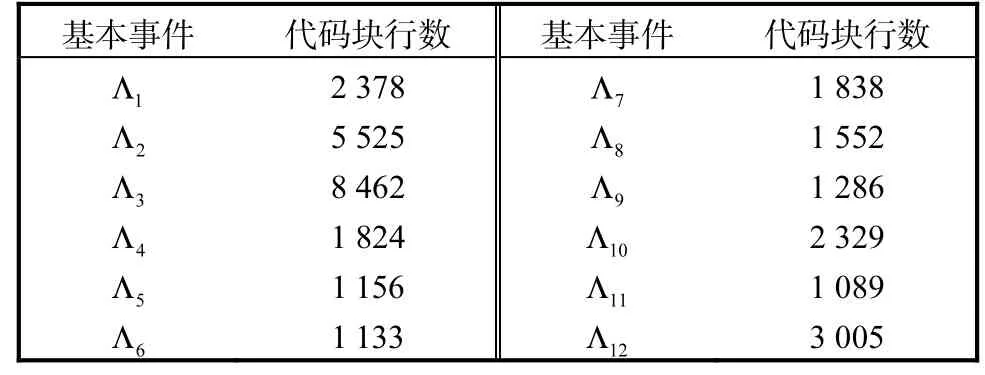
表1 基本事件对应的代码块行数Tab. 1 Numbersof lines of code corresponding to the basic event
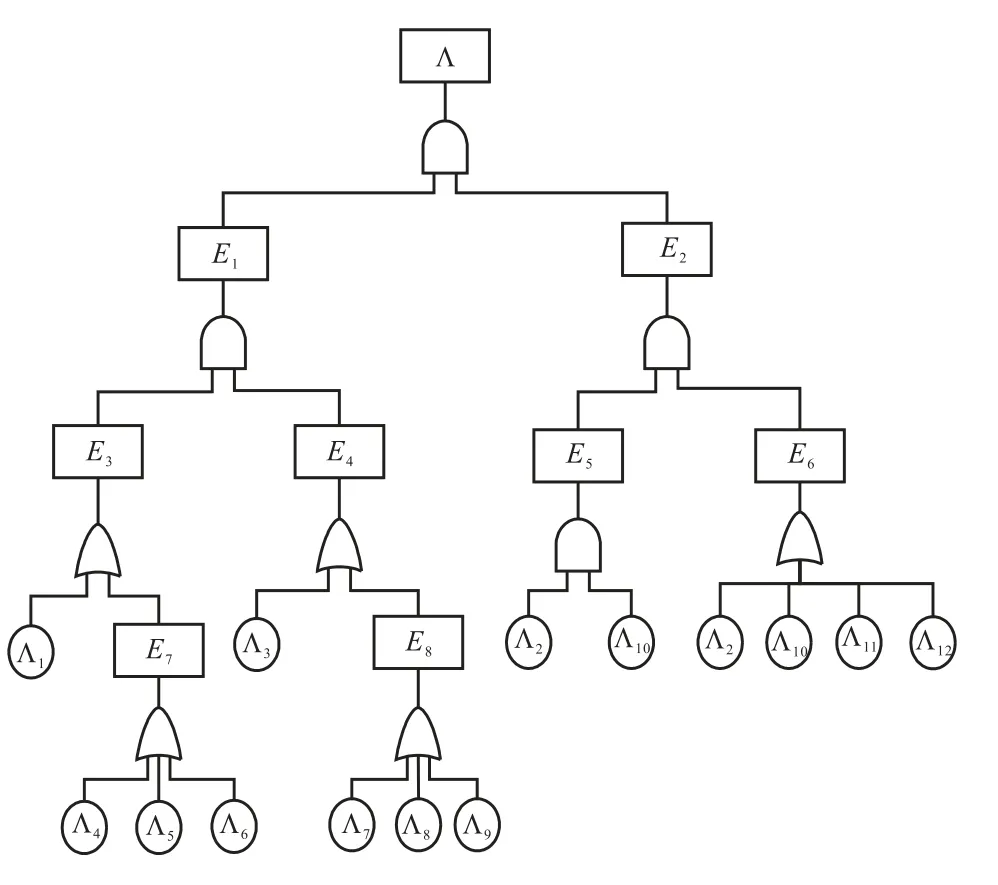
图1 某装备软件的故障树示意图Fig. 1 Fault tree diagram of a certain equipment software
(2)由于软件测试中的故障数据量较少,输入事件(每个代码块中发生故障的信度)是由专家评估得出(表2).
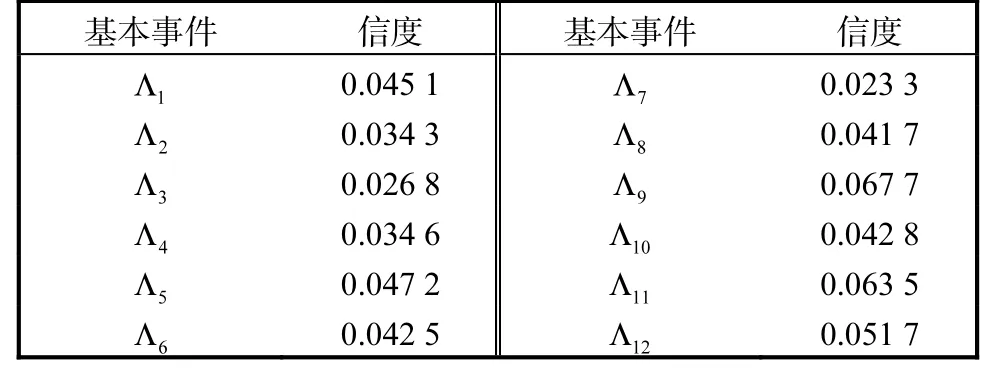
表2 基本事件故障信度数据Tab. 2 Failure belief degrees data of the basic events
(3)由图1中的树形结构,结合定理2、定理3、定理4和定理5,从而得到输出事件为
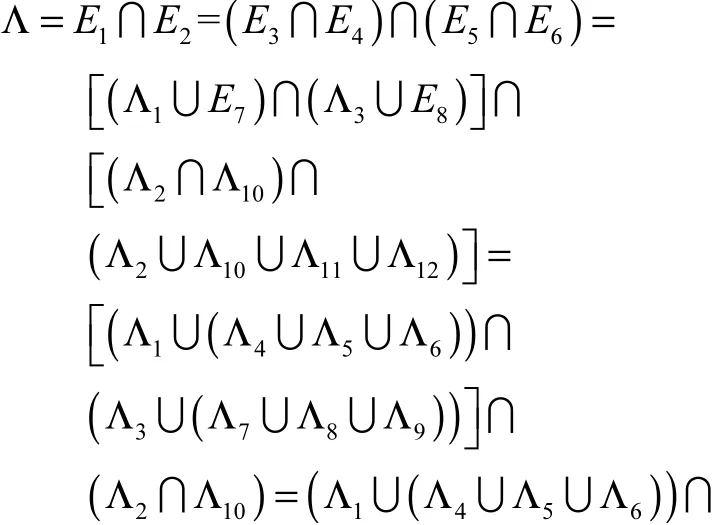

(4)根据定义4、定理1得出系统的故障信度为
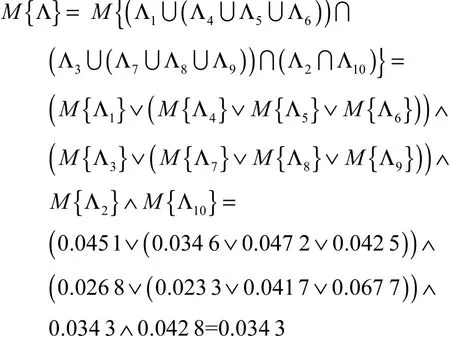
故系统的可靠度为
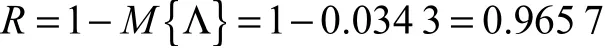
(5)在对软件系统进行可靠性评价时,由于基本事件 Λ1, Λ2,… ,Λ10对顶事件的影响程度不同,因此采用Sobol灵敏度分析方法对基本事件 Λ1, Λ2,… ,Λ10进行敏感度分析并进行评价,见表3.
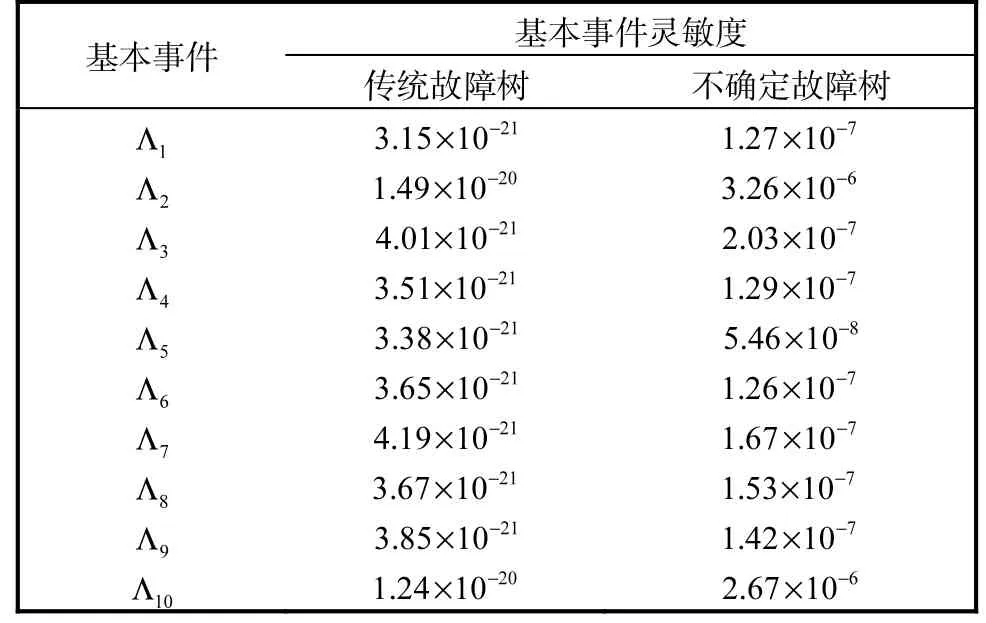
表3 基本事件灵敏度对比表Tab. 3 Comparison table of basic event sensitivity
从表3可以看出,基于本文提出的方法得到的基本事件灵敏度值均高于基于传统故障树的基本事件灵敏度值,代码块行数分别为5525和2329的基本事件Λ2和Λ10的灵敏度值最大.因此,基本事件的高灵敏度证明了基于不确定故障树的软件可靠性评估方法可以对软件可靠性进行精准测试.下面具体分析敏感参数对软件系统可靠性的影响情况.
图2为基本事件Λ2和Λ10的变化对软件系统可靠度的影响情况示意图.在(0,0.043)内,软件产品可靠度随着基本事件Λ2发生失效的不确定测度的增大而减小,之后产品失效的不确定测度不再变化.在(0,0.0343)内,系统可靠度随Λ10的增大而减小;在0.0343以后,系统可靠度则不再变化.
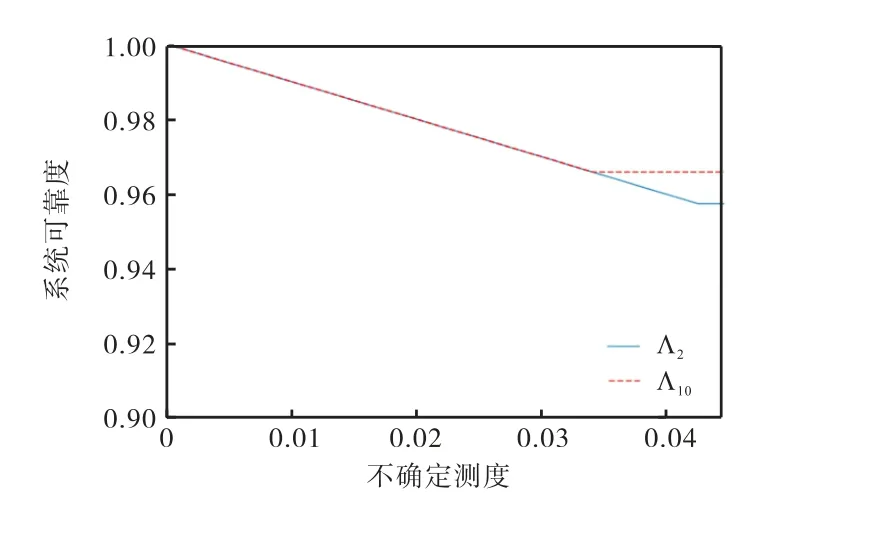
图2 基本事件Λ2和Λ10对产品影响情况示意图Fig. 2 Schematic diagram of impact of basic events Λ2 and Λ10 on products
综上所述,应该重点关注代码块行数为5525和2329的代码块所对应的最小模块单元,因为这两个最小模块单元对产品可靠度影响较大,是测试的重点.
4 结 语
在软件可靠性分析过程中,由于没有充足的故障数据且存在大量的认知不确定性,基于传统概率论的故障树分析方法不再适用,故本文针对传统故障树对软件可靠性分析不足,提出不确定故障树软件可靠性分析方法,主要创新内容:
(1)最小模块单元的代码块中发生故障的信度用不确定测度评估.
(2)在不确定故障树中,采用不确定集合运算法则,可将不相互独立的中间事件转化为相互独立的基本事件.
(3)对基本事件进行敏感度分析,找出影响软件可靠性的关键因素.

