粗糙表面切向接触模型的数值分析与实验研究

许刚,李卫,黄平,占旺龙

(1.华南理工大学机械与汽车工程学院, 510640, 广州; 2.深圳技术大学中德智能制造学院, 518118, 广东深圳)

在工程应用中,机械组件往往是通过各个零件表面搭接形成关节而组装在一起。由于关节处连接表面通常是凹凸不平的,在法向载荷作用下,表面粗糙处会先产生接触并被压缩,最终产生较大的法向变形[1]。然而,由于机器内部零部件的不断运动,连接表面将产生周期性的小幅切向位移(小于50 μm),此时连接界面周期性的切向位移称为微动。由于受到循环接触应力的作用,微动会导致连接处裂纹成核和磨损损坏,影响搭接部件的功能[2],缩短其使用寿命;在严重的情况下,组件损坏会引发或促进其他故障机制,进而影响结构的整体运行。另一方面,连接界面微动过程中的滑移现象是摩擦能量损失及阻尼的主要来源[3-4]。因此,研究粗糙表面的微动滑移特性具有重要意义。

在粗糙界面切向接触方面,Iwan模型[5-7]被广泛使用,它是由弹簧和滑动摩阻片组成的詹金斯单元串-并联而成,将此模型与关节表面各粗糙峰受法向载荷进行对比,恰巧发现了相似之处。用Iwan模型代替两粗糙表面间的接触,连接表面微滑动过程中的黏着、局部滑移和大滑移现象得到了有效的解释。目前,Iwan模型已经过Segalman[6]、Argatov和Butcher[8]、Zhan和Huang[9]、LI[10]等的开发和研究,进一步完善该模型的物理意义。

在微动过程中,关节界面的切向刚度、阻尼与摩擦系数等接触参数和能量耗散可以通过微动迟滞环来量化[10-12]。微动响应通常以力-位移环为特征,由于施加的切向位移一般小于50 μm,必须进行高精度的微动实验,才能保证以上测量参数的准确性[13-16]。目前,关节界面切向接触的理论模型研究和实验研究工作基本是相互独立的,现有的切向接触模型往往缺少实验验证。本文针对这一不足,利用与表面形貌相关的KE模型[17-18],进一步简化和推导切向接触的力-位移本构关系,利用可测量的接触参数,赋予Iwan模型各参数物理意义,并且该模型具有更简单的解析形式。最后,通过设计的装置进行实验,将构建的切向模型数值结果与实验结果进行对比,分析误差原因,为今后预测连接界面的微动响应提供依据。

1 切向接触模型

一般可以将随机粗糙面的接触问题,简化成刚性平面与曲率半径相同、高度随机分布的球形粗糙峰之间的接触[19-21],各粗糙峰之间的相互作用可忽略(见图1)。两表面粗糙度的均方根分别为σ1、σ2,σ为当量粗糙平面的均方根,h为刚性平面与当量粗糙表面中心线间的距离,z为粗糙峰顶部到到中心线的距离,ω=z-h为粗糙峰的法向干涉量,表面粗糙度参数为β=ηRσ,η为接触区域粗糙峰的面密度,R为粗糙峰的半径。令An为名义的接触面积,总的粗糙峰数量可以表示为N=ηAn,其中两粗糙表面发生接触的粗糙峰数量为

(1)

式中:φ(z)为粗糙峰高度的概率分布函数。

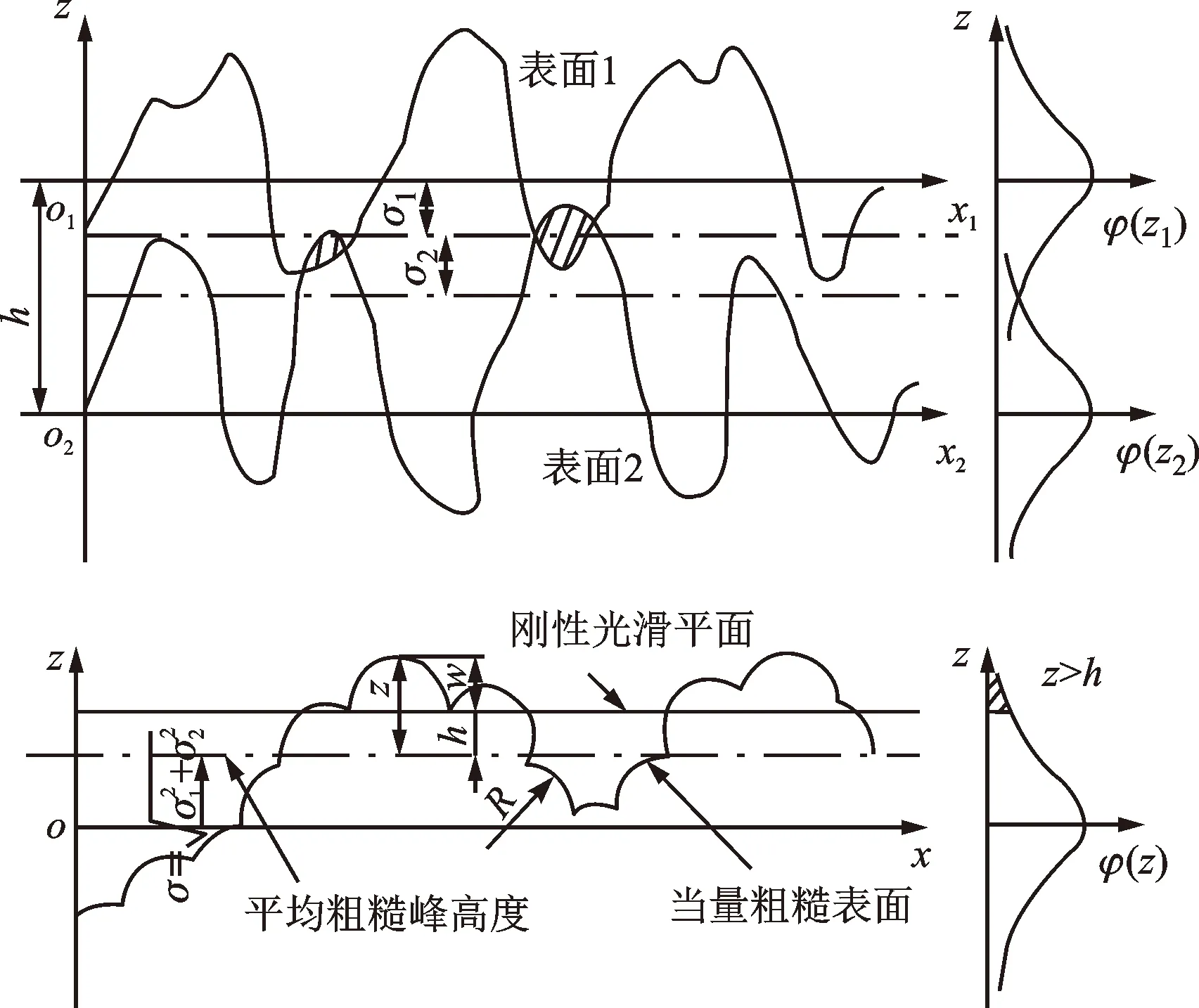
图1 两粗糙表面的接触Fig.1 Contact between two rough surfaces

对一般工程表面,当微凸体呈高斯分布时,即φ(z)-N(0,σa)。在法向力的作用下,高度高于h的粗糙峰将发生接触,承受法向力;高度低于h的粗糙峰不发生接触,不承受法向力。σ和σa分别代表粗糙表面和粗糙峰的标准差,根据McCool准则[20],两者之间的关系为

(2)

根据KE模型[17],当ω非常小,即ω/ωc<1时,单个微凸体发生弹性变形;当1<ω/ωc≤110时,微凸体发生弹塑性变形;当ω/ωc≥110时,微凸体则开始发生完全塑性变形。其中ωc=(πKH/2E)2R为微凸体开始发生弹塑性变形时的临界法向干涉,对应的临界法向力Wc=2/3KHπωcR,K为最大应力接触系数,H为较软材料硬度值,E为赫兹弹性模量。当微凸体发生弹性、弹塑性、完全塑性变形时,相应的法向力-位移表达式为

(3)

两粗糙平面接触时,法向力是由各高度不同的粗糙峰承受,表达式如下

(4)

对z进行无量纲化

(5)

(6)

式中:带星号(*)的长度变量都是用高度分布均方根σ进行无量纲化后的变量;W*(d)是进行无量纲化后的法向力变量。

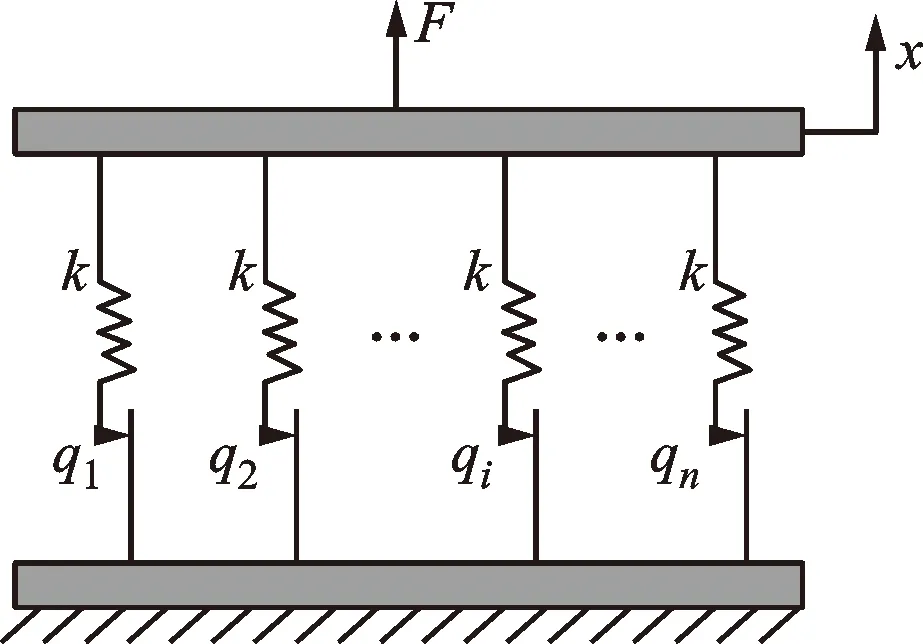
图2 串-并联Iwan模型Fig.2 Iwan parallel-series model

Iwan模型是由包含弹簧和滑动摩阻片组成的詹金斯单元并串联而成[22],每个詹金斯单元是由刚度为k的线性弹簧和屈服力为qi的库伦摩阻片串联构成,如图2所示。在表面间切向力F的作用下,F与切向位移x有以下关系[5-9]

(7)

进一步,令

x=σx*;q=kσφ;k2σ2ρ(q)=ρ*(φ)

(8)

得到

(9)

式中:ρ(q)为摩阻片临界滑移力的概率分布函数;φ为无量纲的摩阻片临界滑移力。式(9)中,等式右侧第1项为处于滑动状态下所有詹金斯单元的合力,第2项为处于黏着状态下所有詹金斯单元的合力。当两平面处于大滑移状态时,所有的詹金斯单元都处于滑动状态,等式第2项消失,此时式(9)将变为

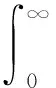
(10)

另外,根据库伦摩擦定律,在大滑移状态下,式(6)将变为

F*=fW*(h*)=

(11)

式中:f为摩擦系数。

将式(10)与式(11)对比分析,可得摩阻片滑移屈服力的概率分布函数为

(12)

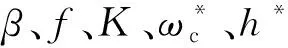
2 实验分析

2.1 实验装置介绍

微动实验主要用于研究机械关节在准静态和动态载荷情况下的微动行为,通过实验提取的接触参数高度依赖于所测得的迟滞环的形状,因此进行高精度的实验非常有必要。实验台结构如图3所示,实验台设计严格对称,有很好的对中性。压电陶瓷促动器是实验台的激励装置,用于施加切向位移,具有亚纳米级分辨率。使用一对同轴激光来测量实际的微动位移,分辨率达0.25 μm。三轴力称重传感器用于采集固定端样品承受的切向力以及实时监控未对准力,其z向刚度高达1.75 kN/μm,远远大于关节处的切向刚度。因此在实验中,关节固定端自身柔性而产生的形变可以忽略不计,满足切向力测量的高精度要求。预紧力通过压力垫圈实时监控,过渡部件使摩擦副的更换更加方便,再通过Labview软件同步采集力-位移数据。该实验台可直接测量微动过程中施加的位移与切向力,不需要对获得的数据进行后处理即可获得微动环。

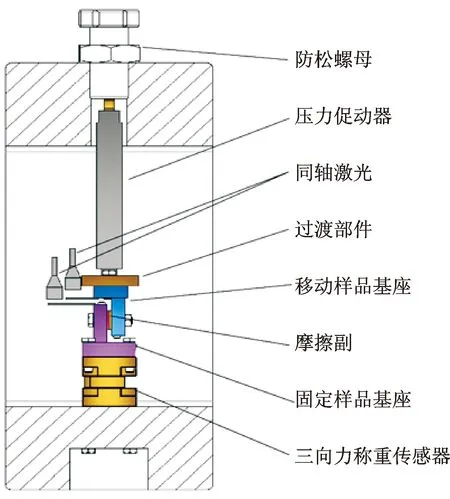
图3 实验台结构图Fig.3 Structure of experimental platform

此外,关节样品采用了特殊的设计,如图4所示。移动端和固定端都是由基座和摩擦副组成的,更换摩擦副即可进行不同工况、不同材料下的实验。摩擦副形状简单,可极大提高加工效率,节省加工成本。摩擦副中部的螺栓孔采用腰孔设计,可避免在微动过程中螺栓与摩擦副接触,导致迟滞环尖端产生“隆起”现象[15]。

(a)实物图

2.2 实验结果分析

本实验采用铝合金和Q235作为摩擦副材料,两者的材料参数见表1。摩擦副理论接触面积为272.6 mm2,经过铣削加工而成,表面粗糙峰呈高斯分布。先使用超声波清洁器对其表面进行清洗,以清除表面上的磨损碎屑和松散颗粒,再使用轮廓扫描仪对接触表面进行扫描,如图5所示。沿切向位移加载方向取3处,长度为3 mm,测得铝合金摩擦副和Q235摩擦副的粗糙度分别为1.26 μm和2.47 μm。所有测试均在室温、频率为2.5 Hz的情况下进行的,每次测试完需对预紧力螺栓进行卸载再重新施加预紧力,保证相同的测试条件。

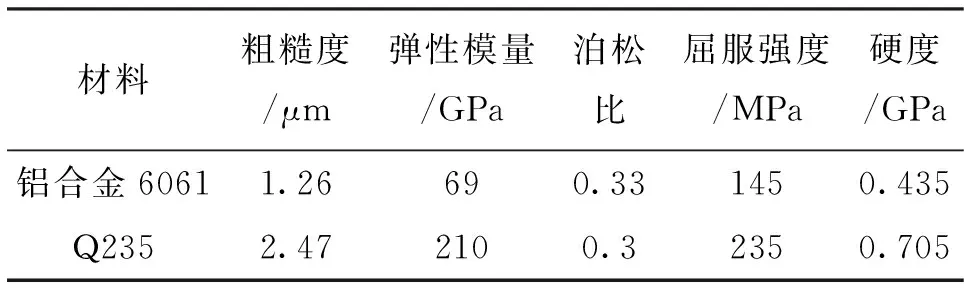
表1 摩擦副材料和几何参数

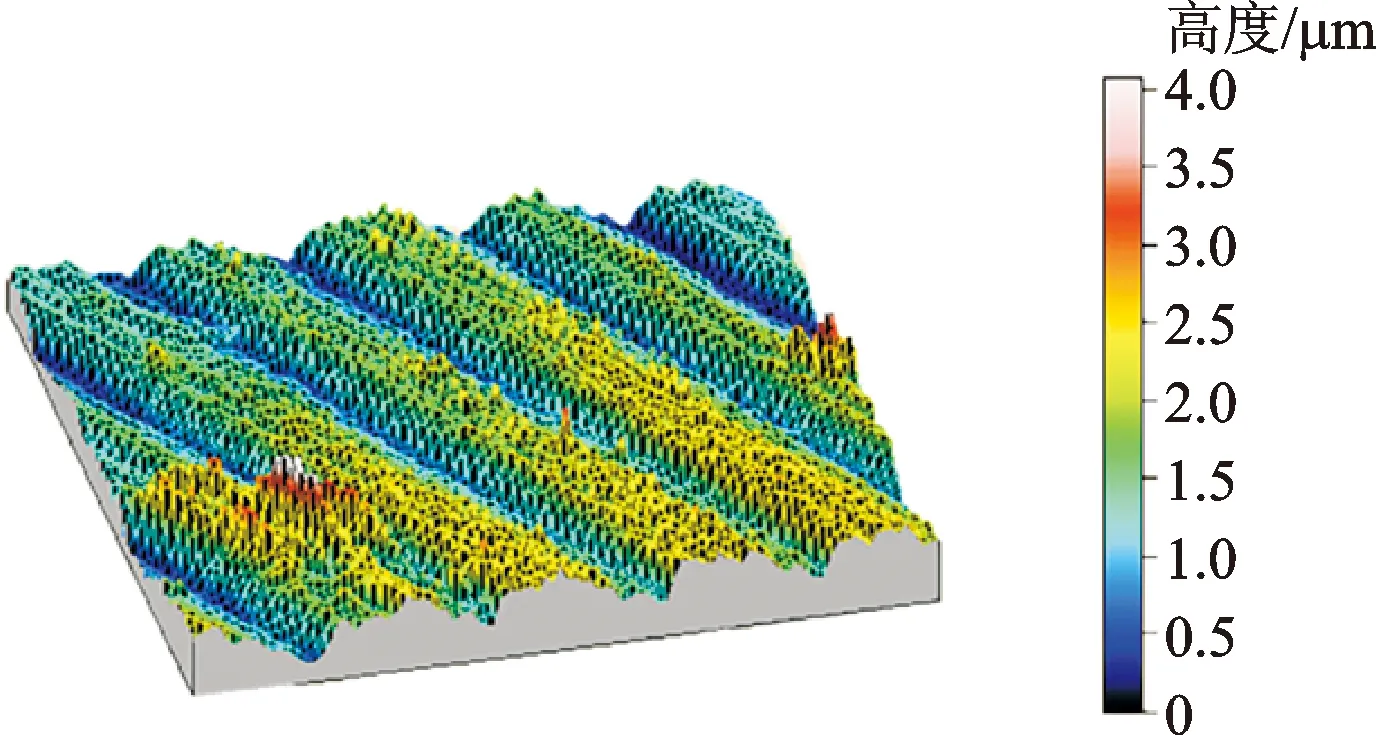
图5 摩擦副表面形貌Fig.5 Surface morphology of friction pair

2.2.1 稳定性测试 为选取适合的数据用于实验分析,需对实验数据进行稳定性分析。首先,对同一对摩擦副(Q235)进行3次组装,当预紧力W=250 N、激励幅值Δs=25 μm时,测量摩擦副产生的切向位移和切向力,将3次测得的数据进行比较,具有很好的重复性;其次,每次测试切向力在微动的前几个周期波动比较大,不适合当做最终实验数据进行分析,见图6a,故前几个周期生成的迟滞环也有很大的差异,见图6b,其中蓝色线条为各个周期形成的迟滞环在力-位移方向上的投影。因此,对前几个周期的数据进行比较分析是十分有必要的。表2列出了相邻两周期切向力数据的误差,可以看出,从第6周期开始,下一周期切向力的测量结果相比上一周期的误差小0.5%,故可认为,从第6个周期之后,摩擦副的微动趋于稳定。本文后续所有迟滞环数据均取测试过程中第8个周期的数据。

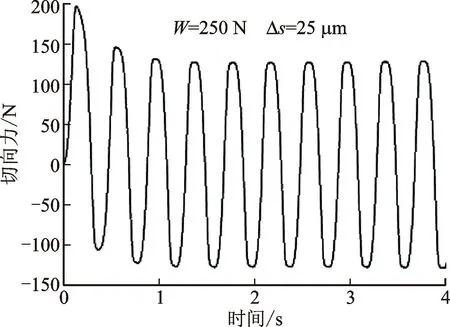
(a)前10个周期切向力数据

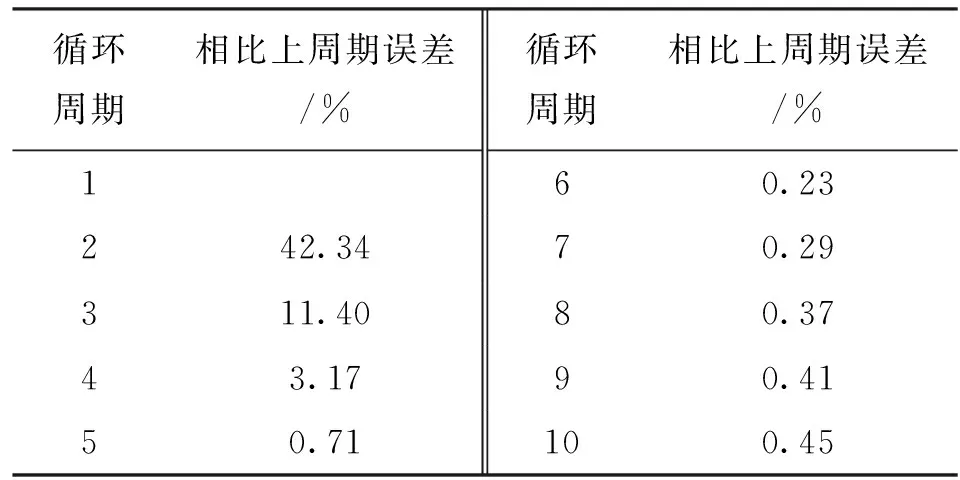
表2 力-位移迟滞环误差分析

2.2.2 预紧力和激励振幅的影响 对Q235摩擦副和铝合金摩擦副施加恒定的激励振幅(Δs=25 μm)和不同的预紧力,用于研究预紧力对摩擦副微动行为的影响。图7描绘了摩擦副在相同的正弦激励(Δs=25 μm)和不同的预紧力(W=100,250,400 N)下的迟滞回线,可见,预紧力对微动环的形状有很大影响。当施加相同振幅的正弦位移,预紧力较小时,摩擦力不足以防止界面打滑,很快就产生了大滑移现象;随着预紧力的增大,同轴激光测得的实际运动位移与理论施加的位移差距变大,连接界面滑动幅值减小,并逐渐过渡到局部滑移状态。对比图7a与图7b,施加相同的预紧力和激励幅值,Q235摩擦副的连接界面的切向刚度很明显高于铝合金摩擦副的切向刚度,且随着预紧力增大,两者的切向刚度有很明显的增加,如图8所示。

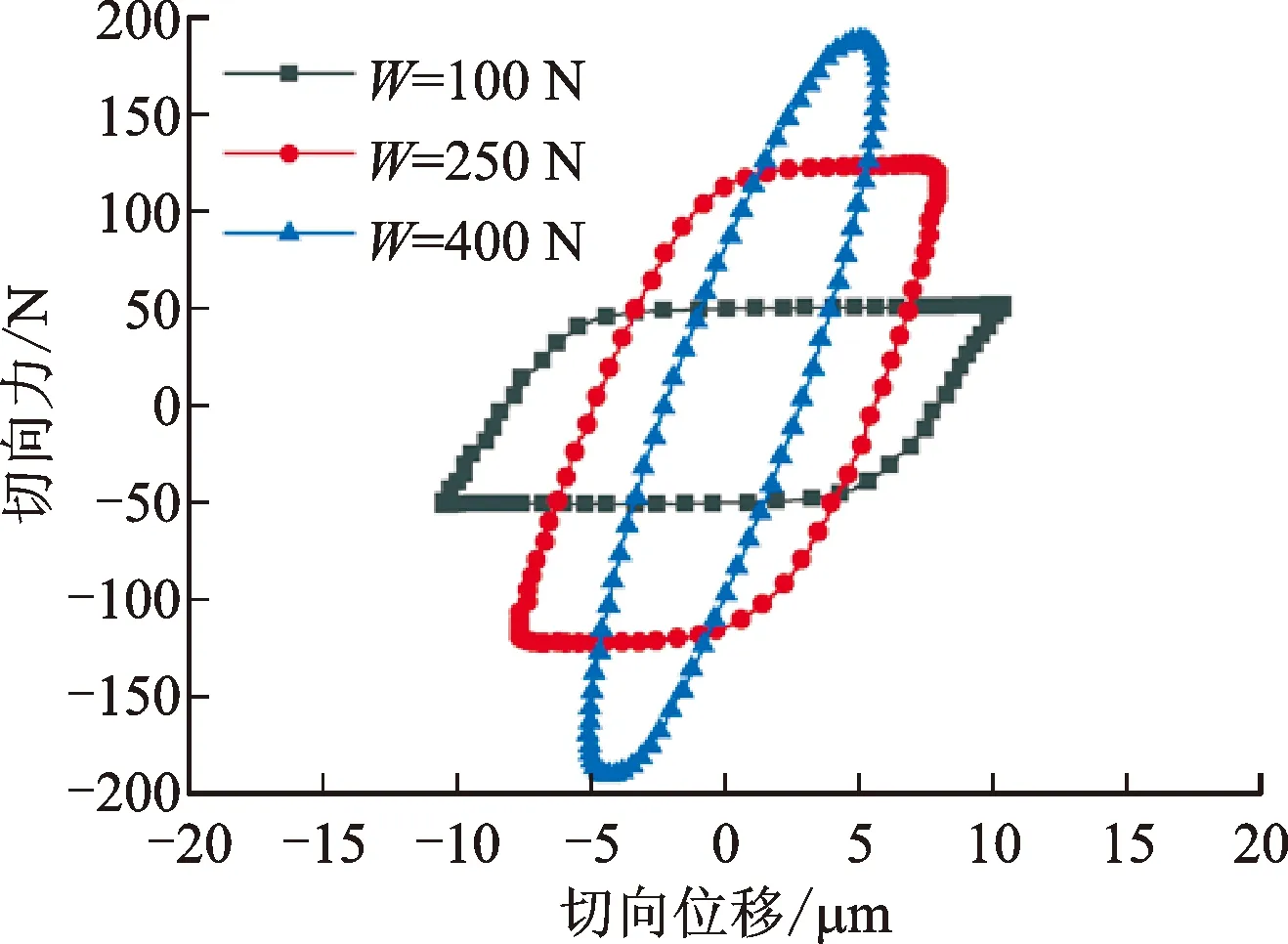
(a)Q235

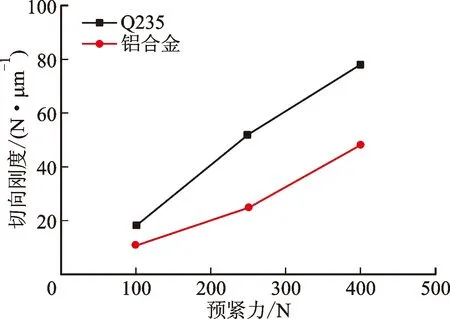
图8 当Δs=25 μm时不同预紧力下界面的切向刚度Fig.8 The Ttangential stiffness of the interface under different preloads (Δs=25 μm)

此外,微动响应很大程度受到激励振幅的影响。图9描绘了摩擦副在相同的预紧力(W=250 N)和不同振幅的正弦激励(Δs=10、15、20、25、30 μm)下的迟滞回线。从中可以观察到:摩擦副在受到小振幅的激励时,迟滞回线呈椭圆形,界面发生局部滑移,界面的最大切向力随激励幅值的增加而变大;当激励幅值增大到一定程度后,迟滞回线形状变成平行四边形,界面发生大滑移行为。对比图9a与图9b,界面发生大滑移行为之后,Q235摩擦副界面的最大切向力基本保持不变,而铝合金摩擦副界面的最大切向力会有小幅下降。产生这一现象的原因是:在循环切向载荷的作用下,关节界面的预紧力螺栓发生松动[16],但较软材料摩擦副的连接螺栓松动现象较明显。在相同的预紧力下,施加的激励幅值对关节界面的切向刚度没明显影响,如图10所示。

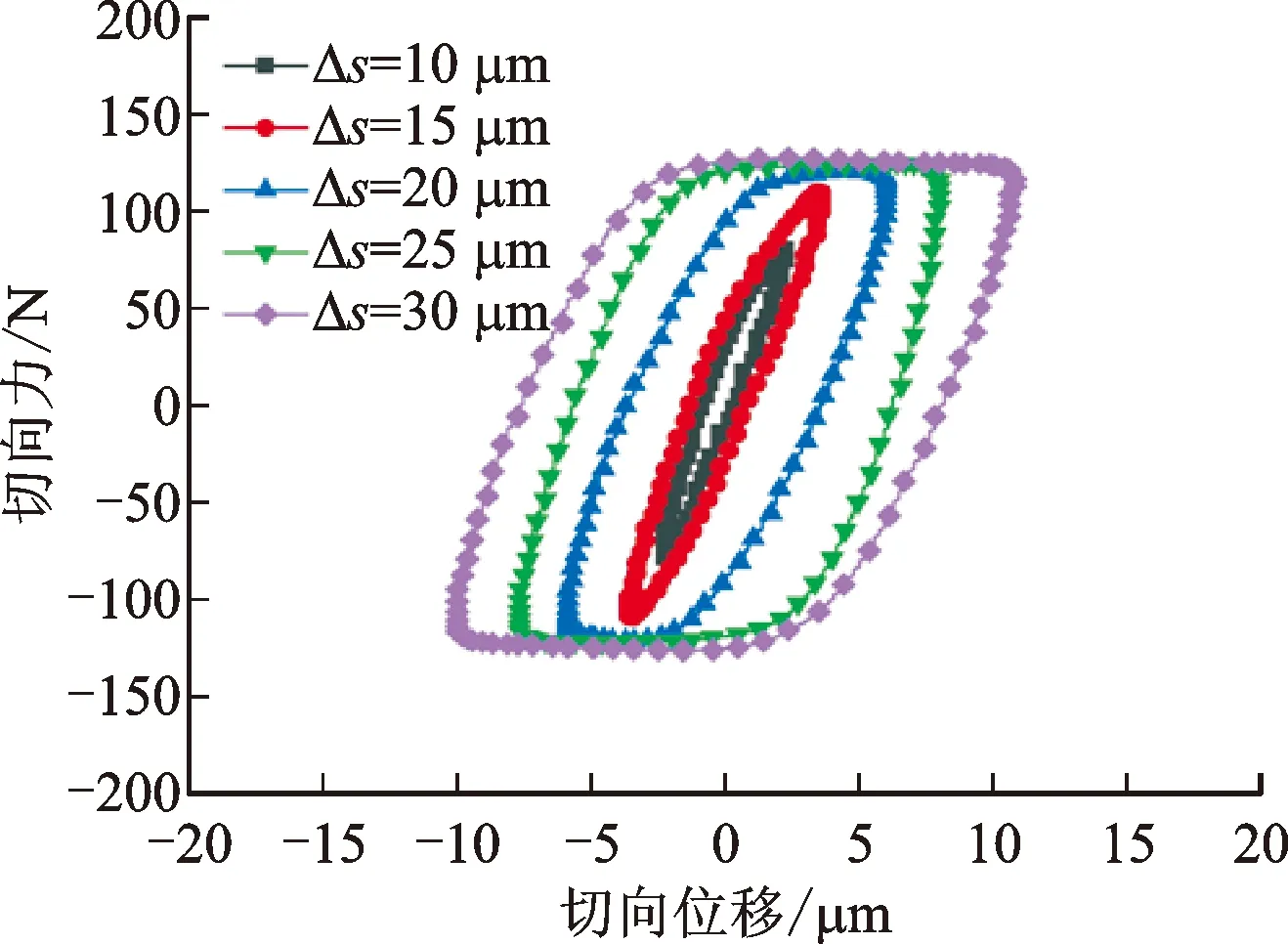
(a)Q235

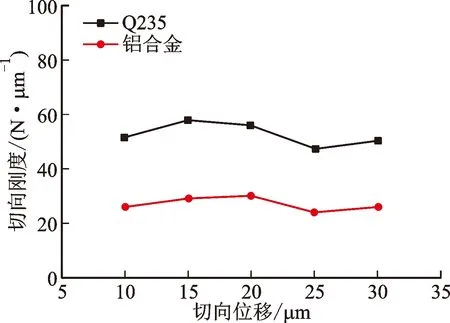
图10 当W=25 N时,不同激励幅值下界面的切向刚度 Fig.10 The tangential stiffness of the interface under different excitation amplitudes (W=25 N)

3 数值模拟与实验结果的对比

为了验证本文模型的有效性,将本文推导的滑移屈服力的分布函数(式(12))结合式(9),可推出界面切向运动的脊线方程F(x*)。在循环切向载荷的作用下,正、反向加载曲线可以利用脊线方程通过Masing准则[23]求出。在加载阶段,加载力-位移曲线方程具有以下形式

(13)

如果系统处于卸载阶段,那么卸载力-位移曲线方程可以表示为

Fu(x*)=-Fr(-x*)

(14)

式中:A为施加正弦激励的幅值。

不同工况下对摩擦副进行切向循环位移加载得到的迟滞曲线见图11。其中Q235摩擦副名义接触面积An=272.6 mm2,摩擦系数f=0.48,塑性指数ψ=2.77,σ/R=7.45×10-2,β=0.021;铝合金摩擦副名义接触面积An=272.6 mm2,摩擦系数f=0.3,塑性指数ψ=1.83,σ/R=4.71×10-2,β=0.003 74。从图中可以看出,在低预紧力时,理论计算值与实验结果吻合较好;当预紧力增大时,理论计算值与实验结果误差变大。原因可能是:当预紧力增大时,连接界面受到的切向力也变大,实验装置其他地方的变形会对实验仪器的测量结果有一定的影响;此外,本模型认为摩擦系数为定值[24],且未考虑摩擦副表面呈非高斯分布的情况[10]以及摩擦过程中表面形貌的变化[25]。

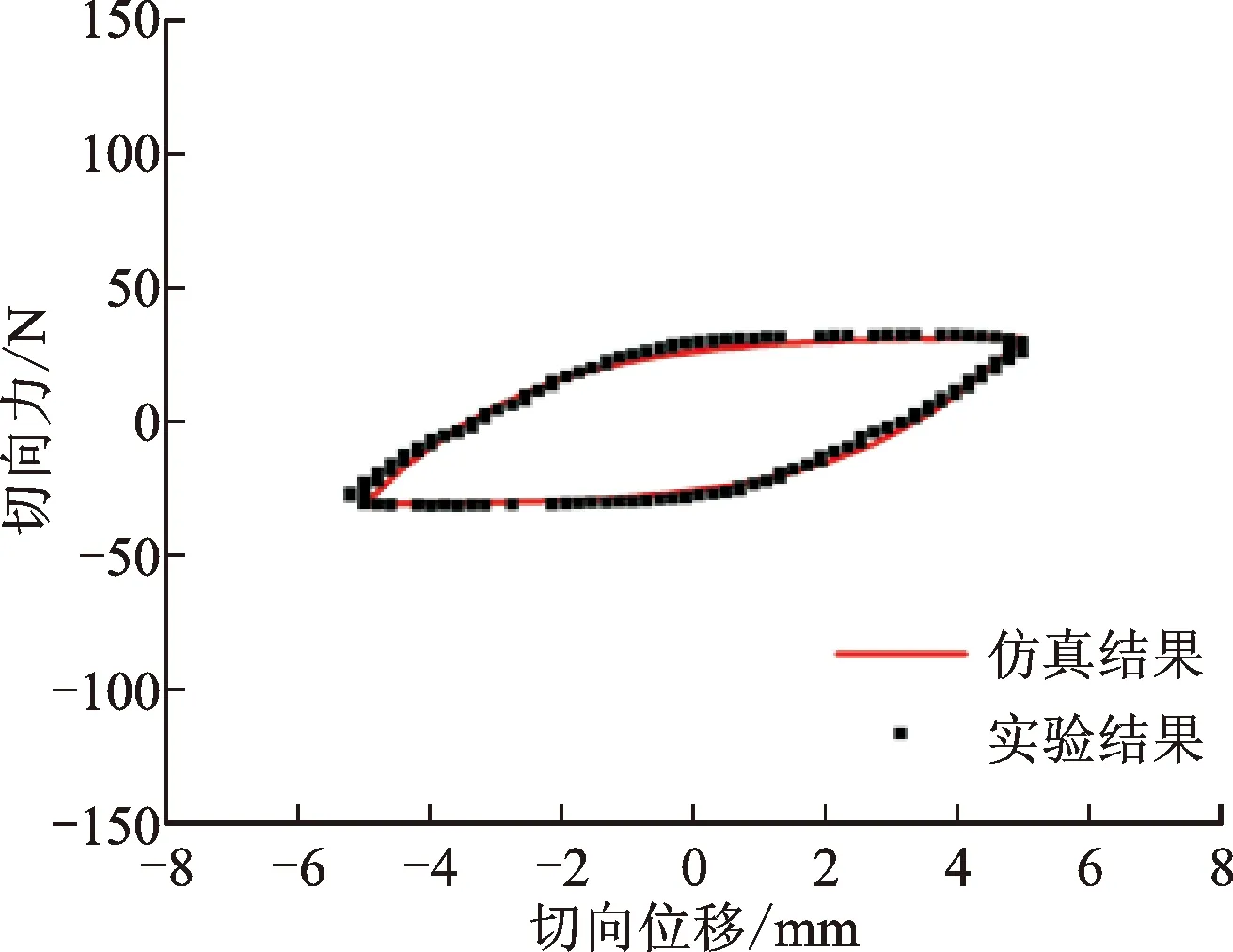
(a)W=100 N,铝合金

4 结 论

(1)本文通过将平行系列Iwan模型与关节表面粗糙峰的接触进行对比,用詹金斯单元来替代粗糙表面微凸体变形,建立了粗糙表面切向接触的微滑动模型。

(2)根据建立的切向模型,推导了Iwan模型中摩阻片临界屈服力的密度分布函数ρ(φ),并赋予ρ(φ)明确的物理意义。

(3)搭建一种高精度且易拆卸的微动装置,可以实现微米级微动环的测量。测试数据经过数个周期之后趋于稳定,预紧力和激励幅值对微动环的形状有较大影响。随预紧力的增加,关节界面处的切向刚度有很明显的增加,但激励幅值对切向刚度影响较小。