兼顾电压稳定和连锁故障触发的电网预防策略研究
邓慧琼,陈心耘,吴俊媛,马若涵
(福建工程学院电子电气与物理学院,福建福州 350118)
0 引言
电力网络是当今全球遍布面积最广、结构最复杂的人造系统之一。近年来频频发生的大面积停电事故充分暴露了大型互联电网脆弱性的一面[1]。大面积停电事故的发生常是由电网连锁故障所触发。
近几年来,针对电网连锁故障的研究者们提出了许多新角度的研究思路,为深入研究电网连锁故障提供了诸多有益的启示。如文献[2-4]着眼于目前国家大规模推广使用的新能源,研究风电接入电网后对于电网运行状态和电力调度的影响,但这些优化不适用于传统的电力系统,具有一定的局限性。文献[5-6]通过计算分析输电线路因故障造成的风险值,并评估输电线的相对脆弱性,对运行状态进行评估,据此建立预防模型。但是仅考虑输电线路的故障风险性过于简单,电网的系统故障错综复杂,应进行多方面的分析考虑。文献[7-9]提出电力系统的过载风险指标构建快速预防控制模型,提高控制模型的计算效率;或提出将CNN 和时域仿真结合,给出最优的控制方案;或以发电机组调整量最小为目标提出预防控制模型。也有的研究人员提出在预防连锁故障的发展过程中,以发电机的有功功率作为控制手段,考虑预防控制手段的时间要求,并以电网可承受的约束度和经济性最优作为优化目标[10-12]。文献[13]利用非线性最小化模型,根据PCRA 原理建立更新故障集,从而计算更新电压风险与对策,直到对预期的意外事件不再降低风险为止。更加创新的研究者将自组织临界理论与Mann-Kendall 检验方法[14]、复杂理论中的同配性概念[15]、熵理论[16]等相结合,分析辨识电网的自组织临界状态,从而判别预防电网发生连锁故障。
目前的这些研究比较注重电网连锁故障发展过程中的仿真模拟及其后果分析,但这些研究对连锁故障发展过程的模拟计算量很大,电网调度人员就无法快速做出反应,电网发生连锁故障时依旧无法控制;大部分研究缺少同时对连锁故障的安全裕度和对电网的电压稳定设定安全指标进行监控和优化;不管连锁故障是如何发展,究其根源仍旧是起始于最初的连锁动作。电网初始的扰动在很大程度上能够决定后面发生的一系列连锁故障的严重程度,因此,对其起始连锁动作的深入挖掘具有现实价值。
本文针对电网连锁故障的初期阶段表现——连锁跳闸,提出基于预防连锁跳闸的安全裕度指标和电网电压稳定指标的预防模型。首先对电网的连锁跳闸进行分析,提出能够预防连锁跳闸的安全裕度指标[17]。其次考虑了电网的电压稳定性,提出了针对电压稳定的局部电压稳定指标(L指标),通过分析计算出电网中所有负荷节点的L指标的值,将这些值进行大小排序,其中最小的值所对应的负荷节点即为电压稳定最脆弱的节点,应对其进行优化。因此,本文提出的预防模型通过调整发电机组出力,结合电网各种约束,以优化电网的电压稳定和安全裕度为目标函数,从而预防电网发生连锁故障,提高电网运行的稳定性。本文以IEEE39 电网系统为例,得出的仿真结果合理地验证了预防模型的可行性。
1 预防模型
1.1 电网安全裕度指标
采用电网某一时刻运行状态t0下的支路电流Iaf与电网临界状态下t1的支路电流Isf进行无量纲处理,两者之间的最短距离m(I)作为衡量电网是否会发生连锁跳闸的安全裕度指标。初始故障被切除后,剩余电网正常运行部分是否因某一条支路lst发生故障而出现连锁跳闸,式(1)定义的变量m(I)为:
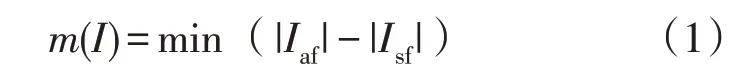
要实现电网处在运行状态t0且电网受到初始故障冲击后不会发生连锁跳闸的目标,则应对m(I)进行优化,可得:

式中:f为安全裕度指标。
f应不超出临界状态的范围,即:

保证f的值不小于0,即电网当前运行状态与临界状态之间的最短距离不小于0,电网不发生跳闸。
1.2 电网电压稳定指标
若只是单方面地从电网的节点注入功率入手预防连锁跳闸发生是不够全面的。即使电网的初始扰动被切除,电网依旧有可能因电压不稳定的节点没被发现,随着运行时间的增加,节点的电压不稳定性逐渐增大而导致电网再次出现扰动,触发连锁跳闸。因此本文借鉴文献[18~20]使用L指标(无量纲)作为评估电网节点的节点电压稳定性的安全指标。
L指标最初由Kessel[21]等人提出,由两节点系统导出。在大于两节点的系统中,将系统中的节点划分为两类:一类由全部PV节点组成,定义为TP;另一类由全部PQ节点组成,定义为TQ。
在电网中,建立节点导纳矩阵的节点网络方程:
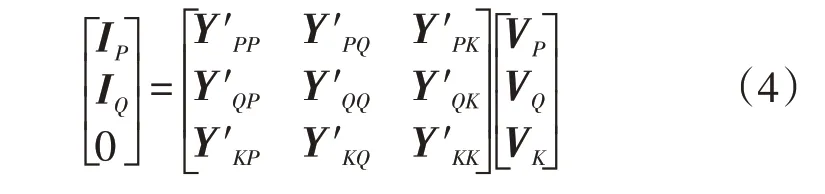
式中:VP,VQ,VK分别为为PV节点、PQ节点、平衡节点的电压向量;IP,IQ分别为PV节点、PQ节点的电流向量;分别为只包含PV节点、PQ节点、平衡节点的节点导纳子矩阵;分别表示PV节点与PQ节点、平衡节点具有关联性的节点导纳子矩阵,同理可得。
消去网络中的平衡节点,式(4)可变换为:
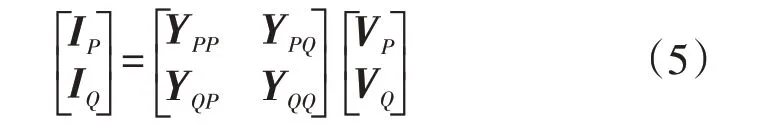
式中:YPP,YPQ,YQP,YQQ为消去平衡节点后,PV节点和PQ节点的节点导纳矩阵。
再由YPP=ZPP-1和YQQ=ZQQ-1式(5)转化为:
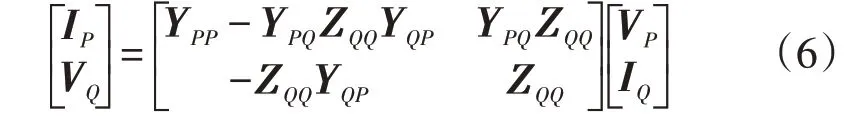
文献[21]定义PQ节点j的局部电压稳定指标Lj为:

式中:和分别为PQ节点的节点i和节点j的电压向量;为PQ节点j,i之间的共轭互阻抗矩阵;为电网对节点i的等值负荷。
由式(7)可知,在多节点系统中的某个PQ节点j,若该节点电压稳定,则其L指标的取值范围为0
因此,在式(7)中L指标取值越小,表示电网越稳定,L指标取值越接近于1,电网越不稳定。对于电网整体,将所有PQ节点计算出的L指标数值由小到大排序,其中L指标数值最大的节点即为电网中电压最不稳定的节点。因为在整个电网中,任何1 个PQ节点出现电压失稳的状况,都有可能造成电网出现故障,甚至发生连锁跳闸,所以本文取其中电压最不稳定节点Lm代表电网整体电压的稳定性并将对其进行优化,如式(8):

为了便于后续模型的优化,将式(7)的取值范围进行预处理,对式(8)进行转化,L′表示修改取值范围后的电压稳定指标:

此时L指标取值范围变为L<1,电网的节点电压稳定性提升时,L′越接近于1;当节点电压稳定性下降时,L′越接近于负无穷。
1.3 预防模型的建立
将电网的安全裕度指标和反映电压稳定的L指标相结合,可得预防电网连锁跳闸的目标函数。在电网运行中,若能优化调整电网的发电机组出力,在保证满足负荷需求的前提下,尽可能保证式(9)中的L′以及式(2)中的f得到最大的优化,则电网运行稳定越有保证,电网的连锁跳闸将得到有效预防。因此,将式(2)和式(9)整合成目标函数F:

式中:a1,a2为权重系数,a1=a2=0.5,待优化变量为发电机组出力。
由式(2)和式(9)可知两式皆为求得其所对应的的最大值,因此式(10)整合后的目标函数H为:

将式(11)的目标函数再加上电网所需的各类电气约束关系,可得完整的优化模型。
同时应考虑电气约束关系,其中包含电网切除初始故障前后的电网潮流约束,分别为T0和T1[22]:

在预防模型中不等式约束关系为:
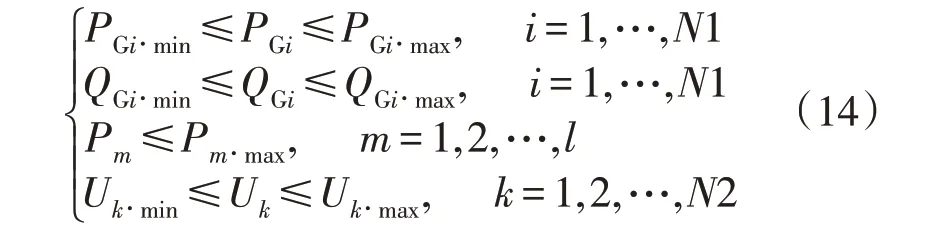
式中:PGi和PGi∙max、QGi∙min分别为为电网中第i台发电机的有功出力与其有功出力的上下限;QGi和PGi∙max,QGi∙min为电网中第i台发电机的无功出力与其无功出力的上下限;Pm为支路lm传输的有功功率;Pm∙max为支路lm传输的有功功率最大值;Uk∙min与Uk∙max分别为节点电压Uk的最大值和最小值。
将式(14)写成缩略形式,可表示成式(15)的形式,式中M0(x)包含式(14)所有不等式的约束关系:

综合式(3)和式(11)—式(15),可得出通过调整发电机组出力,使得电网安全裕度和电压稳定得到优化的预防模型为:
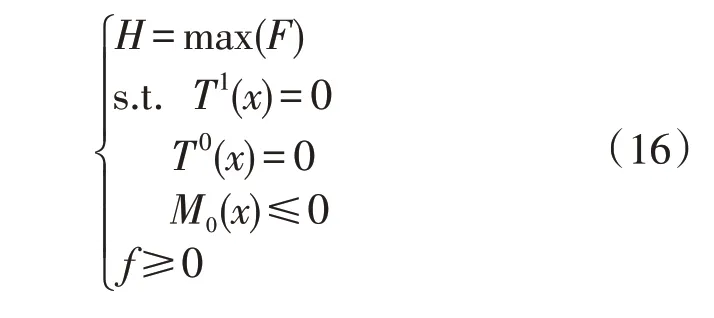
2 预防模型计算流程
本文采用粒子群优化(Particle Swarm Optimization,PSO)算法对预防模型进行求解。PSO 算法相对于常规算法而言,具有收敛性好、计算速度快、不受问题维数限制等优点[23],而且PSO 算法还具有原理简单,易于实现优化目标等优点[24]。
为了使得PSO 算法能够服务于该预防模型,本文应先对式(16)所示的优化问题进行适当的简化:
1)针对式(16)中的各项潮流约束,采用潮流计算进行迭代计算处理,若潮流约束得不到满足,则粒子群中将产生新的粒子进行替代,使计算符合潮流约束。
2)为了使粒子群算法更好地处理式(16)中的预防模型,将其目标函数转变为式(17)所示的惩罚函数HH形式。
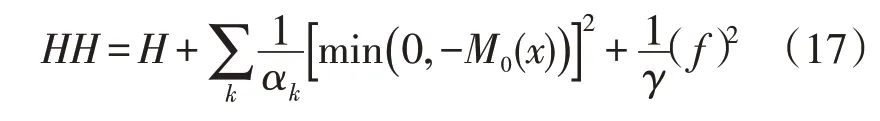
式中:αk,γ均为惩罚因子。
具体算法流程图如图1 所示。
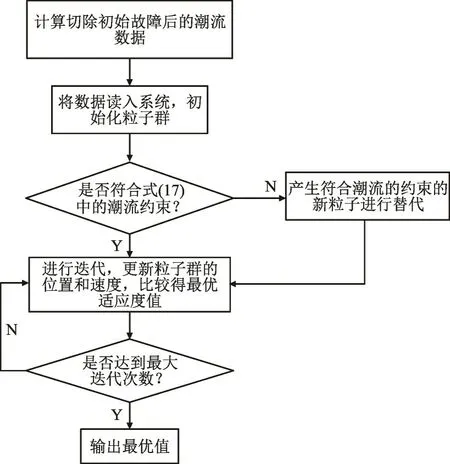
图1 算法流程图Fig.1 Flow chart of algorithm
3 算例分析
以图2 所示的IEEE39 节点系统为例,在Matlab环境中进行编程,电网的基准容量为100 MVA,设定虚拟电流型后备保护整定值为5.77 kA[25]。

图2 IEEE39节点系统接线图Fig.2 Wiring diagram for IEEE 39-node system
本文设IEEE39 节点系统中的第10 条支路l10为初始故障支路,在切除这条初始故障支路后,利用粒子群优化算法搜索电网当前最接近连锁跳闸临界状态的运行状态,计算两者之间的最短距离,大小由m(I)表示。另一方面,算法同时搜索电压最不稳定节点,提取其L指标的值进行优化。
由图3 可以看出,在粒子群优化算法300 次优化迭代过程中,图3 中曲线呈上升趋势,当粒子群算法迭代至第80 次后曲线趋于平缓。本文通过优化发电机组出力,最终将f值从0.016 优化至5.981,此后数值不再上升,可知已达到优化极限值。此时,电网当前运行状态t0与电网发生连锁跳闸状态t1之间的距离得到有效增加,极大地降低了电网发生连锁跳闸的可能性,提高了电网的安全裕度。
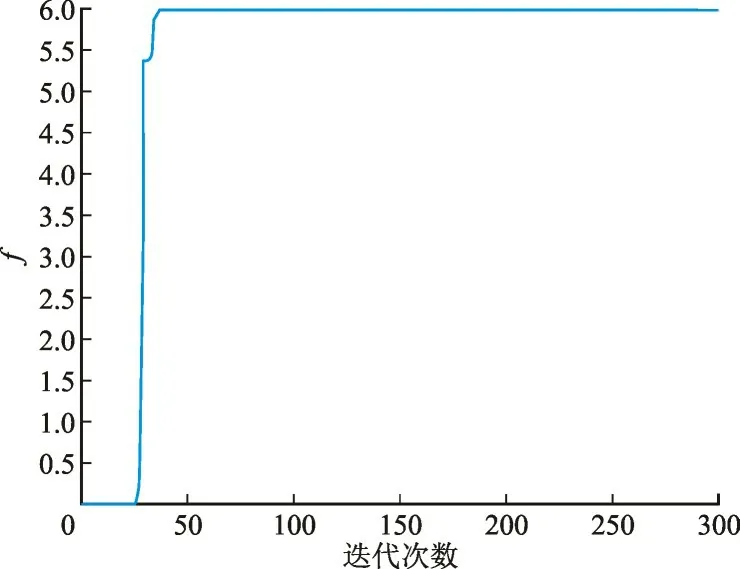
图3 安全裕度指标f优化图Fig.3 Diagram showing optimization of f
由表1 可知,去除初始故障后,将求出的剩余节点的L指标数值从大到小排序,得第5 节点的L指标为最小,L5=0.719 1。可判定第5 节点为电压最不稳定节点,有极大可能性导致连锁跳闸发生,需对该节点进行优化,提高第5 节点电压稳定性。

表1 计算电网PQ节点的L′指标值Table 1 Calculation of L′for PQ node in power grid
在表1 的基础上,可知此时图4 优化的是第5节点的L指标。从图4 可以看出,算法一共迭代300 次,在第80 次后L′的数值不再变化,L′从0.719 1 优化至0.872 5,减小了第5 节点发生电压失稳的可能性。

图4 L指标优化图Fig.4 Diagram showing optimization of L
因此本文提出的预防模型能够有效地提高电网安全裕度和电网整体的电压稳定,进而提高了电网运行的安全性和稳定性。图5 的拟合曲线十分直观地证明f与L′之间的正相关性,即在优化过程中,电网的安全裕度指标和L指标相互之间为积极影响,不会出现冲突或者相互制约的情况。

图5 f与L′关系图Fig.5 Relationship between f and L′
在表2 的最优发电机组出力数据的基础上,随机修改最优发电机组出力数据,计算在这些数据下的电网安全裕度指标和L指标的数值,并与图3 和图4 的数据进行对比。
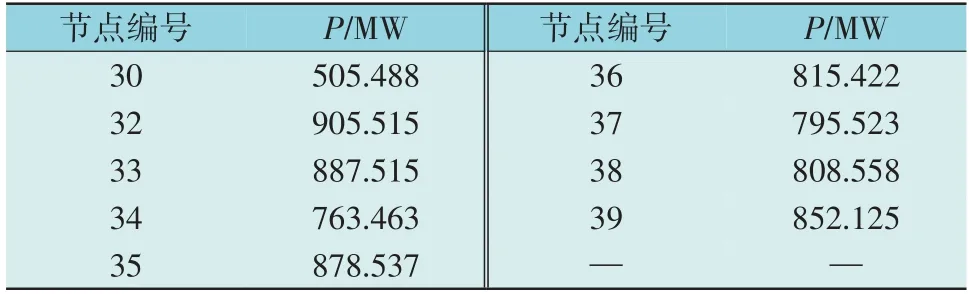
表2 最优发电机组出力Table 2 Optimal generator output
图6 中共有400 个不同的发电机组出力状态配置。由图6 所示可知,图中最优的f值为5.972,小于图3 中的最优f值5.981。由图7 可知,在这些配置下,第5 节点的电压稳定只能优化至0.871,小于图4 中的最优L′值0.872 5。
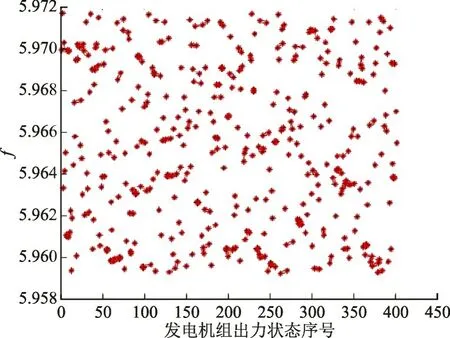
图6 各发电机组出力状态下安全裕度指标f值Fig.6 Value of f under output of each generating set
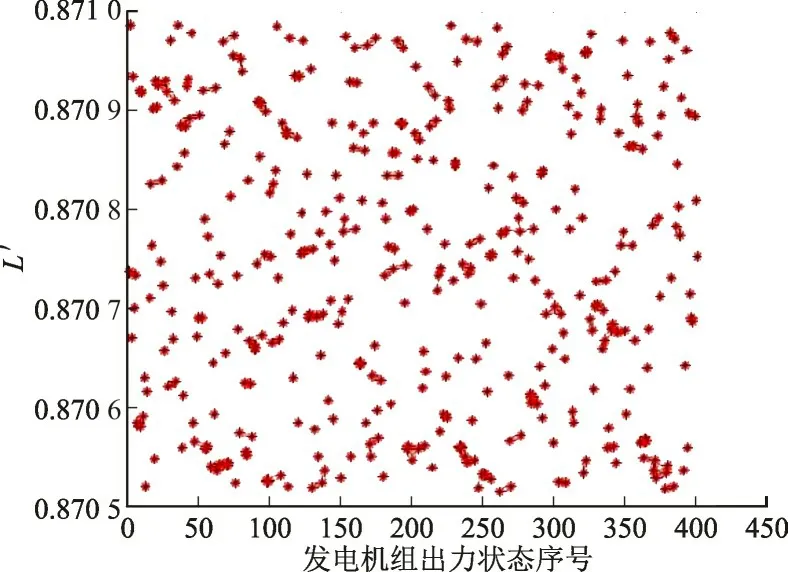
图7 各发电机组出力状态下L指标值Fig.7 Value of L under output of each generator set
综上所述,本文提出的预防模型求解思路合理,能够通过分析计算得到最优发电机组出力状态配置,使电网具有最优的安全裕度和电压稳定性。
4 结论
针对预防电网发生连锁跳闸的预防模型,通过提高电网运行时的安全裕度和电网电压稳定性,达到多方面预防连锁跳闸的研究成果。
1)本文提出利用电网安全裕度指标和L指标,建立了一种完整的用于预防的优化模型,使得其影响程度有了明确的物理意义。
2)通过粒子群优化算法在IEEE39 节点系统中仿真,所得曲线图证明本文提出的预防模型是合理有效的。
3)本文提出的预防方法可为研究人员进一步研究分析电网复杂的运行状态提供新思路和借鉴。

