基于运行可靠性的风电容量可信度研究

单维康，林超凡，石文辉，谢海鹏

（1.西安交通大学电气工程学院，陕西西安 710049；2.中国电力科学研究院有限公司，北京 100192）

0 引言

面对全球气候的不断变化，许多国家和地区先后提出了“碳中和”和“碳达峰”的目标[1-2]。2020 年9 月22 日，习近平总书记在第75 届联合国大会一般性辩论上提出，中国将采取更加有力的政策和措施，二氧化碳排放力争于2030 年前达到峰值，努力争取2060 年前实现碳中和。“双碳”目标要求构建以新能源为主体的新型电力系统，这不仅为未来电网发展指明了方向，也开辟了中国特色能源发展新道路[3]。

能源行业特别是电力系统的低碳转型发展对“双碳”目标的实现尤为重要，能源供给清洁化的要求使得新能源发电亟需创新发展和技术升级。未来，高比例新能源接入系统带来的波动性和随机性将对电力系统维持发电和负荷的实时电力平衡带来巨大挑战，对电力系统规划和运行产生深远影响[4]。以风电为例，由于风电出力的不确定性，通常情况下相同容量的风力发电机组与常规发电机组带负荷能力并不相同[5]，调度计划中对风电带负荷能力的估计不足可能使风电消纳困难，系统的运行成本也有所增加。风电可信容量（Credible Capacity，CC）能够反映风电对常规机组的替代程度，使风电能够与常规机组在相同意义下进行研究。

当前，国内外已针对风电容量可信度开展了大量研究，在风电的预测及出力建模、容量可信度计算方法等方面都取得了一些成果。在风电场出力建模研究方面，文献[6]提出采用正则藤Copula 函数对多风电场之间的空间相关性建模，在多种预测条件下形成条件预测分布，提高了预测的质量。由于大规模风电的接入，它们的不确定性可能存在多维依赖关系，导致对电力系统的分析面临着“维数灾难”，文献[7]通过高维Copula 理论和离散卷积的方法进行高维相关离散计算，有效对解决了高维依赖计算带来的“维数灾难”。为定量描述风电功率波动概率分布，杜刚等人[8]在不同时空尺度下采用不同分布形式对其拟合，得出重尾分布更适合描述风电功率概率分布的结论。

在风电的容量可信度研究方面，Garver 最早在上世纪提出了容量可信度概念[9]，研究不同停运率的常规机组载荷能力的差异。文献[10]采用优化模型，基于系统失负荷期望指标（Loss of Load Expectation，LOLE），对风电接入前后的系统可靠性进行分析，将风电场近似等效为具有一定容量的火电机组。文献[11]提出基于Hadoop 架构的大数据技术计算风电容量可信度，引入机架感知配置法和Hush Bucket 存储算法对其进行改进，提高了数据存储及数据处理的效率，减少计算时间。针对计算风电容量可信度的准确度和计算速度不能兼容的问题，文献[12]提出了最大公因子步长算法，通过负载-失负荷概率曲线，能够在保证计算效率的同时准确计算风电的容量可信度。为了聚焦发电侧和用户侧的相互作用关系，文献[13]提出考虑瞬时响应和负荷恢复过程中不确定性的复合可靠性模型，从需求响应的角度研究了分布式发电的容量可信度。

然而，现有研究对风电容量可信度的研究大多是集中于电力系统规划层面，对运行层面风电容量可信度的研究并不深入。为此，本文围绕运行层面下的风电容量可信度开展研究：（1）提出了基于Copula 和条件概率的风电预测误差概率建模方法；（2）提出了基于等效容量的运行可靠性评估方法；（3）提出了风电运行容量可信度在线评估框架；（4）通过算例研究了不同时段风电运行容量可信度，得到影响可信度的关键因素，分析其对调度计划的影响。

1 发电机组等效容量

1.1 风电场等效容量

研究运行层面上的风电容量可信度需要考虑风电各时刻的出力不确定性，该不确定性由风电预测出力和预测误差两部分叠加而成。风电预测可以通过单步或多步预测得到[14-15]，相关的算法已比较成熟，本文不再赘述。由于造成风电场容量“不可信”的重要因素为风电的预测误差，因此本文首先对其进行概率建模，继而形成风电场的等效容量。

1.1.1 风电预测误差条件概率分布建模

考虑到风电预测误差会随预测出力的变化而变化，为提高对风电预测误差建模的精度，本节采用Copula 模型研究风电预测误差与预测出力之间的相关性，针对各时刻风电预测出力情况建立不同时刻下预测误差的条件概率分布模型。

在Copula 理论中，假设x和y为随机变量，它们的可逆累积分布函数分别为FX(x)和FY(y)的随机变量，且都服从均匀分布，即：

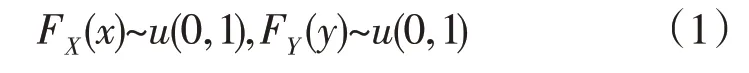
它们的联合分布函数FXY(x,y)可以通过Copula函数[16]写为：

式中：C(FX(x),FY(y))为相应的Copula 函数。

利用Copula 函数对风电实际出力及预测出力建模时，设x为实际出力，y为预测出力，实际出力和预测出力联合概率密度函数fXY(x,y)为：

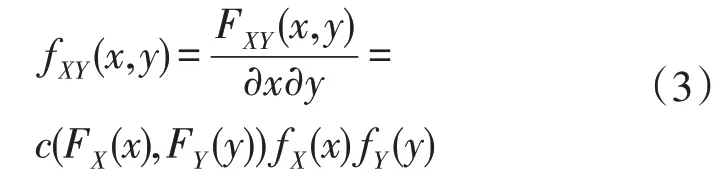
式中：c(FX(x),FY(y))为Copula 概率密度函数；fX(x)，fY(y)分别为x和y的边缘概率密度函数。

当已知风电在某点的预测功率为y=[17]，可以得到在该点下风电实际出力的条件概率密度函数如式（4）所示：

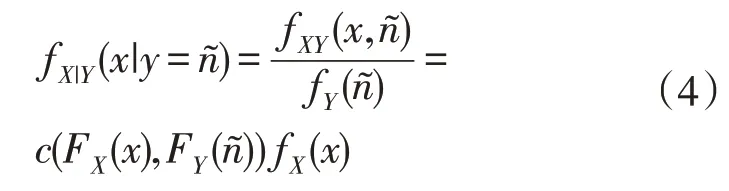
对于预测误差s=x-y，其建模可以由式（4）类推，即条件概率密度函数为：

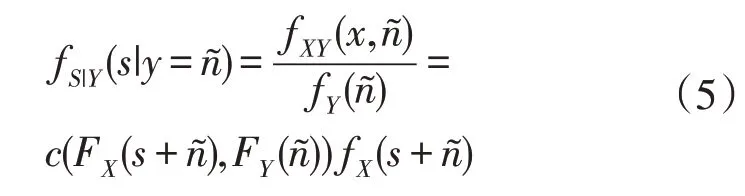
若系统中存在m个风电场，则它们的联合累积分布函数为：

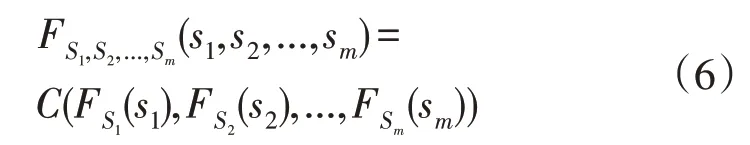
当同时考虑m个风电场之间的条件相关性时，它们的联合条件概率密度函数为：

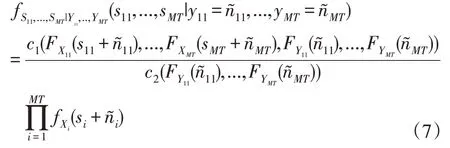
单个风电场的条件概率分布可以被扩展为：

1.1.2 基于风电预测误差的出力建模

本节分别在各时段根据不同的预测误差分布情况形成离散的概率分布，分别选择预测出力的80%,90%,100%,110%,120%形成风电的五状态模型，便于与后文常规机组等效容量模型卷积。风电等效容量为：

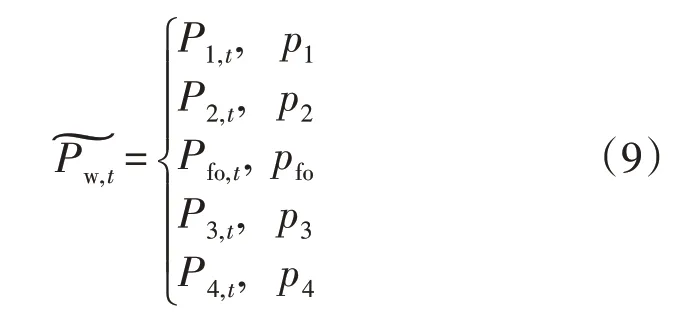
1.2 常规机组等效容量

在风电运行容量可信度的计算中，常规机组等效容量模型采用两状态模型，即考虑机组随机停运率的等效容量，如式（10）所示：

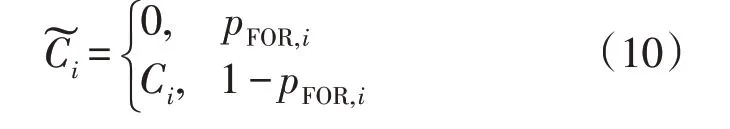
常规发电机组等效容量分布利用卷积计算方法获取，不同时刻下常规机组开机方式不同，其等效容量分布也不同。若在运行阶段t时刻某一开机方式下，共有i台常规机组处于开机状态，通过卷积法[18]可以得到此时加载i台常规机组的等效容量分布，如式（11）所示：

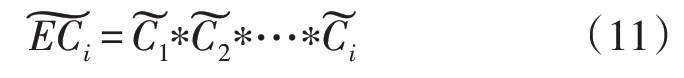
1.3 系统等效容量

得到风电场和常规机组的等效容量后，根据各时刻系统的开机方式组合，得到不同时刻下系统的等效容量分布情况。若系统在t时刻安排m台常规机组和n个风电场出力，则等效容量分布为：

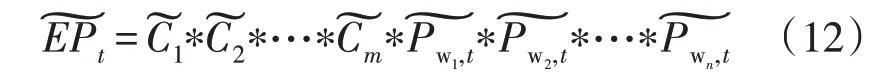
式（12）计算得到的等效容量分布是离散值，可以利用半不变量法[19]进行卷积计算，并通过Edgworth 级数展开得到等效容量的连续概率分布。

2 基于等效容量的运行可靠性评估

由于运行层面下的风电容量可信度与系统各运行时刻的可靠性水平密切相关，可靠性水平随时间波动，因此本章研究运行可靠性评估的相关理论，为研究风电运行容量可信度提供支撑。

本文采用时序的负荷序列：

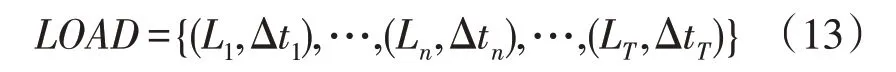
式中：(Ln,Δtn)为n时刻的负荷水平以及持续时间；T为研究周期总时长。

根据1.3 所述的系统等效容量模型，系统中加载不同数量的机组时等效容量分布曲线不同，示意图如图1 所示，F（x）为等效容量分布曲线，图1 中上半部分为不同情况下的等效容量分布情况，下半部分表示时序的负荷信息，L1，L2，Lt为不同时刻的负荷水平。

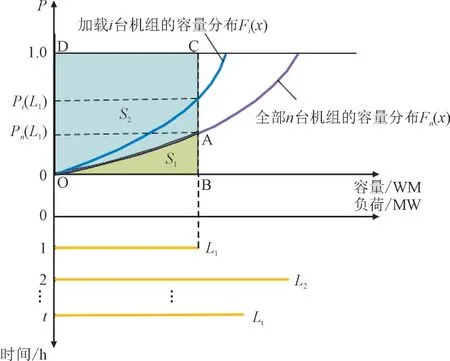
图1 等效容量分布曲线Fig.1 Curves of available capacity distribution

2.1 电力不足概率计算

图1 中Fi（x）和Fn（x）分别表示系统加载i台和n台机组后的等效容量分布情况，当系统某时刻的负荷水平为L1时，Pi（n）（L1）表示i（n）台机组在该负荷水平下发电容量小于L1的概率，也即i（n）台机组在该时刻下的电力不足概率（Loss of Load Probability，LOLP），如式（14）所示：

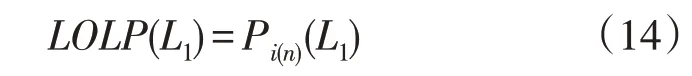
同时，由于第i+1 台机组在第i台机组不能满足负荷需求的情况下才会被加载，因此Pi（L1）也是在负荷水平为L1时第i+1 台机组需要被加载的概率。

2.2 电量期望值计算

根据分布曲线可知，系统加载了n台机组后电量不足期望值（Expected Energy Not Served，EENS）为等效容量分布曲线在横轴上的积分，几何意义上反映为图中S1的面积。即：

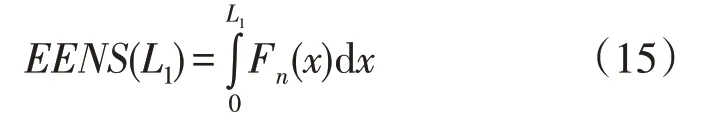
EENS 反映了某时刻下系统的电量不足期望值，而在电力系统负荷水平为L1时，n台机组在一段时间内应提供的电量为L1×Δt，因此在单位时间内，n台机组实际的电量期望值（Expected Electricity，EE）为图中S2部分所示面积，如式（16）所示：

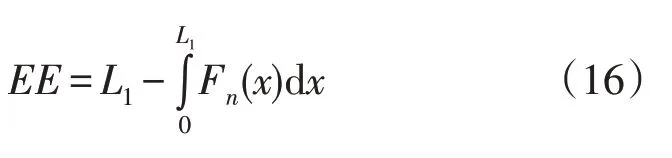
3 风电容量可信度评估

目前在电力系统规划中对容量可信度的定义通常有以下4 种方式[20-21]：（1）等可靠容量比例，即风电可以替换完全可靠的常规机组容量比例；（2）等常规机组容量比例，即风电可以替换具有一定停运率的常规机组容量比例；（3）置信度下的可靠出力，即定义发电侧的可靠出力为某置信度下机组可用容量大小，风电容量可信度为风电接入后该可靠出力的增量；（4）等效负荷承载力，即风电接入前后能够供应的负荷差值占风电装机容量的比例。

系统规划中对风电容量可信度的第（2）种定义一方面考虑了常规机组的随机停运率，另一方面考虑了负荷的不确定性，反映了含风电系统运行的真实情况，衡量了风电加入系统后对降低失负荷损失的贡献，因此本文基于运行可靠性不变的条件，在定义（2）的基础上提出运行容量可信度的定义：每小时系统可靠性不变时，风电替换的具有停运率的常规机组容量大小占该时刻下风电预测出力的比例。可以看出，风电的运行容量可信度是随时间波动的，这样在日前发电计划中将风电的出力按照其运行容量可信度安排，可以减少弃风率，更加合理地安排常规机组发电计划。

3.1 评估方法

在风电运行容量可信度的评估过程中，需要不断地向未接入风电的系统中加入一定容量的常规机组，反复试探不同的容量水平，使各个时刻的系统可靠性指标与风电接入系统时的可靠性指标在一定精度条件下保持一致。

采用弦截搜索算法评估风电的运行容量可信度，示意图如图2 所示，横坐标为添加的常规机组容量，纵坐标R为可靠性指标LOLP，随新增机组容量的增大而减小。图2 中Rset为风电场接入情况下某时刻的可靠性指标值，即搜索的目标值；R0为未新增常规机组时的可靠性指标；Pmax为常规机组最大新增容量。

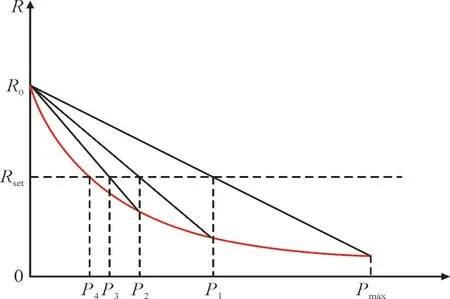
图2 截弦法示意图Fig.2 Schematic diagram of secant method for searching operation capacity credit

本文中弦截法的搜索过程为：（1）在某时刻下，首先取新增机组容量下限为0，上限Pmax为风电场装机容量，分别计算此时两个容量下系统的可靠性指标；（2）进而作两点间曲线的割线，与Rset相交后得到对应的容量P1，计算新增容量为P1时系统的可靠性指标；（3）重复迭代计算，新增容量由P2，P3依次逼近最终值。若在容量为P4时收敛，此时系统可靠性指标与接入风电时相等，则装机容量为P4的常规机组能够等效替换该时刻下的风电出力，风电可信容量为P4。

3.2 评估流程

基于对风电运行容量可信度的定义，利用系统的等效容量分布曲线获得原系统各时刻的运行可靠性指标，通过弦截搜索算法计算每小时风电的可信容量，具体流程为：

1）基于Copula 函数对每小时风电出力的预测误差建模，得到研究周期内各时刻预测误差的分布情况，进一步建立运行阶段各时刻风电出力的离散概率模型；

2）建立常规机组两状态模型，基于时序负荷信息，安排常规机组的开机方式，生成不同时刻下常规机组等效容量分布曲线；

3）考虑风电接入，获得含风电系统的等效容量分布曲线，计算此时系统的运行可靠性指标作为基准值；

4）去除风电，采用弦截搜索算法，在系统中反复增加或减少一定容量的常规机组，使系统运行可靠性指标较风电加入时保持不变，得到系统各时刻风电的可信容量，进而确定各时刻风电运行容量可信度。

4 算例分析

4.1 风电场预测误差分布研究

采用北方某省份2 个风电场2020 年预测和实际历史出力数据，利用阿基米德Copula 函数中的Gumbel Copula 函数形式对风电场预测误差条件概率建模，研究周期取为11 月份连续的168 h（7 d）。

图3 展示了该风电场的预测出力和实际出力数据的二维散点图，直方图刻画了实际出力和预测出力的边缘分布。

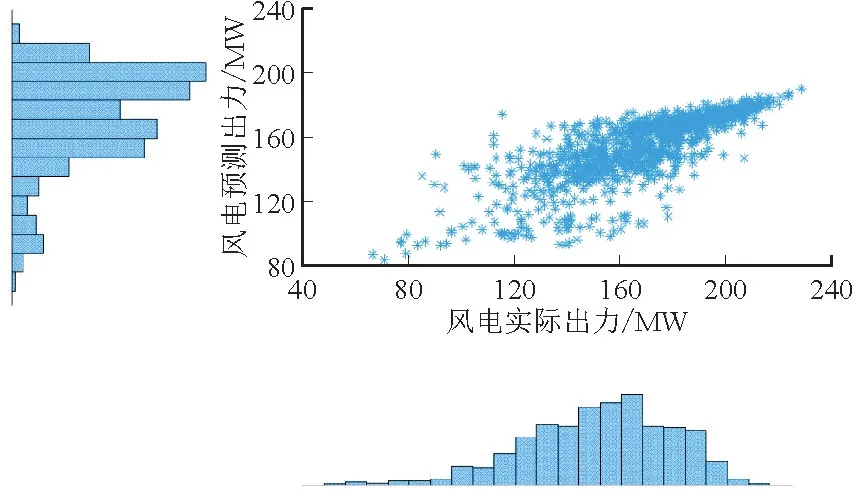
图3 预测出力和实际出力联合分布散点图Fig.3 Scatter plot of joint distribution of actual wind power output and its forecasts

图4 展示了风电场一周内各时刻预测误差条件概率分布情况，其中图例中不同颜色百分比对应了不同情况下的置信区间（Confidence Interval，CI）。从图4 中可以看出，预测误差的条件概率分布与预测出力的大小密切相关。当风电的预测出力相对较高或较低时，例如图中0～30 h，100～130 h，160～168 h 时段，预测误差通常对应较大的置信区间概率，即预测的不确定性很小，预测较为可信；当预测风电的出力值介于中间时，例如图中30～100 h时段，预测误差通常对应较小的置信度区间概率，即预测的不确定性很大。

图4 一周内风电预测出力及误差分布图Fig.4 Wind power forecast output with its error distribution in a week

4.2 风电运行容量可信度研究

根据本文所提方法，采用加入风电的IEEE RTS-24 节点系统进行算例研究，系统中常规机组单机容量分布在12～400 MW 之间，总装机容量为3 405 MW，系统详细参数见文献[22]，风电场装机容量240 MW。算例分别研究了典型日以及不同季节的风电运行容量可信度。

4.2.1 典型日风电运行容量可信度分析

利用本文所提方法，在运行可靠性不变的前提下计算某典型日风电的运行容量可信度，该日的风电和负荷曲线如图5 所示。

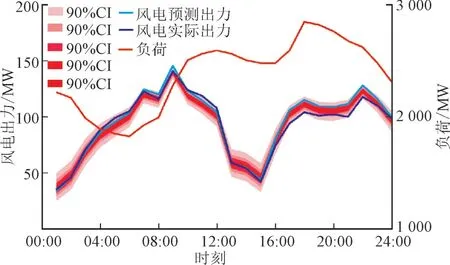
图5 典型日风电出力及负荷曲线图Fig.5 Curves of wind power output and load on a typical day

图6 为风电运行容量可信度及其可信容量的计算结果。不难看出，不同时刻下不同容量的风电能够在等可靠性的前提下替换常规机组出力，替换容量随时间明显变化。同时，在负荷水平相近时段，例如10 点与14 点，11 点与13 点，15 点、16 点与23 点，风电出力大的时刻，替换的常规机组容量也较大，风电出力较小时替换的常规机组容量也较小，风电运行可信容量与该时刻下风电出力的大小基本呈正相关。

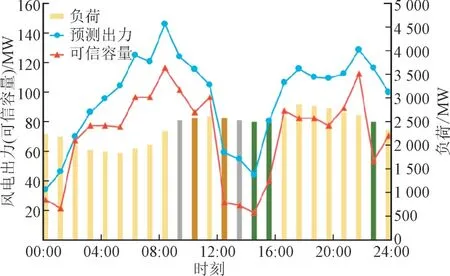
图6 各时刻风电可信容量对比图Fig.6 Comparison of wind power credible capacity at a different time

图7 反映了风电可信容量和容量可信度之间的关系。结合图6 的风电出力情况来看，风电的容量可信度在风机的出力较大时段（大于100 MW 时）普遍较大，在风机的出力较小时段相对降低，在22点时，风电容量可信度达到最大。将可信容量和容量可信度对比不难看出，在该日16 点与23 点负荷相同时刻，23 点的风电出力较大，可信容量也较大，但23 点的容量可信度比16 点时小，可见可信容量和容量可信度在每时刻的变化规律并不一致。

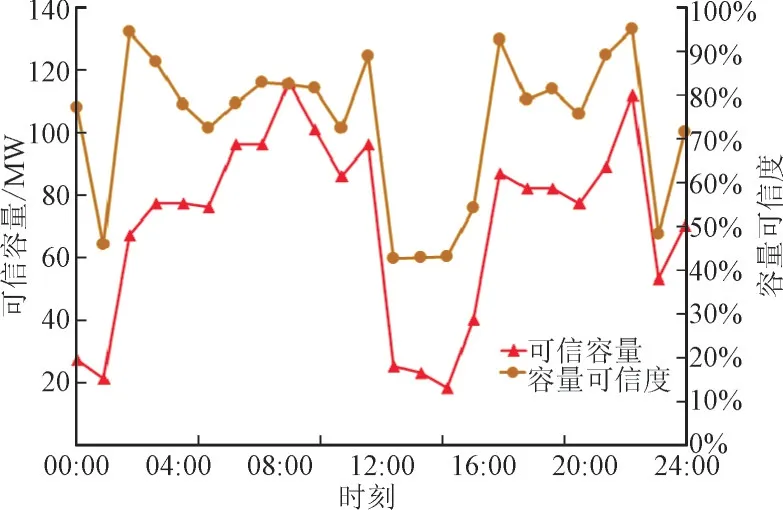
图7 运行时刻可信容量与容量可信度对比图Fig.7 Comparison of credible capacity and capacity credit

4.2.2 季节性风电运行容量可信度分析

在典型日风电运行容量可信度的基础上，本文在每个季节选择典型月份（30 d）的风电和负荷数据，组成120 d 的时序序列，其中风电各时刻出力曲线如图8 所示，每个季节的日平均负荷如图9 所示。

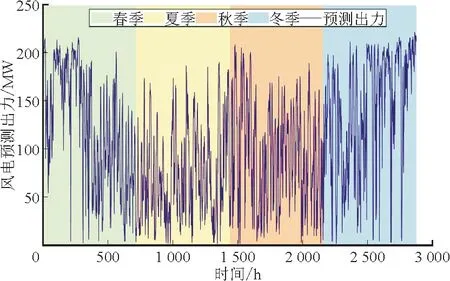
图8 风电各季节时序出力图Fig.8 Sequential wind power output in different seasons

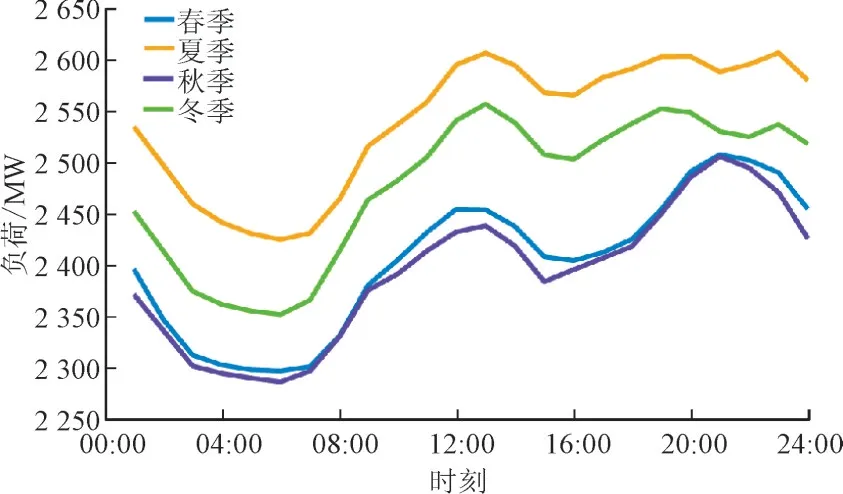
图9 不同季节日平均负荷Fig.9 Daily average load in different seasons

对各季节典型月份的风电运行容量可信度计算结果如图10 所示，横轴为120 d，纵轴为24 h，颜色越深的方格表示越高的容量可信度，即更大容量的常规机组可以在该时刻下被风电出力替换。从图10 可以看出，夏季和秋季很多时刻的风电容量可信度很小，甚至接近于0，春季的容量可信度值比较分散，有可信度大于80%的时刻，但也存在可信度为0 的极端情况，冬季的颜色较为均衡，容量可信度普遍在40%以上，容量可信度为0 的时刻很少，而该月的前22 d 还存在一个明显的特征，即夜间至凌晨的风电容量可信度较大，白天的风电容量可信度相对较低，这与冬季夜间风电出力较大相关。

图10 各季节风电运行容量可信度对比图Fig.10 Comparison of wind power capacity credit in different seasons

对比图8、图9 和图10 的结果，夏季的负荷较大而风电出力较小，风电的运行容量可信度水平较为离散，均值为全年最低，而全天容量可信度较高的时刻基本为负荷与风电都较大的时段；冬季的负荷较小，但是风电出力为全年最大，其运行容量可信度的均值为全年最高。由此可见，影响风电运行容量可信度的一个重要因素为风电出力大小与负荷的相关性，在本例风电渗透率10%的条件下，系统的净负荷主要取决于系统负荷本身，在系统负荷较大的时段，若风电的出力较高，则该时段的风电运行容量可信度也较大。

4.2.3 运行容量可信度对一周调度计划的影响

在目前调度计划安排中，风电的出力通常考虑取其预测出力减去20%的装机容量来进行安排，这时常低估了风电的可信容量，挤占了风电的消纳空间。本节选取11 月份中一周的风电各时段的可信容量与现有计划安排时考虑的风电容量对比，结果如图11 所示，其中风电装机容量为240 MW，“传统考虑容量”取值如式（17）所示：

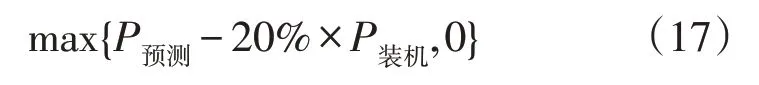
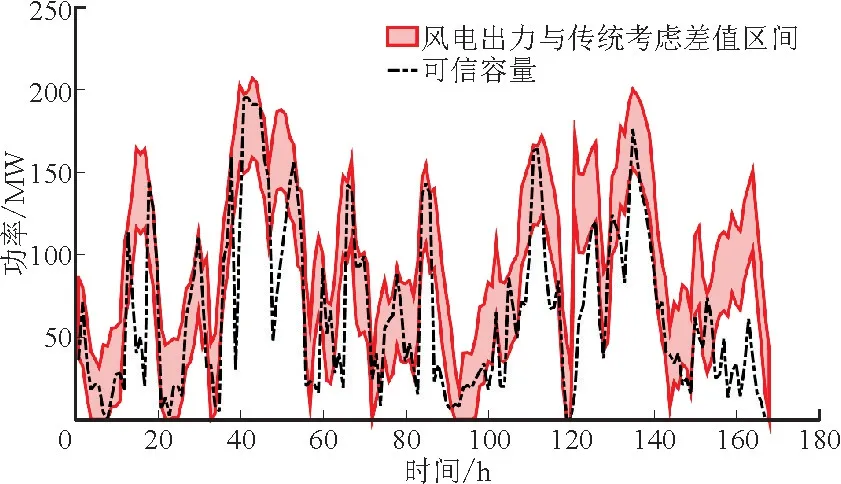
图11 目前调度计划考虑的风电容量与实际可信容量计算结果对比（一周）Fig.11 Comparison of calculations between considering wind power capacity in current dispatch schedule and actual credible capacity in a week

图11 中红色区域的上边界为风电的出力，下边界为调度计划传统考虑的风电容量，黑色虚线为风电运行可信容量，当黑色虚线落在红色区域内部时代表计算所得运行可信容量大于传统调度考虑容量。黑色虚线在较多时刻处于红色区域内部，较少时刻处于红色区域外部，实际上，在168 个小时中，共有101 个时刻的结果落在红色区域内部，这表明该星期的大量时刻下实际的风电运行可信容量要大于调度计划考虑的容量，传统基于风电预测功率的出力安排低估了风电的可信度，风电的实际容量可信度要大于对其的保守估计，具有更大的带负荷能力。由于本文对风电运行容量可信度的研究考虑了系统的运行可靠性水平不变，因此在传统调度计划中考虑风电运行容量可信度不仅不影响系统可靠性，还在部分时刻起到很好的辅助支撑作用，一方面能够减少常规机组出力或开机台数，减少成本，另一方面，对促进大规模风电消纳也具有重要意义。

5 结论

计算结果表明，风电各时刻的可信容量和容量可信度变化趋势并无跟随关系，在负荷水平相近的条件下，风电运行可信容量与出力大小基本呈正相关，而运行容量可信度的趋势虽然大体上与风电的出力趋势一致，但对于本文风电渗透率不高的情况，负荷水平与风电出力之间的相关关系也是影响各时刻风电运行容量可信度的重要因素之一。

同时，以一周为研究周期，对比了风电实际运行可信容量，与现有调度计划中考虑的风电容量之间的差异，结果表明传统安排一定程度上保守估计了运行层面风电的容量可信度，未能充分挖掘风电的带负荷能力。风电的运行容量可信度可以对传统调度计划起到辅助支撑的作用，减少了风能资源的浪费，促进风电的消纳率，对未来高比例新能源电力系统的调度运行有一定的参考意义。