中国全要素生产率的测算及分析

杨认真，魏 峰

(安徽大学 经济学院，安徽 合肥 230026)

一、引言

全球致力于追求发展的背景下，经济增长作为发展的重要基础备受瞩目。如何实现经济增长呢？索洛在新古典增长理论中对这一问题作出了回答。他指出，经济增长的方式有两种，增加要素投入数量和提高要素投入效率。但根据边际报酬递减规律可知，通过增加要素投入驱动经济增长的方式不具有持久性，要推动经济持续增长必须依靠提高生产率。相比单要素生产率，全要素生产率考察的范围更加全面和合理。因此，测算中国全要素生产率，并分析全要素生产率对经济增长的贡献率，对于中国经济发展和政府科学决策具有重要的意义。

刘云霞等对中国1953—2019 年的全要素生产率进行了测算，结果显示1953-1978年全要素生产率近乎为零，对经济增长的贡献也微乎其微；而1978年以后全要素生产率的值有了明显的提升，在经济增长中所占份额最高达到39.23%，由此认为改革开放以来，中国的经济发展并非只得益于增加要素投入，全要素生产率的提高对经济发展起到了至关重要的作用[1](P78-88)，得出类似结论的有蔡跃洲等[2](P72-88)、李平等[3](P84-111)、盛来运等[4](P3-11)。但周永锋研究发现1991—2015年全要素生产率的平均增长率为-0.32%，中国的经济增长主要来源于资本投入[5](P18-22)。

总得来看，国内学者在研究中国全要素生产率时所用方法和测算时期各不相同，结论也并不一致。目前，测算全要素生产率的方法主要有两大类：增长核算法和经济计量法。经济计量法要求可用的数据达到一定数目，中国现有的数据量相对较少无法满足其要求。增长核算法中的索洛余值法对数据的要求较低，且模型简单，易于理解，故成为现阶段国内学者使用最广泛的测算全要素生产率的方法。另外，自改革开放以来，中国经济社会在经济体制改革的影响下，发生了翻天覆地的变化，反映经济社会发展趋势的各类指标值也呈现出较大幅度的波动。基于此，本文采用索洛余值法对中国改革开放以来的全要素生产率开展测算研究，并同已有的测算结果做比较，以探求中国经济增长的真正动因。

二、全要素生产率的估算

(一)模型设定

索洛余值法的一般思路是先估算出总量生产函数，然后利用产出增长率减去劳动增长率和资本投入增长率后的残差来度量全要素增长率，所以也称索洛残差法。在规模报酬不变和希克斯中性技术的假设条件下，全要素生产率增长率等于技术进步率。

设总量生产函数为：

(1)式中Yt表示t年的总产出，Kt表示t年的资本投入，Lt表示t年的劳动投入，At表示t年除资本投入和劳动投入以外的所有要素的投入，主要表现为技术进步的影响，α、β分别表示资本投入和劳动投入的产出弹性。对(1)式两边取对数，并求全微分，可以得到：

InYt=InAt+αInKt+βLnLt

(2)

(3)

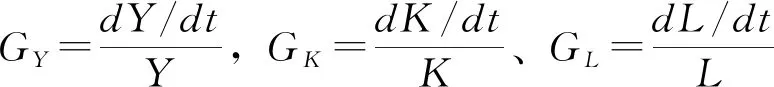
GA=GY-αGK-(1-α)GL(4)

设y、k和l分别表示总产出、资本投入和劳动投入平均增长率，则资本投入、劳动投入和全要素生产率增长率对总产出的平均贡献率EK、EL、EA可表示为：

(5)

(6)

EA=1-EK-EL

(7)

(二)指标口径和资料来源

1.总产出

衡量国民经济总产出的指标主要有国内生产总值(GDP)和国民生产总值(GNP)，从字面含义可以看出，它们之间并不完全相同。一般来说，GNP是在GDP的数据基础上，做适当调整得到的。与GNP相比，GDP涵盖的统计范围更广，也更能够准确地反映出一个国家的产出水平，故本文采用GDP来衡量总产出，数据来自《中国统计年鉴》。

2.劳动投入

一般认为，劳动投入情况不仅取决于劳动投入数量，与劳动投入质量及效率等因素也有很大的关系。《资本测算手册》中指出，劳动工时能够对劳动投入进行质量和效率上的调整，是核算劳动投入最为合适的指标。发达国家多采用劳动工时来核算劳动投入，而由于中国缺乏劳动工时的相关数据资料，国内学者通常采用历年的就业人数来核算劳动投入。考虑到数据的可得性，本文也选取历年的就业人数作为劳动投入的度量指标，数据来自《中国统计年鉴》。

3.资本投入

经济合作与发展组织(OECD)成员国家将永续盘存法作为估算资本存量的基本方法，其公式为：

其中，Kt表示t年的资本存量，It表示t年以当期价格计价的投资额，P表示t年的价格指数，δ表示折旧率。由上式可以看出，要得到资本存量序列，首先需要确定基期资本存量K0、历年投资额、价格指数和折旧率的值。

关于基期资本存量的估算有很多相关文献，基期不同，得到的估算结果也就不同；同一基期，若采用的估算方法不一样，得到的结果也不尽相同。其中以1978年为基期的估算结果有：华冬芳和李智勇参照张军和章元对资本存量的估算结果，结合固定资产价格指数，计算得到1978年的资本存量为8663.6亿元[6](P4-5)；李治国和唐国兴直接借鉴Chow的推算结果，将1978年的初始资本存量设定为14112亿元[7](P34-42,92)；黄勇峰和任若恩首先估算出中国早期的投资流，然后采用永续盘存法推算出1978年的初始资本存量为5821.66亿元[8](P378-396)。学者们普遍认为，K0值只对最初几年内的资本存量产生影响，在逐渐折旧的过程中，估算后期的资本存量的精准性将会逐渐提升。相对而言，黄勇峰和任若恩的估算结果更为准确，因此本文将1978年的初始资本存量确定为5821.66亿元。

目前，学术界并未对用什么指标来衡量投资流量做出明确的规定。以往文献中出现较多的指标主要有全社会固定资产投资总额和固定资本形成总额，两者均是国际上认可的用来反映全社会投资需求的指标，它们之间的区别主要体现在反映的角度上，前者从货币角度出发，而后者则是从最终使用角度出发。它是不包含存货的投资流量，更能真实地反映出实际的资本投入效果，因此本文采用固定资本形成总额作为投资流量的度量指标。

在周永峰的研究中采用固定资产投资价格指数对投资流量进行平减处理，但是从《中国统计年鉴》中只能获取1991年以后的价格指数数据，1990之前的数据无从查询。由此出现了两种较为流行的做法：一种做法是采用其他价格指标替代，如张军和章元在研究的过程中，采用上海市的固定资产投资价格指数来代替全国固定资产投资价格指数[9](P35-43,90)；另一种做法是采用自己的方法测算或合成，如李治国和唐国兴首先根据上海市的固定资本形成总额及其指数计算出上海市的固定资产投资价格指数，然后对1991-2000年的全国固定资产投资价格指数和上海市固定资产投资价格指数进行回归分析，拟合得到1978-1991年的全国固定资产投资价格指数序列，再与《中国统计年鉴》所公布的1991-2000年的数据结合，以此构建出完整的中国固定资产投资价格指数序列[7](P32-42,92)。

除此之外，还有部分学者通过固定资本形成总额和固定资本形成总额指数构造投资隐含平减价格指数来平减投资流量。如何枫等首先根据1952-1995年的固定资本形成总额和固定资本形成总额指数计算出1952-1995年的隐含投资价格指数，再根据固定资本形成总额平减指数和商品零售价格指数在1952-1995年间的回归关系估算1996-2001年的投资价格指数[10](P29-35)。与何枫等不同的是，赵志耘和杨朝峰通过拟合固定资本形成总额平减指数与GDP平减指数在1978-2004年间的关系来估算2005—2020年的投资价格指数[11](P3-12)。

鉴于已经选定固定资本形成总额来衡量投资流量，本文认为采用固定资本形成总额指数来平减历年的投资流量最合理。但《中国国内生产总值核算历史资料(1952—2004)》只公布了截止于2004年的固定资本形成总额指数，利用现有的数据无法完成换算。经过分析，本文决定借鉴赵志耘和杨朝峰的做法来构造投资隐含平减价格指数，具体构造关系如下：

IDt=0.962516GDPDt+8.995794

(9)

(9)式中IDt表示t年的固定资本所形成的总额平减指数，GDPDt表示t年的GDP平减指数，模型中涉及到27个观测值，R2=0.9896。

《中国统计年鉴》中指出，目前中国尚不具备对全社会固定资产进行重估价的条件，只能按照规定的固定资产折旧率的方法来提取固定资产折旧。因此，本文不对折旧率做过多探讨，将5%设定为资本折旧率。确定了以上所需数据，中国从1978年到2020年的资本存量可以用公式(3)估算。

4.劳动和资本产出弹性

估算产出弹性的方法主要有三种：份额法、回归法和经验法。在全要素生产率的研究中，牛龙[12]、杨营营采用了份额法[13]，周永峰采用了回归法[5](P18-22)，傅晓霞和吴利学同时采用了这两种方法[14](P12-22,95)，李静等[15](P12-22)、郑京海和胡鞍钢则是通过经验法设定出各要素的产出弹性[16](P777-808)。高宇明和齐中英指出用参数回归的方法估计各要素的产出弹性，在代入增量数据后，不一定满足方程的残差平方和最小的条件，因此可能会降低估算结果的准确性[17](P100-109,121)。经验法指研究者凭过往经验确定各要素产出弹性的值，最大的不足是主观性和随意性较大。份额法不受统计口径和样本序列的影响，同时可以有效地避开以上两种方法的许多问题，因此，本文采用份额法对劳动和资本的产出弹性进行估计。

已知两个产出弹性相加等于1，因此只要估算出劳动产出弹性，便可以很容易推算出资本产出弹性的值。假定劳动的贡献份额为1-α，则根据份额法劳动产出弹性1-α可以用以下公式来表示：

从《中国统计年鉴》中的国民经济核算的子栏目下，可获取31个地区按收入法核算的国民生产总值和劳动者报酬，把31个地区的相应数据进行加总，得到全国范围内的两项指标的数值。将所得数据代入(10)式，可计算出历年的劳动产出弹性。鉴于2008年《中国统计年鉴》中没有采用收入法核算国内生产总值，本文通过插值法取相邻年份的产出弹性进行代替。最终计算出2008-2017年劳动产出弹性的平均值为0.47，这与牛龙采用份额法计算出来的劳动产出弹性0.45相差不大，且与杨营营采用份额法计算出来的劳动产出弹性相同，故本文拟定资本产出弹性为0.47。

(三)全要素生产率的估算结果

根据上文所获得的数据，可以计算出总产出、劳动投入和资本投入的增长率。结合资本和劳动产出弹性的值，运用公式(4)，可得到历年的全要素生产率增长率。1978-2020年总产出的平均增长率为9.23%，劳动投入的平均增长率为1.53%，资本投入的平均增长率为11.44%，全要素生产率的平均增长率为2.44%。结合的值，可以进一步计算出资本投入、劳动投入和全要素生产率对经济增长的平均贡献率分别为65.73%、7.81%和26.25%，这表明改革开放以来中国经济的增长是由资本投入和技术进步的增长共同拉动的。为进一步验证测算结果的可靠性，本文收集了部分学者同期研究起点对中国全要素生产率增长率的测算结果，并将它们绘制在同一张散点图上，以此来做一下对比分析，如图1所示。需要注意的是，由于以上学者研究的时间区间存在差异，所以部分年份的数值无法获取。

图1 中国全要素生产率增长率的变化趋势图

由图1可以直观地看出，本文测算出来的全要素生产率增长率与赵志耘和杨朝峰、牛龙以及马丹丹测算出来的全要素生产率增长率变动趋势大体一致。具体表现为涨跌交替的阶段性状态，且近些年来波动趋势趋于平缓，这有力地支撑了本文的测算结果。其中，1990年全要素生产率增长率最低，这一点几乎在所有文献中都可以被证实。其原因是多元化的，例如20世纪80年代 末与90年代初通货膨胀问题日益严重，政府为缓解这种情况，制定了紧缩的经济政策。另外，东欧剧变以及苏联解体导致当时整个世界政治与经济动荡不安，对中国的出口贸易产生巨大的冲击也是其中一个重要原因。

三、结语

本文采用索洛余值法对中国1978-2020年的全要素生产率进行了估算，结果显示改革开放后，资本投入仍然是中国经济增长最主要的推动力，其贡献占到整个经济增长的65.73%。波动较为明显，是引起经济周期波动的主要原因；全要素生产率是中国经济增长的重要动力，其对中国经济增长的平均贡献率为26.25%，改革开放以来波动趋势趋于平稳，但增长率相对而言较低、劳动投入对经济增长的贡献率最低，其对于经济周期波动的影响也最小。另外，受到人口红利消失的影响，近些年来劳动投入对经济增长的贡献率正在缓慢下降。因此，应认识到全要素生产率对经济增长的重要性，通过增强自主创新能力和深化经济体制改革，进一步提高生产率水平。同时，深入实施人才强国战略，从实际出发解决人才队伍建设过程中存在的问题，并在全社会弘扬尊重劳动、尊重知识、尊重人才、尊重创造的良好社会风气，全面提高中国的人力资本水平，从而推动中国经济持续增长。