考虑粘结应力传递的抗弯加固锈蚀RC梁挠度计算方法

唐皇，彭建新，王晗，张建仁

(1. 湖南城市学院 土木工程学院，湖南 益阳 413000；2. 长沙理工大学 土木工程学院，长沙 410114；3. 国家电网益阳供电公司，湖南 益阳 413000)

钢筋锈蚀引起的钢筋与混凝土粘结力退化是导致钢筋混凝土(RC)结构承载性能降低的主要因素之一。利用钢板和FRP加固锈蚀RC结构是两种运用广泛且有效的加固方法。由于钢板具有加固操作方便、成本低、对结构本身破坏小等优点，已广泛运用于加固工程中。学者们对于未锈蚀加固结构承载性能和变形性能等方面的研究取得了诸多成果[1-3]，但对于钢板加固锈蚀RC梁力学性能的研究较少。近年来，笔者通过对30片不同锈蚀程度的RC梁进行不同方式的钢板加固，通过试验研究得到了钢板抗弯加固锈蚀RC梁抗力退化、变形性能和破坏特征[4-5]，分析了二次锈蚀对于钢板加固锈蚀RC梁后的承载性能的后续影响[6]，建立了计算钢板加固锈蚀RC梁的短期挠度计算方法[7]，此方法并没有考虑不同锈蚀状态下粘结应力的有效传递，而把粘结力作为定值，最终极限荷载对应的挠度值比较合理，但不同荷载等级下的挠度值与试验值略有差异。

FRP作为比较新型的加固材料，由于其刚度高、纵向拉伸强度大、抗腐蚀性好、热传递率低等优点，已经广泛运用于钢筋混凝土结构的加固工程中。粘贴FRP布加固RC结构是使用FRP材料增强RC结构性能的方法之一。学者们对FRP布加固锈蚀后的RC结构力学性能进行了一系列研究。Al-Saidy等[8-9]通过试验研究了不同锈蚀率下粘贴CFRP布加固RC梁的短期挠度、破坏模式和承载力等力学性能。Triantafyllou等[10]通过实验对比分析了轻度锈蚀、中度锈蚀和严重锈蚀对于粘贴CFRP加固RC梁的挠度、FRP应变和承载力等性能指标的影响。王晓刚等[11]研究了弱界面对CFRP剥离的影响及传统U型箍约束的有效性。以上学者主要是通过试验研究FRP加固锈蚀RC梁的力学性能，没有具体分析从理论上计算不同粘贴方式下FRP加固锈蚀RC梁的变形和承载力的方法。

笔者结合现有钢板和FRP加固锈蚀RC梁的试验和理论成果，考虑不同锈蚀情况下锈蚀钢筋和混凝土粘结-滑移导致的粘结应力传递以及传递前后梁截面应变相容性，利用微元法思想，建立不同破坏模式下钢板和FRP抗弯加固锈蚀RC梁的理论分析模型，并利用笔者和其他学者的试验研究结果验证理论模型的正确性。

1 抗弯加固锈蚀RC梁变形计算模型

1.1 锈蚀钢筋与混凝土粘结-滑移模型

学者们对于未锈蚀钢筋与混凝土的粘结性能的研究已经较为成熟[12-13]。对于变形钢筋，采用Haskett等[12]提出的经典粘结-滑移模型，如图1所示。当滑移很小时，粘结力随着滑移增加而增加。粘结力起初是因为混凝土与钢筋之间的化学粘附形成的，当混凝土内部微裂缝出现时，化学粘附消失，随着滑移继续增加，此时粘结力主要由混凝土与钢筋之间的机械联锁产生。当滑移持续增大导致混凝土开始剪切破坏时，粘结力最大，之后粘结力迅速减小，直至混凝土剪切脱落，此时粘结力称为残余粘结力，并保持不变，由混凝土与混凝土摩擦产生。图1中，从滑移开始到混凝土剪切脱落前的粘结力称为有效粘结力。

图1 经典粘结-滑移模型

采用双均匀模型来描述未锈蚀钢筋的粘结应力，这样可以简化计算，如图2所示。基于能量消散的等效性，图2中将粘结力分布简化为平均有效粘结力(矩形面积)和残余粘结力。无锈蚀钢筋与混凝土的平均有效粘结应力τub由Cairns等[14]提出的模型计算，见式(1)。

图2 有效粘结应力

(1)

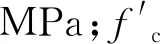
目前，对于锈蚀钢筋粘结性能的研究已经较成熟。有学者认为钢筋锈蚀将影响钢筋与混凝土之间的粘结力，锈蚀将导致钢筋与混凝土之间的粘结力退化[15-17]。采用Bhargava等[15]提出的较为简洁的经验模型来描述锈蚀钢筋粘结力与不锈蚀钢筋之间的关系。Bhargava等[15]通过大量的锈蚀构件拉拔试验和锈蚀梁弯曲加载试验，提出了锈蚀钢筋与不锈蚀钢筋平均粘结力之间的关系式

τcb=R(η)τub

(2)

式中：R为粘结强度系数；η为钢筋的锈蚀损失，%。

对于FRP抗弯加固的锈蚀RC梁，已有学者通过实验研究证明FRP材料有一定的阻锈作用[18]，同时，粘贴FRP布加固能提高锈蚀钢筋与混凝土的粘结强度。总结Soudki等[19]、Zhou等[20]、Papakonstantinou等[21]和Wang等[22]针对FRP材料加固锈蚀RC构件拉拔试验结果，对比同一锈蚀率下构件加固前后的最大粘结应力或者拉拔力，见表1，统计获得了加固后较加固前粘结应力增长率(图3中的红框点)，并且将增长率取均值(图3中黑色点)，获得了钢筋锈蚀率η和加固后粘结应力平均增长率K之间的关系曲线，发现两者服从极值分布关系，如图3所示。对于FRP加固锈蚀RC构件，钢筋平均粘结应力在同一锈蚀率下有所增加，见式(3)。

表1 FRP加固构件拉拔试验结果

图3 锈蚀率和粘结应力平均增长率的关系

K=58+119exp(-exp(-z)-z+1)

z=(η-25)/13.1

τcb=KR(η)τcb

(3)

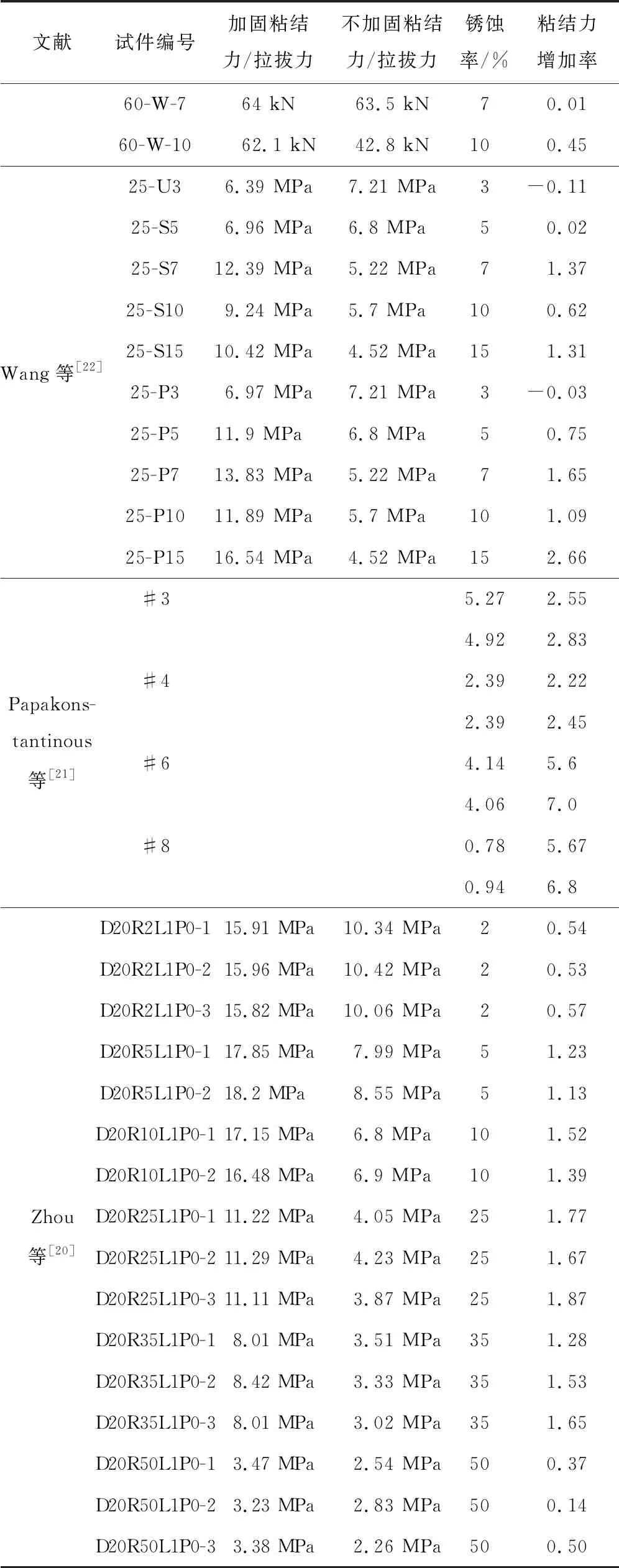
续表1

残余粘结应力τcbr比有效粘结应力小，根据CEB-FIP 规范[23]，残余粘结强度为平均有效粘结强度的40%。

根据ACI规范[24]，RC梁中变形钢筋的粘结锚固长度为

(4)

式中：ld为有效粘结区长度，mm；fsy为钢筋的屈服强度,MPa。

结合式(3)和式(4)可以获得锈蚀梁的有效粘结力Fcb为

Fcb=π×D×ld×τcbr

(5)

1.2 锈蚀RC梁加固后有效粘结力传递理论

从图4(a)中可以分析得出，钢筋的拉力Fs小于等于有效粘结力Fcb时滑移量很小，可以忽略。当钢筋的拉力超过有效粘结力Fcb时，有效粘结区将向梁端转移，如图4(b)所示，此时，拉力由有效和残余粘结力抵抗，直到两者的和等于拉力时，力传递结束。

图4 有效粘结力传递

对于不锈蚀梁和轻微锈蚀的RC梁，钢筋的拉力小于有效粘结力，没有明显的滑移出现，如图5(a)所示。RC梁的承载力和变形计算可以由传统应变相容的方法进行。

当钢筋的锈蚀程度不严重时，粘结力出现退化。RC梁加载过程中，钢筋的拉力大于有效粘结力，此时，有效粘结力将传递到梁末端来抵消钢筋拉力，当拉应力等于有效粘结力时，传递停止，如图5(b)所示。同时，钢筋与混凝土应变存在不相容的现象，在计算承载力和变形时要考虑应变不相容。

当钢筋出现严重锈蚀时，有效粘结力很小，并且有效粘结区域很快向梁端传递，如图5(c)所示。当梁端锚固较好时，梁还可以继续承载，此种情况类似于无粘结后张预应力梁。

图5 粘结滑移模型

通过以上分析可以获得不同锈蚀情况下的锈蚀RC加固梁从加载到破坏过程中的应变和受力分析，进而获得加载过程中的荷载-挠度曲线。

1.2.1 有效粘结力传递前的应变相容分析 对于不锈蚀和轻微锈蚀梁抗弯加固后，梁各个部分的应变是相容的。应变分析图见图6。对于任意截面i，纵向受拉钢筋、受压钢筋和加固钢板或FRP材料的应变可表示为

图6 加固梁应变分布

(6)

式中：εsi和ε′si分别为受拉和受压钢筋应变；h为梁高,mm；εcti和εcbi分别为梁顶面和底面的混凝土应变；h0和a′s分别为受拉和受压钢筋到梁顶面的距离,mm；εpfi为加固材料应变；t为加固材料厚度,mm。

锈蚀钢筋的应力-应变关系采用张伟平等[25]提出的模型，见式(7)。根据此模型和钢筋锈蚀率可以获得任意截面i纵向钢筋和受压钢筋拉力，见式(8)。

(7)

Fsi=(1-η)Asfsi

(8)

式中：εshc和εsuc分别为屈服后的强化应变、极限应变；Es0为未锈蚀钢筋的弹性模量，MPa；fyc为锈蚀钢筋屈服时的钢筋应力，MPa；fuc为锈蚀钢筋极限应力，MPa；As为不锈蚀钢筋横截面积,mm2。

图7为采用的混凝土受压应力-应变关系[26]。图中εc为受压区顶部混凝土应变；εc0为混凝土抗压强度对应的应变；εcu为混凝土极限应变。

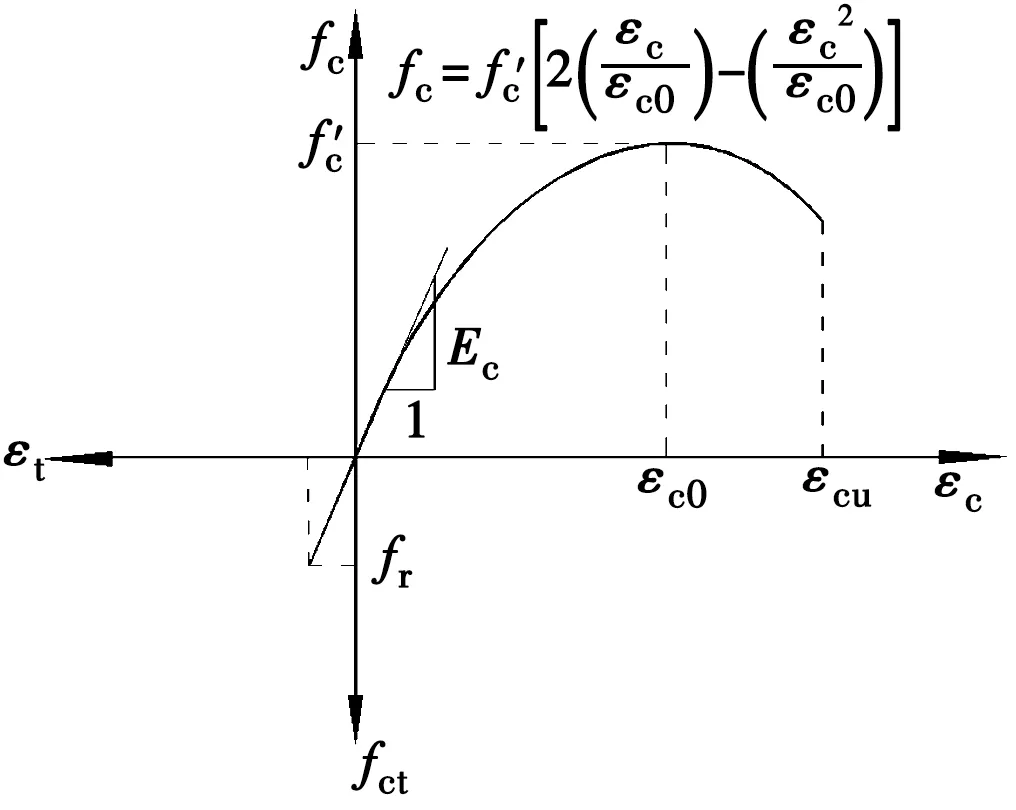
图7 混凝土本构关系

计算模型中忽略混凝土的抗拉强度。混凝土的压力Fci可以采用对梁从底面到顶面的有限积分的方式进行计算，见式(9)。

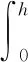
(9)

式中：y为梁顶面至截面任意位置的高度,mm。

加固材料的拉力Fpfi可以由式(10)计算。

Fpfi=εpfiEpfApf

(10)

式中：Epf为加固材料弹性模量,MPa;Apf为加固材料横截面积，mm2。

从梁顶面至混凝土等效合力点的位置高度ybi为

(11)

根据力学平衡，可以获得受拉和受压纵向钢筋、混凝土以及加固材料之间的平衡关系为

Fci+F′si=Fsi+Fpfi

Fci(h0-ybi)+F′si(h0-a′s)+0.5Fpfi(t+as)=Mi

(12)

式中：as为梁底部中部至受拉钢筋截面中部的距离,mm；F′si为受压区钢筋压力,N。

1.2.2 有效粘结力传递发生后的应变不相容分析 当有效粘结力传递发生后，钢筋、混凝土和加固材料的应变便不服从平截面假定，但在滑移区纵向钢筋与混凝土的滑移总量相等。基于此原则，便可分析三者之间总的应变关系以及有效滑移区长度。将加固梁可能存在的最大滑移区划分为1到g段，如图8。滑移区长度假设为Ls，滑移区内的梁节段从m到n。纯弯段长度从e到f。对于给定的荷载P，假设出现了滑移，在滑移区两个末端，钢筋拉力(Fsm和Fsn)应该与有效粘结应力相等，根据此原理可以求得滑移区内部任意截面钢筋的拉力，见式(13)。

图8 梁段单元划分

(13)

钢筋的应变可以由式(14)获得。

(14)

进而可以获得受拉钢筋的纵向总延伸为滑移区内部各节段延伸与两个锚固区内的延伸总和，见式(15)。

(15)

式中：ΔLs为滑移区内纵向钢筋延伸率；li为节段长度,mm；ss为有效粘贴区内纵向钢筋的滑移值,mm，如图1，这个滑移值很小，为简化计算可忽略。

每节段钢筋的拉力Fsi已知，通过式(12)可以获得混凝土顶部应变εcti、底部应变εcbi和加固材料的应变εpfi，钢筋周围混凝土应变εcsi为

(16)

滑移区内混凝土的总的延伸长度为

(17)

式中：ΔLc为混凝土在滑移区的延伸值,mm。

1.3 计算加固梁荷载-挠度曲线

基于应变分析，通过编制循环程序获得每一级荷载作用下加固梁段钢筋、混凝土和加固材料的应变，进而获得梁的挠度。程序的具体可以分为4个阶段：

阶段1：计算有效粘结力Fcb、梁端锚固长度ld，滑移区长度最大值Lmax。

阶段2：有效粘结区域传递前。1)设定较小荷载值P，计算每个梁段的弯矩Mi；2)计算钢筋的拉力Fsi，当Fsi大于有效粘结力Fcb时，转到第3阶段。

阶段3：有效粘结区域传递中。1)假设滑移区长度Ls；2)计算滑移区内节段受拉钢筋拉力Fsi，受拉钢筋和混凝土延伸长度ΔLs和ΔLc；3)修改Ls直到受拉钢筋与混凝土的总延伸长度相等，输出Ls。

阶段4：粘结滑移区域传递完成后。1)Ls已知，其值为最大有效粘结长度Lmax；2)Fsn和Fsm未知，重新设定两者数值，再进行循环计算；3)以ΔLs=ΔLc为判据停止循环，同时，根据加固梁破坏模式确定破坏荷载，并给出挠度曲线。

模型中挠度曲线可以由式(18)、式(19)获得。

(18)

espi=εspili

(19)

式中：xi为梁支座顶点到i单元的距离,mm；N为单元总数；hsp为加固后梁截面的换算有效高度,mm，即锈蚀后的受拉钢筋和加固材料合力作用点到梁顶的距离；εspi为每一单元中hsp所对应的截面有效平均应变，即加固材料和钢筋的组合应变。

程序中考虑了钢板和FRP抗弯加固锈蚀RC梁的破坏模式。张建仁等[4]通过试验研究发现抗弯加固锈蚀率为5%、10%和15%的RC梁破坏模式为斜截面斜拉破坏，钢板端部混凝土拉裂。文献[9-10]中试验研究发现，FRP加固锈蚀RC梁的破坏模式通常为钢筋抗弯屈服以后FRP材料在梁中部断裂或者FRP脱落，因此，当获取FRP加固梁的极限荷载时，前者钢筋应变达到屈服应变并且FRP应变达到极限应变，受压区混凝土压碎，后者受拉钢筋屈服，FRP不一定达到极限强度，受压区混凝土压碎。

根据以上步骤，具体的程序框图见图9。

图9 模型程序流程图

2 模型验证

为了验证提出的理论模型的正确性，选取了唐皇[27]、Al-Saidy等[8]、Triantafyllou等[10]、邓文明[28]进行的锈蚀RC梁钢板和FRP抗弯加固试验数据，利用其短期荷载-挠度曲线与理论计算结果进行对比，并对比了理论模型和张建仁等[7]提出的模型的精确性。图10为唐皇[27]进行的钢板抗弯加固锈蚀RC梁试验与理论分析的对比结果，图11为其他学者进行的FRP材料加固锈蚀RC梁试验与理论分析的对比结果。表2为理论值与试验值极限荷载和对应的挠度对比，表2中1为模型理论值与试验值的误差，2为张建仁模型理论值与试验值的误差。

图10 钢板抗弯加固不锈蚀和锈蚀RC梁荷载-挠度曲线

图11 FRP抗弯加固锈蚀RC梁荷载-挠度曲线

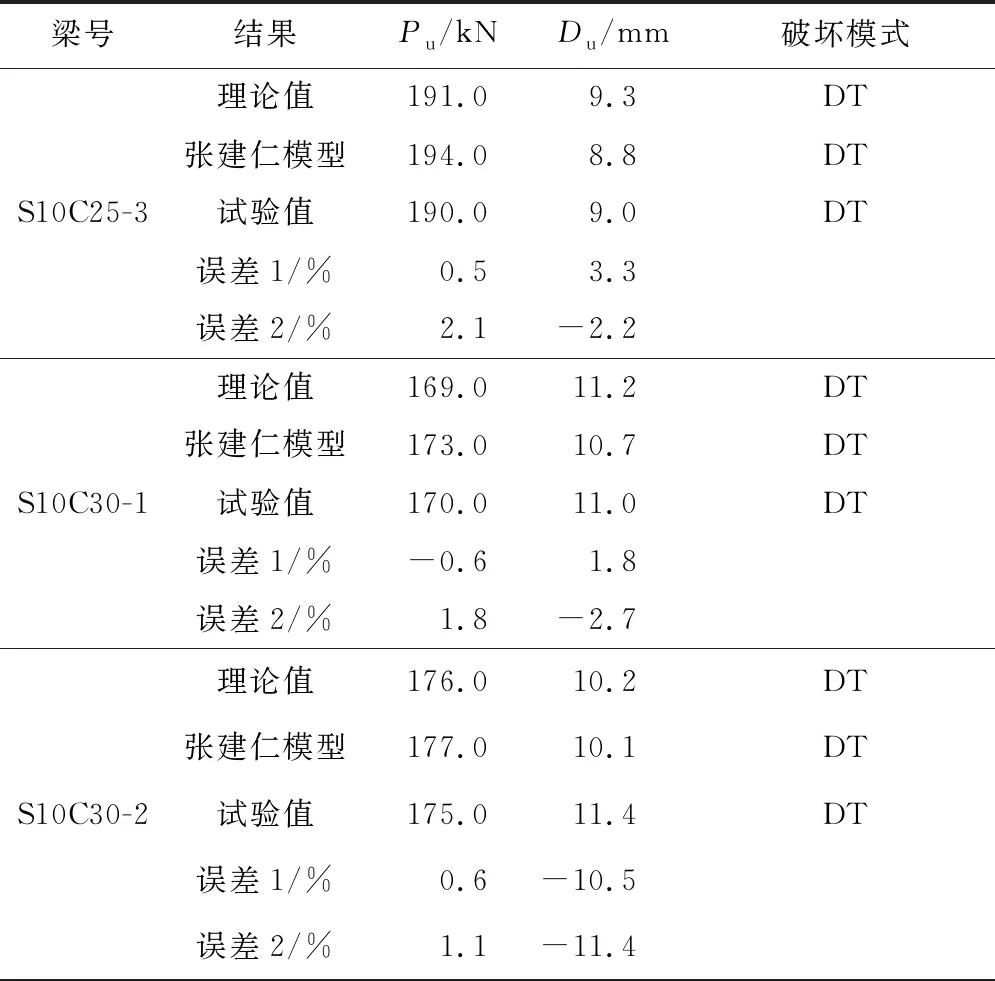
表2 锈蚀加固梁试验值与理论值对比

续表2

续表2

续表2

从表2可以看出，绝大多数试验梁理论破坏模式与试验破坏模式相同，钢板加固不锈蚀梁S0C25-1的破坏模式却有差异，其极限挠度试验值与理论值较其他试验梁差别大，是由于试验梁的制作加工问题，试验出现了提前斜拉破坏的情况，导致挠度偏低。

从图10中也可以看出，理论计算值比张建仁模型计算值整体上更加接近试验值。张建仁等在试验中发现，钢板抗弯加固梁破坏时，锚钉与混凝土以及钢板之间没有出现滑移，因此，试验加固锈蚀梁的破坏多为钢板和受拉钢筋之间的混凝土拉裂破坏，与本文的加固梁假设相似。同时，锚钉位于保护层内，对钢筋与混凝土之间的粘结影响较小。张建仁等[7]的计算结果中，在同一荷载作用下挠度值比试验值偏小，其原因可能是模型中虽然划分了若干单元，但纵向钢筋粘结力沿梁长每个单元为相同的定值，没有考虑粘结力的传递，因此，与该模型相比，缺少粘结应力传递后的应变不相容分析，所有微梁段的应变分布相同。对比极限承载力和对应的挠度大小，理论模型与试验值的误差分别是-0.6%～1.8%、-10.5%～9.1%，张建仁模型理论值与试验值的误差分别是1.1%～6.1%、-11.4%～-2.2%。

从图11中可以看出，无论是CFRP(Al-Saidy等[8]、Triantafyllou等[10])和BFRP(邓文明[28])加固锈蚀RC梁，模型能较好地预测其荷载-挠度曲线。从表1中可以看出，极限荷载值的误差为-3.6%～4.2%，极限挠度误差为-4.2%～8.3%。

图10(a)和11(c)中还列出了钢板和BFRP加固不锈蚀梁的荷载-挠度曲线，其理论计算结果也可由该模型获得，程序只需计算阶段1和阶段2，结合式(18)和式(19)便可获得理论的荷载-挠度曲线。从图10(a)和图11(c)中可以看出，不锈蚀加固试件S0C25-3 和S1-0的理论荷载挠度-曲线与试验曲线都比较吻合。由表2中可以看出，钢板和BFRP加固不锈蚀RC梁极限荷载和对应的挠度误差分别是：2.8%、13.9%、1.6%、8.4%。

从Bhargava等[15]的粘结力模型中可以看出，当钢筋锈蚀率大于1.5%时，构件粘结力就开始退化，但Zhang等[29]指出，当钢筋的锈蚀率低于7%时，钢筋与混凝土应变不相容现象不明显，因此，对于锈蚀率低于7%时的试验梁将不考虑粘结力传递，循环计算只考虑阶段1和2。图10和图11所选取的试验梁中，梁M5S2锈蚀率为5%，其他梁均大于7%。从图11(b)中可以看出，梁M5S2的挠度在同一荷载下略大于理论值，这可能是因为其钢筋发生了轻微的粘结-滑移，粘结力传递发生了，但传递长度很小，导致同一荷载下的挠度稍微变大，但是增大的幅度很小，基本可以忽略不计。因此，从上述分析中可以看出，该理论模型也能较精确地预测不考虑粘结力传递的试验梁(不锈蚀梁和微锈蚀梁)荷载-挠度曲线。

3 结论

考虑不同锈蚀情况下锈蚀钢筋和混凝土的粘结-滑移导致的粘结应力滑移，利用微元法思想，建立不同破坏模式下钢板和FRP抗弯加固锈蚀RC梁的理论分析模型，并且利用现有试验结果对比分析了该模型的精确度，获得了以下结论：

1)计算模型考虑了不同锈蚀状态下粘结应力传递，同时进行了应力传递前后应变相容性和不相容性分析，与现有模型相比，能更准确地模拟了抗弯加固锈蚀RC梁荷载作用下的变形过程，同时也可以较精确地预测不锈蚀加固梁和微锈蚀加固梁的荷载-挠度曲线。

2)对于钢板抗弯加固锈蚀RC梁的挠度计算结果，在不同荷载等级下，考虑粘结应力传递模型的结果与不考虑粘结应力传递模型的计算结果相比，与试验值更接近。前者极限荷载和对应极限挠度的误差范围为-0.6%～1.8%和-10.5%～9.1%，后者极限荷载和对应极限挠度的误差范围为1.1%～6.1%和-11.4%～-2.2%。

3)考虑粘结应力传递的计算模型同样能较为精确地预测FRP抗弯加固锈蚀RC梁的荷载-挠度曲线，极限荷载值的误差范围为-3.6%～4.2%，极限挠度误差范围为-4.2%～8.3%。