桶形基础二次加载的大变形有限元模拟

陈霄，郑敬宾，王栋

(中国海洋大学 山东省海洋环境地质工程重点实验室，山东 青岛 266100)

近年来，负压桶形基础(以下简称为桶基)作为单桩基础和导管架桩基的替代形式，已用于支撑多个海上风电场的风机和升压站，如英国的Hornsea 3项目[1]。与风机的一次性吊装不同，桶基支撑的升压站平台分两个阶段安装：第1阶段，桶基与平台贯入土中预定深度，施工船返回港口，桶基静置数周至数月；第2阶段，各种大型电气模块运输至场地，并吊放到平台上，桶基实质上承受二次加载。第1阶段的桶基贯入在黏土中引起超静孔压，之后孔压部分或完全消散[2-3]，导致第2阶段开始时桶基周围黏土的不排水强度高于第1阶段结束时。

类似于一般的浅基础承载力问题，常规有限元方法被广泛用于分析不排水条件下桶基的竖向承载力及复合承载力[4-6]，但这些研究均假定桶基预埋就位，不考虑桶基安装过程对承载力的影响。这是因为桶基长距离贯入导致侧壁端部周围土体单元的严重扭曲，常规有限元方法无法捕捉这一大变形过程。

研究者借助离心机试验[7-11]或大变形有限元模拟[12-13]再现了桶基的贯入，探究了土层分布、安装方式、基础尺寸等一系列影响桶基贯入阻力的因素，提出了确定第1阶段贯入阻力的方法。少量的数值模拟还进一步给出了桶基安装后的孔压消散过程[3]，但这些结果仅评估了地基土的固结程度，不能预测升压站平台第2阶段的抗压承载力。Jeanjean[14]在墨西哥湾海域进行了现场试验，并总结了历史上该区域的施工记录，得到桶基安装就位时的贯入阻力以及固结一段时间后的抗拔力，发现桶基在安装后存在显著的固结效应，最终抗拔力最高可达初始贯入阻力的1.6倍，但其试验针对的是抗拔力，而不是抗压承载力。

鉴于与桶基二次加载有关的研究较为有限，笔者发展了有效应力形式的大变形有限元方法，模拟黏性土中桶基的“贯入-固结-二次加载”完整过程，探索桶基初始贯入和部分排水固结后的超静孔压分布，进而考察固结效应对二次加载的影响，合理评估二次加载的竖向承载力。

1 研究方法

1.1 大变形有限元方法

桶形基础的安装是典型的岩土工程大变形问题，因此使用一种名为RITSS的大变形有限元方法(Remeshing and interpolation technique by small strain)。这种方法最初由Hu等[15]提出。Wang等[16-17]将其与有限元商业软件Abaqus结合并扩展至有效应力分析。RITSS方法中，整个计算过程被划分为一系列小变形计算步，通过网格重划分及场变量映射，避免了单元的严重扭曲，具体细节可参见文献[17-18]。

采用基于Abaqus的RITSS方法，将桶基的“贯入-固结-二次加载”过程简化为二维轴对称问题进行分析，建立如图1所示的数值模型。桶基的长度、直径和厚度分别为L、D和t，支撑电气平台的桶基长径比L/D一般为1左右。为避免边界效应，土体的径向与竖向边界分别取5D与8D。约束底边径向边界的水平与竖向位移，竖向边界的水平位移。桶基周围附近土体的网格尺寸为1.5t。为提高计算效率，并避免贯入初期土体表面单元的剧烈变形，将桶基预埋一定深度。后文将证明该设置对后续贯入阻力的影响可以忽略。采用二阶轴对称缩减积分单元划分土体，以保证映射精度[17]。

图1 有限元模型范围与网格

采用罚函数法定义“桶-土”界面的摩擦力，在有效应力分析中，根据库伦摩擦定律，摩擦力取决于法向有效应力及界面的库伦摩擦系数。安装造成桶基周围土体的应变软化，设计时一般假定周围土体完全扰动。Koh等[3]采用大变形方法模拟桶基贯入时取摩擦系数为0.3tanφ′/St，其中φ′为有效内摩擦角，St为灵敏度，得到了与离心机试验结果相近的贯入阻力。笔者的数值分析也采用相同的摩擦系数。

以往离心机试验[7-11]比较了吸力式安装(即通过气泵从桶盖与土体之间抽水以施加吸力)与纯压入式安装(即采用位移控制使桶基贯入)两种桶基贯入过程，发现安装方式对黏土中桶基贯入阻力的影响可以忽略不计。因此，通过位移控制模式实现桶基的初始贯入和二次加载。在固结阶段，桶基上的竖向力保持为定值，竖向力大小等于当前深度的初始贯入阻力。在整个“贯入-固结-二次加载”过程，仅允许土体表面边界排水，其余各边均为不排水边界。

1.2 土体本构模型

采用经典的修正剑桥模型描述黏性土的有效应力与应变之间的关系，该模型已被成功用于分析静力触探仪、桩靴基础的大变形贯入[18-19]。考虑两种广泛用于离心机试验中的黏性土，即UWA高岭土和Malaysian高岭土，相关计算参数总结于表1。侧压力系数K0=1-sinφ′=0.61，浮重度γ′取6.76 kN/m3。

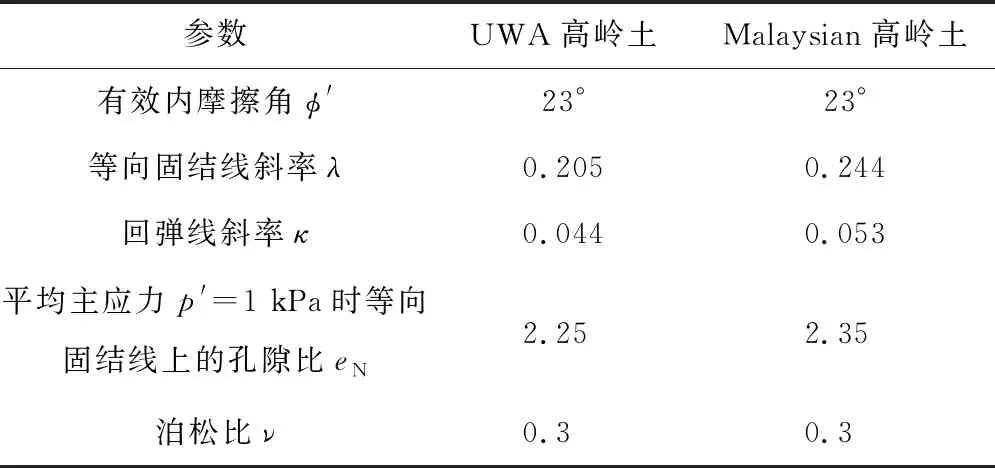
表1 土体参数[9,20-21]

根据临界状态土力学理论，轴对称条件下的不排水强度su为[22]

(1)

基于修正剑桥模型，K0状态下，正常固结土的孔隙比e与深度z的关系可以表示为

(2)

式中：C为等向固结线与K0固结线的竖向距离,m。根据临界状态理论与表1中的参数，UWA高岭土与Malaysian高岭土的C分别为0.048与0.057，而渗透系数k与孔隙比e的关系可表示为[18]

(3)

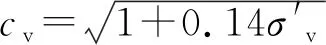
2 数值模拟验证

目前，还没有公开发表的桶形基础二次加载模型试验或现场监测数据。通过对比桶基首次安装时的贯入阻力，验证数值模拟的可靠性。Westgate等[9]完成了6个桶基在UWA高岭土中贯入的离心机试验。使用RITSS方法模拟其中名为Type1的试验。桶基的原型尺寸为D=11.3 m，L=6 m，t=0.05 m。试验前和试验后分别进行两次T-bar试验，得到土体的平均抗剪强度su=10+2.8zkPa。利用两次循环插拔T-bar试验获得土体的灵敏度St为2.5和3。大变形有限元分析中使用St=3，确定桶-土摩擦系数。试验中测得γ′=5.9 kN/m3，根据式(1)推导得到修正剑桥模型中的su=1.44zkPa。为便于比较，将贯入阻力F归一化为F/suA，A为桶形基础竖向投影面积，A=πD2/4。图2比较了离心模型试验[9]、有效应力形式的RITSS法、总应力形式的耦合欧拉-拉格朗日有限元法(Coupled Eulerian-Lagrangian，CEL)结果[13]、DNV规范的预测[23]。图中的纵坐标为归一化贯入深度d/D，即贯入深度与桶基直径之比。

DNV规范与CEL的结果均基于总应力分析，假定安装时地基土完全不排水。其中DNV规范建议周围土体的强度折减系数α=1/St=0.33，表示桶的最大侧壁摩阻力为αsu。文献[13]中CEL分析使用的系数为α=0.2，故图2也给出了α=0.2时的DNV方法预测结果。由图2可见，有效应力形式的RITSS方法和总应力形式的CEL方法给出的结果都与试验数据接近，且均在DNV公式预测的α=0.2和α=0.33两条曲线范围内。采用RITSS方法时，预埋使得计算曲线从0.2D开始，因此，无法比较0～0.2D范围内的结果。然而，当桶基的贯入深度超过0.25D后，贯入阻力曲线与试验非常接近，表明一旦土体破坏模式被完全激发，预埋对贯入阻力不会产生明显影响，这与已有结论一致[18-19]。图2的比较也表明大变形有限元分析中的摩擦系数取值合理，可以在很大程度上考虑安装扰动对贯入阻力的影响。

图2 数值模拟、离心机试验、规范预测结果的比较

3 结果分析与讨论

实际工程中钢制桶基的壁厚一般小于0.05 m。试算发现，当桶基侧壁厚度较小时，有效应力形式的大变形分析不易收敛，后续分析中统一取壁厚为0.19 m。Xiao等[13]比较了侧壁较厚(t=0.2～0.6 m)与较薄(t=0.05 m)的桶基端部承载力系数，发现其范围在10～12之间，表明一定范围内壁厚的增加没有改变桶基贯入时端部以下土体的破坏模式，而侧壁附近的土体破坏模式不依赖壁厚。因此，增加壁厚不会显著影响大变形结果。

表2总结了变参数分析中开展的算例。为探究固结系数cv的影响，算例A～算例D分别模拟了桶基在UWA高岭土和Malaysian高岭土中的“贯入-固结-二次加载”过程。这两种土的本构模型参数接近，但渗透系数相差很大，相同应力水平下Malaysian高岭土的cv约为UWA高岭土的10倍。算例A～算例D还将用于考察首次安装深度zp对二次加载的影响。算例E和算例F将考察桶基直径D对二次加载的影响。表2中的固结时间tc在7～360 d之间变化，其下限是实际工程中最短的施工间隔，而上限人为取得较大，以便展示充分固结造成的二次加载效应。

表2 变参数分析考虑的工况

修正剑桥模型并不能考虑土体结构性的影响，分析中摩擦系数始终保持为0.3tanφ′/St，这也意味着固结前后的土体灵敏度未改变，即不考虑扰动的土体结构在固结过程中部分恢复，所以，计算结果偏于安全。以下分析中统一取典型值St=2.5。

3.1 固结时间对二次加载的影响

算例A、C(D=9.5 m，首次贯入深度zp=0.9D)，固结7、30、60、120、270 d后，二次加载贯入阻力随深度的变化如图3所示。为了直观显示固结时间的影响，图中包含了初始连续贯入阻力曲线作为参考。参考Wang等[19]对桩靴基础贯入阻力的处理方法，利用峰值贯入阻力比Ncp/Ncr表征贯入阻力的改变，如图3(a)所示。Ncp为二次加载时归一化的峰值贯入阻力，Ncr为Ncp出现深度处归一化的初始贯入阻力。

图3 固结前和固结后的归一化贯入阻力(zp=0.9D)

从图3可以看出：

1)桶基的二次加载阻力在很短位移内即可达到峰值，Ncp出现时的深度仅略大于初始贯入结束时的深度zp。

2)UWA高岭土中即使固结时间仅有7 d，峰值贯入阻力也会增加约20%，见图3(a)。如果固结时间为7～120 d，二次加载的Ncp随固结时间增大，说明固结导致的桶基竖向承载力显著提高。但120 d后的Ncp基本不再增加。

3)二次加载的贯入阻力曲线达到峰值后迅速降低，并向初始连续贯入阻力曲线靠近。这表明，尽管施工间隔期间桶基周围土体固结，强度增加，但强度增加土体的范围有限。这一特征与桩靴基础的二次贯入类似[19]。

4)Malaysian高岭土的结果表现出与UWA高岭土类似的趋势，如图3(b)所示，Ncp/Ncr最大约为1.35。然而，固结60 d后Ncp就不再有显著增长。产生这种差异的原因是两种土的固结系数cv不同。Malaysian高岭土的固结系数远高于UWA高岭土，初始贯入造成的累积孔压在固结阶段消散得更快，桶基周围土体更快达到强度增长极限。

图4展示了固结过程中桶基附近3个位置的土体超静孔压消散过程。3个位置分别为桶壁端部中心、端部上方0.02zp处与桶壁紧邻的内侧与外侧。为避免固结初期孔压重分布对消散曲线的影响，利用Sully等[24]提出的方法确定每一个位置的名义初始孔压Δumax，得到归一化孔压Δu/Δumax随固结时间的变化曲线。图4表明，3个位置处的超静孔压消散规律几乎一致。对于UWA高岭土，孔压在最初的120 d迅速消散，120 d后的消散速度逐渐减缓，这与峰值贯入阻力的增长规律一致(图3)。同样，Malaysian高岭土中超静孔压在前60 d急剧下降，且消散速度比UWA高岭土更快。

图4 孔压消散曲线(zp=0.9D)

图5(a)为桶基在首次安装时的土体位移增量场，可见端部的土体主要流向桶内，这与Xiao等[13]的结论一致。固结后贯入至0.91D时(图5(b))，端部置换的土体也主要向桶内移动，且此时桶内土塞的高度略大于桶外。通过比较发现，固结并未改变端部土体的流动模式。

图5 算例A固结前后土体流动模式的比较

3.2 峰值贯入阻力比的变化规律

图6展示了峰值贯入阻力比随归一化固结时间T的变化。T按式(4)定义。

图6 峰值贯入阻力比与归一化时间的关系

(4)

式中：cv,z为深度zp处的固结系数。T实际上包含了多个因素的耦合影响：tc代表了固结时间；D代表了桶基几何形状；cv,z代表了土体的固结性质；初始贯入过程的影响则通过zp体现。

由图6可以看出，zp/D在0.7～1.5范围内时，两种高岭土参数计算得到的峰值贯入阻力比随归一化时间的变化趋势一致。曲线整体上可以分成两段：当T小于0.015时，Ncp/Ncr随T大致呈线性增长关系；当T大于等于0.015时，Ncp/Ncr趋近于一个稳定值。为了建立Ncp/Ncr与T的关系，在图6中添加了趋势线。地基土充分固结完成时，算例A的Ncp/Ncr达到1.36，算例F的Ncp/Ncr约为1.26，其他算例结果介于二者之间。也就是说，完全固结时二次加载得到的峰值贯入阻力最少增长约26%。

实际条件下，峰值贯入阻力的增长可能超出图6的有限元结果，这是因为在固结过程中孔压消散以及土体结构性的恢复都可以造成后续承载力的上升，且二者的贡献程度相当[14]。受限于本构模型，本文的有限元分析还不能反映土体结构性的恢复，所得峰值贯入阻力增长程度偏于保守。

4 结论

采用有效应力形式的大变形有限元方法模拟海上风电升压站平台的安装过程，再现了桶基“贯入-固结-二次加载”的全过程。数值模拟中考虑了两种力学性质接近，但固结系数相差10倍的高岭土，考察了固结时间、首次安装深度、桶基直径等关键变量对二次加载时贯入阻力的影响。主要结论如下：

1)当固结时间相同时，高固结系数土中二次加载的贯入阻力增长更迅速，但固结系数对峰值贯入阻力比极限值的影响不大，完全固结时的峰值贯入阻力比在1.26～1.36之间。

2)式(4)定义的归一化固结时间较好地反映了峰值贯入阻力比的变化趋势。采用归一化固结时间表征固结程度时，峰值贯入阻力比随归一化固结时间约为线性增加，直至达到极限值。

3)实际施工中，应充分利用二次加载前的施工间隔时间，发挥地基土固结后的强度，从而提高二次加载时的极限承载力，达到优化基础尺寸，降低工程造价的目的。