预应力部分外包钢组合梁变形性能试验研究

张鹏，赵晓冬，邓宇

(广西科技大学 土木建筑工程学院，广西 柳州 545006)

随着城市化与工业现代化建设的快速发展，城市人口大量增加，这给城市建筑物的空间需求带来巨大挑战[1]。因此，迫切需要具有自重轻、跨度大、截面尺寸小和节约材料等特性的新结构形式出现。预应力部分外包钢组合梁是一种将混凝土浇筑在H型钢腹板两侧，将H型钢上、下翼缘裸露在外并配置预应力筋的新型组合梁结构[2-4]。预应力部分外包钢组合梁的外包型钢可以对内部的混凝土起到包裹、约束作用，提高了构件的整体刚度并有效避免了钢构件的平面扭转屈曲性能，同时，结构的耐火性、耐久性与延性性能也充分提高[5-6]。此外，预应力技术的加入还可以较好地抑制混凝土的开裂[7]，因而在大跨度高层建筑及桥梁结构中有着广阔的应用前景。

学者们对部分外包钢组合梁的受力性能进行了大量试验，以探究其受力规律。Anwar Hossain等[8-9]对型钢腹板内填充混凝土的组合梁进行了大量试验研究，总结出混凝土与钢板截面黏结-滑移力学模型；Nakamura[10]对U型外包钢组合梁进行了承载力性能试验，分析其受弯承载力影响因素；李国强等[11]对型钢腹板嵌入式组合梁展开了抗弯性能试验研究；张道明[12]对预应力部分外包钢组合梁进行了抗弯性能分析；李业骏等[13]、丁保安等[14]对不同外包钢混凝土组合梁的延性性能展开了深入研究；杜德润等[15-16]对部分外包钢组合简支梁进行了抗剪性能分析与型钢抗滑移分析，此外，还对部分外包钢组合连续梁进行了内力分布分析。但学者们对预应力部分外包钢组合梁结构的变形性能尚未有针对性试验，在中国，还没有相关规范或规程对该结构的设计作具体规定。因此，笔者对12片预应力部分外包钢组合梁结构进行竖向两点加载试验，从裂缝开展、挠度与延性性能3个方面对该结构展开变形性能研究。采用分型维度理论[17]对各梁试件进行裂缝开展分析；利用Euler梁理论与Timoshenko梁理论推导梁的挠曲线方程与跨中挠度计算值；利用灰度关联分析法对预应力部分外包钢组合梁位移延性系数、截面曲率延性系数与能量延性系数展开影响因素分析。

1 试验概况

1.1 试件设计与制作

共设计制作12片预应力部分外包钢组合梁试件，各试件的基本参数如表1所示。

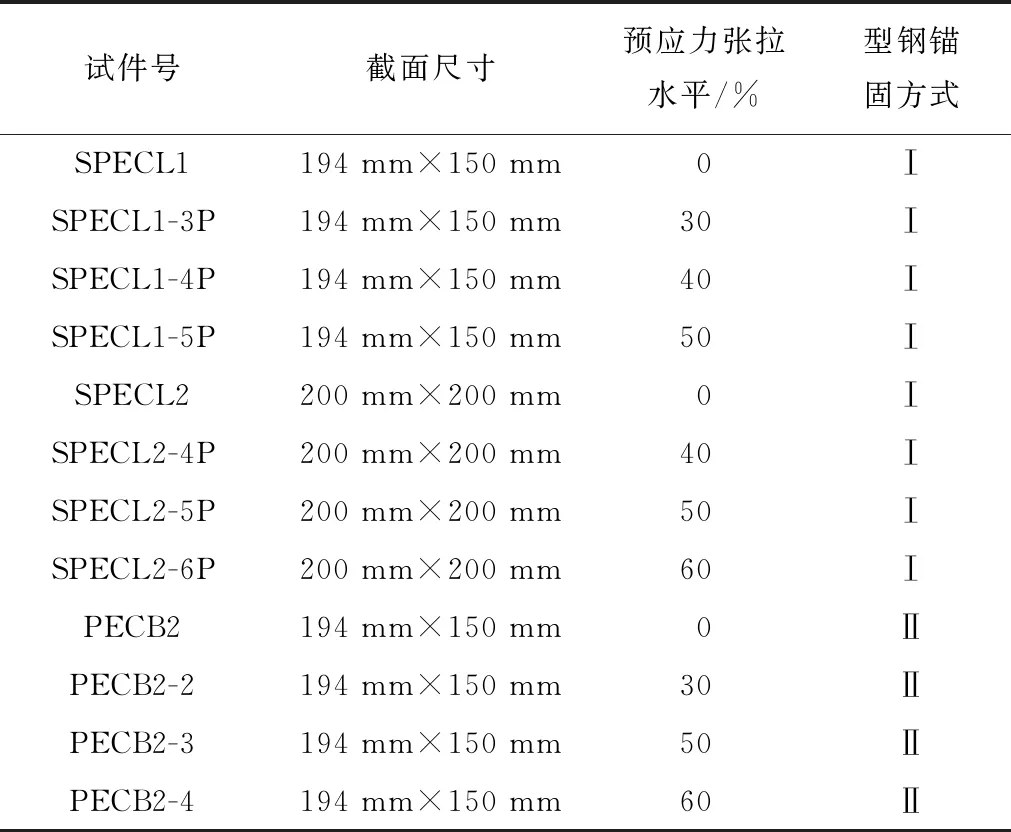
表1 各试件参数表

表1中Ⅰ类型钢锚固方式为在型钢腹板焊接栓钉的锚固方式，Ⅱ类型钢锚固方式为在型钢翼缘焊接栓钉的锚固方式。栓钉尺寸及具体形式见图1，栓钉布置间距为200 mm。此外，所有试验梁的上、下翼缘之间按一定间距焊接HRB400级钢筋，既起到箍筋的作用，又可作为梁的抗剪连接件。

在型钢骨架完全加工好后，将钢绞线穿入需要施加预应力的试件骨架并进行预应力张拉，张拉过程中采用一端固定、一端张拉的方式。待钢绞线预应力损失基本稳定后浇筑自密实混凝土。混凝土养护完毕后将试件侧面用打磨机打磨平整。

预应力部分外包钢组合梁各试件尺寸如图1所示。

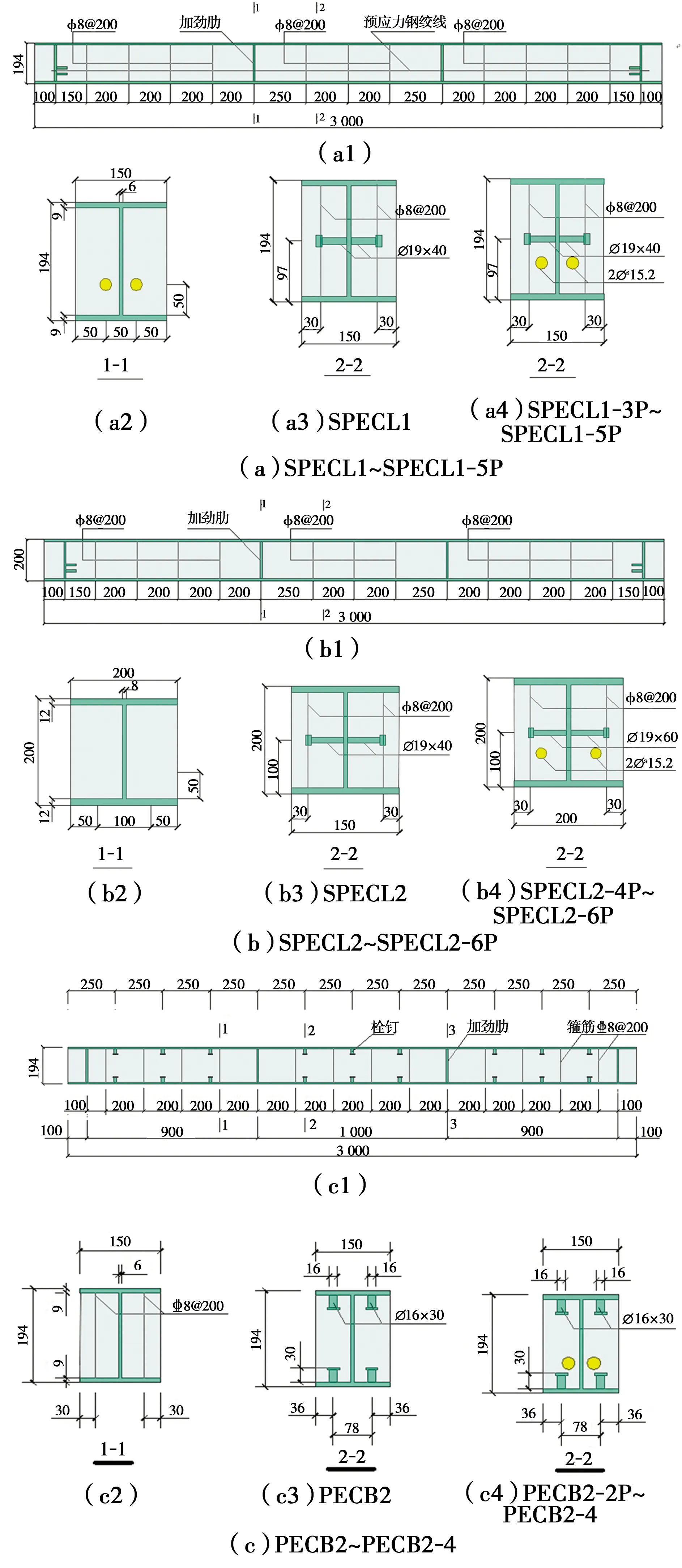
图1 各试件尺寸示意

1.2 材料性能

在试验开始前，需要对主要试验材料进行材性试验，按《混凝土结构试验方法标准》[18]中的规定对钢筋、型钢与预应力钢绞线以及混凝土试块进行材性试验，钢筋、型钢与预应力钢绞线力学性能指标如表2所示，混凝土力学性能指标如表3所示。

表2 钢材力学性能指标

表3 混凝土力学性能指标

1.3 测点布置

试件的竖向位移、横筋、跨中型钢腹板与上下翼缘板以及混凝土的应变情况为试验测量主要内容。试件位移计与应变片布置见图2，沿截面高度方向粘贴的应变片均为等间距粘贴。

图2 试件位移计与应变片布置示意

1.4 加载方案

试验在广西科技大学结构试验室进行，使用量程为1 000 kN的液压千斤顶装置进行加载，通过电动油压泵进行控制。试验所用力传感器放置在液压千斤顶与分配钢梁之间。试验荷载利用长度为1.7 m的分配钢梁进行二等分，再通过柱铰传递给试验梁，试验加载装置示意见图3。

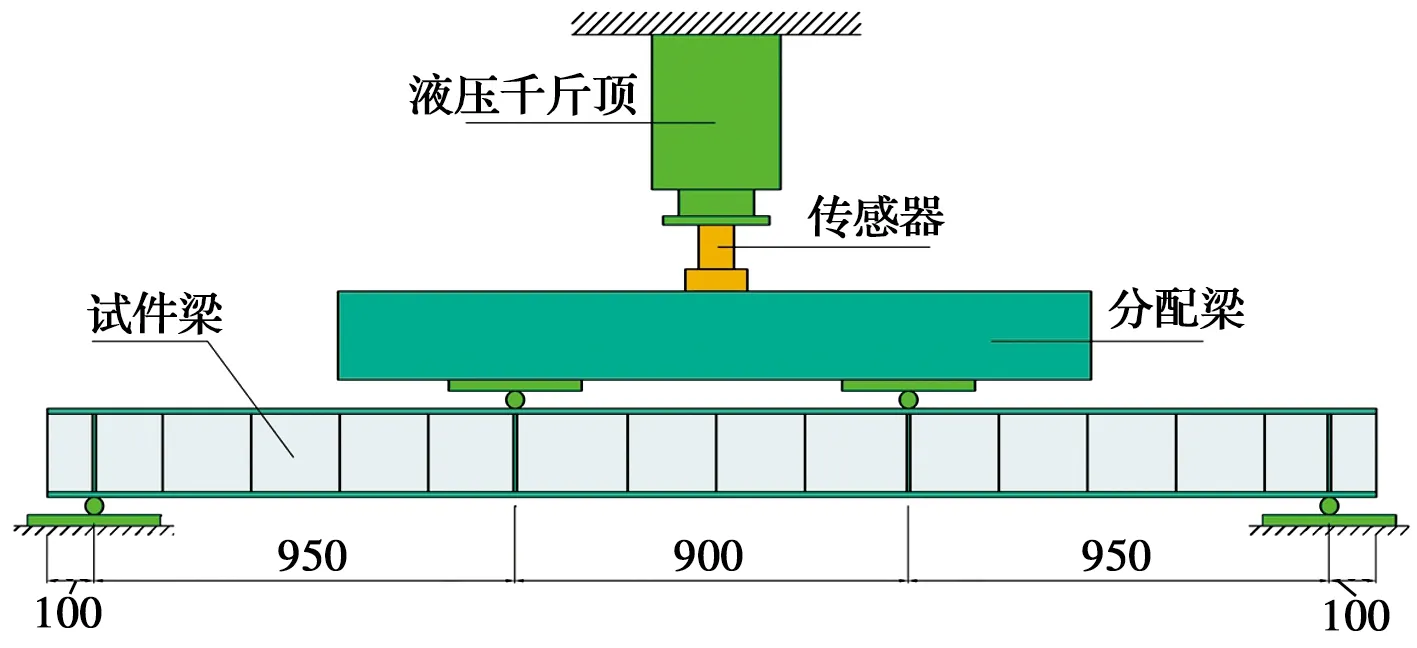
图3 试验加载装置示意

在试验前，需对试验梁进行预加载，在检查各个试验仪器工作情况以及试验梁的稳定性良好后进行正式加载。在试验梁开裂之前，按每级所加荷载为5%的计算极限荷载进行匀速加载，每级持荷10 min。在试验梁开裂后，每级所加荷载为计算极限荷载的10%，每级持荷10 min。当荷载值达到试验梁计算极限荷载的80%时，每级加载速度放缓至计算极限荷载的5%，直至荷载不再增加，并降为极限荷载的85%时，试验梁破坏，开始缓慢卸载。试验过程中产生的所有数据均通过JM3813多功能静态应变采集仪自动收集。

2 裂缝开展分析

2.1 裂缝开展情况

所有试验试件最终破坏形态如图4所示。由图4可知，所有试件破坏模式均为弯曲破坏，且破坏过程亦大致相同。在加载初期至试件屈服荷载前，试件竖向变形并不明显，试件达到屈服荷载后，在加劲肋处裂缝开展较快，试件产生肉眼可见的竖向变形，随着荷载的继续施加，裂缝也持续向上开展，过程中伴随着混凝土掉渣现象。当试件接近极限荷载时，试件跨中上部受压区混凝土已被严重压碎，型钢翼缘板变形起皮，从混凝土部分剥离，直至试件破坏。在整个加载过程中，所有试件均未发生面外失稳现象。此外，预应力部分外包钢组合梁SPECL1-3P、SPECL1-4P、SPECL1-5P、SPECL2-4P、SPECL2-5P、SPECL2-6P、PECB2-2、PECB2-3与PECB2-4相较于各自的对照组SPECL1、SPECL2与PECB2其开裂荷载均有明显提高，且施加预应力后裂缝分布较为均匀，可见，预应力筋的设置对裂缝开展起到了很好的抑制作用。对比SPECL1、SPECL1-3P、SPECL1-4P与SPECL1-5P可知，当预加压力较大时，试件加劲肋板附近混凝土易产生相对较大的长裂缝。其原因可能是加劲肋板与其附近混凝土之间并未设置抗剪装置，导致二者间的结合处抗剪能力薄弱，当预加压力较大时，该位置在破坏时会呈现出类似脆性破坏状态，裂缝发展较其他位置更为明显。所有试件在破坏之前征兆明显，总体上具有较好的塑性性能，并且在较大的荷载作用下稳定性良好。

图4 各试件最终破坏形态

2.2 分形维数评价

通过引入分形维数来评价试件破坏时的裂缝开展情况。分形维数是评价几何图形分形特征的重要参数，表示几何图形局部与整体的相似程度[19]。分形维数的确定方法主要有标尺法(Ruler method)，盒计数法(Box method)及分岛法(Slit island)[20-21]。为定量评估构件表面裂纹的分形特征，采用计盒法计算裂缝的分形维数。计盒法的操作过程为：取边长为r的方盒覆盖全梁，统计内部含有裂缝的方盒数量记为N(r)，缩短方盒边长并重复以上过程，最终获得一系列的(r，N(r))数据。拟合lnr-lnN(r)曲线，如果得到的曲线为线性相关的直线，则证明裂缝具有分形特征，裂纹的分形维数为

Df=lnN(r)/lnr

(1)

使用计盒法求解结构的分形维度需要预先确定方盒的尺寸范围，尺寸的上限为裂纹间距，下限为骨料最大粒径[22]。试验混凝土中骨料的粒径为5～30 mm，上限取裂纹平均间距，90 mm[23]。因此，方盒尺寸分别为30、40、50、60、70、80、90 mm。破坏状态下所有试件lnr-lnN(r)关系曲线如图5所示。

图5 各试件ln r-ln N(r)关系曲线

由图5可知，在破坏状态下，各试件表面裂缝在给定的网格尺寸范围lnr-lnN(r)内存在较好的线性关系，说明在一定标度范围内预应力部分外包钢组合梁的表面裂缝分布满足统计意义上的分形特征，所有构件表面裂缝的分形维数如表4所示。

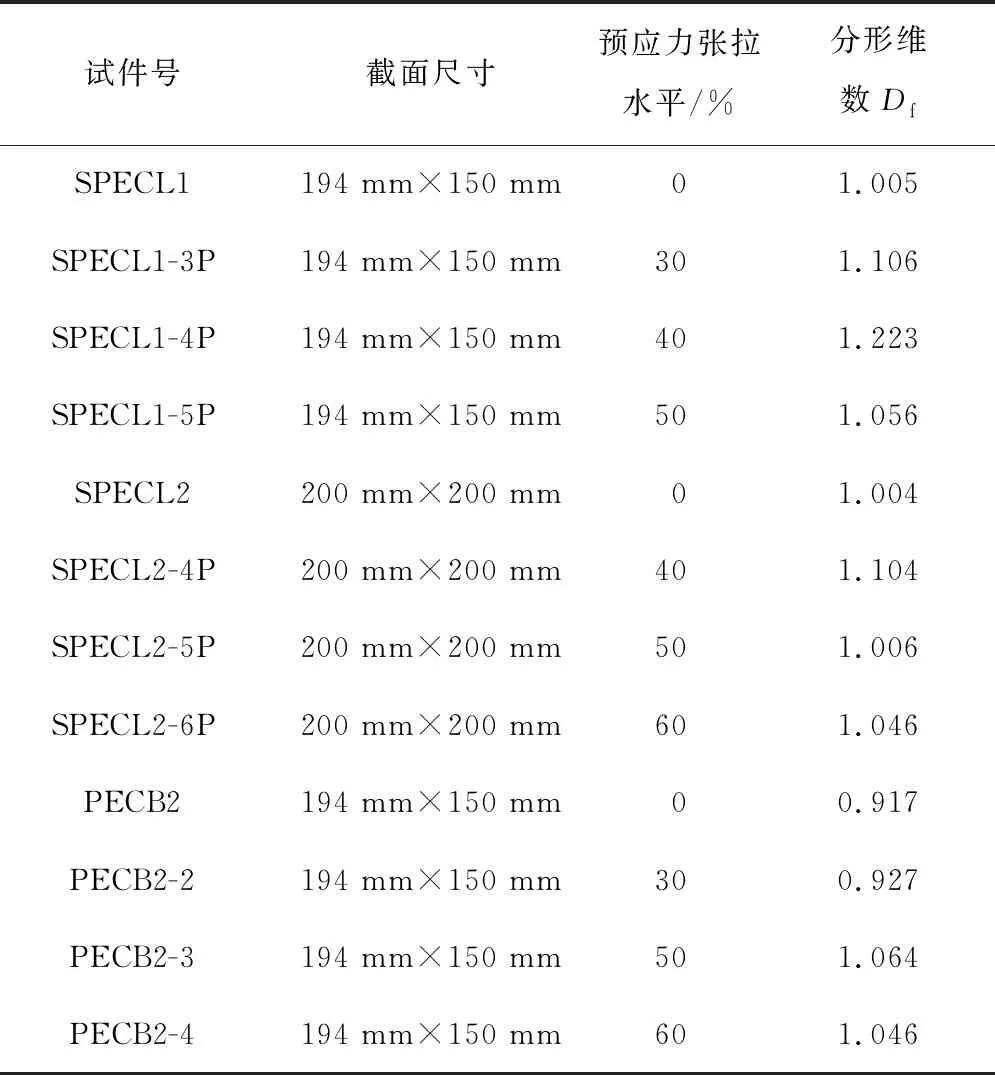
表4 各试件分形维数

对比试件SPECL1与试件SPECL2，由表4可知，相同预应力张拉水平下的试件SPECL2比试件SPECL1的分形维数略小或近似相同，说明试件截面尺寸的改变对试件裂缝开展的影响不大。对比试件SPECL1与试件PECB2可知，试件PECB2的分型维数较试件PECL1下降了8.7%，说明Ⅰ型型钢锚固方式下的试件梁比II型型钢锚固方式下的试件梁裂缝开展更充分一些。原因可能是采用腹板焊接栓钉的Ⅰ型型钢锚固方式平均黏结强度更大一些[24]，故混凝土与型钢的结合受力情况更协调。对比试件SPECL1、试件SPECL1-4P、试件SPECL1-5P与试件SPECL1-6P的分形维数可知，预加一定程度的预应力可使试件在破坏时的裂缝开展更充分，但当施加的预应力较大时，其分形维度反而会有所下降。说明较大的预应力对试件的开展帮助不大，原因可能是对梁内混凝土施加较大的预压应力会导致梁内混凝土的延性下降，脆性增加，梁内混凝土产生较为集中的细长裂缝而非分布范围较广的中小裂缝。故可认为在某一特定范围内的预应力张拉水平对预应力部分外包钢混凝土梁试件的破坏现象有一定影响。

3 挠度分析

3.1 荷载-挠度曲线

各试件的荷载-挠度曲线如图6所示。对比SPECL1、SPECL2与PECB2可知，改变试件截面尺寸与型钢锚固方式对试件承载力和竖向变形均产生明显影响。以SPECL1系列为例，对比SPECL1、SPECL1-3P、SPECL1-4P与SPECL1-5P可知，施加预加压力对试件承载能力有所提高，但影响有限；对试件抵抗竖向变形的能力则影响较为明显，但亦有随着预加压力的提高，最大挠度变形反而下降的趋势。综上所述，3种影响因素均为预应力部分外包钢组合梁试件挠度变化的重要影响因素。

图6 试件荷载-挠度曲线

3.2 短期刚度推导

《混凝土结构设计规范》[25](以下简称规范)提出了关于允许出现裂缝构件的短期刚度基本公式，在此公式的基础上进行修改，考虑型钢对试件刚度的贡献，提出预应力部分外包钢组合梁的短期刚度基本公式，见式(2)～式(12)。

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

Mcr=(σpe+γftk)W0

(10)

(11)

(12)

式中：Aa、Ac、Ap分别为试件截面型钢与混凝土面积，mm2；Ea、Ec、Ep分别为试件截面型钢与混凝土弹性模量,MPa；I0为开裂前试件截面换算惯性矩,mm4；x0为截面受压区高度,mm；epn为净截面重心至预应力钢筋的距离,mm；Mk、Mcr分别为计算区段内的最大弯矩值与开裂弯矩值,kN·m；β0.4、βcr分别为Mcr/Mk=0.4、0.6时的刚度降低系数，βcr依然按规范取值0.85；ρ为型钢与预应力筋综合配筋率，式中α1依然按规范后张法预应力筋取值为1；γf为受拉翼缘截面面积与腹板有效截面面积的比值；σpe为有效预压应力,kN；Npe为试件有效预压力,kN；γ为混凝土构件的截面抵抗矩塑性影响系数，式中γm依然按规范取矩形截面值1.55；In为静截面惯性矩,mm4；yn为净截面重心至受拉型钢边缘的距离,mm；ftk为混凝土轴心抗压强度标准值，N/mm2；W0为截面抵抗矩,mm3。此外，式(6)中的C为参照规范形式下的调整系数，通过与短期刚度试验值拟合的方式进行取值，最终取值为-0.25。

根据《规范》中受弯构件短期刚度的截面刚度与曲率的理论关系式来计算所有试件短期刚度试验值，见式(13)。

(13)

分别求出各试件试验值与理论计算值，将各试件短期刚度的试验值与理论计算值进行比较，结果见表5。两者最大偏差发生在试件PECB2-4，为19%。分析原因可能为试件PECB2-4在应变监测部位附近的混凝土存在缺陷，导致在加载过程中试件下侧型钢拉应变过大，致使其短期刚度试验值低于理论计算值。所有试件刚度平均偏差约为7%。从比较结果来看，上述公式计算出的预应力部分外包钢短期刚度值表现出较好的精确性。

表5 各试件短期刚度理论值与试验值比较

续表5

3.3 基于两种理论下的挠曲线方程

组合梁试件的挠曲线方程可以反映试件在竖向加载作用下的整体变形情况，为寻求更加精确与相对简便的梁挠曲线方程，采用Euler梁理论与Timoshenko梁理论分别构建该结构的挠曲线方程，并以跨中挠度值作为判定标准，通过将两种理论下的梁跨中挠度计算值与试验值进行比较，得出最接近试验值的计算理论。

3.3.1 基于Euler梁理论的试件挠曲线方程 Euler梁理论又称经典梁理论，此理论在计算梁的挠度时忽略了横向剪力和横向正应变的影响，形式简单、实用，在长梁试件中应用广泛。根据图2所示加载示意图，在纯外载荷作用下的梁弯矩方程如式(15)所示。

(15)

式中：F为试件屈服时加载点竖向加载值；l1与l2分别为试验梁弯剪段与纯弯段间距，如图2所示，取值950、900 mm。

在Euler梁理论下梁的挠曲线基本微分方程为

(16)

由于试件在正常使用荷载状态下需使用短期刚度，因此，式(16)中的EI需替换为短期刚度Bs。求解微分方程并带入边界条件可得Euler梁理论下的试件挠曲线，Euler梁挠曲线方程见式(17)。

由于预应力筋对试件梁的反拱作用会对试件整体挠度产生一定程度影响[26]，试件梁挠曲线方程还需叠加由预应力筋产生的挠度Δf，Δf见式(18)。

(18)

Mp=-Npeep

(19)

Npe=2σpeAp

(20)

式中：l为试件总长度；α为刚度折减系数，依据各试件试验真实挠度值，采用文献[27]中的公式并取平均值，见式(21)。

(21)

实际上，由于自重也会使梁产生一定的挠度，即自重挠度fG，自重挠度fG计算式为

(22)

故预应力部分外包钢组合梁的挠度公式为

fE=f+Δf+fG

(23)

该理论下的梁跨中挠度计算式为

(24)

3.3.2 基于Timoshenko梁理论的试件挠曲线方程 在Euler梁理论中，计算梁的挠度时仅考虑了梁弯曲变形的影响，但Timoshenko认为梁的挠度除受弯曲变形的影响，梁内截面的剪切变形也会对梁产生附加挠度[28]，若用fs表示仅由剪切作用所引起的挠度，其基本表达式为

(25)

(26)

式中：G1为组合梁截面剪切弹性模量，按式(26)进行计算；Gc与Ga分别为混凝土剪切模量与型钢剪切模量；αs为剪切系数，矩形截面取1.5。

求解此微分方程可得

(27)

故依据Timoshenko梁理论，预应力部分外包钢组合梁的挠曲线基本方程为

fT=f+Δf+fG+fs

(28)

该理论下的预应力部分外包钢组合梁跨中挠度计算式为

(29)

3.4 两种理论下的跨中挠度比较分析

将两种理论下试件屈服阶段跨中挠度试验值与挠度计算值进行比较，结果如表6所示。

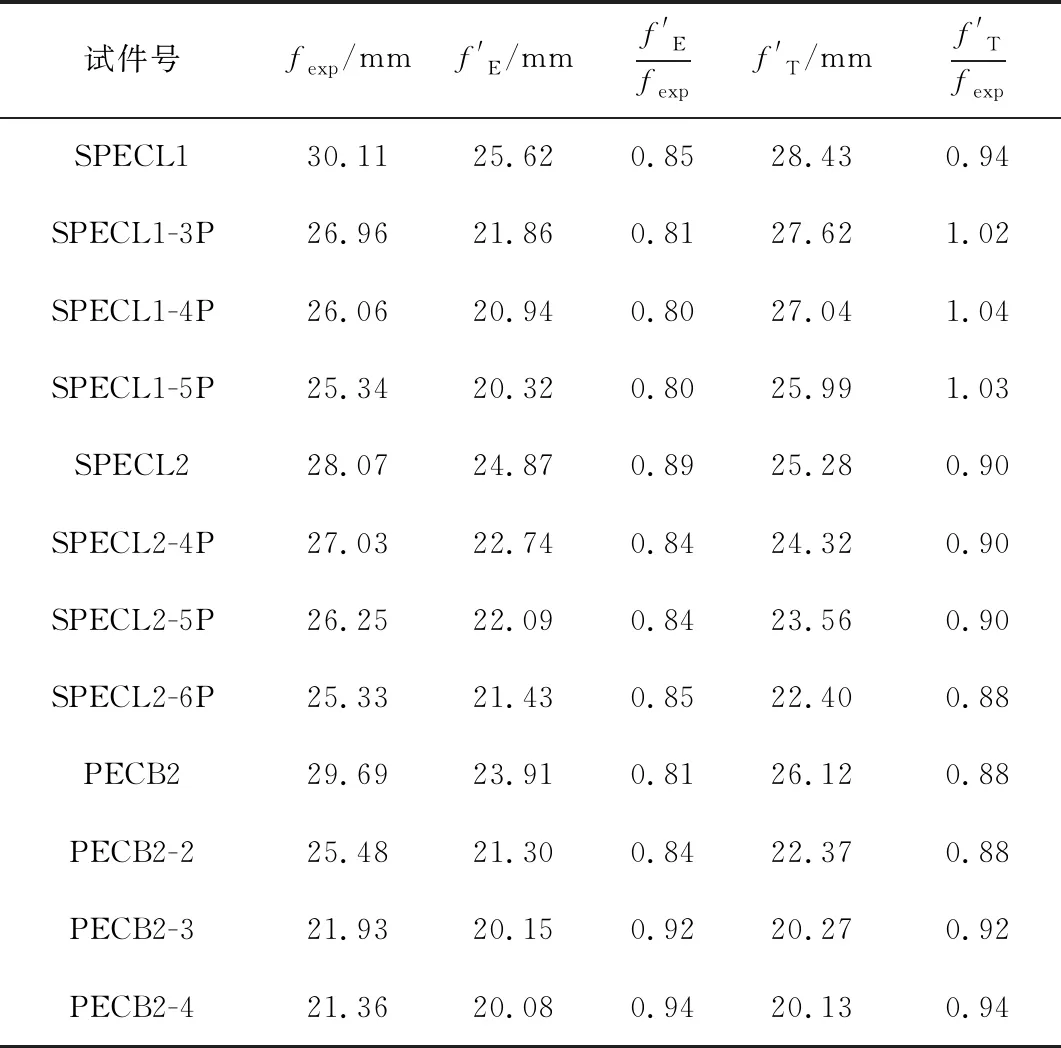
表6 各试件跨中挠度理论值与试验值比较

依据表6中的数据计算两种理论值与试验值的方差大小，其中Euler梁理论值的方差约为17.87，而Timoshenko梁理论值的方差仅为5.19。由表6可以看出，Timoshenko梁理论计算出的各试件跨中挠度值均稍大于Euler梁理论下的跨中挠度计算值，也更加接近试验值，故在计算预应力部分外包钢混凝土梁的跨中挠度时，建议采用Timoshenko梁理论进行该结构在屈服荷载下的跨中挠度计算。

4 延性分析

4.1 3种延性系数计算与比较

延性是指构件或构件的某个截面从屈服开始到达最大承载能力或到达以后而承载能力还没有明显下降期间的变形能力。在工程中常用延性系数来定量描述构件的延性。常用的延性系数主要有位移延性系数、曲率延性系数与能量延性系数[29]。其中，位移延性系数与能量延性系数能够反映构件整体的延性性能，而曲率延性系数则能反映对应截面处的截面延性。为探求预应力部分外包钢组合梁的延性性能，将各试件位移延性系数、曲率延性系数与能量延性系数分别进行计算，并对3种延性系数进行比较。3种延性系数的计算公式如式(30)～式(32)所示。

(30)

(31)

(32)

式中：fy为试件屈服时跨中挠度值；fs为试件跨中最大挠度值；(1/ρ)y为试件屈服时跨中曲率值；(1/ρ)s为试件跨中最大曲率值；Epl为试件塑性能；Eel为试件弹性能；Epl与Eel可通过各试件的位移-荷载曲线所包围的面积取得，试件弹性能与塑性能示意图如图7所示。

图7 弹性能与塑性能示意

各试件位移延性系数、曲率延性系数与能量延性系数对比如表7所示。由表7可知，各试件的位移延性系数与能量延性系数的变化趋势基本相同，在预应力张拉水平不太大时，各试件的延性系数随预应力的增大而增大，但当预应力张拉水平超过某一界限时，其延性系数反而有所减小。其原因可能是较大的预压应力使试件储存了较多的弹性能，限制了试件的裂缝开展，且在试件逐步开裂的过程中因裂缝开展不充分导致其应力在重分布时分布不均衡，在破坏时试件沿最大裂缝处产生弯曲破坏，最终导致试件脆性增加，延性减少。综合试件的试验结果，建议此结构的预应力张拉水平以不超过40%为宜。同时通过表7可知，当试件的试验参数改变时，能量延性系数相较位移延性系数的波动更明显些，因此，在对不同预应力部分外包钢组合梁的整体延性性能进行分析时，推荐采用能量延性系数进行评价与比较。

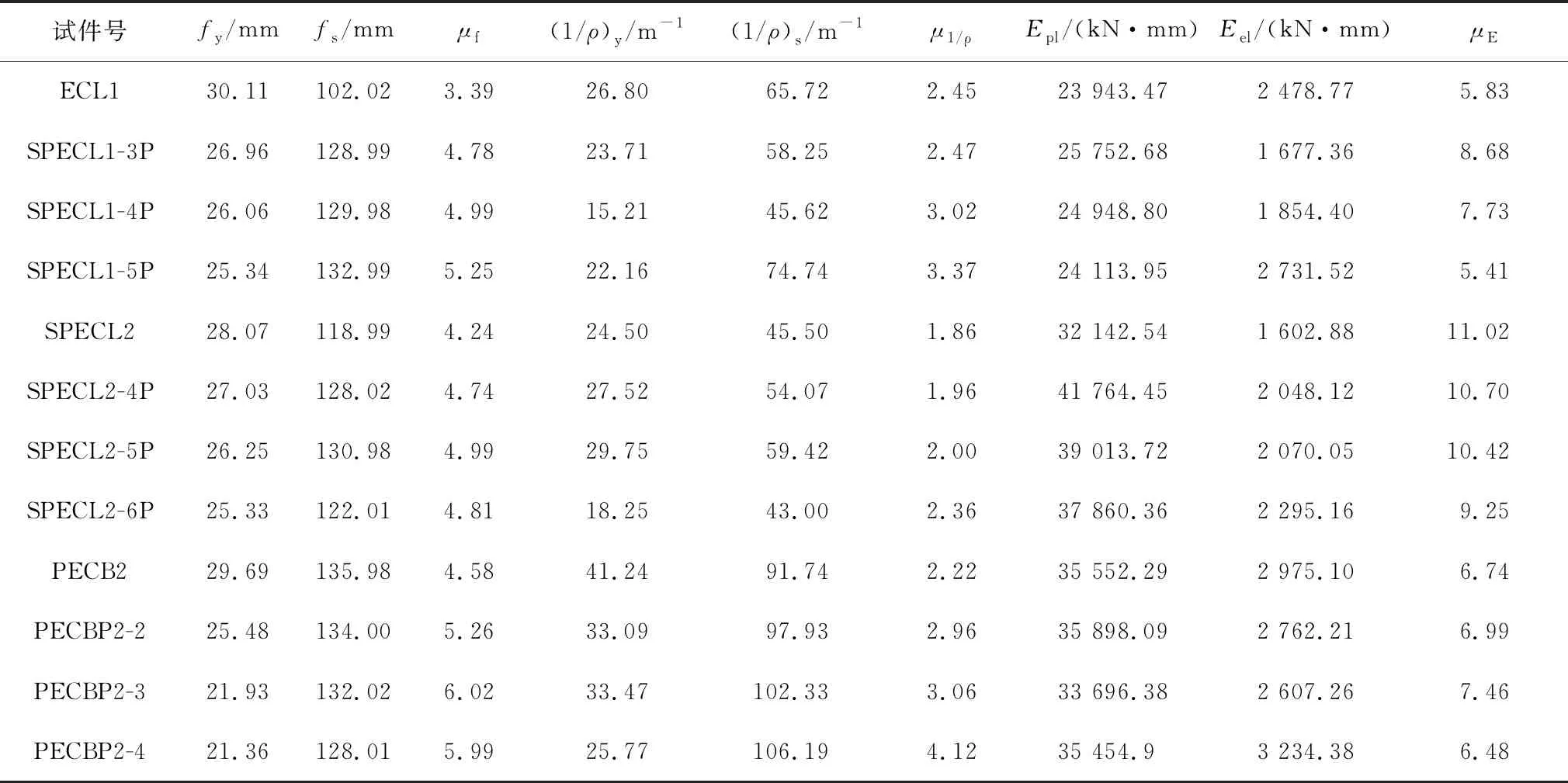
表7 各试件延性系数对比表

分析各试件的跨中截面曲率延性系数可知，试件的曲率延性系数基本呈现出随截面尺寸的增大而减小、随预应力张拉水平增大而增大的趋势。说明预应力张拉水平的提高以及增加试件梁的截面尺寸均有利于对预应力部分外包钢组合梁试件的跨中截面延性的提高。对比SPECL1与PECB2，PECL1-5P与PECBP2-3可知，锚固形式的改变对试件跨中截面曲率延性系数的影响不大。

4.2 基于灰度关联法的影响因素分析

灰度关联分析法是一种根据因素间发展趋势的相异程度来确定彼此间的关联程度大小的影响因素分析方法，主要应用于研究“少数据不确定性”问题[30]。由于此方法对样本量的大小没有太高要求，恰好适合试验的影响因素分析。

依据表8中的各试件影响因素参数，对各试件位移延性系数、曲率延性系数与能量延性系数分别进行关于截面面积、预应力张拉水平与型钢锚固方式的参数影响因素分析。具体计算步骤如下：

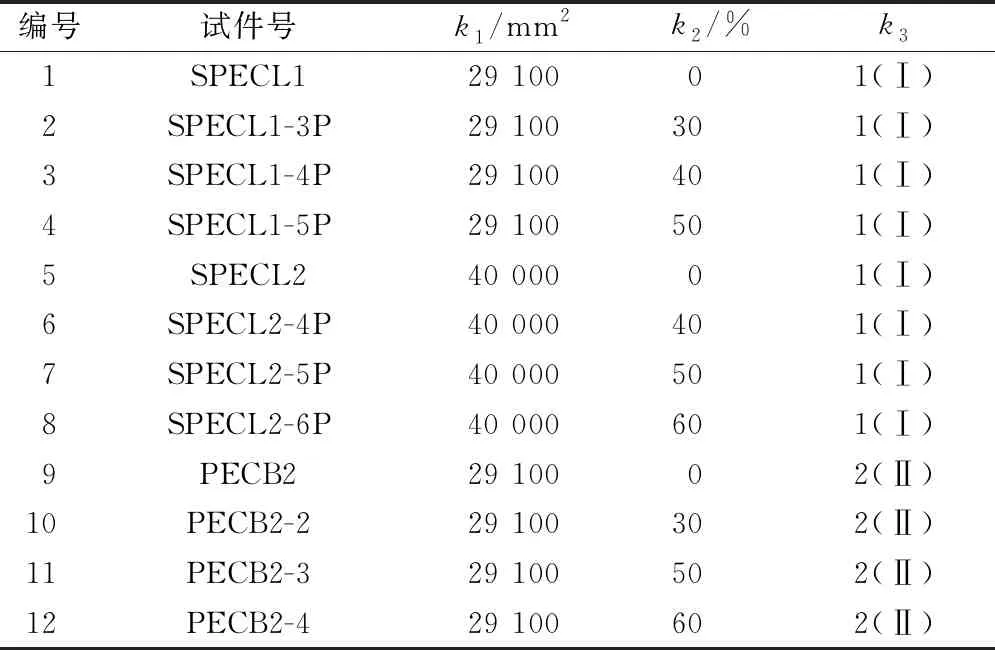
表8 各试件影响因素参数表

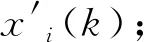
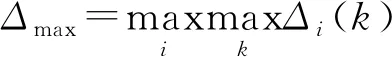
各试件分析结果见表9。由表9可知，试件截面面积、预应力张拉水平与型钢锚固形式3种参数对于位移延性系数的关联度值分别为0.75、0.66与0.61；对于曲率延性系数的关联度值分别为0.80、0.61与0.63；对于能量延性系数的关联度值分别为0.53、0.62与0.67。依据灰度关联分析结果，表明试件截面面积对试件位移延性系数与曲率延性系数的影响程度最深，而型钢锚固形式则能显著影响各试件的能量延性系数。

表9 各试件3种延性系数影响因素分析

5 结论

1)对预应力部分外包钢组合梁进行基于分形维度理论下的裂缝开展情况分析，结果表明，各试件裂缝开展情况满足统计意义上的分形特征，且施加一定程度的预压应力与型钢腹板焊接栓钉的锚固方式对该结构的裂缝开展情况影响较大。

2)依据试件试验结果进行基于Euler梁理论与Timoshenko梁理论的预应力部分外包钢组合梁的挠曲线方程推导，并对两种理论下的跨中挠度计算值与试验值进行比较，认为基于Timoshenko梁理论计算出的跨中挠度值更接近试验值。

3)对各试件进行关于位移延性系数、跨中曲率延性系数与能量延性系数的计算与分析，结果表明，增大试件截面尺寸与在一定范围内提高试件的预应力张拉水平均可改善预应力部分外包钢组合梁延性。

4)对试件3种延性系数进行基于截面尺寸、预应力张拉水平与型钢锚固方式的灰度关联法分析，分析结果表明，试件截面面积对试件位移延性系数与曲率延性系数的影响程度最深，型钢锚固形式对能量延性系数的影响系数最深。