大型储罐顶部抗风圈设计方法对比和优化*

倪恒 陈严飞，2 马尚 董绍华

1中国石油大学（北京）·油气管道输送安全国家工程实验室·城市油气输配技术北京市重点实验室

2大连理工大学·工业装备结构分析国家重点实验室

储罐大型化是当前储罐发展的趋势[1]，但容积越大的储罐抵抗风载荷的能力越差，而我国原油储库大多坐落在沿海地域，储库中的大型储罐易在台风等极端天气的作用下屈曲失稳（图1），故需对储罐的抗风能力进行加强。目前主要采用加大壁厚和增设抗风结构两种方法，其中，单纯通过增加储罐壁厚的方式来提高屈曲载荷因钢材成本和焊接工艺等因素受到限制[2]，而在储罐罐壁中上部增设抗风圈较前者可以在原有壁厚的基础上提高储罐的抗风性能，故抗风圈的合理设计与安装显得尤为重要。

图1 储罐在飓风下的整体屈曲Fig.1 Overall buckling of the tonk under the hurricane

我国大型储罐抗风圈设计通常参照GB 50341设计规范以及美国石油学会API 650 设计规范，上述两种规范中抗风圈的设计方法存在差异[3]，国内一些学者认为，相较于API 650 设计规范，使用GB 50341 设计的大型储罐抗风圈更为保守。李玉坤[4]使用有限元模拟软件对储罐强度和稳定性进行仿真分析，认为使用API 650 设计的抗风圈更加稳定且节省材料。李良平[5]在比较了GB 50341 和API 650 标准之后，认为使用API 650 标准设计的抗风圈具有更好的经济效益。GB 50341 设计方法过高的保守性导致抗风圈设计尺寸偏大，抗风圈性能没有得到充分利用，李宏斌[6]建议参考API 650 以及BS 2654 的抗风圈设计规定，当储罐实际直径大于60 m 时，抗风圈截面模数计算公式中的设计直径仍按照60 m 进行计算，能起到节省钢材和方便施工的作用。李玉坤和孙文红[4]建议将我国规范中抗风圈截面模量公式中的风载荷标准值替换为基本风压以降低其保守性，这条建议在GB 50341—2014中得到了采纳。此外，国外学者针对抗风圈设计也展开了相关研究，BRIASSOULIS 和PECKNOID[7]对三个风载荷作用下的加强筒仓进行分析后指出，罐壁和抗风圈之间的相互作用会产生较大的周向应力。BU 和QIAN 认为[8]，API 650 中所采用的二维简化力学模型没有考虑底部约束的加强效果，导致大型储罐抗风圈过于保守。

大多数学者经实验观测及理论分析后认为，现有规范中大型储罐抗风结构设计方法过于保守，需提出合适的方法降低保守性。针对此问题，本文参考API 650 规范中降低保守性措施开展对GB 50341抗风圈截面模量计算公式中设计直径上限的研究，对顶部抗风圈设计方法提出了优化的建议，并建立有限元模型进行屈曲分析加以验证。

1 现行规范顶部抗风圈设计方法

1.1 GB 50341 设计方法

GB 50341 选用的简化力学模型特征为：储罐只有迎风面中心子午线周围的60°区域受风载荷作用；作用于罐壁的风压大小符合正弦分布且方向垂直于罐壁表面。储罐受风载荷作用问题便简化成为了一个圆拱段在方向受正弦分布外力作用的平面问题，简化力学模蓴如图2 所示。

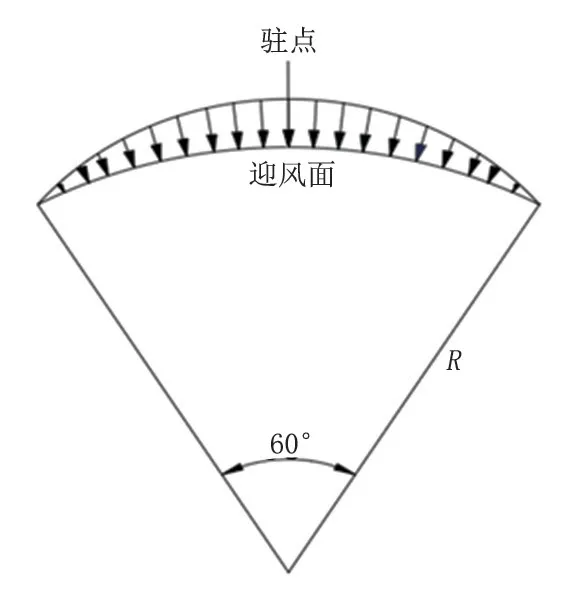
图2 GB 50341 简化力学模型Fig.2 Simplified mechanical model of GB 50341

假设储罐上部承受的风载荷全由抗风圈承担，最大弯矩出现在圆拱中心（驻点位置），其大小为

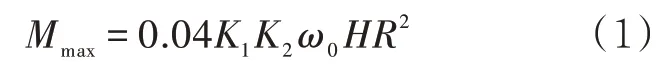
式中：Mmax为最大弯矩，N·m；K1为体型系数，取1.5；K2为风压高度变化系数，取1.15；ω0为基本风压，Pa；H为储罐高度，m；R为储罐半径，m。

最小截面模量计算公式为

式中：Z为顶部抗风圈最小截面模量，mm3；[σ]为材料的许用应力，取210 MPa。

合并公式（1）、（2），代入相关数据并向上取整后得到与基本风压值，储罐几何尺寸相关的最小截面模量计算公式为

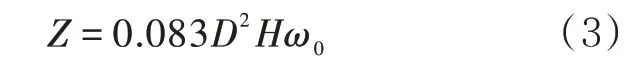
式中：D为储罐直径，m。

1.2 API 650 设计方法

ADAMS[9]给出了一种API 650 抗风圈尺寸设计公式的推导方法，其简化力学模型是将Roark 圆环公式中的应力情况8 和情况20 相结合（w为均布单向荷载，kPa），如图3 所示。

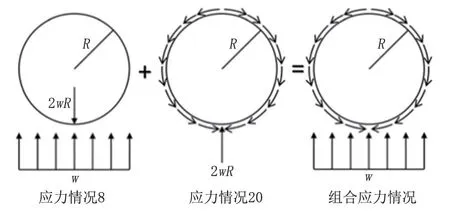
图3 Roark 圆环公式情况8 和情况20 的组合示意图Fig.3 Combination diagram of Case 8 and Case 20 by Roark ring formala

组合情况下的最大弯矩是均匀线性载荷和环半径的函数。

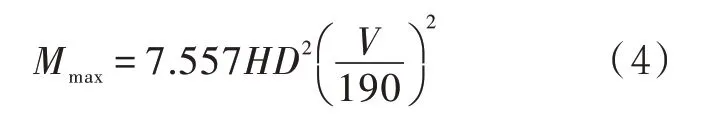
式中：V为设计风速（3 s 阵风），km/h。

抗风圈所需最小截面模量计算公式为

式中：φ为应力因子，取0.625；σ为材料的许用应力，取207 MPa。

通过上述计算得到式公（6），即最小截面模量计算公式为

1.3 两种设计方法对比

结合上述内容可以看到，API 650 和GB 50341中顶部抗风圈的设计思路相同，两种规范均使用最小截面模量来表征抗风圈尺寸，相关计算公式形式相似但具体参数不同，这主要是由基本风速（时距）以及选用的简化力学模型等因素的不同而导致的。GB 50341 使用基本风压ω0来表征风载荷的大小，而API 650 则使用设计风速V来表示，但两者本质并无区别。

从上述设计方法推导过程可以看出，两种顶部抗风圈设计方法均存在过于保守的不合理之处：GB 50341 所使用的简化模型假设风载荷仅作用于驻点周围60°内的罐壁之上，荷载大小使用正弦函数来表示，API 650 所使用的简化模型假设风载荷为单侧均布风荷载和均匀剪切荷载的结合，这些假设与储罐周围的实际风场并不一致[10-11]；API 650和GB 50341 皆要求上部罐壁的风荷载全部作用在抗风圈上，并未考虑中间加强圈和罐底对于上部罐壁的加强作用。大型储罐作为一种薄壳结构，完全忽略抗风圈、加强圈、罐底之间的相互加强作用并不合理。

API 650 规定，对于直径大于61 m 的储罐，经买家和制造商协商后，抗风圈最小模量计算公式中不需要使用储罐的实际直径，而是使用61 m 来代替。对于更加保守的GB 50341 而言，设计大型储罐顶部抗风圈时仍需要探索一种更经济的抗风圈设计直径上限。

2 顶部抗风圈设计优化

2.1 方案研究

为了降低大型储罐顶部抗风圈的保守性，提升经济性，建议使用55 m 作为GB 50341 规范顶部抗风圈的设计直径上限，采用有限元分析对其安全性进行验证，具体方案如下：

对4 个实际尺寸的储罐进行有限元建模（表1），设计顶部抗风圈时限制其最大设计直径为55 m，即对直径大于55 m 的储罐，顶部抗风圈截面模量计算公式中设计直径的取值全部用55 m 进行替代，而加强圈仍按照GB 50341 的要求进行设计。依次对4 个储罐进行线性屈曲分析和含有初始缺陷的几何非线性分析，薄壳结构具有很高的初始缺陷敏感性[12]，故只要非线性分析结果表明屈曲载荷大于设计风压，则证明储罐设计是安全的。

表1 模型储罐尺寸Tab.1 Size of model tanks

2.2 有限元模型

采用以上储罐几何尺寸对储罐建立有限元模型建立，模型罐壁厚度计算应采用变设计点法[13]，假定储罐所用板材材料为钢，模型材料杨氏模量为206 Pa(G)，泊松比为0.3。建立模型时考虑抗风圈和加强圈，顶部抗风圈的截面模量取直径55 m，各储罐顶部抗风圈设计相关参数见表2，类型为GB 50341 规范中的类型（e），截面形状如图4 所示，其中t为最上层储罐壁的厚度（mm），b为顶部抗风圈的宽度（mm）。储罐A 的加强圈尺寸（单位mm）为L200×125×12，其余3 个储罐的加强圈尺寸为L200×200×14，加强圈的位置和个数参照规范设计。有限元模型的边界条件为：储罐为空罐且不考虑罐壁附件影响；约束储罐底板的径向位移及切向位移，防止储罐发生刚体运动；施加风压载荷时仅考虑风压的周向分布[14]，但储罐迎风面、侧面、背面的风载荷分布形式直接影响屈曲载荷大小。为了有限元结果更加准确，采用RISH[15]提出的风压分布函数（公式7）模拟储罐四周的真实风压。风载荷分布示意图见图5，建立的储罐有限元模型见图6。

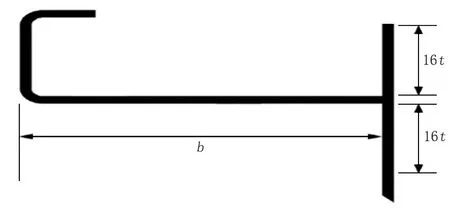
图4 设计中所采用抗风圈的截面形状Fig.4 Cross section shape of wind girder used in the design

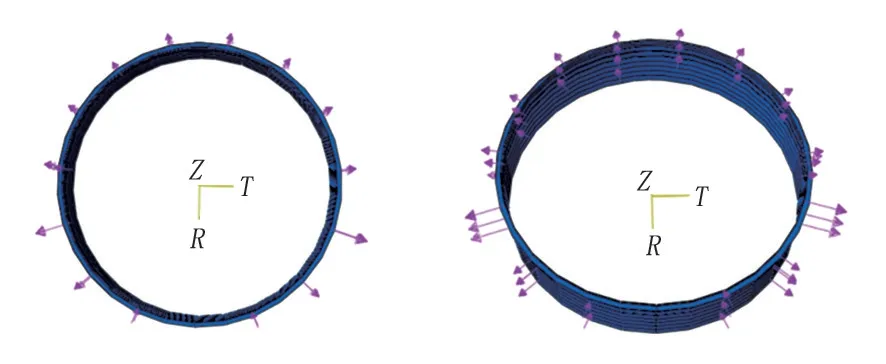
图5 风载荷分布示意图Fig.5 Wind load distribution schematic diagram

图6 储罐有限元模型Fig.6 Finite element model of tanks

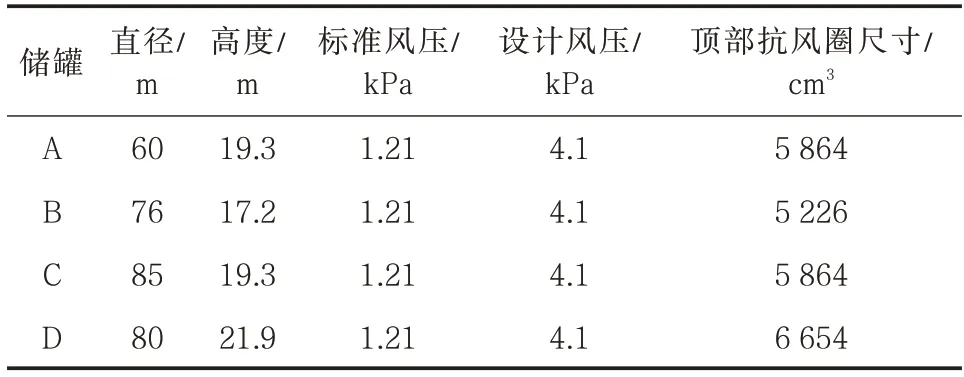
表2 顶部抗风圈设计相关参数Tab.2 Design parameter of top wind girder

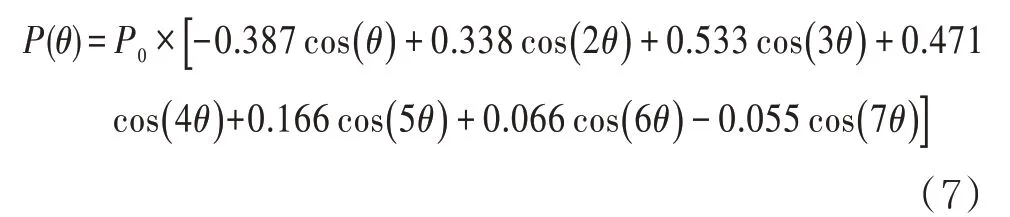
式中：θ为周向角，(°)；P(θ)为周向角θ处的风压，Pa；P0为驻点处风压，Pa。

2.3 有限元分析结果

利用屈曲分析对建立的4 个储罐有限元模型的屈曲模态和特征值进行求解，得到的结果如图7 和表3 所示。

图7 第一阶屈曲模态示意图Fig.7 First-stage buckling mode schematic diagram

表3 特征值屈曲载荷分析结果Tab.3 Analysis results of eigenvalue buckling load Pa

在特征值屈曲分析的基础上对上述储罐模型进行含初始缺陷的非线性屈曲分析，初始缺陷大小分别为0.1t，0.25t，0.5t，0.75t和1t。采用弧长法对载荷施加过程中储罐某一固定位置的载荷大小及径向位移进行跟踪，得到的载荷-位移曲线如图8 所示，图中水平轴为使用最上层罐壁厚度t归一化后的径向位移w，纵轴为使用特征值屈曲分析得到的屈曲压力载荷P(LBA)归一化后的施加载荷P，水平虚线表示特征值屈曲荷载P(LBA)，其归一化值为1.0，红色实线表示归一化后的设计压力。

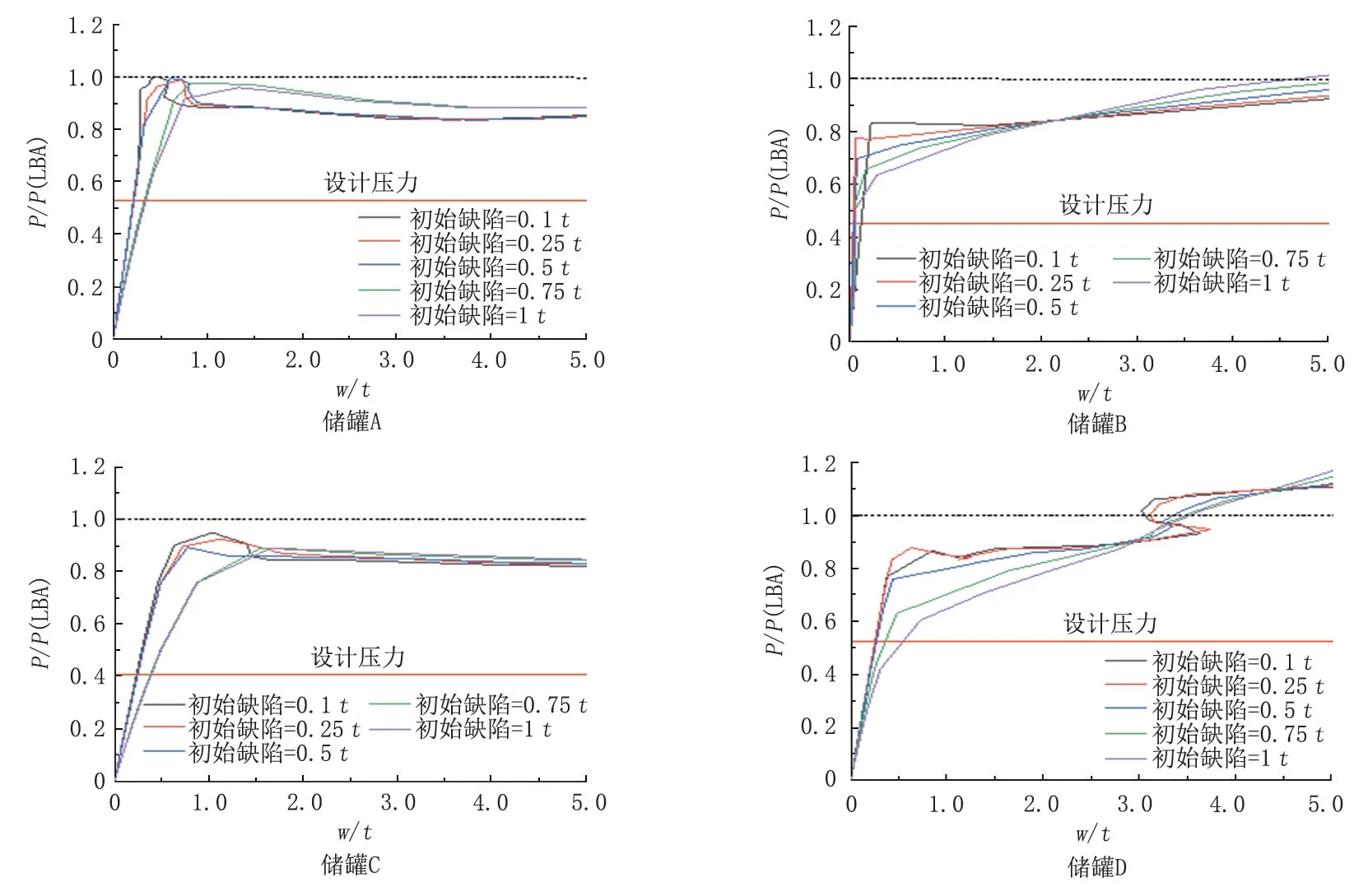
图8 含初始缺陷的非线性屈曲分析结果Fig.8 Result of nonlinear buckling analysis with initial imperfections

从图8 可以看出：在载荷施加初始阶段，随着载荷P的增大，径向位移增长较小，而后续径向位移从某点开始急剧增大，这表明储罐开始屈曲，此时该点对应的载荷P即非线性屈曲载荷。4 个储罐在不同初始缺陷下的非线性屈曲荷载都大于设计风压，这表明直径为55 m 的储罐设计的顶部抗风圈足以保持储罐顶部边缘的圆度，能有效防止储罐整体屈曲。改进后的顶部抗风圈截面模量计算公式为

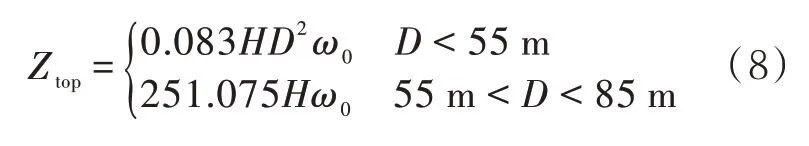
3 结论

顶部抗风圈是增强储罐抗屈曲能力的重要结构，但当前储罐设计规范中关于顶部抗风圈尺寸设计过于保守。针对此问题，阐述了两种规范中顶部抗风圈截面模量计算公式的推导过程，分析了GB 50341 和API 650 规范中不同的顶部抗风圈设计方法保守性的来源，提出了新的尺寸设计建议，并通过有限元计算进行了验证，得到以下主要结论：

（1）相较于API 650，GB 50341 关于顶部抗风圈的设计方法更加保守且缺少降低保守性的措施。

（2）GB 50341 和API 650 规范中顶部抗风圈设计保守性有两个主要来源：①简化力学模型中风荷载的分布形式与真实风压分布并不一致；②推导过程中都忽略了不同结构之间的相互加强作用。

（3）圆柱薄壳结构具有高度的缺陷敏感性，含有初始缺陷的储罐其屈曲载荷会随着引入初始缺陷比例的增大而减小。

（4）对于直径大于55 m 小于85 m 的储罐，计算顶部抗风圈截面模量时，设计直径取55 m 可以在保证安全的前提下节省储罐的建造成本。