浅析上悬窗伸缩风撑的使用

朴永日 陆赞殷

1.前言

现实生活中，幕墙上悬窗应用非常广泛，由于幕墙上悬窗的自重都比较大，所以其中的风撑一般都会采用伸缩撑—即锁定式撑档，普通的二连杆摩擦式撑档因为摩擦力不大于40N，所以无法使幕墙上悬窗定位在开启角度。

本文从力学角度出发，根据两种不同的安装比较计算，并进行了试验验证，最后得出结论。

2.计算

首先要确定模拟窗大小，确定参数条件，之后再展开分析。

2.1 应用模拟假设条件

2.1.1 开启扇定为1m×1m挂勾式上悬窗，采用6+12A+6玻璃，自重定为自重向下。幕墙开启距离按幕墙规范为300mm，则换算开启角度为17.5°。

2.1.2 风荷载标准值取为 kPa5.0 ，其风荷载均布大小为垂直于窗扇板，正负风压取值相等。

2.1.3 以目前最短的8寸伸缩风撑考虑，开启后伸缩风撑展开长度为261mm，关闭后伸缩风撑长度为205mm（展开长度是以中心距计算）；只考虑伸缩撑轴向力。（伸缩撑尺寸各五金件厂家差异不大）；伸缩撑是按一对计算。

2.1.4 以上计算均以标准值，开启工作状态下考虑，并简化所有受力不均等因素。

2.2 按伸缩撑框和扇上定位

下面按伸缩撑框上定位和扇上定位，两种情况来考虑，首先说明安装位置。很多人想当然，自己设定安装位置，但实际上是不对的。因为在确定了伸缩撑的尺寸后，它的展开长度是一定的，在悬窗开启距离确定是300mm后，它的安装位置是不能随意的。如下图1，按两种位置，框上定位和扇上定位。

从图1 可以知道，确定上悬窗尺寸及开启距离后，选择的伸缩撑尺寸一定的时候，框上定位尺寸只能在离下端360mm的位置或以上；扇上定位尺寸只能在离下端360mm的位置或以上。也就是说必须保证窗扇拉回关闭位置后，伸缩撑占据的位置长度要大于伸缩撑的名义最小长度，才能保证正常关闭。此点往往被人忽视。所以需要强调，每个不同尺寸的窗型都要先寻找伸缩撑正确的安装位置。

根据以上轨迹情况，伸缩撑开启角度按图1 可确定为30°，下面进行分析。

2.2.1 伸缩撑在框上离下端360mm处定位，如下图2。

以旋转支点O为平衡点，一对伸缩撑轴向受力为Q，可以计算如下：

1）不考虑风压时

图1 两种安装位置下8寸伸缩撑最佳位置

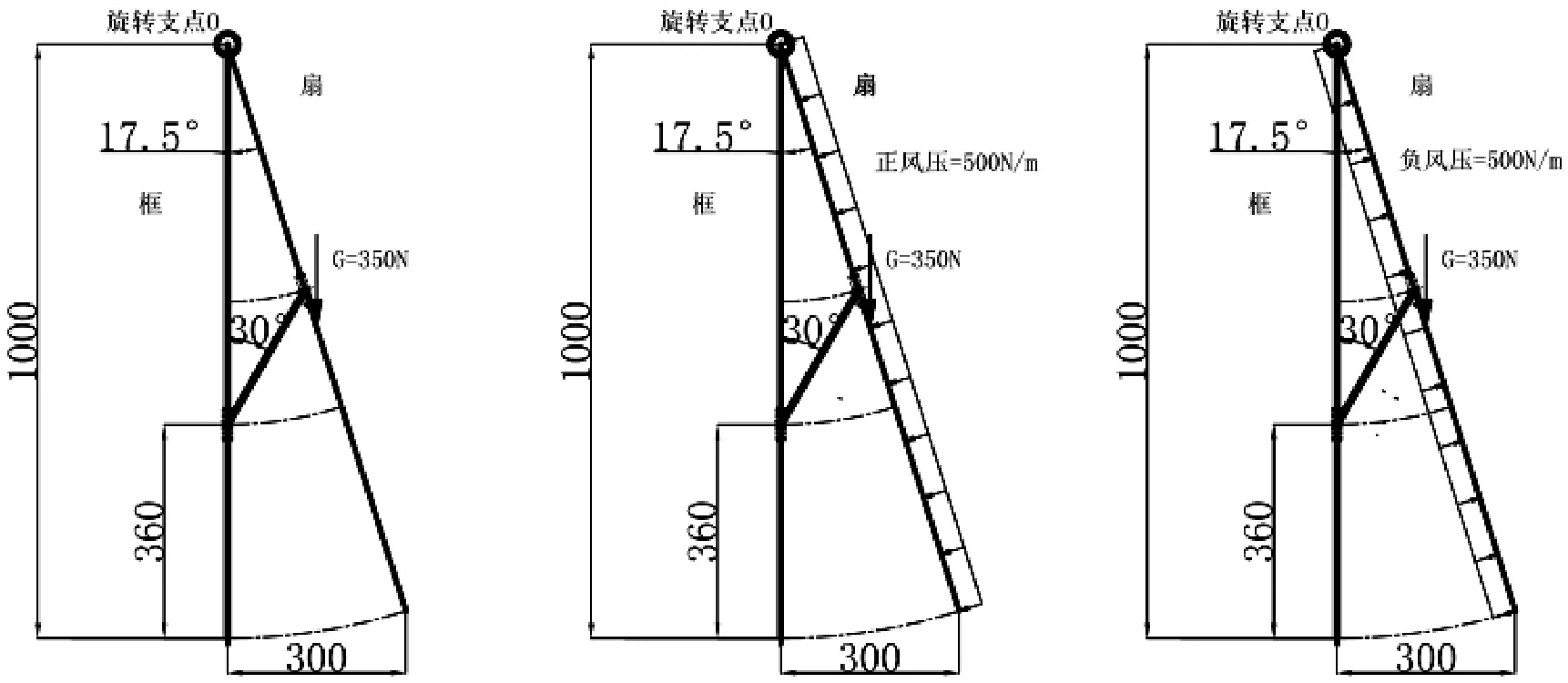
图2 伸缩撑在框上离下端360mm处定位的三种情况：从左开始，依次为无风、正风压、负风压

即不受风压时，一对伸缩撑受压力164N；

2）正风压时

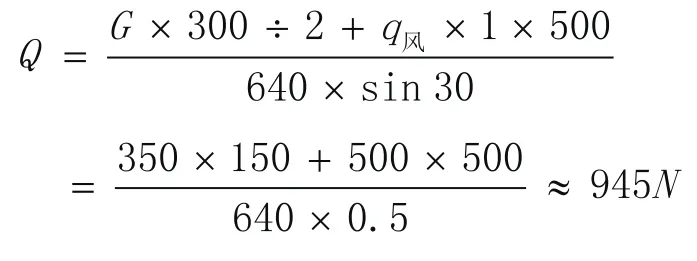
即受正风压 kPa5.0 时，一对伸缩撑受压力945N；

3）负风压时

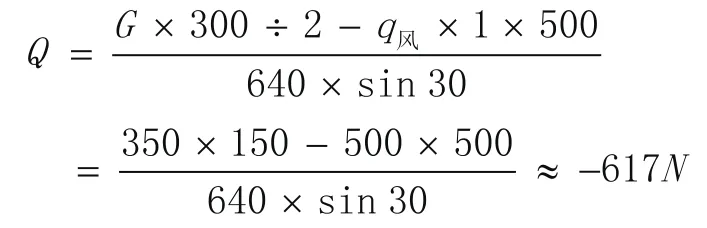
即受负风压- kPa5.0 时，一对伸缩撑受拉力617N。

2.2.2 伸缩撑在扇上离下端360mm处定位，如下图3。

同上，以旋转支点O为平衡点，伸缩撑轴向受力为Q，可以计算如下：

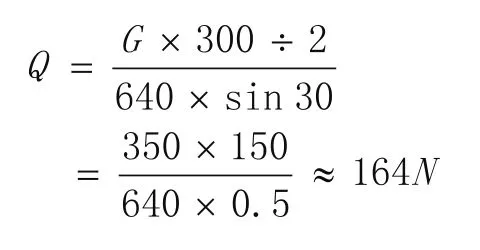
1）不考虑风压时端中点为窗扇关闭力施力位置，如图示，关闭力设为F，可以计算如下：

在平衡状态下往回关闭，实际上是要解锁伸缩撑，需将伸缩撑星形齿轮移位，所以需要先推出，使伸缩撑轴方向的力为零的过程；除了推力外，还需要克服自重的影响。

经过计算得知：

不考虑风压时，只需要克服悬窗自重，所以计算如下：

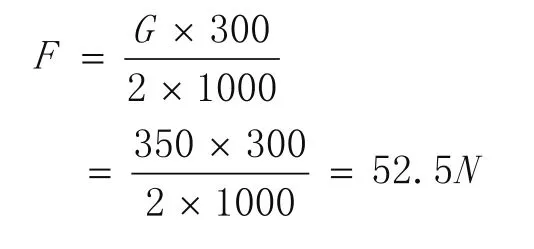
即先往开启方向施加52.5N以上的力解锁，之后会因窗扇自重影响自动回位（未考虑摩擦力）。

同理正风压时，只需要克服悬窗自重和正风压力，所以计算如下：

即先往开启方向施加302.5N力，之后因自重和正风压影响自动回位（未考虑摩擦力）。

负风压时，先要克服悬窗自重分力，而此时负风压有助于开启窗扇，往回来需要克服负风压力，所以计算如下：

伸缩撑属于锁定式撑档，单只锁定力为≥200N，假设一对伸缩撑受力均等时，先往开启方向施加力解锁推出，之后回拉，克服负风压的关闭力为197.5N（未考虑摩擦力）。

此时因为负风压以及涡流的影响，造成伸缩撑自己解锁或晃动，很容易损坏。

2）伸缩撑在扇上离下端360mm处定位，如图5。

这个道理同上，就直接说结论了。

不考虑风压时，只需要克服悬窗自重，即先往开启方向施加52.5N力，之

即不受风压时，一对伸缩撑受压力164N；

2）正风压时

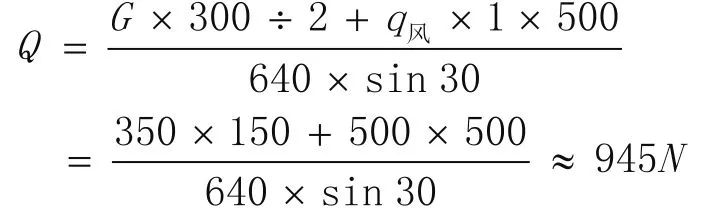
即受正风压 kPa5.0 时，一对伸缩撑受压力945N；

3）负风压时

即受负风压- kPa5.0 时，一对伸缩撑受拉力617N。

2.2.3 从平衡状态要关闭时候的关闭力：

1）伸缩撑在框上离下端360mm处定位，如下图4。

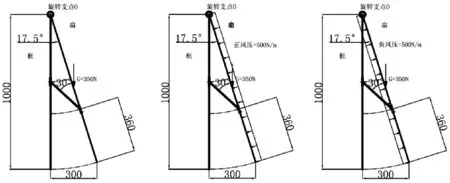
图3 伸缩撑在扇上离下端360mm处定位的三种情况：从左开始，依次为无风、正风压、负风压

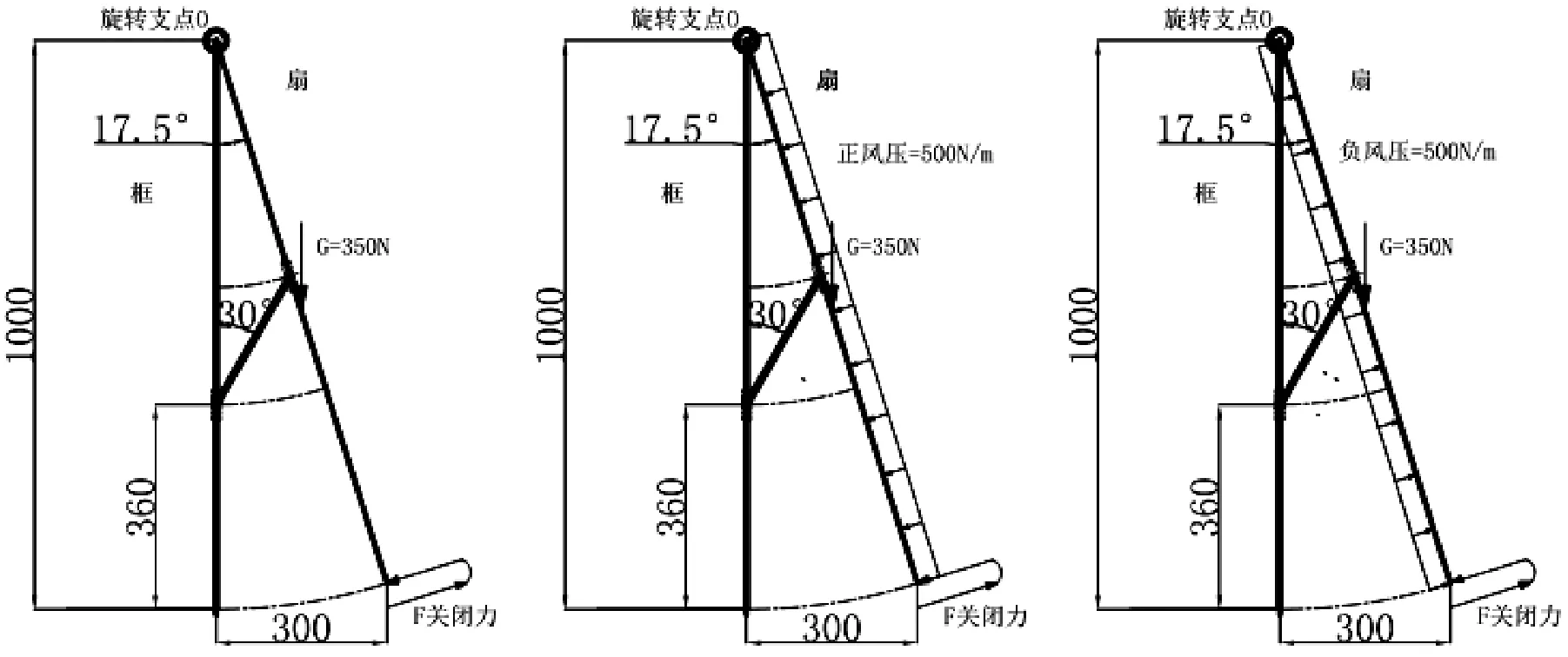
图4 伸缩撑在框上离下端360mm处定位的三种情况：从左开始，依次为无风、正风压、负风压

以旋转支点O为平衡点，窗扇最下后会因窗扇自重影响自动回位（未考虑摩擦力）。

同理正风压时，只需要克服悬窗自重和正风压力，即先往开启方向施加302.5N力，之后因自重和正风压影响自动回位（未考虑摩擦力）。

负风压时，先要克服悬窗自重，而此时负风压有助于开启窗扇，往回关闭时需要克服负风压压力，即先往开启方向施加力解锁推出，之后回拉，克服负风压的关闭力为197.5N（未考虑摩擦力）。

同理，我们很容易得出要开启窗扇到平衡状态下的开启力的情况，有兴趣的可以自己推导。

从图6受力分析，不受风压时，可以知道上悬窗一对伸缩撑的受力Q为：

从以上公式（1）可知，当我们要计算伸缩撑受力时，窗扇尺寸和重量已知，上悬窗开启角度a在开启距离固定在300mm时，也可以计算出。角度b和安装位置h就要取决于所采用的伸缩撑的尺寸。

受正风压时，上悬窗一对伸缩撑的受力为：

受负风压时，上悬窗一对伸缩撑的受力为：

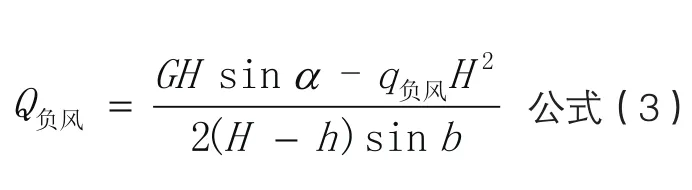
2.2.4 模拟试验窗情况：

刚性模拟窗扇：1100mm宽×1300mm高；扇重：100kg；无胶条。安装8寸伸缩风撑，设定开启距离为300mm，进行模拟试验（注：伸缩风撑开启和关闭操作时需在锁定位置向外推50mm再往回才能实现。由于测量点在开启侧距扇型材外缘 50mm处的中点上，所以需要窗高减去50mm）。

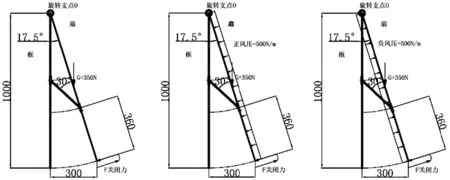
图5 伸缩撑在扇上离下端360mm处定位的三种情况：从左开始，依次为无风、正风压、负风压

图6 两个不同的安装方式时的伸缩撑受力情况

根据以上条件启闭力

1）伸缩风撑框上定位安装启闭力测试

图7 伸缩风撑安装图

图8 开启力142N

图9 关闭力142.6N

测试结果与计算结果偏差在2N左右，是因为摩擦力及其他因素影响。

2）伸缩风撑扇上定位安装启闭力测试

图10 伸缩风撑安装图

图11 开启力144.95N

图12 关闭力144.3N

测试结果与计算结果偏差在4N左右，是因为摩擦力及其他因素影响。

3）伸缩风撑框上定位安装抗破坏测试：

依据JG/T 128-2017《建筑门窗五金件 撑挡》标准，做如下试验。

图13 关闭方向施加600N/5S

图14 开启方向施加1000N/5S

根据实验数据判定结果为合格。

4）伸缩风撑扇上定位安装抗破坏测试

依据JG/T 128-2017《建筑门窗五金件 撑挡》标准，做如下试验。

图15 关闭方向施加600N/5S

图16 开启方向施加1000N/5S

根据实验数据判定结果为合格。

从试验和理论可以得出在开启距离300mm时，启闭力公式如下：

（启闭力施力位置默认在开启侧距扇型材外缘 50mm处的中点上，未考虑摩擦力）不受风压时：

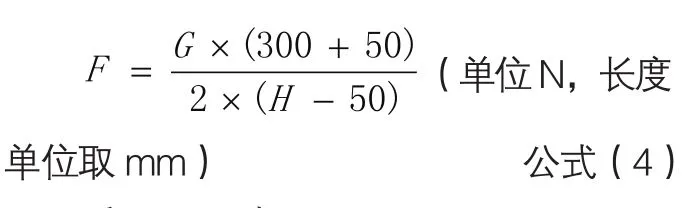
受正风压时：

受负风压时：

注：启闭力F和伸缩撑的轴向受力Q是不一样的。

对以上分析我们做一个小结：

1）无论伸缩撑从框上定位还是从扇上定位，只要离下端距离一样时，伸缩撑本身的轴向的受力是一样的。

2）从公式可知，伸缩撑越靠下面安装，对伸缩撑越有利，伸缩撑轴向受力越小。前提是安装位置要满足伸缩撑的最大展开尺寸与关闭时的最小尺寸。

3）上悬窗重量、尺寸和开启距离一定时，窗扇启闭力与伸缩撑安装位置无关。

这里简单对伸缩撑抗破坏试验的强度做一个演算。

JG/T 128-2017《建筑门窗五金件撑挡》中上悬窗尺寸为1.2m×1.2m，重量为450N；施力点为窗扇开启侧距扇型材外缘 55mm处的中点上，我们选择8寸伸缩撑，尺寸同上。则伸缩撑轴向受力Q在开启和关闭时可分别计算。如：

图17 JG/T 128-2017中试验模拟窗中伸缩撑轴向受力分析图

关闭力为600N：

5秒；伸缩撑受压力；

开启力为1000N：

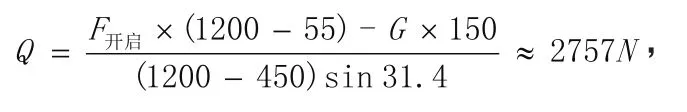
5秒；伸缩撑受拉力。

3.伸缩撑联接点的受力情况分析

对上悬窗的伸缩撑而言，主要是伸缩撑与窗型材之间用自攻螺钉连接的部位受力，导致伸缩撑失效的现象居多。因此下面取伸缩撑与扇联接点，做简要理论分析。

3.1 无风状态下（如图18）

图18 伸缩撑框上定位和扇上定位C联接点受力图

伸缩撑框上定位时，C联接点，从受力分析可知：

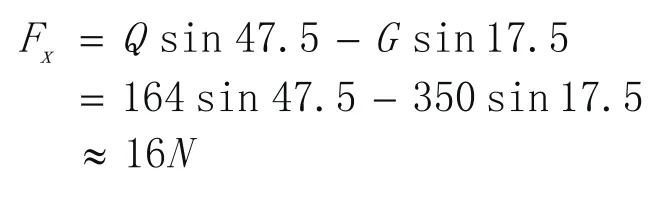
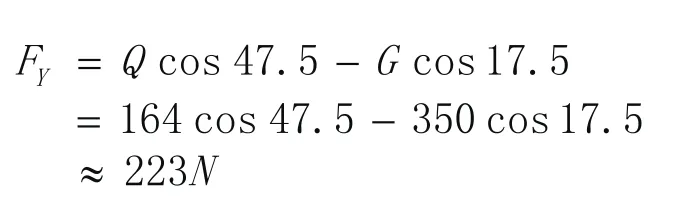
同时虽然受扭矩M=G×0.066=350×0.066=23.1N·m，但因为联接点C是可旋转的轴，所以不考虑扭矩的影响。

伸缩撑扇上定位时，C联接点，从受力分析可知：

从受力情况看，框上定位更有利。

3.2 受正风压（如图19）

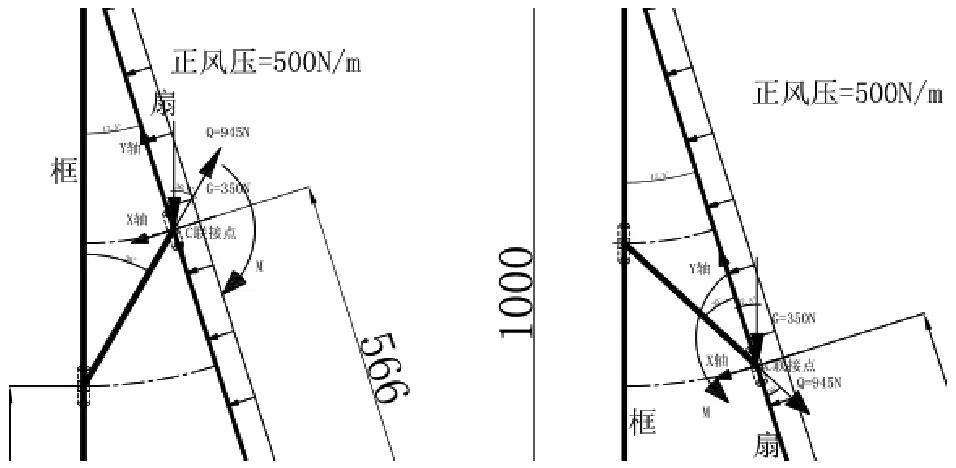
图19 受正风压时，伸缩撑框上定位和扇上定位C联接点受力图

1）受正风压时，伸缩撑框上定位，C联接点，从受力分析可知：

2）受正风压时，伸缩撑扇上定位，C联接点，从受力分析可知：

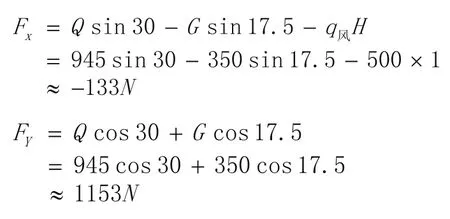
从受力情况看，框上定位更有利。

3.3 受负风压（如图20）

1）受负风压时，伸缩撑框上定位，C联接点，从受力分析可知：

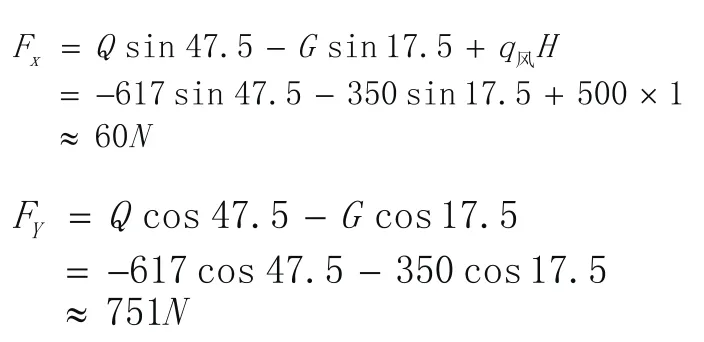
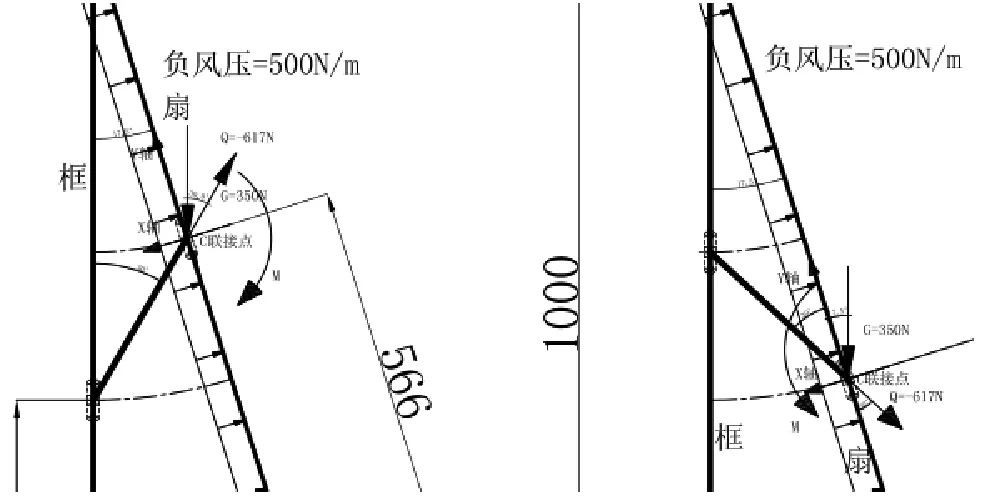
图20 受负风压时，伸缩撑框上定位和扇上定位C联接点受力图

2）受负风压时，伸缩撑扇上定位，C联接点，从受力分析可知：

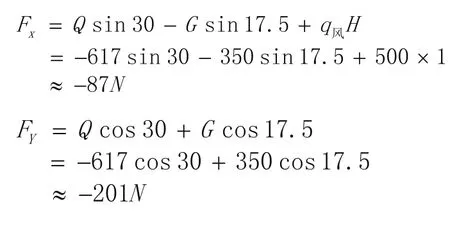
从受力情况看，扇上定位更有利。

以上情况做一个小结：日常不受风压和正风压时，伸缩撑与型材联接点框上定位更有利；如果单独考虑负风压的情况，则扇上定位更有利。

4.在实际工作中的应用

虽然上面我们经过计算，算出开启扇为1m×1m挂勾式上悬窗（采用6+12A+6玻璃，自重定为350N ），使用8寸伸缩撑时的力，但是实际情况下，由于幕墙分格原因，很多幕墙上悬窗都远远超过这个尺寸，2m宽×1.5m高的窗也是很常见的。

我们可以验算如下：

开启扇定为2m宽×1.5m高挂勾式（或合页式）上悬窗，采用6+12A+6玻璃，自重定为1000N ，幕墙开启距离按幕墙规范为300mm，则换算开启角度为11.5°；风荷载标准值取为0.5kPa，其风荷载均布大小为q风=500N/m，垂直于窗扇板，正负风压取值相等。以10寸伸缩撑考虑，开启后伸缩风撑展开长度为360mm，关闭后伸缩撑长度为255mm（展开长度是以中心距计算），经过计算，安装在离下端200mm处，角度为34.7°；只考虑轴拉压且处于开启工作状态。伸缩撑是按一对计算。

根据上面的公式，可以计算得出：

框上定位，受正风压时，上悬窗一对伸缩撑的受力为：

受负风压时，上悬窗一对伸缩撑的受力为：

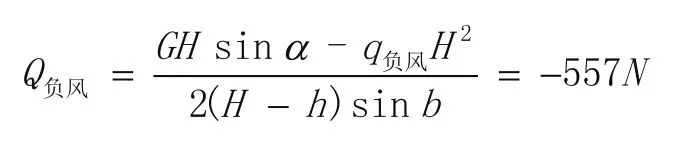
框上定位，联接点C受力，正风压时：

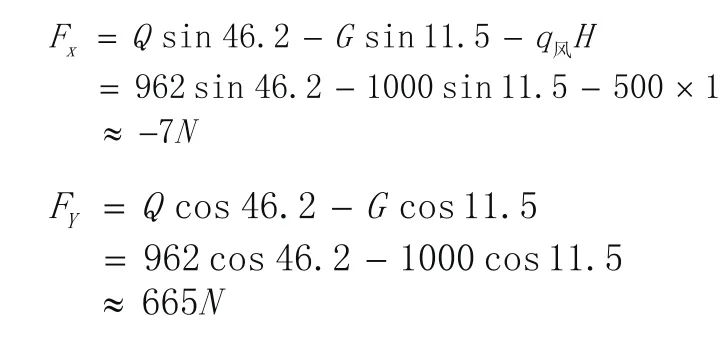
负风压时：

扇上定位， 联接点C受力，正风压时：

负风压时：

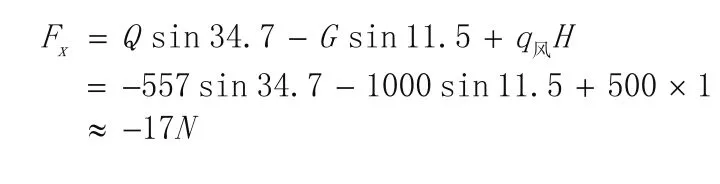
从验算结果来看，联接点C受力在遇到风压时，受力比较大。

目前大部分伸缩撑的联接位置只有两个自攻螺丝位置点，这明显不利。建议增加螺丝孔位，如下图2。

图21 DSFC伸缩撑两端各4个螺丝孔位

实际上很多时候，伸缩撑的损害基本都是集中在几点：两边安装不对称；伸缩撑型号选择错误；受正负风压以及涡流的影响，来回晃动，两边受力不均；以及安装错误的位置无法正常打开，还要强行打开等。

虽然前面我们计算了抗破坏时，伸缩撑的轴向受力，但它是极限荷载情况，只有5秒，数据不能用来做设计荷载用。最少要有两倍的保险系数支撑才可以。

另外安装时，伸缩撑缺口尽可能要冲下，如下图22。

图22 伸缩撑开启关闭示意图

由于伸缩撑是靠里面星形齿轮来定位卡住，星形齿轮自由旋转的惯性动量不是很均匀的情况下，建议缺口方向尽可能与重力方向一致，以便靠重力定位。

5.总结

实践证明，本文理论计算和力学分析得出的结果，符合产品实际情况。

通过以上分析， 得出的结论有以下几点：

5.1 伸缩撑在已知上悬窗尺寸和开启距离的情况下，它的安装位置是有限定的，不是随意安装就可以的。

5.2 伸缩撑的安装无论是框上定位还是扇上定位，伸缩撑轴向受力和启闭力基本上是一样的。考虑风压等因素，一对伸缩撑轴向受力设计荷载建议不要超过1000N。

5.3 在考虑伸缩撑与型材的联接时，应该多点注意联接点的受力情况。日常情况下，正风压时框上定位更有利；如果考虑负风压因素更多时，扇上定位的联接点受力更有利。尽可能采用两端各有4个螺丝孔位的伸缩撑。

我们希望通过本文的分析，给门窗幕墙行业的广大技术爱好者们拓宽思路，为门窗事业的腾飞发展添砖加瓦。