洪水冲刷作用下悬空管道力学响应特性研究*
刘兴华
中海油安全技术服务有限公司湛江分公司
管道是能源的主要输送媒介,截至目前,全球油气管道总里程已超1.96×106km[1]。未来十年内,全球石油天然气资源的管道铺设仍将持续进行,而长输管道的发展伴随着诸多安全问题。例如我国西气东输管线包含尚在规划建设的线路有六条长输管线,管道沿线不可避免地经过河流湖泊等水文地域[2],当河床发生剧烈变化或发生大范围洪水时,管道在水流冲刷作用下会发生弯曲变形,严重的甚至发生折断,从而造成经济损失和环境破坏。
在众多的管道工程中,洪水对管道的影响引发了学者们广泛关注,为管道研究工作做出了贡献。王晓霖等[3]模拟了洪水管道力学研究模型,推算出管道的变形方程解析式。白路遥等[4]基于河床冲刷深度计算的经验公式建立了更实用的河段计算模型。LI Sijia 等[5]利用非线性有限元方法研究漂浮管道的应力应变,基于管土耦合力学模型的基础,建立含缺陷的管道力学模型。詹婷雯[6]基于Morison 方程建立了洪水作用下管道的数值模型,详细分析了管道的应力分布规律。刘旭等[7]利用有限元模拟结果建立洪水灾害下悬空管道的安全评估速查表,提出洪水灾害下的计算流程和安全评估措施。王磊等[8]利用Fluent 软件计算了输气管道外表面的压力分布,继而对整个管道进行受力分析。目前的研究主要集中在管道应力分布方面,但管道的设计多采用应变准则,故同样需要从应变的角度分析管道的失效。本文采用有限元方法建立洪水作用下的管道模型,并讨论了关键参数对管道应力、应变的影响,研究结果可为管道的设计、防护提供有力的支持。
1 洪水作用下的悬空管道模型
在洪水冲刷作用下,浸泡的土体会逐渐变得松软而被冲毁,导致埋地管道产生部分裸露,形成悬空管道,而管道端部仍被掩埋在土体中(图1)。
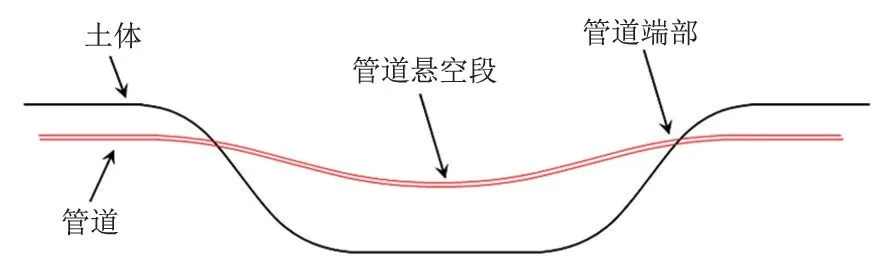
图1 洪水作用下管道示意图Fig.1 Schematic diagram of pipeline under flood action
悬空段的管道受力包括管道自身重力、内部压力、管道两端的管土接触力。此外,洪水的波浪载荷同样会作用在裸露的管道外表面,该波浪载荷从方向上可以分为沿管轴方向的动水作用力、垂直冲刷管道的动水作用力及浮力[9]。
悬空段管道截面受力如图2 所示。依据Morison方程,在洪水作用下,管道单位长度的动水作用力可具体描述为水流横向拖曳力FD、竖向升力FL、惯性力FI[10]。
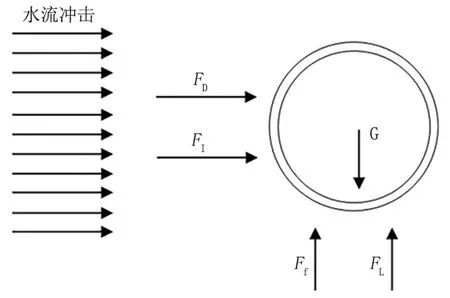
图2 管道截面所受洪水作用力Fig.2 Flood forces on the pipeline section

式中:D为管道外径,m;CD、CL、CM为动水系数;ρw为洪水密度,kg/m3;Ve为平均水流速,m/s;为水平粒子加速度,m/s2。
单位长度管道重力qw的大小主要取决于管材和管内介质,即
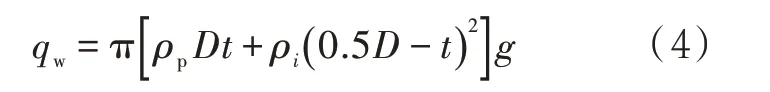
式中:ρp为管材密度,kg/m3;t为管道壁厚,m;ρi为管道内介质密度,kg/m3;g为重力加速度,m/s2。
由阿基米德定理可得,洪水对单位长度管道的浮力Ff为
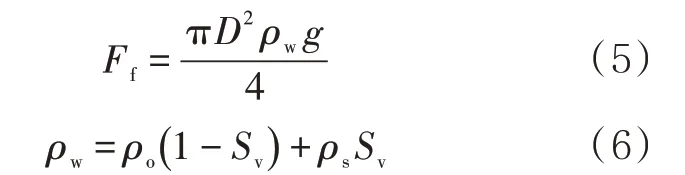
式中:ρo为单位体积洪水和砂的总密度,kg/m3;ρs为单位体积洪水中砂的密度,kg/m3;Sv为体积比砂含量。
其中动水系数与雷诺数的关系如表1[11]所示。

表1 动水系数与雷诺数关系Tab.1 Relationship between hydrodynamic coefficient and Reynolds number
2 数值模型建立
洪水作用在悬空管道的过程中,管道自身重力影响使得其在竖向方向受力变形。洪水载荷作用后,管道外表面会额外受到水平方向和竖向方向的洪水载荷[12]。除此之外,管道内部介质同样会影响管道变形,且管土相互作用对管道端部(管土接触面)的影响较为明显。管道是一种薄壁结构,当管道截面产生大变形时会存在残余应力或应力集中,如果采用传统的解析方法很难准确表达管道的截面变形,因此采用数值模拟方法更适合反映洪水作用下的管道力学响应[13]。
建立图3 所示有限元模型,根据模型载荷和几何结构的对称性,整个模型采用1/2 模型。假设土体形状为立方形,尺寸为12 m×6 m×6 m。油气管道为X65 钢级管道[14],外径为660 mm、壁厚8 mm,屈服强度为448.5 MPa,管道密度r=7 800 kg/m3,泊松比0.3,弹性模量E=210 GPa。管道端部围土采用粉质黏土,本构关系为理想弹塑性Mohr-Coulomb 模型。假设土体具有各向同性。土体的密度值为2 000 kg/m3,弹性模量为12 MPa,泊松比取0.25,黏聚力为50 kPa,膨胀角为22°,内摩擦角为25°[15]。管道外表面与土体采用允许分离的管土接触算法,取管土之间的摩擦系数为0.3[16]。选取洪水速度3 m/s,洪水密度1 120 kg/m3[13],根据Morison理论计算得出水平升力载荷、竖向载升力荷和浮力载荷[17]。
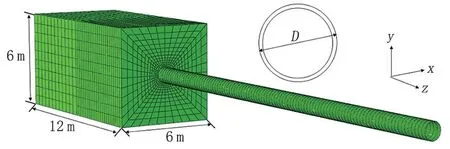
图3 洪水作用下管道有限元模型Fig.3 Finite element model of pipeline under flood action
管道网格的划分类型为四节点壳单元S4R,以C3D8R 八节点减缩积分单元作为土体网格的划分类型,然后着重细化管道附近土体网格[18]。
对整个模型做以下假设:延x轴方向为水平方向,沿z轴方向为管道轴向,沿y轴方向为竖向。对整个模型首先施加初始重力载荷(y轴负方向),而后施加管道内部载荷(作用管道内表面),最后施加洪水载荷(x正方向,y正方向)。土体y-z平面和x-y平面分别采用法向(x方向和z方向)约束,x-z底面采用固定约束,土体顶面为自由面。管道对称面x-y平面采用对称约束[19]。
3 计算结果分析
3.1 悬空长度影响分析
管道悬空后,在自身重力和洪水载荷共同作用下管道受力较为复杂。图4 为洪水作用下不同悬空长度管道应力云图。在重力和洪水载荷作用后,最大位移在悬空管道中部(管道对称面)。当悬空长度为100 m 时,在管道端部(管道出土处)和管道中部(管道对称面)均出现较大的应力集中,但管道端部的应力相对大于管道中部。当悬空长度增大时,管道应力也不断增大,其中,当悬空长度小于60 m时,管道端部的应力小于屈服强度(448.5 MPa)。当悬空长度大于60 m 时,管道端部的应力值大于屈服极限,因此管道发生塑性变形,但此时管道中部应力仍小于屈服强度,且有逐渐稳定的趋势。在管道端部,当悬空长度增大时,管道的高应力区面积沿管道轴向增大,在悬空长度大于90 m 时,其轴向的范围逐渐趋于稳定;此外,高应力区同时也沿管道周向扩展,最终在整个管道周向外表面都呈现较大的应力。在管道端部,虽然管道上表面和下表面均有高应力区,但并不严格位于管道正中间,而是与管道正中平面(y-z平面)存在偏离,并呈中心对称的形式[20]。
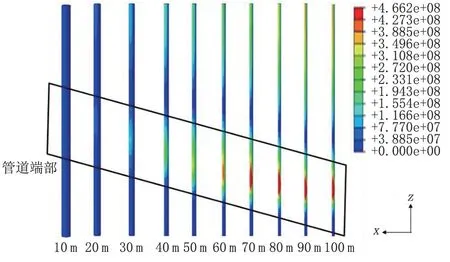
图4 不同悬空长度下管道应力云图Fig.4 Stress cloud picture of pipeline with different suspended length
图5 所示为不同悬空长度下管道最大Mises 应力。当悬空长度小于60 m 时,最大应力的变化率先不断增大后保持稳定。但当悬空长度大于60 m时,管道进入屈服阶段,最大应力开始缓慢增大。
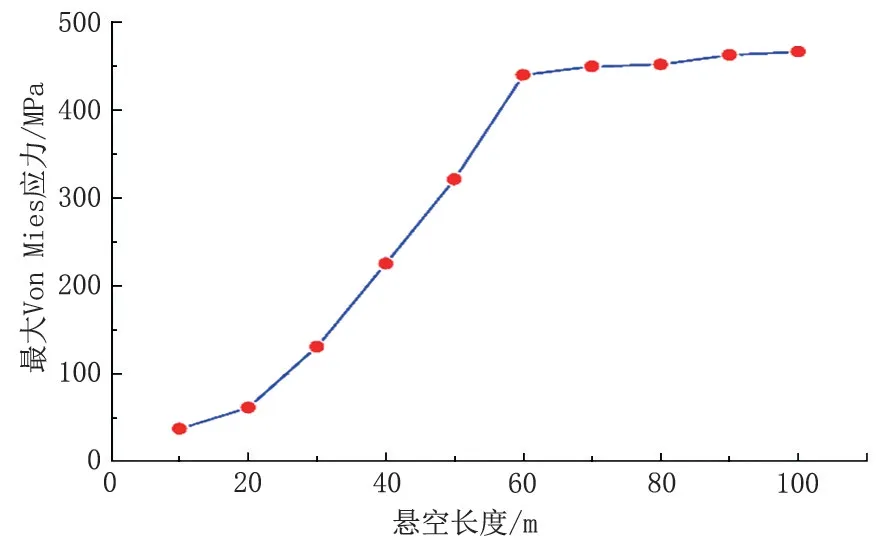
图5 不同悬空长度下管道最大Von Mises 应力Fig.5 Maximum Von Mises stress of pipeline with different suspended length
图6 所示为不同悬空长度下管道上表面和下表面最大轴向应变。管道最大轴向应变对应管道上下表面最大应力,都处于管道端部,管道最大轴向应变与正中对称面存在偏离,但最大应变和最小应变关于管道中心近似呈中心对称。管道上表面受压,为负应变。管道下表面受拉,为正应变。当悬空长度小于60 m 时,管道上下表面最大轴向应变变化量较小,变化率近似呈线性。当悬空长度大于60 m时,管道上下表面最大轴向应变的变化率明显增大。根据CSA 在管道极限状态的设计准则,管道应变极限值大小应为2.5%[21],故当洪水作用下的管道悬空长度大于80 m 时,管道可能失效。
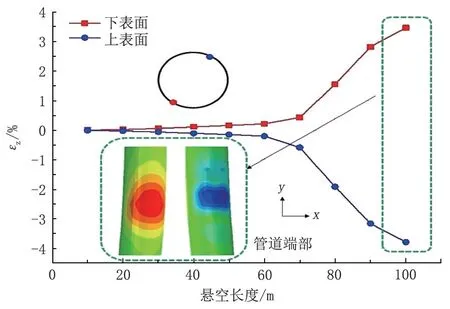
图6 不同悬空长度下管道最大轴向应变Fig.6 Maximum axial strain of pipeline with different suspended length
3.2 洪水流速影响分析
洪水流速会影响管道受到的动水作用力,过大的洪水流速容易造成管道失效。当管道悬空长度为50 m,洪水流速范围为1~5 m/s 时,管道端部和中部应力都随洪水流速增大而不断增大,管道端部和中部高应力区域均延管道轴向扩展,当水流速度大于4 m/s 时,管道端部开始屈服(图7)。整体应力分布与不同悬空长度时较相似。由图8 可知,当洪水速度小于4 m/s 时,最大应力随洪水速度增大明显,增长率不断增大。当悬空长度大于4 m/s 时,最大应力缓慢增大。

图7 不同洪水流速下管道应力云图Fig.7 Stress cloud picture of pipeline under different flood velocity
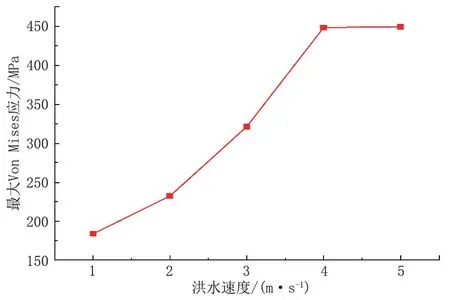
图8 不同洪水流速下管道最大VonMises 应力Fig.8 Maximum Von Mises stress of pipeline under different flood velocity
图9 所示为不同洪水速度下管道上表面和下表面最大轴向应变。管道上、下表面最大应变关于管道中心近似呈中心对称。当洪水速度小于4 m/s时,随着水流速度的增大,管道上、下表面最大轴向应变不断增大,且近似呈线性变化。当洪水速度大于4 m/s 时,增长率较大。
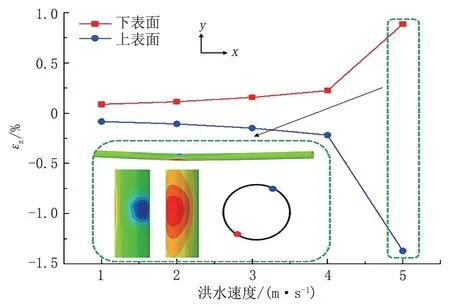
图9 不同洪水速度下管道最大轴向应变Fig.9 Maximum axial strain of pipeline under different flood velocity
3.3 管道壁厚影响分析
管道悬空后在自身重力作用下发生变形,管道悬空段所受重力与管道壁厚成二次函数的非线性关系[12],因此,壁厚对管道的影响与直径是存在差异的,当悬空长度为50 m 时,管道整体应力随管道壁厚增大不断减小,管道端部和中部高应力区变化都比较明显,因为壁厚增大会增大管道刚度,从而降低管道变形(图10)。由图11 可知,管道最大应力随管道壁厚增大不断减小,变化率有减小的趋势,总体变化量比较明显,约225 MPa,且管道始终没有达到屈服强度。
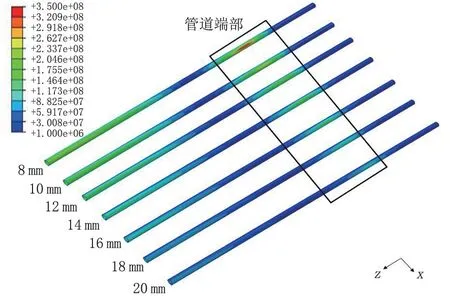
图10 不同管道壁厚下管道应力云图Fig.10 Stress cloud picture of pipeline with different wall thickness
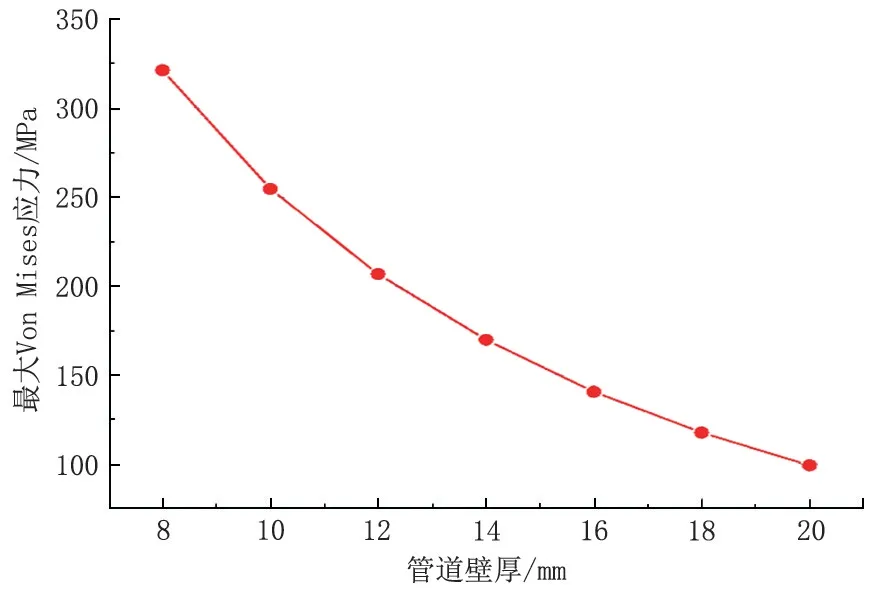
图11 不同壁厚下管道最大VonMises 应力Fig.11 Maximum Von Mises stress of pipeline with different wall thickness
图12 为不同壁厚影响下管道上表面和下表面最大轴向应变。管道上、下表面最大应变随壁厚增大不断减小,且变化率不断减小。

图12 不同壁厚下管道最大轴向应变Fig.12 Maximum axial strain of pipeline with different wall thickness
3.4 管道内压影响分析
当管道壁厚为8 mm,悬空长度为50 m 时,不同压力管道应力如图13 所示。管道内部压力增大会明显提高管道应力,整体应力也会随内压变化而发生改变,管道端部和中部的高应力区都不断增大,并且在高压下管道容易产生屈服。图14 为不同内压影响下管道最大Mises应力。加大管道的内压导致了管道最大应力的增长,变化率不断减小。当内压大于3 MPa 时,最大应力趋于稳定,此时管道已经超过屈服强度,最大应力增长缓慢,但高应力区会不断增大。
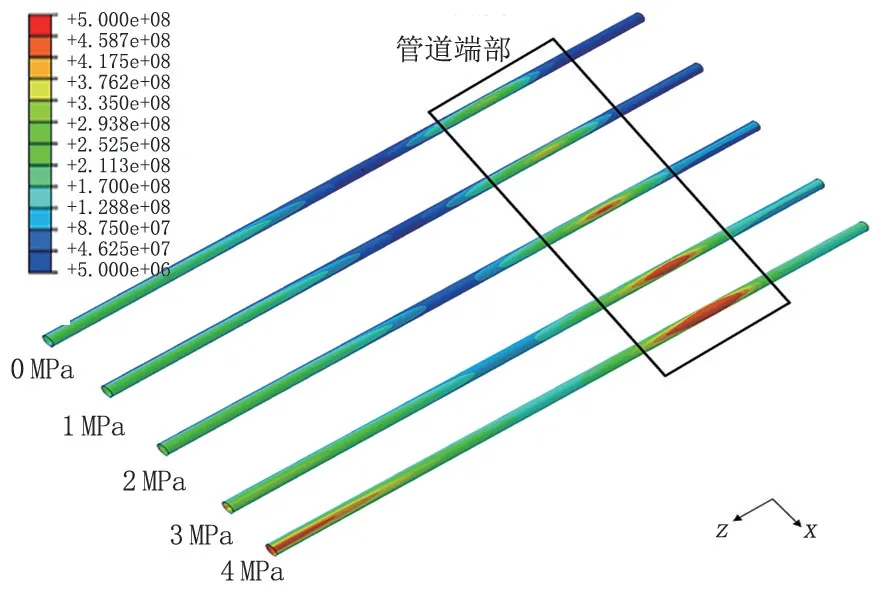
图13 不同内压下管道应力云图Fig.13 Stress cloud picture of pipeline under different internal pressure
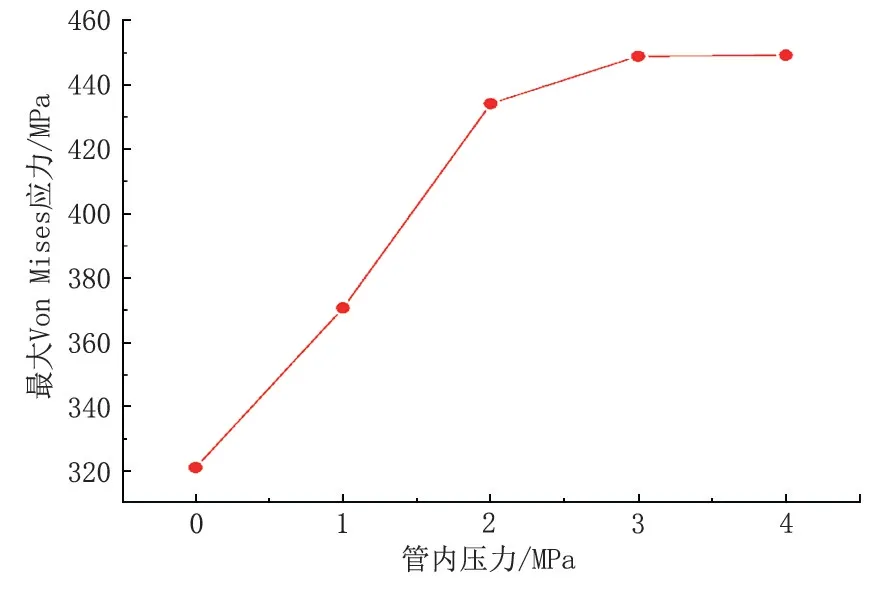
图14 不同内压下管道最大Von Mises 应力Fig.14 Maximum Von Mises stress of pipeline under different internal pressure
图15 为不同内压影响下管道上表面和下表面最大轴向应变。当内压小于3 MPa 时,管道上、下表面最大应变随内压的增大不断增大,变化率近似呈线性。当内压大于3 MPa 时,最大轴向应变增长率增大,轴向应变急剧增大。
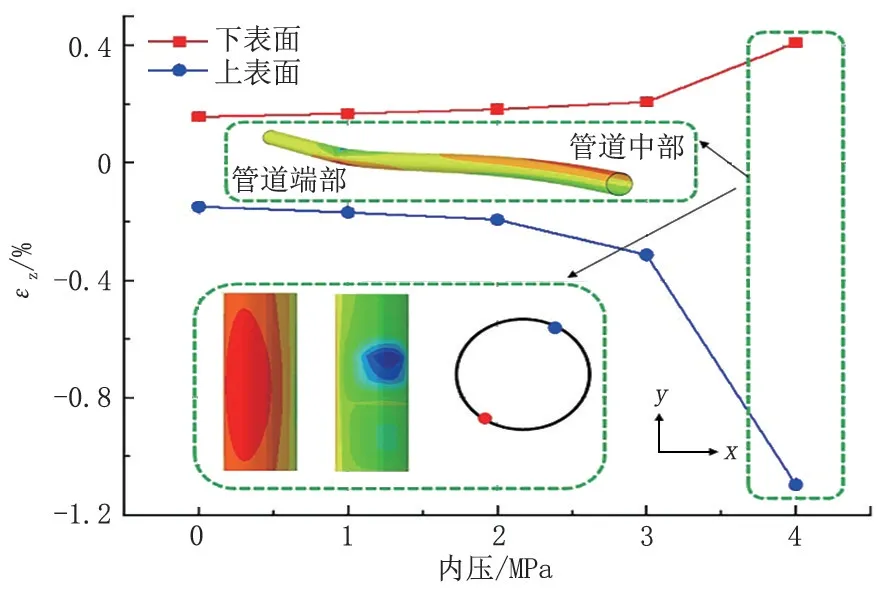
图15 不同内压下管道最大轴向应变Fig.15 Maximum axial strain of pipeline under different internal pressure
4 结论
(1)采用有限元法建立了洪水载荷下悬空管道数值模型,研究了悬空管道的变形规律。发现随着管道悬空长度的增大,管道应力、应变都增大。悬空管道中部和端部均存在高应力区,但最大应力在管道端部,当悬空长度大于60 m 管端部容易产生屈服。管道上、下表面最大轴向应变都位于管道端部,最大应变和最小应变关于管道中心近似呈中心对称。管道上表面为压应变,下表面为拉应变。
(2)管道应力和轴向应变随洪水速度和管道内部压力增大而增大,当悬空长度为50 m,洪水流速大于3 m/s 或管道内压大于3 MPa 时,管道容易屈服。管道应力、应变随管道壁厚增大而减小,且当悬空长度为50 m 时,不同壁厚的管道均未产生屈服。

