坡体及其支护结构稳定性验算强制性规定的分析

方玉树

（1 陆军勤务学院，重庆 401311； 2 岩土力学与地质环境保护重庆市重点实验室，重庆 401311）

0 引言

全文强制的《建筑和市政地基基础通用规范》（GB 55003—2021）（以下称《地基通用规范》）对坡体及其支护结构稳定性验算作出了规定。 具体情况是：

第7.2.3 条由两款构成，其第1 款规定：“支护结构稳定性验算应符合下式规定：

式中：Rk——抗滑力、抗滑力矩、抗倾覆力矩、锚杆和土钉的极限抗拔承载力等土的抗力标准值；Sk——滑动力、滑动力矩、倾覆力矩、锚杆和土钉拉力等作用标准值的效应；K——安全系数。 ”

第7.2.3 条第2 款规定：“悬臂式和单支点支护结构应验算抗倾覆、整体稳定及结构抗滑移稳定性；多支点支护结构应验算整体稳定性。 ”

第2.2.2 条第3 款规定：“计算挡土墙、地基或滑坡稳定……时，作用效应应按承载能力极限状态下作用的基本组合，但其分项系数均为1.0。 ”

第7.2.3 条规定来自“基坑工程”一章，是针对基坑工程的，“边坡工程”一章第8.1.2 条有“边坡工程设计应根据不同的工况进行整体稳定性分析与验算”的规定，第8.2.1 条有“支挡结构设计计算或验算应包括……支挡结构稳定性验算”的规定，但该章没有与第7.2.3 条第1 款对应的规定。 根据“边坡工程”一章位于“基坑工程”一章之后这个排序和基坑工程与边坡工程的相似性， 可以认为边坡工程稳定性验算要求与该规定相同。 如果不能这样认识，则意味着《地基通用规范》在边坡工程稳定性验算要求方面未作规定，存在边坡工程稳定性验算要求的缺项，此时，如果在边坡工程稳定性验算方面采用与第7.2.3 条相同的做法，那是符合《地基通用规范》精神的。

本文对这些规定进行讨论并提出建议，关于《地基通用规范》第7.2.3 条第1 款在锚杆和土钉抗拔承载力验算方面存在的问题和处理建议，笔者已另文论述[1]。

1 关于坡体抗滑稳定性验算

关于坡体稳定性验算，《地基通用规范》第7.2.3 条第1 款存在缺项。

坡体治理不仅仅是支护，还包括放坡。 设计坡形下坡体是否需要进行抗滑治理需要通过设计坡形下的稳定性验算来确定， 岩质坡体和高度不大且粘聚力不很低的土质坡体尤其如此。 因此，规范中的边坡工程和基坑工程章节包含坡体稳定性验算内容是理所当然的。 从所用“抗滑力、抗滑力矩……等土的抗力”和“滑动力、滑动力矩”词句来看，该款似乎已包含或可以包含土质坡体抗滑稳定性验算。 但是，该款开头便将稳定性验算限定为支护结构稳定性验算， 而坡体抗滑稳定性验算与支护结构稳定性验算是两回事，因此，该款不包含无支护或支护前的坡体抗滑稳定性验算。 《地基通用规范》 其他条款也未在坡体抗滑稳定性验算方面提出作用组合选择要求和性质同（7.2.3）式的坡体抗滑稳定性满足要求的判断标准。

该规范“基坑工程”一章及其他章节甚至未要求进行基坑边坡稳定性验算。

这些都表明该规范在坡体抗滑稳定性验算方面存在缺项。

根据上述分析，笔者主张：

（1） 要求对基坑工程进行基坑边坡抗滑稳定性验算；

（2） 提出坡体抗滑稳定性验算作用组合选择的要求和性质同（7.2.3）式的坡体抗滑稳定性满足要求的判断标准。

2 关于坡体支护结构地基稳定性验算

关于支护结构地基稳定性验算，《地基通用规范》 第7.2.3 条存在两类问题。

2.1 用语方面

（1） 第2 款采用“支护结构整体稳定性”的称谓不妥。 支护结构整体是与支护结构局部相对的，它就是支护结构外表面所包围的部分。 简单地说，“支护结构整体”说的仍是支护结构而不包含其他。 对于水泥土重力式挡墙，支护结构整体就是墙顶、墙底、墙面和墙背所包围的部分——墙体，支护结构整体稳定性验算就是挡墙抗倾覆和抗滑移稳定性验算。《地基通用规范》第7.2.3 条第2款对悬臂式和单支点支护结构要求在抗倾覆和抗滑移稳定性验算之外进行支护结构整体稳定性验算，意味着：对于水泥土重力式挡墙，该款中的支护结构整体稳定性并非指挡墙抗倾覆和抗滑移稳定性，而是指潜在滑面位于土体内的挡墙与土体组合体稳定性。既然如此，这种稳定性就不应称作支护结构整体稳定性。不难看出，这种稳定性实际上是支护结构地基稳定性，只不过这里的地基表面不是平坦的，在整个支护结构的后侧也有地表高程一般不小于支护结构顶面高程的岩土体，整体上是坡状地形。 支护结构地基稳定性在性质上与坡体稳定性同属于岩土体稳定性，也是尺度有所扩大的坡体稳定性。

（2） 第1 款“抗滑力、抗滑力矩……等土的抗力”提法不妥。第7.2.3 条中的“支护结构”不排除岩质坡体支护结构，“抗滑力”和“抗滑力矩”不排除岩质坡体抗滑力和抗滑力矩，同时《地基通用规范》很多条款有“岩土”的提法，个别条款有“嵌岩桩”的提法，故在该规范中“土”不代表“岩土”。 但该条第1 款采用“抗滑力、抗滑力矩……等土的抗力”提法，却导致不应被排除的坡体支护结构岩质地基稳定性验算被排除在外。

2.2 稳定性验算要求方面

（1） 对考虑条间力的非直线形滑动，因不引入抗滑稳定系数概念、不给出不同于抗滑力（力矩）与滑动力（力矩）之比的抗滑稳定系数定义，抗滑力（力矩）与滑动力（力矩）之比无法求出。

对于坡体滑动，公式（7.2.3）的要求就是抗滑力（力矩）与滑动力（力矩）之比不小于安全系数。 当考虑条间力时，要求出抗滑力（力矩）与滑动力（力矩）之比需要建立各条块力平衡方程，但不引入抗滑稳定系数概念、不给出不同于抗滑力（力矩）与滑动力（力矩）之比的抗滑稳定系数定义，各条块力平衡方程便不能建立。

例如：对圆弧形滑面，当假定条间力方向水平时，要求出抗滑力矩与滑动力矩之比，需要建立各条块竖向力平衡方程，这就需要引入抗滑稳定系数概念、给出不同于抗滑力矩与滑动力矩之比的抗滑稳定系数定义。 若将抗滑稳定系数定义为滑面抗剪强度与剪应力之比（即滑面强度参数调整系数），便获得简化毕肖普法。

再如：对折线形滑面，当假定条间力方向与上一条块滑面平行时，要求出最末条块累积抗滑力与累积滑动力之比，需要建立各条块滑面切向力和法向力平衡方程，这就需要引入抗滑稳定系数概念、给出不同于最末条块累积抗滑力与累积滑动力之比的抗滑稳定系数定义。 若将抗滑稳定系数定义为滑面抗剪强度与剪应力之比（即滑面强度参数调整系数），便获得剩余滑动力法之抗滑力调整法。 若将抗滑稳定系数定义为滑动力调整系数，便获得剩余滑动力法之滑动力调整法，但这种方法不满足力的分解和合成原理继而不满足力平衡，应予放弃。 正因为不关注稳定系数定义才让不满足力平衡的滑动力调整法作为坡体稳定性计算方法在我国广泛应用了近40 年， 作为坡体支护结构岩土荷载计算方法在我国广泛应用了约50 年，该法至今仍在一些标准中存在。

要在不引入抗滑稳定系数概念、不给出不同于抗滑力（力矩）与滑动力（力矩）之比的抗滑稳定系数定义之条件下，求得抗滑力（力矩）与滑动力（力矩）之比，只得不考虑事实上存在的条间力，即：对圆弧形滑面采用瑞典法，对既非圆弧形也非直线形滑面采用投影和法（此法无名称，系笔者为叙述方便暂用之名，在该法中，抗滑稳定系数取不考虑条间力时的各条块抗滑力投影和与滑动力投影和之比）。 瑞典法是世界上最早的用于圆弧形滑面的条分法， 投影和法是1970 年代以前在我国滑坡治理工程中曾用过的条分法[2]。 因没有考虑事实上存在的条间力（后者还因抗滑力与滑动力之比无明显物理意义且无确定值，见下面的几点分析），前者已逐渐淘汰（房屋建筑和市政工程边坡稳定性验算用简化毕肖普法取代该法已有8 年之久），后者已淘汰四十多年（因使用年代久远，很多人不知晓我国曾使用过这种方法，笔者也是在查阅文献后才获知）。 虽然葛修润先生在本世纪初由此发展出主要用于数值分析的矢量和法[3]，但未考虑事实上存在的条间力这个缺陷依然存在[4]。

（2） 对不考虑条间力的非直线形滑动，抗滑力与滑动力之比无明确的物理意义。 对这种滑动，因各条块的抗滑力之间或滑动力之间方向不同，总的抗滑力或总的滑动力只能取投影和或矢量和，但各条块的滑动方向是沿各自底面而不是统一沿投影面或矢量和方向滑动。 因此，这种投影和或矢量和是没有明确的物理意义的， 相应投影和之比或矢量和之比也是没有明确的物理意义的。

（3） 对直线形滑动，因不明确抗滑力构成，抗滑力与滑动力之比无确定值。

一个力平行滑面的分力对抗滑有利时， 既可视为抗滑力，又可视为负的滑动力； 一个力平行挡墙底面的分力对抗滑不利时，既可视为滑动力，又可视为负的抗滑力。 这将导致抗滑力与滑动力之比对不同的抗滑力构成有不同的值。

举一个简单的例子：一个斜面上置有一个块体，仅受重力作用时它有一个确定的稳定状态；当平行滑动方向对块体施加一对相反的推力时，稳定性应无变化。 但在计算抗滑力与滑动力之比时，若不明确抗滑力构成，那么这个比值是不确定的：将这对相反的推力均视为滑动力时，这个比值不变；将顺滑向的推力视为滑动力而将逆滑向的推力视为抗滑力时，这个比值是另外一个值。

从力学上说，任何一个力均可视为两个作用点相同而方向相反的力的代数和。 当将滑动力视为绝对值大的正值力与绝对值小的负值力的代数和时，若将两力均视为滑动力，则抗滑力与滑动力之比不变；若将绝对值大的正值力视为滑动力、将绝对值小的负值力视为抗滑力，抗滑力与滑动力之比将有不同值。 因代数和不变的两力有无数个，后一种处理将使抗滑力与滑动力之比有无数个值。

也许有人认为： 坡体抗滑稳定性验算不用考虑得那么复杂，作用在单个滑块上的力（包括分力）大小和方向是明确的，它们中哪些力对抗滑有利，哪些力对抗滑不利也是明确的。 将各个平行滑面的对抗滑有利和不利的力分别求和， 便可得抗滑力和滑动力，从而可得抗滑力与滑动力之比。

但是，这样做会导致力的分解和合成原理得不到遵守。

例如：对于坝基岩体沿倾向上游的结构面滑动，设坝体迎水面直立，记抗滑力与滑动力之比为Fs，当把由坝体和坝基岩体组成的潜在滑体重力平行反倾滑面的分力视为抗滑力时，不计坝体背水面水压力和岩体结构面水压力条件下的Fs计算式为：

式中：W——由坝体和坝基岩体组成的潜在滑体重力；V——坝体迎水面水压力；α——反倾滑面倾角；L——反倾滑面长度；c——滑面粘聚力；f——滑面摩擦系数。

该式可写成下列二式：

因（2）式中同时出现FsVcosα 和Vsinα，两者合力既不是V也不是FsV，（3）式中同时出现Vsinα 和Vcosα，两者合力既不是V也不是，故（2）式和（3）式不满足力的分解和合成原理，因而，（1）式不满足力的分解和合成原理。 而不满足力的分解和合成原理就意味着不满足力平衡。

况且，在不明确抗滑力构成的情况下，人们完全可以甚至更愿意采取另一种做法： 先计算某些对抗滑有利和不利力的差值，再根据差值的正负确定是对抗滑有利或不利的力。 例如：当潜在滑面上存在水压力时，该水压力减小了潜在滑面正压力使得摩擦力降低，因而对抗滑不利，但人们一般不是将该水压力引起的负摩擦力视为滑动力，而是将其视为负值抗滑力。 这必然造成抗滑力与滑动力之比有不同的值。

抗滑力与滑动力之比无确定值的后果是，对于确定的稳定安全系数，抗滑稳定性是否满足要求将是各说各话，这就造成执行和监督执行（判断是否违反强制性条文）的困难和混乱。

（4） 对非直线形滑动，无论是否考虑条间力，因不明确抗滑力构成，抗滑力与滑动力之比无确定值。 1970 年代以前和以后我国先后用过的投影和法（不考虑条间力）和剩余滑动力法（考虑条间力）之滑动力调整法对滑面反倾条块滑动力就曾有过视为抗滑力和视为负值滑动力两种处理方式。

笔者的研究表明，对坡体滑动，无论是采用条分法是采用数值分析法，抗剪强度参数调整系数是唯一通用的抗滑稳定系数定义，它是这样的系数：滑面粘聚力和内摩擦系数这两个抗剪强度参数按除以该系数的方式调整后， 坡体刚好处于极限平衡状态。滑面抗剪强度与剪应力之比（即毕肖普等人定义）就是抗剪强度参数调整系数。

就直线形滑动而言，为使抗滑力与滑动力之比在确定的力系中有确定值， 需要明确抗滑力仅仅由摩擦力项和粘聚力项构成。在此情况下， 不属于摩擦力项和粘聚力项的各种力都归入滑动力。 因抗滑力与滑动力有相同的作用面积（即滑面面积），所以，对直线形滑动而言，滑面抗剪强度与剪应力之比就是抗滑力仅仅由摩擦力项和粘聚力项构成时的抗滑力与滑动力之比。

对各种滑面形态的滑动，滑面抗剪强度与剪应力之比都是单位面积抗滑力仅仅由摩擦力项和粘聚力项构成时的单位面积抗滑力与滑动力之比。 因此，如果想将抗滑稳定系数定义表达为某种形式的抗滑力与滑动力之比，或者想了解抗滑稳定系数定义同抗滑力与滑动力之比的关系，那么，抗滑稳定系数就是单位面积抗滑力仅仅由摩擦力项和粘聚力项构成时的单位面积抗滑力与滑动力之比。

关于坡体抗滑稳定系数定义，拙著[4]有专章论述。

为此，笔者主张：

（1） 将支护结构整体稳定性改称为支护结构地基稳定性；

（2） 引入抗滑稳定系数概念；要求抗滑稳定系数不小于抗滑稳定安全系数； 将抗滑稳定系数定义为抗剪强度参数调整系数，即滑面抗剪强度与剪应力之比。

其中，第二点主张对常规坡体稳定性验算同样适用。

3 关于挡墙抗滑移和抗倾覆稳定性验算

关于挡墙抗滑移和抗倾覆稳定性验算，《地基通用规范》第7.2.3 条第1 款和第2 款存在两类问题。

3.1 归类和用语方面

（1） 第1 款将挡墙抗倾覆力矩归为土的抗力是错误的。 挡墙自重引起的抗倾覆力矩不属于土的抗力。

（2） 将挡墙抗倾覆和抗滑移稳定性验算扩展为支护结构抗倾覆和抗滑移稳定性验算不妥。 挡墙类型很多，除了重力式挡墙，还有悬臂式挡墙、扶壁式挡墙、加筋土挡墙以及锚拉桩挡墙中的排桩部分、锚杆挡墙中的肋柱部分等等。对单支点支护结构进行抗倾覆和抗滑移稳定性验算，实际上是对其中的墙式部分（桩）进行抗倾覆和抗滑移稳定性验算， 在计算中作为支护结构组成部分的锚杆只视作一个后拉力，锚杆重力及其作用点并没有也不应参与计算。对单支点支护结构而言， 进行支护结构抗倾覆和抗滑移稳定性验算将使验算无法进行。因此，不应将挡墙抗倾覆和抗滑移稳定性验算扩展为支护结构抗倾覆和抗滑移稳定性验算。

（3） 第1 款“抗滑力……等土的抗力”提法不妥。 第7.2.3 条中的“支护结构”不排除岩质坡体支护结构，“抗滑力”不排除岩质坡体抗滑力，同时《地基通用规范》很多条款有“岩土”的提法，个别条款有“嵌岩桩”的提法，故在该规范中“土”不代表“岩土”。 但该条第1 款采用“抗滑力……等土的抗力”提法，却导致不应被排除的岩质地基上挡墙抗滑稳定性验算被排除在外。

3.2 验算要求方面

（1） 因不明确抗滑力构成，挡墙抗滑移稳定性验算中的抗滑力与滑动力之比无确定值。

挡墙沿基底的滑移属于直线形滑动。 在挡墙抗滑移稳定性验算中，潜在滑体为挡墙，潜在滑面为挡墙下端与岩土体接触面而非岩土体内的结构面，潜在滑面强度为岩土体的外强度（与其他物体的接触强度）而非岩土体的内强度，如同背后填方的重力式挡墙之墙背摩擦角为土的外摩擦角而非土的内摩擦角。

挡墙抗滑移稳定性验算中的抗滑力与滑动力之比在抗滑力构成不明确时无确定值的道理与坡体抗滑稳定性验算相同，详见上节所述。

当前，在进行挡墙抗滑移稳定性验算时，相关规范，如《建筑边坡工程技术规范》（GB 50330—2013）和《建筑地基基础设计规范》（GB 50007—2011）， 是将挡墙重力平行逆坡基底的分力视为负值滑动力的。 但如果不明确抗滑力的构成，也可以甚至更愿意将此分力视为抗滑力，做如此变化后，抗滑力与滑动力之比将发生变化。 设墙背岩土荷载方向水平，记抗滑力与滑动力之比为Fs，当把挡墙重力平行逆坡基底的分力视为抗滑力时，不计墙前反压和墙底水压条件下的Fs计算式将与（1）式相同（式中W相当于挡墙重力，V相当于墙背岩土荷载，α 相当于逆坡基底倾角，L相当于逆坡基底长度），相应Fs表达式不满足力的分解和合成原理，继而不满足力平衡。

对挡墙沿基底的滑动，与坡体滑动同理，抗剪强度参数调整系数是唯一通用的抗滑稳定系数定义。 这意味着抗滑力仅仅由摩擦力项和粘聚力项构成。 因此，对挡墙沿基底滑动这种直线形滑动，滑面抗剪强度与剪应力之比就是抗滑力仅仅由摩擦力项和粘聚力项构成时的抗滑力与滑动力之比。

（2） 因不明确抗倾覆力矩构成，挡墙抗倾覆稳定性验算中的抗倾覆力矩与倾覆力矩之比无确定值。

一个力矩对抗倾覆有利时，既可视为抗倾覆力矩，又可视为负的倾覆力矩；一个力矩对抗倾覆不利时，既可视为倾覆力矩，又可视为负的抗倾覆力矩。 这将导致抗倾覆力矩与倾覆力矩之比对不同的抗倾覆力矩构成有不同的值。

关于这一点，墙前、墙底和墙背有水压力时，水泥土挡墙抗倾覆稳定性验算是一个典型的例子。 验算中，墙面水压力和墙底水压力的定位有4 种组合供选择，即：①墙面水压力视为抗力，墙底水压力视为作用；②墙面水压力视为抗力，墙底水压力视为负的抗力；③墙面水压力视为负的作用，墙底水压力视为负的抗力；④墙面水压力视为负的作用， 墙底水压力视为作用。 分别采用这4种组合时，抗倾覆力矩与倾覆力矩之比将有4 个不同值。 这4 种组合中，只有第4 种才符合“接触面性质不随方向变化时接触面一点的水压不随方向变化”这一基本规律，而这一规律是涉及水力时力平衡的基础， 不遵守这一基本规律就意味着不满足力平衡。由于忽视了这一基本规律，先后实施过的全部（3 部）基坑工程行业标准，即《建筑基坑工程技术规范》（YB 9258—97）、《建筑基坑支护技术规程》（JGJ 120—99）和《建筑基坑支护技术规程（JGJ 120—2012）》，选择了所有（3 种）不正确的组合而恰恰放过了那一个正确的组合。

从力学上说，任何一个力矩均可视为两个旋转中心相同而方向相反的力矩的代数和。 当将倾覆力矩视为绝对值大的正值力矩与绝对值小的负值力矩的代数和时， 若将两力矩均视为倾覆力矩，则抗倾覆力矩与倾覆力矩之比不变；若将绝对值大的正值力矩视为倾覆力矩、将绝对值小的负值力矩视为抗倾覆力矩，抗倾覆力矩与倾覆力矩之比将有不同值。 因代数和不变的两力有无数个，后一种处理将使抗倾覆力矩与倾覆力矩之比有无数个值。

也许有人认为： 挡墙抗倾覆稳定性验算不用考虑得那么复杂，只要作用在挡墙上的力（包括分力）大小、方向和作用点是明确的，它们中哪些力引起的力矩对抗倾覆有利，哪些力引起的力矩对抗倾覆不利就是明确的。 将各个对抗倾覆有利和不利的力矩分别求和，便可得抗倾覆力矩和倾覆力矩，从而可得抗倾覆力矩与倾覆力矩之比。

但是，这样做会导致力的分解和合成原理及“接触面性质不随方向变化时接触面一点的水压不随方向变化”的规律得不到遵守。

例如：当前，在进行重力式挡墙抗倾覆稳定性验算时，相关规范，如《建筑边坡工程技术规范》（GB 50330—2013）和《建筑地基基础设计规范》（GB 50007—2011），是将墙背岩土荷载竖直分力引起的力矩视为抗倾覆力矩的。 此时，如果记抗倾覆力矩与倾覆力矩之比为Ft，那么不计墙前反压和墙底水压条件下Ft的计算式为：

式中：G——挡墙每延米自重（kN/m）；Tzk、Txk——墙背每延米岩土荷载Tk的竖直分力、水平分力（kN/m）；x0——挡墙中心到墙趾的水平距离（m）；xf、zf——墙背每延米岩土荷载竖直分力、水平分力的力臂（m）。

上式可写成下列二式：

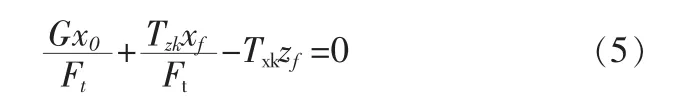
或

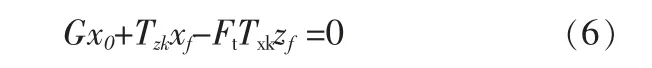
因（5）式中同时出现Tzk/Ft和Txk，两者合力既不是Tk又不是Tk/Ft，（6） 式中同时出现Tzk和FtTxk， 两者合力既不是Tk又不是FtTk，故（5）式和（6）式不满足力的分解和合成原理，因而，（4）式不满足力的分解和合成原理。 而不满足力的分解和合成原理就意味着不满足力矩平衡。

况且，在不明确抗倾覆力矩构成的情况下，人们完全可以采取另一种做法： 先计算某些对抗倾覆有利和不利力矩的差值，再根据差值的正负确定是对抗倾覆有利或不利的力矩。 这必然造成抗倾覆力矩与倾覆力矩之比有不同的值。

为满足力平衡，需要将抗倾覆力矩明确为含有抗力参数的抗力项。 抗力参数的特点是：它是稳定性验算对象——潜在运动体自身或与周围物体接触面的性质指标不是力和尺寸，且仅在抗力项中出现。 对挡墙倾覆而言，挡墙重力引起的力矩是抗力项，它含有抗力参数——挡墙重度， 挡墙重度是抗倾覆稳定性验算对象——挡墙自身的物理性质指标不是力和尺寸，且仅在抗倾覆力矩中出现。 若引入抗倾覆稳定系数概念，那么，抗倾覆稳定系数应定义为挡墙重度调整系数，它是这样的系数：挡墙重度这个抗力参数按除以该系数的方式调整后， 挡墙刚好处于极限平衡状态。这意味着抗倾覆力矩只能是挡墙重力引起的力矩。

根据上述可知，引入抗倾覆稳定系数概念对抗倾覆稳定性验算议题的分析要方便得多。

关于挡墙抗倾覆稳定系数定义，笔者另文有专门研究[5]，拙著[4]也有较多论述。

（3） 墙背岩土荷载未区别对待。 笔者的研究表明，坡体支护结构岩土荷载需分为抗失稳支护结构岩土荷载和抗变形支护结构岩土荷载，抗失稳支护结构岩土荷载需采用按稳定性公式反算法计算，其结果与稳定安全系数有关，随其增大而增大[4]。 因此，抗失稳挡墙抗倾覆和抗滑移稳定安全系数取值需小于抗变形挡墙抗倾覆和抗滑移稳定安全系数，如同抗失稳支护结构中单桩水平承载安全系数取值需小于抗变形支护结构中单桩水平承载安全系数，抗失稳支护结构中锚杆承载安全系数取值需小于抗变形支护结构中锚杆承载安全系数[1，4]。

根据上述分析，关于挡墙抗滑移和抗倾覆稳定性验算，笔者主张：

（1） 不将挡墙抗倾覆力矩归为土的抗力，将支护结构抗倾覆和抗滑移稳定性改称为挡墙抗倾覆和抗滑移稳定性；

（2） 分别引入挡墙抗滑移和抗倾覆稳定系数概念；要求挡墙抗滑移和抗倾覆稳定系数分别不小于挡墙抗滑移和抗倾覆稳定安全系数；将挡墙抗滑移和抗倾覆稳定系数分别定义为墙底抗剪强度参数调整系数和挡墙重度调整系数；抗失稳挡墙抗倾覆和抗滑移稳定安全系数取值小于抗变形挡墙抗倾覆和抗滑移稳定安全系数。

应当指出，对于岩土体抗滑稳定性验算、挡墙抗滑移和抗倾覆稳定性验算以及其他稳定性验算，给出稳定系数定义与安全系数法中安全系数是综合考虑各种因素误差的结果， 是不矛盾的，因为无论安全系数是什么，稳定系数计算作为力学计算都必须满足三个条件：一是力平衡，二是对确定的力系有确定的稳定系数，三是同类型稳定系数计算结果之间可以比较，即抗滑稳定系数计算结果之间可以比较， 抗倾覆稳定系数计算结果之间可以比较。否则稳定系数计算没有意义。 因此，给出稳定系数定义是必须的。

4 关于坡体及其支护结构稳定性验算的几个共性问题

4.1 所用荷载是分项系数为1.0 的作用标准值还是作用设计值

关于坡体及其支护结构稳定性验算所用荷载是分项系数为1.0 的作用标准值还是作用设计值，《地基通用规范》第2.2.2 条第3 款与第7.2.3 条第1 款是矛盾的，第2.2.2 条第3 款要求是前者，第7.2.3 条第1 款要求是后者。 规定的矛盾将造成执行和监督执行的混乱。

是统一采用第2.2.2 条第3 款的规定还是统一采用第7.2.3条第1 款的规定呢？ 地基承载力验算和坡体、支护结构地基、挡墙抗滑移稳定性验算都属于岩土体强度验算，当地基承载力验算采用安全系数法时，可以获得与边坡地基承载力验算等效的边坡地基稳定性验算方法，不考虑埋深影响的挡墙抗滑移稳定性验算就是挡墙底面抗剪承载力验算， 它类似于抗拔桩抗拔承载力验算，只是受剪方向由竖直变成水平、受剪面由封闭的柱面变成一个平面。 因此，坡体及其支护结构稳定性验算中的作用效应表述应与地基承载力验算中的相同。

为此，笔者主张，《地基通用规范》第2.2.2 条第3 款中的作用效应表述改为与第7.2.3 条第1 款中的相同， 即采用作用标准值的提法。

需要说明的是，与完全由岩土体构成的坡体抗滑稳定性验算和把支护结构视为土体一部分的支护结构地基抗滑稳定性验算不同，有支护坡体抗滑稳定性验算需考虑支护结构承担岩土荷载的能力——支护力。 在坡体抗滑稳定性验算中，抗滑稳定系数是滑面强度参数调整系数（即滑面抗剪强度与剪应力之比），故支护力是视为对坡体抗滑有利的作用（荷载）的。 但这个荷载情况特殊，它不是支护结构承担坡体所传岩土荷载的极限能力，而是在满足安全度要求的条件下支护结构承担坡体所传岩土荷载的最大能力，这个安全度要求对分项系数法而言，就是考虑抗力分项系数、荷载分项系数（对抗失稳支护结构取1）和支护结构重要性系数（对抗失稳和抗变形支护结构均取1），对安全系数法而言，就是考虑承载或稳定安全系数（抗失稳支护结构安全系数取值小于抗变形支护结构安全系数取值）[1]。 支护力与在满足安全度要求的条件下支护结构所能承担的最大岩土荷载大小相等、方向相反并在同一条作用线上。 这样的支护力在有支护坡体稳定性验算中只是视为作用标准值，并非真正的作用标准值。

4.2 是否考虑地震工况

根据《地基通用规范》第7.2.3 条第1 款和该规范其他涉及坡体治理设计的条款，只出现“作用标准值的效应”而未出现“地震作用效应和作用效应标准组合”这一情况，该规范未要求地震基本烈度为7 度以上地区永久坡体及其支护结构地基稳定性验算考虑地震工况。 这样做是不正确的，因为一般工况与地震工况下作用组合情况及稳定安全系数取值不同，一般工况下稳定并不总是代表地震工况下稳定。

该款也未要求地震基本烈度为7 度以上地区永久坡体支护结构抗倾覆和抗滑移稳定性验算考虑地震工况， 但这并无不妥，坡体支护结构设计确实无需进行抗震强度验算，对此专题报告之一已有详细论述。

为此， 笔者主张对地震基本烈度为7 度以上地区永久坡体及其支护结构地基进行抗震稳定性验算。

4.3 安全系数取值

《地基通用规范》第7.2.3 条第1 款未给出坡体及其支护结构稳定性验算所需的稳定安全系数的具体值或定性要求，这是不妥的。

（1） 在此情况下，稳定安全系数即使取1.001 或者1.01 也没有违反《地基通用规范》的规定，而这样取值时，至少对坡体及其支护结构地基而言工程安全度是明显不够的。 也许有人认为，稳定安全系数取值可以由其他标准确定。 但这一认识是不正确的。

一方面，《地基通用规范》留下坡体及其支护结构稳定安全系数取值这个空白，意味着该规范对边坡工程和基坑工程中用安全系数法设计的部分没有给出其前言所称的 “保障……工程安全……的控制性底线要求”， 给出不含安全系数具体值或定性要求的公式（7.2.3）只是要求坡体及其支护结构稳定性验算采用安全系数法而已，离保障工程安全的控制性底线要求还差得很远。 如果保障工程安全的控制性底线要求有赖于其他标准，那么，制订《地基通用规范》是多余的。

另一方面，在《地基通用规范》对边坡不划分安全等级的情况下，《建筑边坡工程技术规范》（GB 50330—2013）按边坡工程安全等级提供的边坡稳定安全系数无法继续使用。

（2） 《地基通用规范》采用地基（桩基）承载力特征值概念和允许应力法进行地基（桩基）承载力验算，而确定地基（桩基）承载力特征值都涉及由地基（桩基）极限承载力标准值与安全系数相除，也就是说，《地基通用规范》对地基（桩基）承载力验算基本上明确了承载安全系数。 因此，对锚杆和土钉承载力验算不给出锚杆和土钉承载安全系数也与该规范地基（桩基）承载力验算方面的做法不匹配。

为此，笔者主张给出坡体及其支护结构稳定性验算所需的稳定安全系数取值要求，至少应给出如下取值原则：

（1） 相同条件下，坡体及其支护结构地基抗滑稳定安全系数应随治理工程重要性等级的提高而提高；

（2） 相同条件下，永久坡体及其支护结构地基抗滑稳定安全系数应大于临时坡体及其支护结构地基抗滑稳定安全系数；

（3） 相同条件下，一般工况坡体及其支护结构地基抗滑稳定安全系数应大于地震工况坡体及其支护结构地基抗滑稳定安全系数，且不应小于1.1；

（4） 相同条件下，抗变形挡墙抗倾覆和抗滑移稳定安全系数应大于抗失稳挡墙抗倾覆和抗滑移稳定安全系数；

（5） 挡墙抗倾覆和抗滑移稳定安全系数不应随治理工程重要性等级、设计使用年限和工况的变化而变化。

5 结论与建议

5.1 《地基通用规范》在坡体及其支护结构抗滑稳定性验算方面存在的问题

（1） 在岩土体（坡体及其支护结构地基）抗滑稳定性验算方面：对基坑工程未要求进行基坑边坡抗滑稳定性验算；未提出坡体抗滑稳定性验算作用组合选择要求和验算结果满足要求的标准； 将支护结构地基稳定性验算误称为支护结构整体稳定性验算；对直线形滑面岩土体，排他性地推行没有确定值的抗滑力与滑动力之比不小于安全系数的验算要求； 对圆弧形滑面岩土体，事实上排他性地推行已逐步淘汰的唯一不考虑条间力的条分法——瑞典法；对既非圆弧形又非直线形滑面岩土体，事实上排他性地推行已经淘汰四十多年、抗滑力与滑动力之比无明显物理意义且无确定值的投影和法；不要求对地震基本烈度为7 度以上地区永久坡体及其支护结构地基进行抗震稳定性验算。

（2） 在挡墙抗倾覆和抗滑移稳定性验算方面：将挡墙抗倾覆力矩归入土的抗力；将由墙式部分与锚杆组成的支护结构中墙式部分抗倾覆和抗滑移稳定性称为支护结构抗倾覆和抗滑移稳定性；排他性地推行没有确定值的抗倾覆力矩与倾覆力矩之比和抗滑力与滑动力之比不小于安全系数的验算要求。

（3） 在上述两个方面即岩土体（坡体及其支护结构地基）抗滑稳定性验算及挡墙抗倾覆和抗滑移稳定性验算方面：对所用荷载是分项系数为1.0 的荷载设计值还是荷载标准值作出矛盾的规定；不给出坡体及其支护结构稳定性验算所需的稳定安全系数取值要求。

上述情况有的有工程安全之忧，有的强制性要求技术人员犯概念性错误和采用落后甚至早已淘汰的技术，有的造成执行和监督执行（判断是否违反强制性条文）的困难和混乱。 这些都是在全文强制的规范中不应出现的。

5.2 笔者主张

（1） 对基坑工程要求进行基坑边坡抗滑稳定性验算；提出坡体抗滑稳定性验算作用组合选择要求；将支护结构整体稳定性改称为支护结构地基稳定性； 不将挡墙抗倾覆力矩归为土的抗力；将支护结构抗倾覆和抗滑移稳定性改称为挡墙抗倾覆和抗滑移稳定性； 将稳定性验算所用荷载是分项系数为1.0 的作用设计值还是作用标准值的矛盾规定统一为作用标准值。

（2） 对岩土体（坡体及其支护结构地基）抗滑稳定性验算，引入抗滑稳定系数概念；定义抗滑稳定系数为抗剪强度参数调整系数即滑面抗剪强度与剪应力之比；要求抗滑稳定系数不小于抗滑稳定安全系数；要求对地震基本烈度为7 度以上地区永久坡体及其支护结构地基进行抗震稳定性验算。

（3） 对挡墙抗滑移和抗倾覆稳定性验算，分别引入挡墙抗滑移和抗倾覆稳定系数概念；要求挡墙抗滑移和抗倾覆稳定系数分别不小于挡墙抗滑移和抗倾覆稳定安全系数；分别定义挡墙抗滑移和抗倾覆稳定系数为墙底抗剪强度参数调整系数和挡墙重度调整系数。

（4） 给出坡体及其支护结构稳定性验算所需的稳定安全系数取值要求，至少给出如4.3 节所述的取值原则。

（5） 对挡墙背后全为低粘聚力土且不视为坡体的情形，要求挡墙抗滑移和抗倾覆稳定安全系数随挡墙重要性等级变化，并要求进行永久挡墙抗震稳定性（包括地震工况下抗滑移和抗倾覆稳定性）验算。