基于参考向量的自适应约束多目标进化算法

史非凡，史旭华

（宁波大学信息科学与工程学院，浙江宁波 315211）

0 引言

目前，多目标进化算法（Multi-Objective Evolutionary Algorithm，MOEA）在工程优化领域中的应用展现出了其高效的计算能力及优异的算法性能。它大致分为三类：第一类是基于帕累托支配关系的算法。在该类型的多目标优化算法中，解的选择策略是基于帕累托（Pareto）支配关系，同时采用特殊的环境选择策略（小生境策略，聚类算法等）来同时保证解的收敛性及分布性。典型算法是由Deb 等［1］改进的NSGA-II（Non-dominated Sorting Genetic Algorithm II）。此外Hua 等［2］提出了一种结合聚类方法的多目标优化算法CA-MOEA（Clustering-based Adaptive MOEA），该算法对当前最优种群进行聚类，通过聚类中心来选择进入下一代的解，以保证解的分布性，在不规则的前沿面上展示出了良好的效果。第二类是基于性能指标的算法，为了对比MOEA 的性能，一些性能指标被提出用于定量地评价算法得到的种群质量，通过对其性能指标的评估来选择进入下一代的解。AR-MOEA（MOEA with Reference point Adaptation）采用一种改进的反向世代距离（Inverted Generational Distance，IGD）指标及自适应的参考点来进行环境选择［3］。第三类是基于目标分解的算法。该类算法的核心思想是生成一组均匀分布的权重向量，通过聚合函数将多目标问题转化为多个标量子问题，并且权值向量本身的均匀分布保证了解分布性。基于分解的多目标进化算法（MOEA based on Decomposition，MOEA/D）［4］中给出了三种聚集函数，即权重和方法（Weighted Sum）、切比雪夫方法（Tchebycheff）和基于惩罚的边界交叉（Penalty-based Boundary Intersection，PBI）方法。PBI 方法的参数可以通过设置近似于前两种方法，目前一般都采用PBI 方法。在此基础上Jain 等［5］结合非支配排序及可行性法则提出了C-MOEA/D（Constraint-MOEA/D）来处理约束多目标优化问题（Constrained Multi-objective Optimization Problem，CMOP）。MOEA/D-AWA（MOEA/D with Adaptive Weight vector Adjustment）［6］中通过权值向量的转换改进了Tchebycheff 方法，它能获得和PBI 方法同样好的分布性。进一步地，RVEA（Reference Vector guided Evolutionary Algorithm）是为了解决高维多目标优化问题而提出来的，该算法提出了一种全新的聚集函数APD（Angle Penalized Distance），并且能在种群迭代过程中重建参考向量，计算速度及求得解的精度都很出色［7］。

在过去的20 年中，多目标进化算法在解决无约束的多目标优化问题上非常成功，但是当使用其处理CMOP 时需要合适的约束处理技术来处理等式约束及不等式约束。常用的约束处理技术可以大致分为两类：第一类方法同时处理目标及约束，例如罚函数法［8］和多目标优化方法［9］等。罚函数法通过惩罚因子的方法将约束优化问题转化为无约束优化问题。这类方法的主要问题就是惩罚因子的设置，然而对于不同的CMOP，调整惩罚因子是比较困难的。多目标优化方法是将约束转化为问题的一个目标，是原本m个目标的n个约束优化问题转化成m+n个无约束优化问题。第二类方法分别处理目标及约束，代表性的方法是Deb［10］提出可行性法则。此外还有一种ε约束处理方法［11］，该方法在解的约束违规小于阈值ε时，将其视为可行解。当ε=0 时，该方法等同于可行性法则。

基于对工程优化领域上解的不确定性和约束的复杂性，本文提出一种基于参考向量的自适应约束多目标进化算法（Adaptive Reference Vector based Constrained MOEA，ARVCMOEA），通过分阶段分类别的混合计算意图在各种形态的CMOP 上均获得较好的搜索性能。算法初始阶段对种群进行分类：一类不考虑约束条件，使种群可以跨越约束范围较大或约束值大的区间，也能加快收敛速度；另一类考虑约束并且对分布性提出更为严格的要求，使种群保持良好的分布性。算法在最后阶段进行局部搜索，根据当前支配解比例及对应的参考向量构建局部分布性强化区域。通过降低非支配解对应参考向量的分布性要求构建强化搜索区域，增强算法的搜索能力；同时，动态地更新参考向量所属区域，从而在保证种群分布性的前提下提高算法的搜索能力。

1 相关背景

1.1 约束多目标优化

一个约束多目标优化问题（CMOP）可以描述为：

其中：F(x)是决策空间到目标空间的映射，是m维向量，m为目标个数；gi(x)和hj(x)分别为第i个不等式约束和第j个等式约束；p为不等式约束数量；q为等式约束数量；x=(x1，x2，…，xn)T是决策变量，是一个n维向量，n是决策变量个数。

一般解的约束违反值由式（2）计算：

其中：ε是无穷小值，一般ε=1×10-6用来将等式约束转化为不等式约束。

1.2 聚合函数

聚合函数通过对解相较于参考向量的几何关系来评价其优劣。MOEA/D 中包含三种聚合函数，分别是Weighted Sum、Tchebycheff 与PBI 方法。本文采用的是RVEA 中一种基于角度的聚合函数的思想，该函数通过当前解与参考向量的夹角进行适应度惩罚，并在此基础上进行一些微调，其标量子问题可以描述为：

其中：

进一步地标量的子问题的适应度函数结合约束的惩罚项可以概括成：

1.3 CMOP的困难点

1）分布性的困难。通常这类的帕累托最优前沿（Pareto Front，PF）是不连续的或者因较大的不可行域造成一小部分比其余部分PF 难以被搜索到。

2）可行区间的困难。通常是因为极小的可行域难以被搜索到或者极大的不可行域阻挡了搜索方向因而陷入局部最优。

3）收敛性的困难。CMOP 阻碍了MOEA 向PF 的收敛，即约束阻挡了算法的收敛，在进化过程中很难实现最小化。

2 参考向量自适应的多目标约束进化算法

图1（a）为算法C-MOEA/D 在测试函数DASCMOP5［12］上的局部种群分布情况。常规的基于分解的算法采用单一聚合函数，这样会因为标量化问题的收敛性、分布性及约束违反值的权重分配问题导致部分个体在约束边缘聚集，无法对种群进化提供有效帮助。图1（b）为NSGA-II 在测试函数C1-DTLZ1 上的种群分布情况，种群因一个较大的不可行域而无法收敛至最优。这两类难点在解空间上存在于不同的位置，极大的不可行域存在于种群的收敛过程中，而PF 的不连续是集中在PF 附近。即可以在算法起始优先使种群跨越约束快速收敛至PF 附近，然后再优化种群分布性。

图1 C-MOEA/D及NSGA-II算法在两种特殊的测试函数上种群的分布情况Fig.1 Population distribution of C-MOEA/D and NSGA-II algorithms on two special test functions

MOEA 对于CMOP 的难点主要集中在极大的不可行域造成的算法陷入局部最优及PF 不连续造成的分布性差。

本文算法将参考向量分为两类：一类在算法全局采用同一聚合函数以保证算法稳定性；另一类参考向量根据阶段不同变化聚合函数及约束处理方法以指导种群进化。在算法初始通过部分无约束计算的种群指导种群跨越不可行区间，有效地搜索可行域，提高种群收敛速度；在算法后期采用弱分布性的聚合函数，通过扩大对种群进化没有帮助的参考向量的搜索范围，为种群分布性提供帮助，增强算法搜索能力。

2.1 参考向量的分类及更新

基于分解的多目标优化算法首先要生成均匀分布的与种群数量N相同数量的参考向量。本文将参考向量等分成主参考向量及辅助参考向量两类，并采用均匀分布方式，见图2。主参考向量主要为了保证算法稳定性，全局保持同一聚合函数，并且侧重分布性。

图2 主参考向量及辅助参考向量分布示意图Fig.2 Schematic diagram of distribution of main reference vectors and auxiliary reference vectors

在第一阶段，辅助参考向量在计算适应值函数时不考虑约束，主要作用是指导种群越过较大的不可行域，并且能够加速算法收敛；而主参考向量考虑约束且强调分布性使种群可以尽可能地保存分布性的信息。当主参考向量在无约束的情况下近似收敛时，算法进入第二阶段。第二阶段是柔性过渡阶段，全部参考向量均考虑约束。由于当前辅助参考向量有可能存在于不可行域中，突然增加约束会造成该部分解直接被可行域中解取代，不利于算法收敛，影响算法搜索能力。本文对约束进行适当降权，适应值函数自适应调整权重，使辅助参考向量有一个反向的搜索能力。当全部解均是可行解或一定代数后算法进入第三阶段，该阶段试图解决因约束导致的PF 不连续造成的部分参考向量对应的解始终是远离PF 的非支配解，无法对最终的收敛及分布性提供帮助的问题。所以在第三阶段将当前种群中非支配解所对应的参考向量记为非支配参考向量即主参考向量，其他向量记为支配参考向量即辅助参考向量，区别在于辅助参考向量在适应度计算时减少其角度的惩罚项，使搜索范围增大，提高算法搜索能力。

三个阶段的参考向量分类用逻辑矩阵mark进行二分类。主参考向量逻辑值始终为1，本文要注意的是在第二阶段的过渡开始时重置全部参考向量的逻辑值为1。第三阶段设置当前支配解所对应参考向量为主参考向量，其他向量为辅助参考向量，并进行动态更新。整体更新规则详见算法1。

2.2 适应值计算及约束处理

在适应值计算方面，主参考向量作为保证算法稳定性的基础，全局采用同一适应值函数，侧重于对分布性的要求。而辅助参考向量作为辅助指引，本文则侧重其收敛性，并且放宽其多样性要求，从而提高收敛速度及搜索范围。本文通过式（5）中的α参数控制，主参考向量对分布性要求高，α默认取2，在几何意义上近似于PBI 聚合函数。辅助参考向量加速收敛以及放宽搜索区间α默认取10。以主参考向量为例，当前解与当前参考向量的夹角是当前参考向量与最邻近参考向量夹角的2 倍时惩罚值为2。基本上可以使个体在参考向量左右4 个角度附近进化，从而保留其分布性信息。

同样在不同阶段算法采用不同的约束处理方法：第一阶段中辅助参考向量计算时不考虑约束来指导种群跨越不可行域。主参考向量计算采用罚函数法，在保证分布性的前提下尽可能地在空间中进行搜索。第二阶段中所有向量均增加约束要求，并且整个种群要向着可行域进化来为第三阶段中支配向量的局部搜索准备。值得注意的是当算法进入第二阶段时突然增加的约束会导致大量在约束空间的解会被邻近参考向量的可行解直接取代，会降低算法的搜索能力及稳定性。所以第二阶段的适应值函数对约束进行了限制：

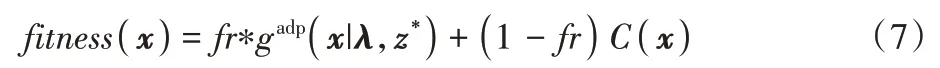
其中：fr为可行解占比，当种群不可行解占比大时约束惩罚值占主导地位，使个体快速向可行域进化。当可行解占比高时，适应值计算主要取决于聚合函数值。在第三阶段中对于约束的处理变更为可行性规则，使种群充分地在可行域内搜索。

2.3 主参考向量指导的父代选择

一般多目标优化算法会使用标准的遗传算法（Generic Algorithm，GA）作为搜索算法，基于分解的多目标优化算法会在相邻区间内随机选择两个个体作为父代，通过GA 生成一个子代进行比较。本文对父代的选择进行了改进，设置了概率Pm通过主参考向量占比来决定。

算法2 通过rand随机一个0 到1 的随机数，在第一阶段时主参考向量占比为0.5，则pm为0.5，则有一半的概率子代会从主参考向量对应的子代中选取，而另一半概率从全部个体中随机选取，那么子代均为辅助参考向量对应个体概率为0.25。在第二阶段中pm为1，这里则均匀随机产生父代。第三阶段中若主参考向量占比高则pm小，父代大概率在主参考向量对应的解中产生；若主参考向量占比低则在种群中随机产生。这样两个父代均是辅助参考向量对应解的概率为（1-pm）2，即降低了父代均为辅助参考向量对应个体的概率，增强了算法稳定性。

2.4 算法整体流程

整个算法流程基于MOEA/D 框架，结合算法1 参考向量跟新机制及算法2 的主向量指导的父代选择机制，算法的整体框架如下：

初始化种群P，初始化标记矩阵mark，邻居索引矩阵B及一些相关参数。可调参数NI代表每次判断是否更新mark的代数间隔，可以根据设置的最大进化代数来设置，过小的NI可能造成第一阶段的提前收敛，过大的NI则会导致阶段转换困难造成计算浪费，本文默认NI=50。算法第7）～15）行是解的更新过程，第9）行为算法2 父代的选择策略，采用了标准GA 的交叉及多项式变异来产生子代。第10）～13）行是计算个体适应度的过程，根据mark的不同使用不同的适应度函数及约束处理方法。第16）～17）行更新mark。当达到最大代数后算法返回最终的种群P。

3 实验与结果分析

为了验证算法在解决CMOP 上的性能，与算法NSGA-II［1］、C-MOEA/D［5］、MOEA/D-DAE（MOEA/D with Detect-And-Escape strategy）［13］和 CCMO（Coevolutionary Constrained Multi-objective Optimization framework）［14］在不同的测试函数DTLZ［5，15］、DASCMOP［12］和MW［16］上进行了比较。实验在多目标优化平台PlatEMO［17］实现，其中算法所涉及到使用的GA 均采用平台默认参数。

根据测试函数的难易程度设置终止条件，带有约束的DTLZ 及MW 的24 个测试函数终止代数为800，DASCMOP 的6 种测试函数的终止代数为1 000。DASCMOP1～3 的参数设置为0、0.5、0.5，DASCMOP4～6 的参数设置为0.5、0.5、0.5。

表1 显示了NSGA-II、C-MOEA/D、MOEA/D-DAE、CCMO和本文ARVCMOEA 算法在10 个带有约束的DTLZ 测试函数、6 个DASCMOP 测试函数及14 个MW 测试函数上运行20次后计算得到的IGD 以及GD 值的平均值和标准差。IGD 通过在测试函数PF 上采样的10 000 个参考点进行计算，可以看出本文算法在大多数测试问题上结果上更精确。其中在DTLZ 测试函数PF 相对简单，C-DTLZ 为单一约束，DC-DTLZ为复杂约束，可以看到算法可以很好地处理单一种类约束；在DC-DTLZ 测试函数相较于其他算法结果更出色，原因在于起始阶段可以快速跨越不可行域，使种群快速到达PF 附近；在部分函数上IGD 数值无法达到最优是因为PF 不连续程度过大，算法后期大量参考向量对应的个体仍然存在于不可行域中，即使其作为辅助参考向量得到的可行解占比仍不如通过支配关系得到解的分布性好。DASCMOP 测试函数为多种约束混合，算法仍表现出良好的稳定性。MW 测试函数则是在无约束条件下收敛更为困难，一定程度上影响了算法起始阶段的效果，降低了算法收敛速度。在MW4、MW8 及MW14 三个目标的测试函数下没有达到最优，原因在于辅助参考向量在最后搜索阶段提供搜索帮助时，没有办法使种群均匀分布，在两个目标时不均匀分布的效果被弱化了，目标数越多这个部分的不均匀性越高。然而这本身也是为了优化基于分解的多目标优化算法在不连续前沿的弊端，同时增强了搜索能力。一般IGD 指标主要衡量种群分布性，而世代距离（Generational Distance，GD）指标值主要衡量种群的收敛性。通过五种算法在不同的30 个测试函数上的GD 指标值可以看出：ARVCMOEAD 在DTLZ 及MW 问题上收敛性较好，在DASCMOP 上结果较CCMO 略差。DASCMOP 的PF 不连续且间断多，在一定程度上影响了主参考向量的个数，这样就导致算法在相同代数在收敛性上的计算次数会降低。通过对GD 及IGD 的结果与标准差比较可以展示出算法的良好的稳定性及搜索能力。

表1 五种算法在DTLZ、MW及DASCMOP上的IGD及GDTab.1 IGD and GD of five algorithms on DTLZ，MW and DASCMOP

续表

图3 展示了NSGA-II、CMOEA/D、MOEA/D-DAE、CCMO及ARVCMOEAD 在DC2-DTLZ3、DASCMOP6 及MW8 上的20次运算得到最优IGD 的非支配解分布比较。在DC2-DTLZ3测试函数上可以看出ARVCMOED 在均匀分布的PF 上仍具备基于分解的MOEA 的良好的多向性分布，并且可以很好地跨越不可行区域，而在DASCMOP6 上过于分散的PF 上也能够有较好的搜索能力并且搜索到了其他算法没有搜索到的解，说明算法具备良好的搜索能力。

图3 五种算法在DC2-DTLZ3、DASCMOP6及MW8上的20次运算得到最优IGD的非支配解分布比较Fig.3 Non-dominated solution distribution comparison of optimal IGDs obtained by five algorithms after 20 runs on DC2-DTLZ3，DASCMOP6 and MW8

表2 给出算法在三个系列函数上的20 次计算的平均计算时间，结果表明NSGA-II 的耗时最短，MOEA/D-DAE 耗时最长。其中本文算法与C-MOEA/D 采用相同的搜索策略，算法时间复杂度基本一致，但是由于部分约束计算并且增加了阶段及参考向量更新机制，所以计算时间会比C-MOEA/D稍长。

表2 五种算法在三个系列测试函数上的平均计算时间 单位：sTab.2 Average computing times of five algorithms on three series of test functions unit：s

图4 给出了五种算法的GD 收敛曲线。可以看出在拥有较大不可行域的C1-DTLZ3 及MW9 测试函数上ARVCMOEA收敛性更好。在DASCMOP5 上在起始时收敛速度最快，但是中间一段阶段没有继续收敛，是由于当前约束处理方法导致的部分解可能停留存在于不可行域中，在进入最后阶段时继续收敛。在MW9 测试函数解空间中绝大部分是不可行域，这样ARVCMOEA 在起始阶段由于主参考向量对分布性信息的要求及约束处理策略，会略微影响其收敛速度。同样由于这部分的分布性信息使算法在下一个阶段可以更快地得到最优的收敛效果。

图4 五种算法在C1-DTLZ3、DASCMOP5及MW9上的GD收敛曲线Fig.4 GD convergence curves of five algorithms on C1-DTLZ3，DASCMOP5 and MW9

4 结语

本文针对复杂种类的CMOP 提出了基于参考向量自适应调整的约束多目标进化优化算法。算法将参考向量分为主参考向量和辅助参考向量，通过自适应调整辅助参考向量来辅助算法解决不同种类的约束，而主参考向量全局不变以保证算法的合理性及稳定性。算法通过在各个阶段调整父代选择策略及约束处理方法算法，在维持基于分解的MOEA在多样性分布上的优势的前提下，提高了解决约束的能力及解的搜索能力，并且改善了基于分解的MOEA 对于不连续PF 的处理能力，结果在多个测试函数上均取得了更优的结果。此外，若能提高算法在无约束条件下的收敛速度及搜索能力，则能进一步提高本文算法的性能。对于进化算子的选择也能对算法在特定测试函数上的计算有较大帮助，后续可以通过结合性能优异的MOEA 来提高算法性能。