变精度邻域等价粒的邻域决策树构造算法

谢 鑫，张贤勇*，王旋晔，唐鹏飞

（1.四川师范大学数学科学学院，成都 610068；2.四川师范大学智能信息与量子信息研究所，成都 610068）

0 引言

粗糙集［1］是处理不确定性理论的重要工具，广泛应用于人工智能、数据挖掘、决策分析等领域［2-5］。经典粗糙集主要使用等价关系划分粒结构，因此更适合于处理离散性数据，在处理连续性数据时往往需要进行数据预处理，也就是对数据离散化，这将导致部分信息缺失。为了解决这个问题，粗糙集理论被扩展为邻域粗糙集理论［6-7］。邻域粗糙集引入了邻域关系和邻域决策信息系统，对邻域信息粒子进行邻域粒化和粗糙逼近，扩大了粗糙集理论的应用范围。邻域决策信息系统是邻域粗糙集理论构建的基本形式背景，其上的不确定性度量和样本分类体系构建值得被探讨。

分类算法对于数据分析具有重要的意义，决策树是导出决策规则的一种常用分类方法。决策树算法具有分类速度快、精度高、规则简单易懂等优点，因此其相关的归纳算法和知识发现在机器学习中有着广泛的研究和应用［8-13］。经典的决策树算法包括基于基尼指数的决策树算法CART（Classification And Regression Tree）、基于信息熵的决策树算法ID3（Iterative Dichotomiser 3）、基于信息增益率的决策树（C4.5）算法等。CART 算法是一种经典的算法，每个节点的划分按照能减少的杂质的量来进行排序，杂质度量方法常用Gini 指标［14］。ID3 算法同样是一种经典的决策树算法［15］，它主要以信息增益为节点生成的属性度量准则，以属性上的等价关系为节点分裂规则，表现出了较好的样本分类效果，但只能处理离散型数据。在ID3 算法基础上，可以处理连续型数据的C4.5 算法［16］被Quinlan 提出。不同于ID3 算法，信息增益率被用作C4.5 算法节点生成的度量准则。CART 算法和ID3 算法两种传统的决策树生成算法利用了信息论中的信息测度，C4.5 算法在处理连续型数据过程中要对数据进行离散化，这增加了算法的时间复杂度和空间复杂度，并且可能造成决策信息系统的信息丢失，不利于样本分类。

为了克服决策树构造算法在面对连续型数据表现出的信息丢失、算法准确度不高等缺点，邻域决策信息系统上的决策树构造算法首次被提出。邻域决策信息系统具有其信息粒结构表示的独特性，因此，邻域等价粒被探讨，进而变精度邻域等价粒被挖掘。基尼指数被扩展至变精度邻域等价粒结构上，建立邻域基尼指数不确定性度量，并探讨度量的相关性质。最后，基于邻域基尼指数度量构造决策树启发式算法，采用来源于UCI 的数据集进行实验，统计了决策树算法的准确度和叶子数等指标，与经典的CART 算法、ID3 算法、C4.5 算法以及最新文献［17］中融合信息增益和基尼指数IGGI（combining Information Gain and Gini Index）算法作对比分析。

1 基本知识

L=(U，C∪D，V，f)为一个决策信息系统，常简记为决策表DT=(U，C∪D)。其中：U表示有限非空样本全集；C={a1，a2，…，a|C|}表示有限非空条件属性全集；D表示决策属性；V=表示属性值的集合，Vc表示属性c的属性值范围，即属性c的值域；f：U×B→V(B⊆C)表示一个信息函数。

1.1 邻域决策信息系统

经典粗糙集理论建立于等价关系基础上，对具有连续值信息系统进行信息的不确定性度量和对数据做特征选择时，往往需要离散化，这将造成信息的丢失，邻域粗糙集理论的探讨具有意义［5］。

给定一个决策表DT=(U，C∪D)，其中C={c1，c2，…，cn}={cj|j∈{1，2，…，n}}。对∀B⊆C，B可以表示为：

则样本x、y在B上的距离函数为：

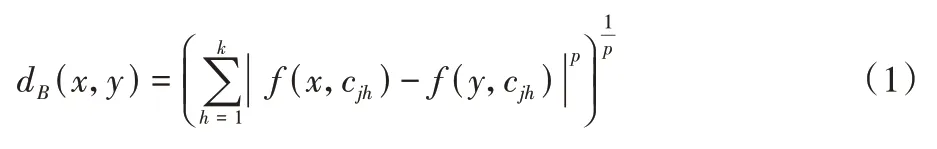
特别地，当p=1 时，此距离被称为Manhattan 距离。本文主要采用Manhattan 距离。由距离函数，∀x∈U在B上的δ-邻域（类）为：

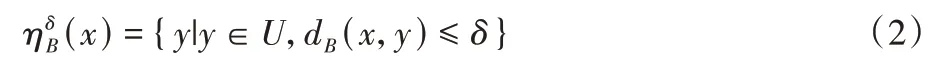
为了区分一般的信息系统，将邻域决策信息系统（Neighborhood Decision information System，NDS）表示为：NDS=(U，C∪D，V，f，d，δ)，与一般信息系统相比增加了距离函数d和邻域半经δ。

命题1NDS=(U，C∪D，V，f，d，δ)为一个邻域决策信息系统，则如下性质成立：

1）若δ1≤δ2，则∀x∈U有；若δ=0，则=[x]B。

2）若A⊆B，则∀x∈U有。

命题1 揭示了邻域与半径阈值以及属性集大小的关系，其中当邻域半径δ=0 时，样本的邻域退化为与它等价的样本集。

1.2 三种经典决策树算法

决策树是一种自顶向下的树型分类器，通常由叶子、非叶节点、根节点三部分构成。它首先进行根节点优选，非叶节点根据如下的分裂函数h(x，ai)进行分裂：

其中：ai∈C为单属性；x(ai)为样本x在属性ai上的取值；αi为间值，根据属性ai的划分而取值。样本通过分裂函数h(x，ai)被分配到决策树的每片叶子中。例如：h(x，ai)=0代表最左边的叶子，h(x，ai)=1 代表最右边的叶子，而其余的代表中间的叶子。

基尼指数能表征数据的不均衡分布，其诱导的CART 算法可以构造分类树。

定义1［14］在决策表DT=(U，C∪D)中，决策分类U/D的基尼指数为：

D关于B⊆C的基尼指数为：

其中：Gini(Bi)=1 -，U/B={B1，B2，…，Bn}。

CART 算法采用基尼指数来实施属性优选，由此建立分类树。此外，CART 算法还可以构建回归树。

来源于信息理论的信息熵关联于系统信息含量，能够表征样本集合的不确定性，由此可以得到经典的决策树归纳算法ID3［15］。

定义2［15］在决策表DT=(U，C∪D)中，决策分类U/D={D1，D2，…，Dm}信息熵为：

其中：H(Bi)=。进而，条件属性B的信息增益为：

gain(D，B)=H(D)-H(D|B)。

ID3 算法遍历每一个属性特征，选择具有最优信息增益的特征来划分数据，由此递归构造决策树。ID3 算法操作简单，但容易涉及偏移性与低精度，后续具有较多改进算法，包括C4.5 算法等。

定义3［16］在决策表DT=(U，C∪D)中，D关于条件属性B⊆C的信息增益率被定义为：

其中：split.info(B)=。

C4.5 是用信息增益比率来作为选择分支的准则。信息增益比率通过引入一个被称作分裂信息（Split information）的项来对信息增益进行归一化处理。C4.5 弥补了ID3 中不能处理特征属性值连续的缺陷，但是，对连续属性值需要扫描排序，这使C4.5 性能下降。

2 变精度邻域等价粒邻域决策树

2.1 变精度邻域等价粒

定义4以下关系被称为B⊆C上的邻域等价关系：

其中：δ∈[0，1]为邻域半径；表示样本*在B上的δ-邻域。基于邻域等价关系，诱导出邻域等价划分：

定义1 表明当两个样本的邻域完全相等时，这两个样本被看作等价的。然而，这样的条件太过严格，即现实数据中很难找到两个邻域完全一样的样本，因此，变精度邻域等价粒被提出。

定义5NDS=(U，C∪D，V，f，d，δ)为邻域决策信息系统，x，y∈U在属性B下的邻域相似度定义如下：

以下关系被称为B⊆C上的变精度邻域等价关系：

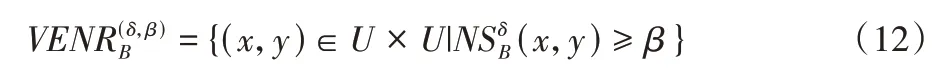
其中：δ表示邻域半径阈值；β表示变精度阈值。基于变精度邻域等价关系，诱导出变精度邻域等价粒结构：

粒结构中，常常伴随着粒粗细的比较。变精度邻域等价粒结构的粗细定义如下。

命题2NDS=(U，C∪D，V，f，d，δ)为邻域决策信息系统，以下性质成立：

1）若δ1≤δ2，则；

2）若β1≤β2，则。

证明

推论1NDS=(U，C∪D，V，f，d，δ)为邻域决策信息系统，0 <δ1≤δ2≤…≤δn≤1、0 <β1≤β2≤…≤βn≤1 分别为邻域半径阈值增链和精度阈值增链，则有：

命题2 和推论1 简要探讨了变精度邻域等价粒结构的一些性质。自然地，基于粒结构可构造上面的度量函数。

2.2 变精度邻域基尼指数度量

在经典的决策树构造算法中，基尼指数被用作决策树节点分裂的度量函数，后被发展为互补熵、互补条件熵、互补互信息等。本文中，基尼指数被扩展为邻域基尼指数，以此度量邻域决策信息系统的不确定性，进而构造面向连续性数据的决策树分类算法。

定义7NDS=(U，C∪D，V，f，d，δ)为邻域决策信息系统，B⊆C基于变精度邻域等价关系的邻域基尼指数为：

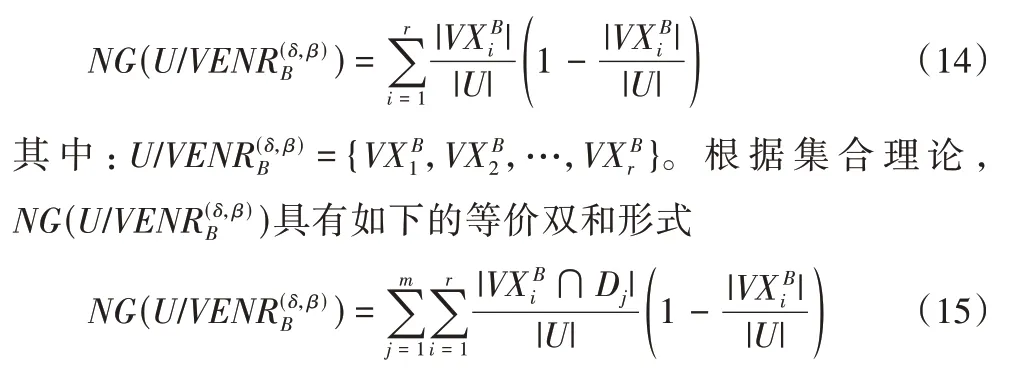
其中：U/D={D1，D2，…，Dm}。

定义8NDS=(U，C∪D，V，f，d，δ)为邻域决策信息系统，的邻域基尼指数为：

证明 设NG(x)=x(1 -x)，则NG(x)为一元二次函数，对称中心x=，定义域端点处取得最小值0。

决策树构造过程中，对数据不确定性的度量主要考虑决策属性D关于条件属性的不确定性量化。首先定义D关于单个粒的信息度量。

定义9NDS=(U，C∪D，V，f，d，δ)为邻域决策信息系统，D关于的邻域基尼指数为：取得最大值

因此，D关于条件属性B⊆C基于变精度邻域等价关系的邻域基尼指数为：

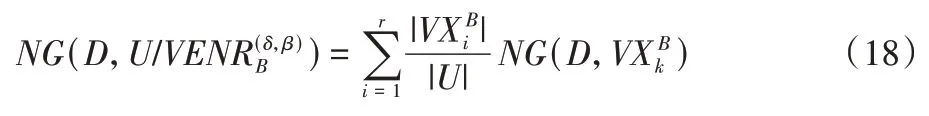
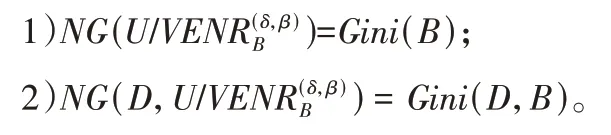
证明 当δ=0，β=1 时，变精度邻域等价关系就变成了一般等价关系，变精度邻域等价粒结构也就变成了一般等价粒结构，因此邻域基尼指数退化为一般基尼指数。

例1 表1 为一个连续性数据的邻域决策信息系统。其中U={x1，x2，…，x7}，C={c1，c2，…，c5}，U/D={{1，2，4，5}，{3，6，7}}。基于Manhattan 距离和取定δ=0.5、β=0.7，计算相关度量值，相关结果如表2 所示。表2 中“*”代表具体的粒结构，本例中主要为。现考虑δ=0，β=1 这种特殊情况，计算结果如表3 所示。

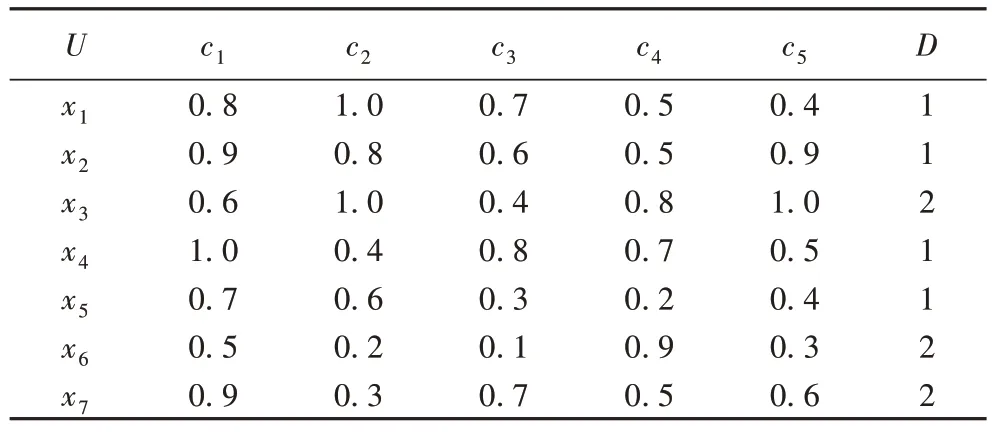
表1 实例决策表Tab.1 Example decision table

表2 δ=0.5、β=0.7时两种度量的函数值Tab.2 Function values of two measures with δ=0.5 and β=0.7

表3 δ=0、β=1时四种度量的函数值Tab.3 Function values of four measures with δ=0 and β=1

表3 表明当δ=0、β=1 时，NG(*)=Gini(c)和NG(D，*)=Gini(D，c)，这与命题1 符合。

决策树构造以NG(D，)为节点分裂的度量函数。

2.3 变精度邻域等价粒邻域决策树构建

决策树构建常常涉及到节点选择和树的分裂，根据邻域基尼指数度量函数构建邻域决策树算法。

算法1 涉及到将一个邻域决策信息系统分割为多个子决策信息系统，然后对每个子决策信息系统递归的执行操作，最终递归生成决策树。第1）步，遍历决策信息系统的所有单属性；第2）步，根据式（18）计算每个单属性的不确定性度量NG(D，)，并反演找出最优单属性，以此作为分裂节点属性。第3）～4）步，根据节点单属性诱导其上的变精度邻域等价粒结构，构造节点分裂产生树的分支，产生多个子决策信息系统。第5）步，对每个子决策信息系统递归执行第1）～4）步，判断算法终止条件，最终根据第6）步返回决策树。算法主要涉及到属性不确定性的遍历计算和子决策信息系统的递归划分，因此算法的时间复杂度和空间复杂度主要为Ο(|C||U|)。

邻域决策树算法与传统的ID3 算法、CART 算法、C4.5 算法有着类似的算法框架，但有着本质的区别。具体表现在：1）邻域决策树算法对叶子节点分裂的信息，采用邻域基尼指数度量，能从底层度量连续性数据。经典的三种算法度量函数均不可直接度量连续性数据，往往需要将数据离散化，伴随着信息的丢失。2）节点的分裂规则不一样。传统的ID3算法、CART 算法、C4.5 算法主要以样本的等价划分为分裂规则。邻域决策树算法的叶子分裂规则为变精度邻域等价粒结构，且可以通过调节精度阈值β来控制节点分支的粗细，当β=1 时，退化为邻域等价粒，意味着每个分支里面样本的邻域均相同。

3 数据集实验

本章将在来自UCI 数据库的连续性数据集上进行实验，验证算法的性能［18］，并与传统的ID3 算法、CART 算法和C4.5 算法进行对比性实验分析。考虑到ID3 算法、CART 算法面向的为连续数据集，所以需要先对数据进行离散化，再进行样本分类。数据离散化采用等距离划分方法［19］。等距离划分根据用户给定的区间数目K，将数值属性的值域[Xmin，Xmax]划分成距离相等的K个区间，每个区间的宽度为δ=(Xmax-Xmin)/K。实验数据集采用的UCI 数据集如表4 所示，它们的决策属性个数均为一个。其中ILPD 为数据集Indian Liver Patient Dataset 的缩写。

表4 UCI 数据集Tab.4 UCI datasets

决策树算法评价常常考虑算法准确度和叶子数两种评价指标。本文同样考虑这两种评价指标，其中叶子数由编程软件直接统计得到，算法准确度由式（19）计算：

其中：m为决策属性中的标签类别数；表示所有类别的样本数之和；TDj表示正确的被分为第j类的样本集；|·|表示集合的基数。

对数据集采用十折交叉法进行算法验证，得到相关结果如表5 所示。

经典的ID3、CART 对连续性数据进行样本分类时，需要进行数据离散化，而信息的丢失主要与离散化方法有关。本文采用的是等距离划分方法，区间数K的大小影响着树的准确度和叶子数。一般来说，K越大树的叶子数越多，准确度越高，样本分类更准确。然而，针对不同的数据集，找到合适的K值，是一件不容易的事。表5 中的信息表明，NDT 算法在不同数据集上面的算法准确度均有不同程度的提高，例如：相较于CART 算法准确率提升了0.232 3，其余算法也平均提升了20 个百分点左右。NDT 算法直接从底层度量连续性数据的信息，对样本的识别更准确。

表5 不同决策树算法的实验结果对比Tab.5 Comparison of experimental results of different decision tree algorithms

图1～2 展示了不同算法的准确度、叶子数的比较结果，结果表明：NDT 算法的准确度在大部分数据集上面均有明显提升，只有seeds、heart 和segment 上提升不明显；叶子数方面，NDT 算法CART 算法的叶子数较接近，NDT 算法有不同程度的提高但仍处于可接受范围，这是算法机制所导致。

图1 不同算法的准确度对比Fig.1 Accuracy comparison of different algorithms

图2 不同算法的叶子数对比Fig.2 Comparison of leaf number of different algorithms

4 结语

邻域决策树构造算法聚焦信息系统的底层信息度量，避免经典决策树算法针对连续性数据样本分类时造成信息丢失问题。挖掘信息系统的变精度等价粒结构，构建邻域基尼指数度量，最终诱发邻域决策树构造算法。实验结果表明，本文提出的邻域决策树算法准确度得到了明显的提高，算法具有有效性。