基于元强化学习的自动列车定速控制

颜罡赵斐然叶 锋吴俊博游科友

(1.中车株洲电力机车有限公司,湖南株洲 412000;2.大功率交流传动电力机车系统集成国家重点实验室,湖南株洲 412000;3.清华大学自动化系,北京信息科学与技术国家研究中心,北京 100084)

1 引言

随着铁路交通系统的迅速发展,高速、舒适的列车出行已成为人们迫在眉睫的需求.铁路系统的可靠性和效率主要取决于自动列车控制系统.该系统中运行着3个子系统,分别是自动列车监控系统、自动列车保护系统和自动列车运行(automatic train operation,ATO)系统[1].ATO系统是自动列车控制系统的关键部分,用于控制列车运行的各个阶段,例如:自动出发、加速、巡航、制动、精确停车、站间临时停车、自动折返等[2].其中,ATO系统的定速控制是一个基本问题,即在变化的列车线路条件下将列车稳定、快速地调节到给定速度.由于列车动力学系统固有的模型不确定性,以及由天气条件和列车线路条件引起的外部干扰[3-4],ATO系统的定速控制存在许多困难.其中,列车动力学模型的参数和干扰在实际中是多种多样的,并且很难用数据估计.此外,铁路路况条件随列车的行驶而频繁变化,例如,铁路斜坡等,从而要求控制策略能够适应路况变化.

传统的控制方法主要集中在时不变列车动力学模型的定速控制问题上,如:鲁棒控制[5]、最优控制[6]、预测控制[7]和滑模控制[2,8].文献[6]提出了一种使用新的局部能量最小化原理的最优控制方法,同时不考虑模型的不确定性和外部干扰.文献[7]设计了一种预测滑移控制器以实现最大的加速度,而在分析中忽略了由复杂的列车线路状况引起的外部干扰.文献[5]提出了一种鲁棒的控制方法来补偿模型的不确定性,而没有关注时变扰动的影响.文献[2]采用滑模控制器在线估计动力学模型的未知参数,而无需分析随时间变化的运行条件.

基于模型的控制器要么需要精确的动力学模型,要么需要时时估计未知参数.而实际上,由于复杂的操作环境,很难对动力学系统进行精确建模.外部干扰和未建模的动力学也给控制器的设计带来了困难.因此,有必要用无模型的方法得到控制器.在这项工作中,本文通过强化学习(reinforcement learning,RL)来学习控制器.RL旨在仅通过使用数据来解决马尔可夫决策过程(Markov decision process,MDP)问题.注意到列车在运行期间,诸如铁路坡度之类的铁路线条件一直在变化,这意味着列车动力学模型本质上是时变的,而基于RL的控制器仅适用于时不变模型.因此,无模型控制器必须能够自适应环境,即能够在合理的时间段内适应变化的铁路路况.为此,本文利用元学习框架来增强RL控制器在不同列车线路条件下的通用性,从而使其仅使用少量训练样本即可适应新的铁路路况,这构成了用于列车定速控制的元强化学习(Meta-RL)[9].RL已成功应用于一些连续控制问题,包括自动水下航行器(automatic unmanned vehicle,AUV)[10]、移动机器人的路径规划[11]、基于视觉的机器人运动控制[12]等.文献[13-14]研究了用于连续控制问题的Meta-RL,并在仿真环境中验证了其性能.

Meta-RL的目标是学习一种初始的参数化控制策略(或策略),以使其仅通过学习少量样本可以在新的RL任务上发挥最大的性能.元学习的基本思想是,策略中存在一个内核表示形式,该形式广泛适用于许多任务,因此,对参数进行微调就可以在新任务上产生良好的结果.为了将列车定速控制问题化为Meta-RL问题,本文将时不变环境下的学习任务定义为求解一个平稳马尔可夫决策过程MDP.对于定速控制问题来说,智能体依据策略采取行动,将其作为ATO系统的控制输入,然后状态根据动力学模型改变,并观察到当前的损失函数.本文根据系统的动力学设计MDP的状态,并将损失函数定义为速度误差和能耗的线性组合.通过适当地离散化列车线路路况,本文在解决一系列RL任务的情况下,建模了列车在变化路况下的定速控制问题.然后,采用元学习框架来学习自适应控制器,该控制器能够仅通过使用样本来适应新的MDP.本文通过仿真说明,由Meta-RL学习的无模型控制器性能良好.

本文的主要贡献概述如下:

1) 本文率先使用基于RL的控制器来解决ATO系统的定速控制问题;

2) 本文应用元学习来训练自适应控制器,使得该控制器能快速适应变化的环境.

本文的其余部分组织如下:在第2节中,作者提出了ATO系统的定速控制问题;在第3节,作者将定速控制问题建模为一系列平稳MDP问题;第4节采用Meta-RL框架对MDP问题进行求解并得到自适应控制器;第5节对元强化学习算法的实现细节进行了讨论;第6节进行了仿真以验证Meta-RL算法的有效性.

2 问题建模

本节描述了列车控制系统和定速控制问题.

2.1 自动列车控制

列车自动控制系统旨在实现对列车的高效、准确的控制.其由3个子系统组成,即ATO系统,自动列车监管(automatic train supervision,ATS)系统和自动列车保护(automatic train protection,ATP)系统,请参见图1.ATO系统在列车中起着至关重要的作用,它负责管理列车运行的几乎所有控制问题,例如:自动离场、加速、巡航、制动等.ATS系统与地面控制器一起提供了基于当前运行状况的速度保护线,而ATP系统使用该保护线来限制ATO系统.因此,ATO系统与其他两个子系统一起工作,并在ATS系统与牵引或制动控制设备之间建立连接.具体来说,ATO系统的定速控制负责在不同的负载和运行条件下将列车的速度控制到目标值.在铁路条件发生变化时,控制策略要求能够快速适应不断变化的环境.

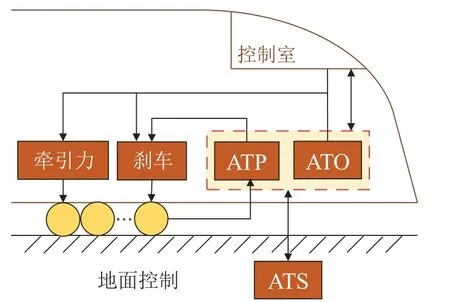
图1 自动列车控制系统Fig.1 ATS system

2.2 定速控制问题

ATO系统的动力学模型可以抽象如下:

其中:u表示控制输入量,ξ表示外部干扰,χ表示ATO系统的状态变量,n表示环境标签,N为标签数量.然而,精确的动力学模型通常难以获得,并且列车运行期间环境会发生变化,增加了为ATO系统构建自适应控制器的难度.

通常,整条铁路可以被分成许多段,每一段的列车路况条件基本相同.例如,铁路坡度在列车一段沿线内保持恒定.因此,本文可以为控制器收集足够的样本以适应不断变化的操作环境,得到一种数据驱动的自适应控制器.

2.3 本文的目标

这项工作的目的是设计一种无模型的元强化学习算法用于解决列车定速控制问题.该算法能学习一个自适应控制器,其能够在短时间内适应变化的环境.Meta-RL框架解决定速控制问题的优势至少包括:1)在实践中很难获得ATO系统的精确动力学模型,而本文的算法不需要动力学模型;2)作者将模型的不确定性和外部干扰视为环境的组成部分,因此减弱了他们的影响;3)Meta-RL学习的是自适应控制器,该控制器可以在短时间内适应变化的铁路环境.

3 定速控制的MDP

在本节中,作者将列车定速控制问题建模为未知转移概率的一系列平稳MDP问题.

3.1 马尔可夫过程

马尔可夫性表示智能体的当前状态包含所有相关信息.满足马尔可夫性的强化学习任务称为MDP.MDP 通过其4个组成部分来描述: 1)状态空间S;2)动作空间A;3) 损失函数c(s,a):S×A →R;4)转移概率p(sk|s1,a1,...,sk-1,ak-1).马尔可夫性可确保当前状态仅取决于最后一个状态和动作,即

MDP描述了智能体与环境交互的过程: 智能体在当前状态下sk采取行动ak,然后和状态转移到了sk+1,同时,返回损失函数ckc(sk,ak),如图2所示.

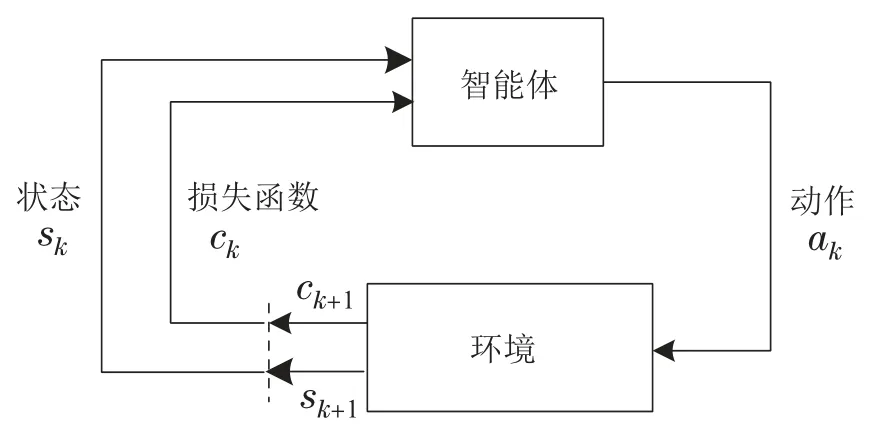
图2 马尔可夫过程[15]Fig.2 MDP[15]

策略是从状态空间S到动作空间A的映射,即π:S →A.RL的目的是找到可以最小化长期累积损失的最优策略π,即

其中:P是策略空间,ck是单步损失,0＜γ ＜1是折扣因子,用于衡量损失函数随时间的衰减,H表示时间窗长度.

为将列车的定速控制问题建模为MDP问题,需要合理定义MDP的4个元素.显然,MDP的动作应当被定义为ATO系统的控制输入.因为真实的动力学模型难以获得,假设MDP的转移概率未知.因此,本文主要专注于设计MDP的状态和损失函数.

3.2 MDP的设计

定速控制问题的目的是以最小的能量消耗将列车的速度控制到目标速度vref.因此,损失函数可以定义如下,其中vk-vref表示速度误差,驱动力力u(k)衡量能量消耗.损失函数通过系数在两个控制目标之间进行权衡.第k步的损失函数定义如下:

这里ρi,i {1,2}是正的常数,vref指参考速度.

状态设计的基本原则是状态应能够充分地表达系统.本文参考现有文献中的动力学模型[2],将MDP的状态设计为

定义好状态和损失函数后,可以用RL求解MDP问题.一般而言,RL仅适用于平稳MDP,即MDP的单步转移概率是时不变的.由于列车运行期间环境的变化,实际情况并非如此.例如,山区的铁路坡度和平均风速不同于平地的铁路坡度和风速,这导致了ATO系统动力学模型的变化.为此,本文将整个铁路划分为N个分段,以使每个分段内的线路条件几乎相同,对应于一个平稳的MDP,其转移概率为pn(sk|sk-1,ak-1)1,2,...,N},如图3所示.因此,本文将变化环境下的定速控制问题建模为一系列平稳的MDP,进而由Meta-RL框架解决.

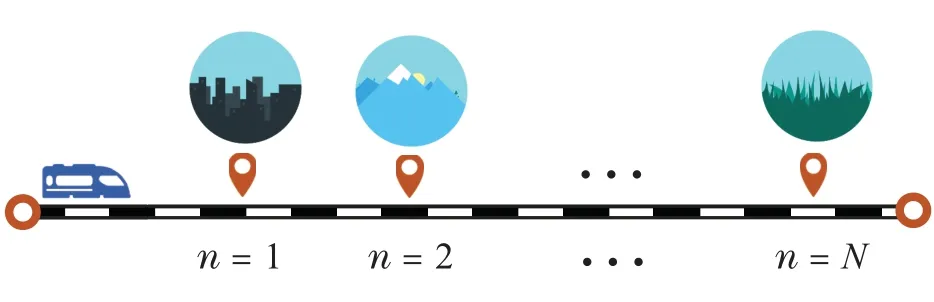
图3 整个铁路分为N段并且在每个段中铁路路况均相同Fig.3 The railway is divided into N segments

4 基于Meta-RL求解定速控制问题

在本节中,本文介绍了元学习问题,并提出了用于列车定速控制的Meta-RL方法.

4.1 元学习

元强化学习的目标是学习一个可以快速适应新任务的策略.为此,该策略在元学习阶段针对一组学习任务进行了训练,使新任务的损失函数相对于策略参数的敏感度最大化.

考虑参数化策略π(a|s,θ),参数为θ.在元学习过程中,对策略进行训练,使其能够适应大量任务.任务被定义为

其中1,2,...,N},包含损失函数

初始状态分布qi(s1),转移概率pi(sk+1|sk,ak),时间窗长度H.此处,损失函数LTi定义为采样轨迹上的累积损失

RL任务Ti对应于一个转移概率pi(sk+1|sk,ak)不变的平稳MDP.在元学习框架中,作者希望初始策略能够自适应从分布p(T)中采样的任务.因此,训练过程中,作者从p(T)中采样任务p(Ti),然后将策略用于与此任务相对应的MDP,获得MDP的K条轨迹.进而,根据这些轨迹用RL对策略进行评估,用梯度下降法单步更新策略.对更新后的策略再次评估,得到的测试误差用来训练初始策略参数.实际上,元学习建立了初始策略的内核表示形式,该策略广泛适用于许多任务.

对于列车定速控制问题,将整个铁路划分为N个分段,并且每个分段内的运行条件都认为是相同的,对应于一个平稳MDP.因此,可以将整个铁路列车的定速控制问题表述为一系列RL任务.元学习通过从这些任务中随机采样以学习初始策略,并将整个任务作为训练集.当列车在铁路的新分段i上运行时在线收集样本以计算损失LTi,作为对适应的反馈初始策略.

4.2 元强化学习

Meta-RL旨在通过元学习来学习初始策略,以便可以仅使用少量训练样本来解决新任务.这种方法背后的想法是,某些内部表示形式比其他内部表示形式更具可移植性,因此它们广泛适用于p(Ti)中的所有任务,而不是单个任务[13].本文旨在学习一种策略,其参数的微小变化将大大改善从p(Ti)采样的任务的损失函数.本文将基于梯度的学习用于此元学习过程,如图4中所示.当适应到新任务Ti时,策略参数θ变为.更新后的参数通过一步梯度下降得到

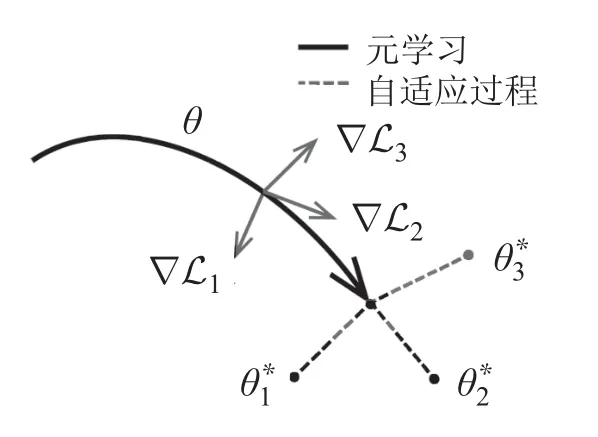
图4 元学习算法的示意图Fig.4 An illustration for meta learning

其中步长α为衰减步长或为常数.初始策略参数θ通过优化自适应后的策略π()所对应损失函数得到.该损失函数从分布p(T)采样出的任务中可以计算出来.具体来说,元学习的目标是

元学习通过优化初始策略参数,以使在新任务上仅一步梯度下降即可在该任务上产生最好的效果.可以通过以下随机梯度下降对初始策略参数进行更新

这里β是元学习的步长.

对于定速控制问题,元学习要求列车在整条铁路上运行以收集样本轨迹.在第i个分段中,智能体可以从初始策略θ进行自适应θ-α∇θLTi(θ),并在同一段上测试调整后的策略,以获取用于元学习的样本.同时,使用每个分段的所有采样轨迹来完成元学习,即学习初始策略.

但是,对于自适应阶段(3)和元学习阶段(5)很难计算损失函数的梯度,因此本文利用策略梯度法来通过样本近似梯度.

4.3 梯度的计算

长期累积损失函数取决于动作的选择和状态的分布,因此很难针对θ写出显式表达式.幸运的是,策略梯度定理[16]为本文提供了不涉及状态分布µ导数的L(θ)梯度的解析表达式

这里分布µ是策略π下的分布,qπ(s,a)是从状态s执行a之后的损失函数.随机梯度通过下式计算这里Gk是长期损失.这种更新规则基于一种蒙特拉洛算法REINFORCE[17],要求基于当前策略的一段完整的轨迹{s1,a1,...,sH,aH}.

元学习(5)使用信赖域策略优化法(TRPO)[18]更新.为节省空间,这里本文省略了TRPO的介绍.

综上所述,本文提出了一种基于梯度的Meta-RL算法用于ATO系统的定速控制.通过求解一系列MDP,作者在变化的铁路条件下对列车的定速控制问题进行了建模.元强化学习能学习一个初始策略,该策略可以通过使用少量样本来适应新的MDP,而无需手动重置其参数.

5 算法的应用

本节讨论元强化学习算法应用到定速控制上的实现细节.算法的仿真主要包含5个部分:仿真器、初始化、数据收集、神经网络的结构以及训练.

1) 本文的强化学习控制器不要求系统动力学模型已知,但是需要一个仿真器以产生列车的系统输入输入数据(s,a,s＇,c).同时,元学习要求已知任务的分布.这在列车定速控制中是很容易实现的.例如,假设铁路的斜率在区间内变化,将分布设置为该区间内的均匀分布即可.

2) 初始化主要涉及策略神经网络的初始化.一般的强化学习算法还设计经验池的初始化.经验池可以是空的,或是存放从以往训练中保留下来的数据.

3) 算法每次在一个任务中采样前都会把状态设置为某个初始状态.样本会不断收集并加入经验池,以估计当前任务中参数的梯度.在元学习阶段,算法会从任务分布中随机挑选任务进行数据收集.

4) 在列车控制问题中,策略网络设计为有两个隐藏层的单输入神经元网络,每层有30个神经元,ReLU函数用作激活函数.由于实际中动车组的最大牵引力约为300 kN,本文需要对策略网络的输出幅值进行限制.为此,将输出层设置为tanh函数.ReLU函数和tanh函数的示意图如图5所示.神经网络示意图如图6所示.

图5 左图为ReLU函数,右图为tanh函数Fig.5 The left picture is ReLU function,and the right one is tahn function

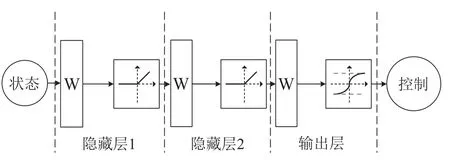
图6 策略网络的结构Fig.6 Structure of the policy network

5) 策略网络的训练是算法的核心.元学习阶段评估参数在经过单步梯度下降之后的平均性能,据此进行改进.参数的单步梯度下降可以通过一般的强化学习算法完成,本文中选择的是TRPO算法.

注意,训练任务的数量N的大小对控制器的性能没有明显相关性.N增大,要学习的任务增多,故总样本数量增大,训练时间更长,影响的是元学习阶段所得初始策略的性能.但是,N增大后单步梯度下降的步长也相应改变,因此自适应后所得策略性能不会有明显变化.

6 仿真

在本节中,本文将通过仿真来验证Meta-RL算法的性能.作者首先描述了仿真用的自动列车控制模型,然后通过元强化学习学习得到自适应反馈控制器.最后,作者与线性二次控制器的结果进行了对比,验证了自适应控制器可以迅速适应铁路的新路况.

6.1 ATO动力学模型

本文考虑一个经典的ATO模型[2]用于验证作者的算法.请注意,此模型仅用于生成样本以训练策略网络.系统动力学方程为

这里co,cv和ca是系数,p代表外界扰动,u是整辆列车的驱动力.假设作者把整个铁路分为N段,φn,n {1,2,...,N}表示每一段上的铁路坡度.但是,式(6)中的参数无法准确获得,且由于未知原因(例如,线路条件和列车质量)会在一定范围内变化.动车组的最大牵引力约为300 kN.模型系数的值在表1中列出.

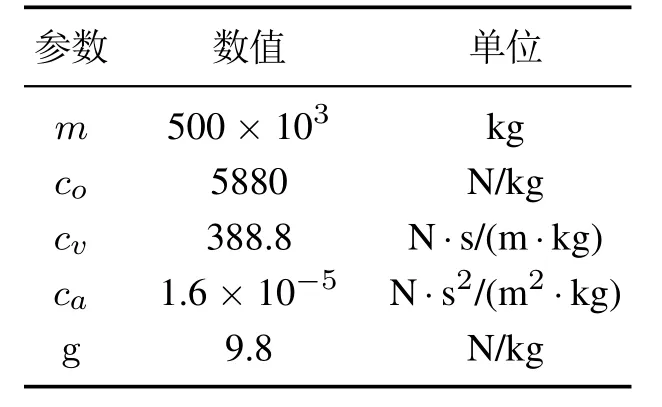
表1 动力学参数Table 1 Dynamic parameters

6.2 仿真设置

Meta-RL算法在Linux系统中使用Python 3.6实现.注意,仿真环境需要实现为离散时间模型.为此,使用前向Euler公式离散化ATO系统的动力学模型.

在此,MDP的4个部分分别设计为:1)状态skvk-vref;2)动作为牵引力uk;3)损失函数为c(sk,uk)ρ1(vk -vref)2+ρ2u(k)2;4)转移概率由列车动力学模型(6)表示.在仿真中本文将轨道斜率作为环境标签n,即动力学模型(6)随着轨道斜率φn,n {1,2,...,N}而改变.离散系统的采样时间为dt0.1 s.参数的扰动范围设置为表1中数值的5%,同时允许外界扰动有5%的波动.由于动车组的牵引力被限制为300 kN,本文设置轨道斜率从-2°到2°均匀变化,即任务分布p(T)为均匀分布.元强化学习算法设置如下.元学习的步长β0.1,自适应梯度更新的步长为α0.5,每一个片段的长度设置为H1000,用于训练的任务个数为30个.元学习阶段共进行600次,即随机采样600次任务进行元训练.自适应阶段采集样本的时间窗长度设置为30步,采样10条轨迹.

6.3 仿真结果

列车定速控制问题的仿真结果如图7和图8所示.经过600个训练步,本文获得了策略的初始参数.然后,从p(T)中随机选择一个任务,对应于铁路坡度φn,并使用初始策略来控制列车fn(χk,uk,ξ).红色虚线表示在Meta-RL学习的初始策略下获得的速度轨迹.速度确实会很快收敛,但不会收敛到参考速度.这个结果是合理的,因为训练的初始策略在遇到新任务时需要一些样本以进行调整.为了收集这些样本,列车在选定的铁路坡度下遵循初始策略运行.在将列车从40 m/s减速到20 m/s的实验中(图7),本文设置了采样轨迹的数量K10和采样时间窗长度H30,即适应时间为30 s,与整个运行周期相比,这是合理的.请注意,对于定速控制而言,初始策略下的这些采样轨迹几乎是相同的,这意味着能生成多个轨迹并将其复制以进行梯度计算,进一步减少采样时间.蓝线表明,按照调整后的策略,速度会迅速收敛到目标值,而不会出现过冲.作者可以观察到速度一直在微弱地振荡,这是由于策略是由神经网络近似的.这两个策略下的控制输入轨迹如图7和图8所示.注意到由于输出层为tanh函数,神经网络的控制输出很好地满足了300 kN的限幅条件.

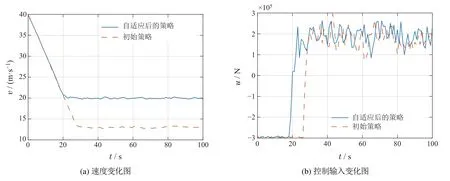
图7 在初始策略以及自适应后的策略控制下的输入及速度轨迹Fig.7 The trajectories of input and velocity under the initial policy and adapted policy

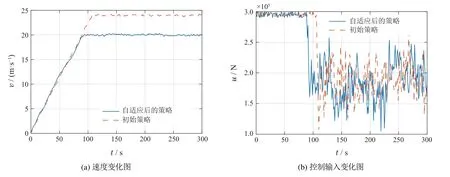
图8 在初始策略以及自适应后的策略控制下的输入及速度轨迹Fig.8 The trajectories of input and velocity under the initial policy and adapted policy

由于元强化学习基于最优控制框架,接下来,本文对列车进行了基于模型的线性二次控制(LQR)作为对比.为此,将式(6)在v0处近似为线性模型

在这里,令A1-dt.cv/m,B-dt/m,wkdt((co+p)/m-gsinφn).由于线性二次控制无法估计当前路况的斜率φn,令φn0.LQR控制器由下式给出

其中

l满足vrefAvref+B(-Kvref+l)+dt.co/m以抵消外界噪声的影响.设置Q1,R10-11.注意LQR控制器要求模型信息完全已知.为了满足最大驱动力的限制,本文将其控制输入限制在300 kN以内.

LQR控制器的效果如图9所示.可以看出,在两条速度控制曲线中都存在明显的静差,即速度不能完全跟踪参考速度.这是因为LQR无法获得当前的路况信息,所以无法对轨道斜率带来的误差进行补偿.而且,LQR系统要求模型完全已知,这在实际中是很难满足的.作为对比,本文提出的元强化学习控制器则不需要已知任何动力学模型参数.

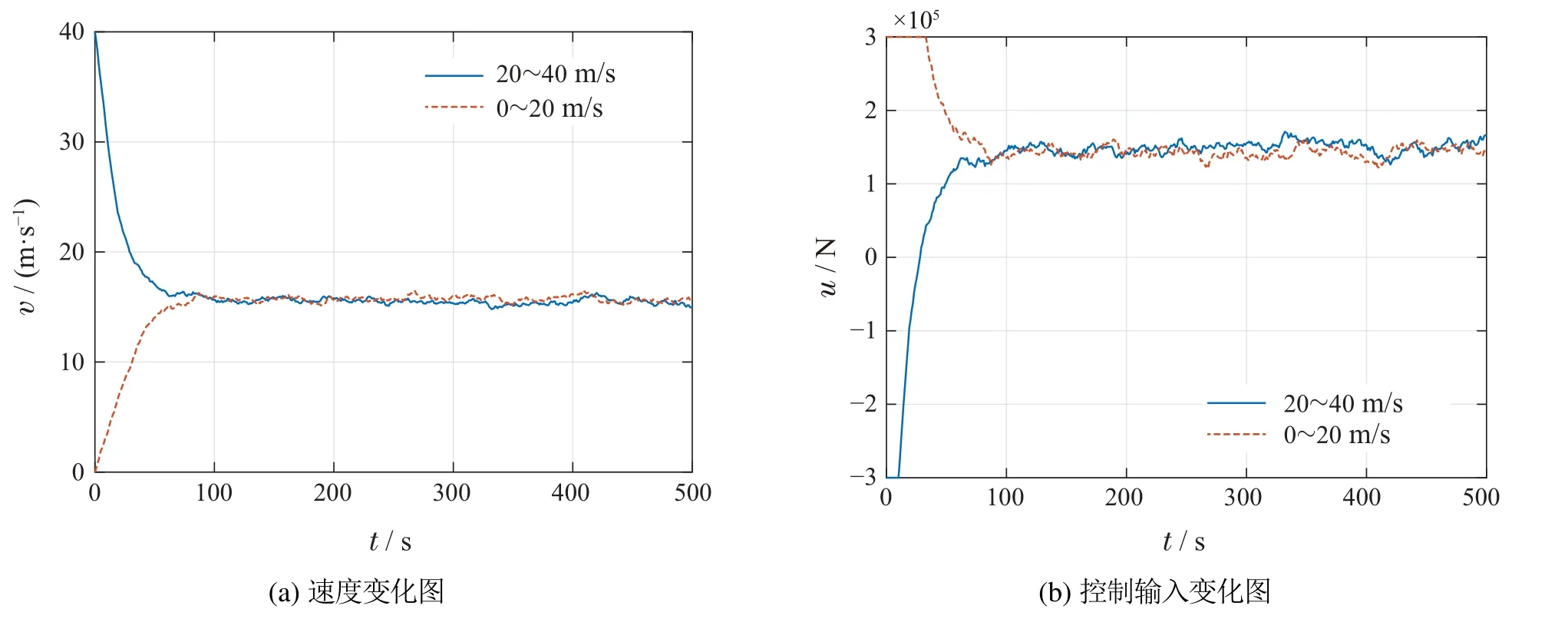
图9 应用LQR后的控制效果Fig.9 The trajectories of input and velocity under LQR

为了展示元强化学习控制器的自适应性能,测试列车以恒定速度要求经过不同区段时的速度保持情况.仿真时间设定为300 s,自适应时间为20 s,列车参考速度为10 m/s,在0～100 s,100～200 s及200～300 s区间内的轨道斜率分别为0,1°以及2°.同时,模拟列车的真实运行情况,对系统矩阵A引入5%的标准高斯随机噪声以及外界扰动.元强化学习控制器下的速度变化曲线如图10所示.可以看出列车在有扰动以及参数噪声的情况下开始时仍能快速控制到参考速度.在100 s以及200 s时刻进入自适应阶段收集数据,速度由于轨道斜率突变出现小幅度偏离,20 s后自适应控制器即将速度调节到参考速度.最后,本文画出了不同区间下列车的变速控制曲线,即在0～100 s,100～200 s及200～300 s区间内的参考速度分别为10 m/s,20 m/s以及5 m/s,控制效果如图11所示.同样的,除了在轨道斜率突变的自适应阶段速度控制受到影响外,列车均可被很好地控制到参考速度.

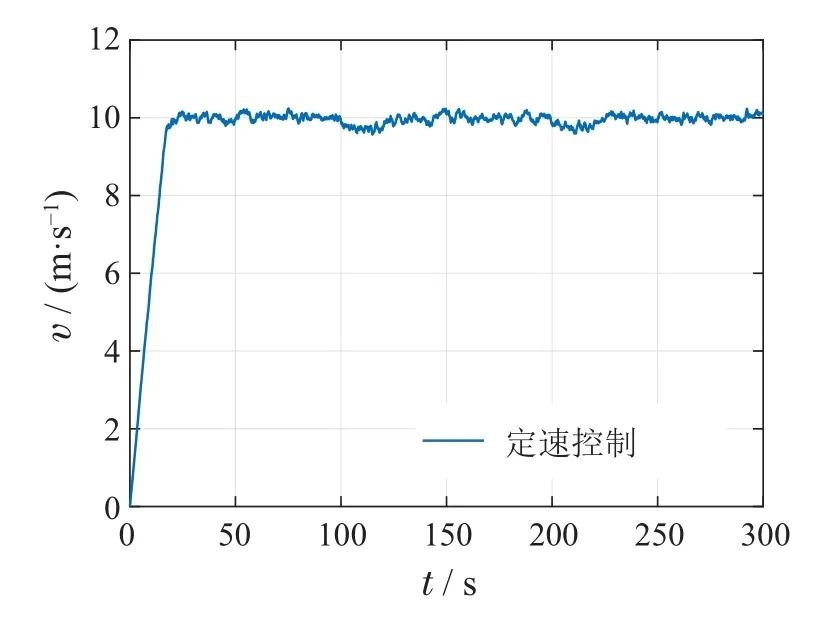
图10 不同斜率区间下的定速控制Fig.10 Velocity regulation under multiple railway segments

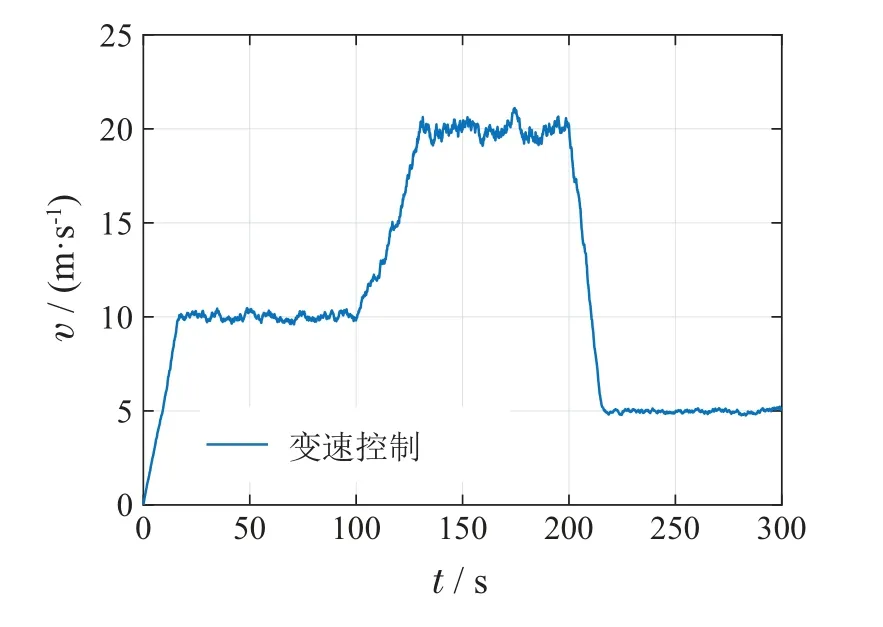
图11 不同斜率区间下的变速控制Fig.11 Velocity tracking under multiple railway segments

7 结论

本文提出了一种无模型的元强化学习控制框架,用于在变化的铁路运行条件下控制列车自动运行的速度.为此,作者将定速控制问题建模为一系列转移概率未知的平稳马尔可夫决策过程MDP.在元学习框架下,本文提出了一种无模型的定速控制方法,能学习一种自适应控制器,其在变化的环境下将列车的定速控制到目标值.仿真验证了元强化学习的自适应控制器的性能.

比定速控制问题更一般的情况是自动列车运行的速度跟踪问题,其要求在时变铁路条件下跟踪速度轨迹.这将是未来的工作.