固定时间预测器下的欠驱动无人艇路径跟踪控制

王山丹,孙梦薇,刘 剑,孙长银

(1.东南大学自动化学院,江苏南京 210096;2.安徽大学物质科学与信息技术研究院,安徽合肥 230039)

1 引言

21世纪是海洋的世纪.海洋中丰富的矿物资源和渔业资源不仅能提供巨大的经济价值,而且海洋环境作为国家领土的重要组成部分,是国家主权行使的地理空间之一,也是关乎国家安全的国防屏障.因此,为合理开发海洋资源,提高海洋军事作战能力,维持国家领海地区和平稳定,对海洋无人装备进行分析研究尤为重要._________

无人艇是一类能在水面自主移动,实现海上作业的智能船艇,具有无人自主、成本较低、可在危险场景下作业等特点.通过搭载不同的传感器,其可实现自主导航定位、路径跟踪、目标探测、环境感知等功能.在民用领域,水面无人艇不仅可应用于捕捞、搜救、测量、环境监测等方面.而且在军用领域,水面无人艇也能应用于自主巡逻、信息通讯、扫雷、水面防卫等方面[1-2].

高精度的路径跟踪使无人艇在指定时间自主航行到指定地点是无人艇完成上述作业的基础.无人艇作为一类典型的欠驱动系统,由尾部螺旋桨产生的纵向推力和方向舵产生的转舵力矩控制其在水平面和艏向角3个自由度上的运动,且其在各个方向上的运动存在耦合.在给定路线的情况下,如何控制无人艇螺旋桨和方向舵,使无人艇精确的沿着规定路径前进,已成为当下的研究热点[3].

无人艇的路径跟踪常采用导航律与控制律分离的结构独立设计[4].在导航律部分计算期望偏航角使无人艇的跟踪位置误差收敛到零,再设计控制器控制转舵力矩使无人艇能精确跟踪期望偏航角,始终沿期望路径前进.常用的控制方法有非线性制导法[5-7]、向量场法[8-9]、视线法(line-of-sight,LOS)[10-13]等.视线法将船艇头部的朝向与期望路径的交点作为参考目标点,通过调整艏向角使其精确的沿着目标路径运动.由于视线法设计相对简单,使用方便,已被广泛应用于无人艇的路径跟踪[10,15-16].文献[17]首先提出将基于视线法的制导律用于欠驱动无人艇路径跟踪,并利用反步法设计非线性控制器,证明所提出的导航方法和控制系统的有效性.文献[11]进一步在存在较小环境扰动的情况下利用视线法实现了对由直线和圆弧组成的杜宾斯路径的路径跟踪,该方法认为无人艇侧滑角小于5°,近似为常数.文献[18]针对环境扰动较大的情况提出了一种基于预测器的导航律(predictorbased line-of-sight,PLOS),通过预测跟踪误差估计未知侧滑角,对环境扰动进行补偿,从而使导航更准确,减少震荡.文献[4]在此基础上提出一种能在有限时间收敛的预测器,能使预测误差更快收敛到零,还利用径向基神经网络(radial basis function neural network,RBFNN)对无人艇模型进行训练,减少模型不确定性,解决了由洋流等因素引起的大测滑角的问题,提高了跟踪稳定性.

基于以上分析,本文在传统视线法制导的基础上,首次提出了一种新的基于固定时间预测器的制导方法,并证明了闭环系统的稳定性.据笔者所知,目前还没有人做过基于固定时间预测器制导律的相关内容.考虑到实际海洋环境中存在外部环境干扰及不确定,本文采用固定时间预测器对跟踪位置误差进行预测,在线估计外部干扰产生的侧滑角,保证预测器误差在固定时间收敛到零,且收敛时间上界与系统初始状态无关,实现对侧滑角的补偿.在所提出的固定时间制导律的基础上,为了保证跟踪控制的有效收敛,本文进一步设计了固定时间收敛的控制器,使无人艇艏向角在固定时间收敛到期望艏向角,以满足导航律的要求.该方法设计简单、计算量小、且收敛速度快,收敛时间不依赖于初始值.最后,通过几组仿真实验,验证了本文所设计的制导律和控制器的有效性.

2 问题描述

2.1 数学模型

无人艇的固定时间路径跟踪问题是基于其运动学和动力学模型,研究如何设计控制输入,使跟踪误差在固定时间收敛到零.为了跟踪给定路径,首先设计导航律,根据跟踪误差在固定时间收敛到零计算出期望艏向角,将路径跟踪问题转化成艏向角跟踪问题,再设计控制器控制转舵力矩,使无人艇的艏向角在固定时间收敛到期望值.

本文研究的欠驱动无人艇有2个控制器,分别是船尾部的推进器控制船向前运动和船舵用来控制船的航向,使船在3个自由度上运动.无人艇在3个自由度上的运动在大地坐标系{E}下可以表示为[11]

其中:x,y表示无人艇的位置,u,v分别表示船的纵荡和横荡速度,ψ和r分别表示船的艏向角和角速度.

忽略模型摄动和环境干扰力等不确定性的影响,无人艇在水平面运动的动力学模型可以表示为[19-20]

其中:Fu为螺旋桨推力,Tr为方向舵力矩,m11,m22,m33分别表示船的惯性矩阵在船体坐标系3个坐标轴上的分量,Xu,Yv,Nr和X|u|u,Y|v|v,N|r|r分别为一阶阻尼和二阶阻尼系数.

2.2 跟踪误差模型

为实现无人艇的路径跟踪,在船的期望路径上定义一个坐标为(xp(θ),yp(θ))的虚拟船,视作跟踪目标,所以沿期望路径切向和法向方向上的跟踪误差可以表示为

其中γparctan为虚拟船在期望路径上的航向角.

对式(3)求导可得

其中upcosγp+sinγp为虚拟船沿期望路径的运动速度.

将式(1)代入式(4)-(5)中得到

其中:U为无人艇的运动速度,βarctan(v/u)为侧滑角.侧滑角通常由风浪等外部扰动造成,且随时间缓慢变化,可认为≈0.且侧滑角非常小,可近似认为cosβ≈1,sinβ≈β[11].

整理可将式(6)-(7)的无人艇运动学跟踪误差模型改写为

3 导航律

3.1 关于侧滑角的固定时间预测器

引理1[21]对于系统f(x),若存在连续可微函数V(x),正实数µ1,µ2,(0,1),(1,+∞)使

引理2[14,23]对于连续可微函数V(x),存在正实数µ1,µ2(0,∞),(0,1),(1,∞)使

其中θ是一个标量并且满足0＜θ ＜1,收敛时间T满足

引理3[2,25]假设x1,x2≥0,0＜p≤1,q ＞1,则有

定义1[22]如果系统的原点是Lyapunov稳定的,并且存在一个设定时间T≥0,在t≥T时,使得任意的解能够收敛到平衡点的一个充分小的邻域内,那么称系统的原点是实际固定时间稳定的.此外,存在一个正常数Tmax使得T≤Tmax对于任意的初始状态都是成立的.

在没有外界扰动的情况下,无人艇的推进力仅由尾部推进器提供,因此无人艇艏向即为实际运动的方向.传统的视线法制导律根据无人艇实际位置和期望路径计算期望艏向角,通过控制无人艇转向舵,使其在期望艏向角下朝期望路径上的虚拟目标点移动.但由于风浪等环境扰动,无人艇不仅受推进力的作用,还受到来自其他方向的扰动力,使无人艇艏向和实际航向之间产生一个夹角,这个角被称为侧滑角.侧滑角的存在使得无人艇实际艏向角难以追踪期望航向,无法精确跟踪给定路径.为了获取环境扰动造成的未知侧滑角,对其进行补偿,基于文献[4]的研究成果,本文设计了式(17)-(18)所示的固定时间位置误差预测器.

其中C为待设计的正常数.

为证明在式(20)-(22)所设计预测器下,系统固定时间稳定,设计李雅普诺夫函数如下所示:

对式(23)求导可得

3.2 导航律设计

视线法是一类非线性路径跟踪方法,目前已被广泛用于欠驱动无人艇的跟踪控制[10-12].它的主要思想是模仿舵手的行为,以无人艇头部朝向与期望路径的交点作为参考目标点,并不断调整航向达到参考目标点.其基本原理是设计无人艇期望艏向角,使无人艇的位置误差收敛到零,从而精确地跟踪给定路径.将无人艇的期望艏向角定义为[11]

其中:Δ为前视距离,γp可由期望路径求得.

将期望路径上虚拟船的速度定义为

虚拟船速度up可以作为虚拟控制输入来稳定无人艇的跟踪误差,ku为正常数参数.

为证明在期望艏向角下,无人艇的位置误差能收敛到零,精确跟踪期望路径,选取李雅普诺夫能量函数

由式(26)可得

由式(26)(29)-(30)可得

对式(28)求导,并将式(31)-(32)代入得到

将式(34)代入式(33)得

令

在第3.1节中已证明,存在T,当t ＞T时,()能收敛到原点附近充分小的邻域内.因此,t ＞T时,在式(26)所示的艏向角下,系统(20)-(21)一致渐近稳定,所预测的无人艇到期望路径上虚拟点的位置误差能收敛到原点.

4 控制器设计

4.1 控制目标

在导航律设计中,对于给定的期望跟踪路径,已根据预测跟踪误差和预测侧滑角计算出期望艏向角,使无人艇在期望艏向角下到给定路径的位置误差收敛到零.但由于艏向角不能被直接控制,本节将根据无人艇动力学模型(2),设计控制船舵转向的力矩Tr作为控制器,控制无人艇艏向角.为保证控制器的有效收敛,控制器的设计分为两步.首先设计期望艏摇角速度,保证在期望艏摇角速度下,无人艇艏向角误差能固定时间收敛到零,再根据无人艇动力学模型,利用期望艏摇角速度计算出所需要的转向力矩,从而实现固定时间收敛的控制器设计.

4.2 航向跟踪控制器设计

为跟踪艏向角,设计期望艏摇角速度为

将艏向角跟踪误差定义为

为证明在式(36)所示的艏摇角速度下,无人艇艏向角误差能在固定时间收敛到零,构造关于艏向角误差的李雅普诺夫函数如下:

对式(38)求导得

将式(36)代入式(39)可以改写为

由引理1,该系统是固定时间稳定的,即通过设计如式(36)所示的虚拟控制输入rd,艏向角误差ψe可以在固定时间收敛到原点.下面将根据无人艇运动学模型和虚拟控制输入rd计算出转向控制力矩Tr.

将无人艇艏摇角速度和跟踪速度误差定义为

根据动力学模型设计欠驱动无人艇控制船舵的转向力矩Tr为

为证明在式(43)的控制输入下,无人艇的艏摇角速度和跟踪误差可以收敛到零点,可设计如下的李雅普诺夫方程:

将式(43)代入式(2)有

对式(44)求导,并将式(45)代入

由引理2可知,该系统是固定时间稳定的,因此,通过设计如(43)所示的控制力矩,无人艇艏摇角速度跟踪误差可以在固定时间收敛到零,艏向角跟踪误差也在固定时间收敛到零,能有效跟踪第3节导航律所设计的期望艏向角.相较于反步法和设计滑模面的控制方法,本文所设计的固定时间收敛的控制器能更快跟踪期望艏向角,且收敛时间上界不依赖于艏向角初始值.

5 仿真实验与分析

5.1 直线路径跟踪

本文选取的无人艇动力学模型参数如表1所示[20],且m11215 kg,m22265 kg,m3380 kg.m2.首先,利用本文提出的基于固定时间预测器的无人艇路径跟踪方法对直线路径进行跟踪.选取待跟踪路径xθ,yθ,无人艇初始位置和姿态角(x,y,φ)(-10,10,0),初始速度和转向角速度(u,v,r)(0,0,0),选取的控制器仿真参数k10.7,k20.5,k30.7,k40.5,k50.7,k60.5,ku3,kx10.5,kx20.2,ky10.4,ky20.1,m3/7,n7/5,C0.8,δ5.

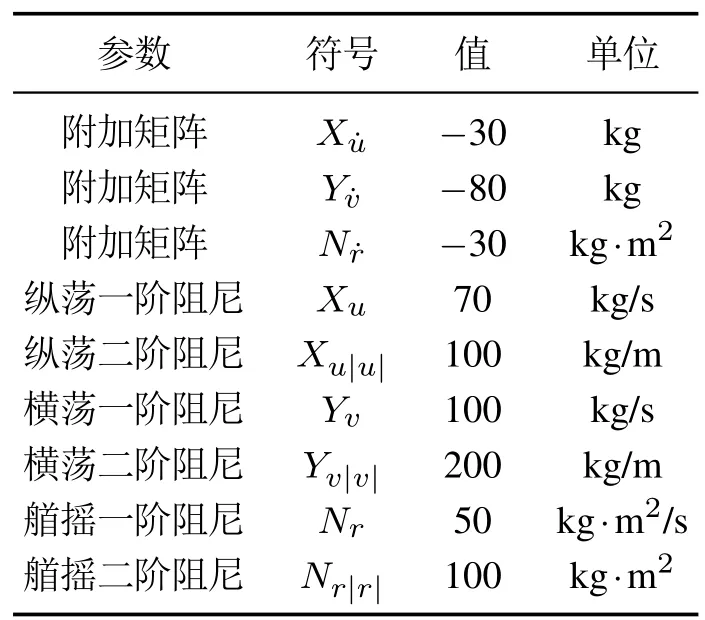
表1 无人艇动力学模型参数Table 1 Dynamic parameters of the USV

图1-3给出了在本文提出的控制方法下无人艇沿直线路径运动的位姿变换情况,证明利用本文所设计的控制器,无人艇能精确的跟踪给定直线路径,且曲线平滑,误差渐近收敛.

图1 USV跟踪直线路径效果图Fig.1 Path following performance of straight line

图1给出了USV跟踪直线路径的效果图,图2为无人艇实际偏航角和期望艏向角随时间变化情况,图3为横向和纵向两个方向上的跟踪误差随时间变化情况,由图可以看出本文所设计的固定时间收敛的控制器能使无人艇很好的跟踪期望艏向角,且无人艇在x轴和y轴两个方向上的位置误差分量能收敛到零.

图2 USV偏航角跟踪表现Fig.2 The reference heading and the actual heading angle

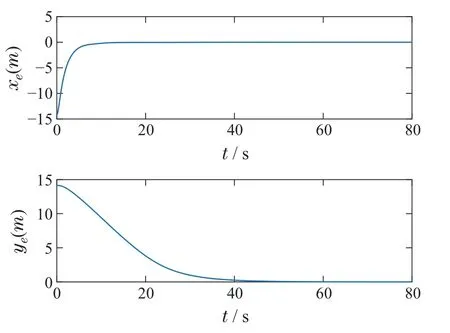
图3 USV路径跟踪误差Fig.3 Along-tracking error and cross-tracking error

将本文提出的固定时间预测器对跟踪误差的预测误差与有限时间预测器的预测误差进行对比,选取预测器参数k10.5,k20.5,m3/7,n7/5,根据引理2,在δ0.9时,可以得到Tmax20.5 s.在不同初始条件下预测器预测误差的仿真结果如图4-5所示.

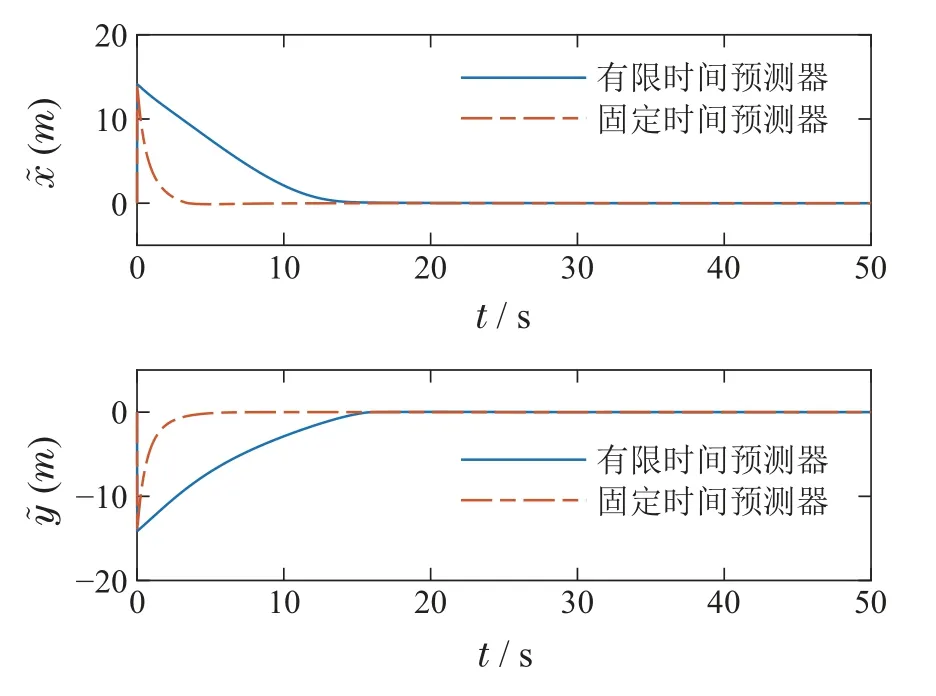
图4 预测器预测误差(无人艇初始位置为(-10,10))Fig.4 The predictor error(initial position of USV(-10,10))

图4为无人艇初始位置在(-10,10)的预测器预测预测误差,图5为无人艇初始位置在(-50,50)的预测器预测预测误差,初始偏航角均为设0.进一步选取不同的控制参数m,n,和控制增益参数k1,k2,分析固定时间预测器的收敛时间与控制参数的关系,在无人艇初始位置为(-10,10)时预测器预测误差与时间的变化关系如图6-7所示.

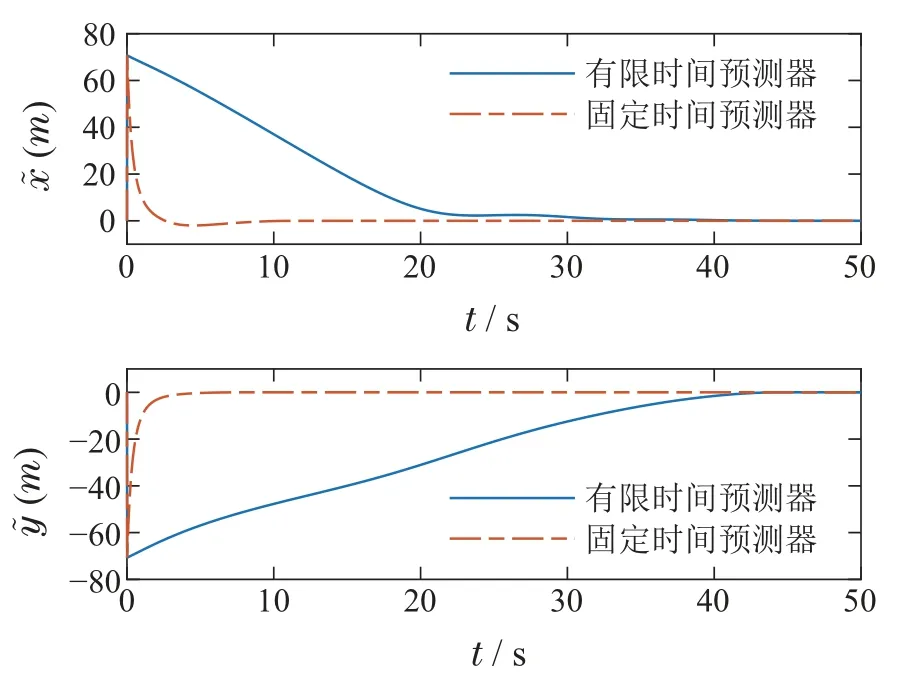
图5 预测器预测误差(无人艇初始位置为(-50,50))Fig.5 The predictor error(initial position of USV(-50,50))

图6 不同控制参数m,n下预测器预测误差Fig.6 The predictor error with different control parameters

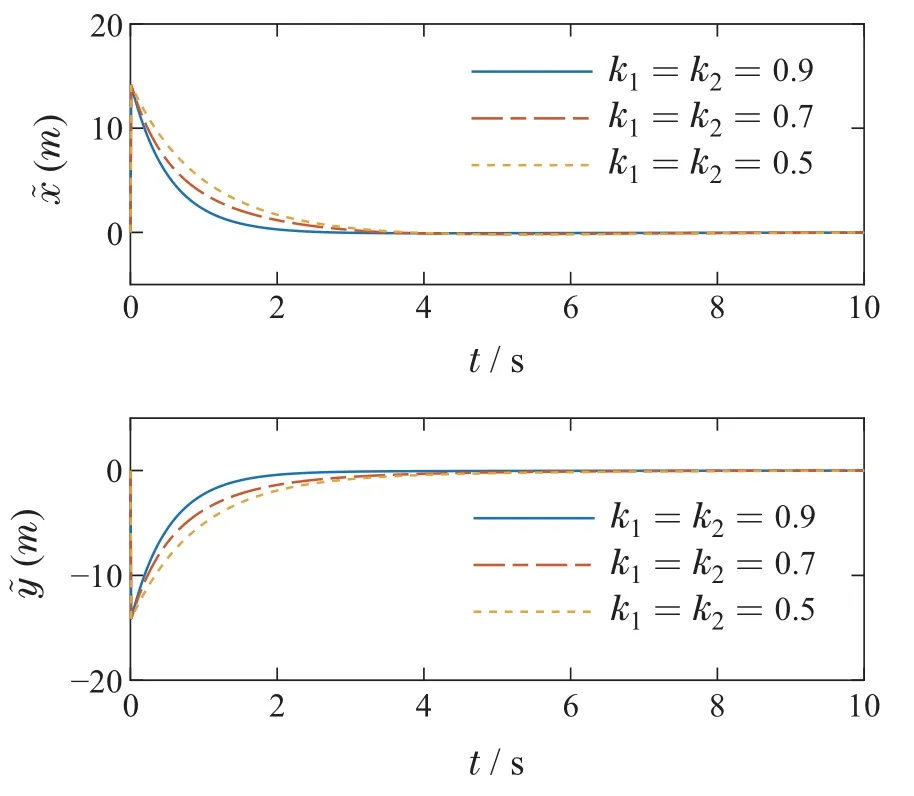
图7 不同控制增益参数k1,k2下预测器预测误差Fig.7 The predictor error with different gain parameters

仿真结果表明,当选取的控制参数m越小n越大时,预测器收敛时间越小.当选取的控制增益参数k1,k2越大时,预测器收敛时间也越小.对比图4和图5可以看出预测误差在3 s时已经收敛到零,满足T≤Tmax,且本文提出的基于固定时间预测器相比于有限时间预测器,预测误差收敛时间与误差初始值无关,能更快收敛,预测性能更好.

5.2 曲线路径跟踪

第2组仿真实验将期望路径设置为曲线,无人艇初始位置和姿态角为(x,y,φ)(-5,8,0),初始速度和转向角速度为(u,v,r)(0,0,0),期望路径曲线设计为x(θ)1.5θ,y(θ)10+1.5 sin(0.1θ).无人艇在固定时间预测器和有限时间预测器的制导律下对曲线路径的跟踪效果如图8所示,跟踪误差如图9所示,期望偏航角与真实偏航角随时间的变化关系如图10所示.

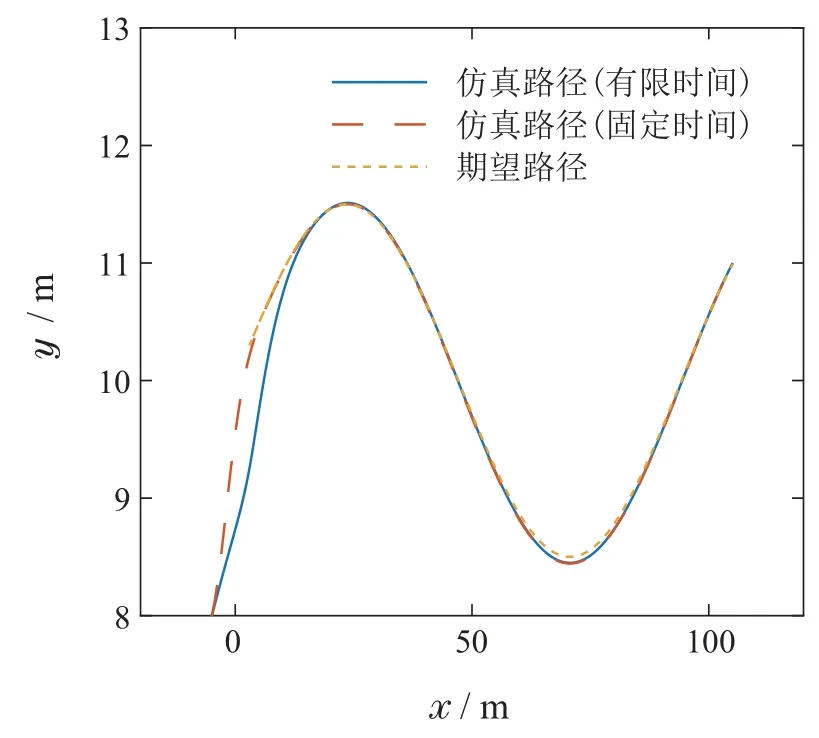
图8 USV跟踪曲线路径效果图Fig.8 Path following performance of curved path

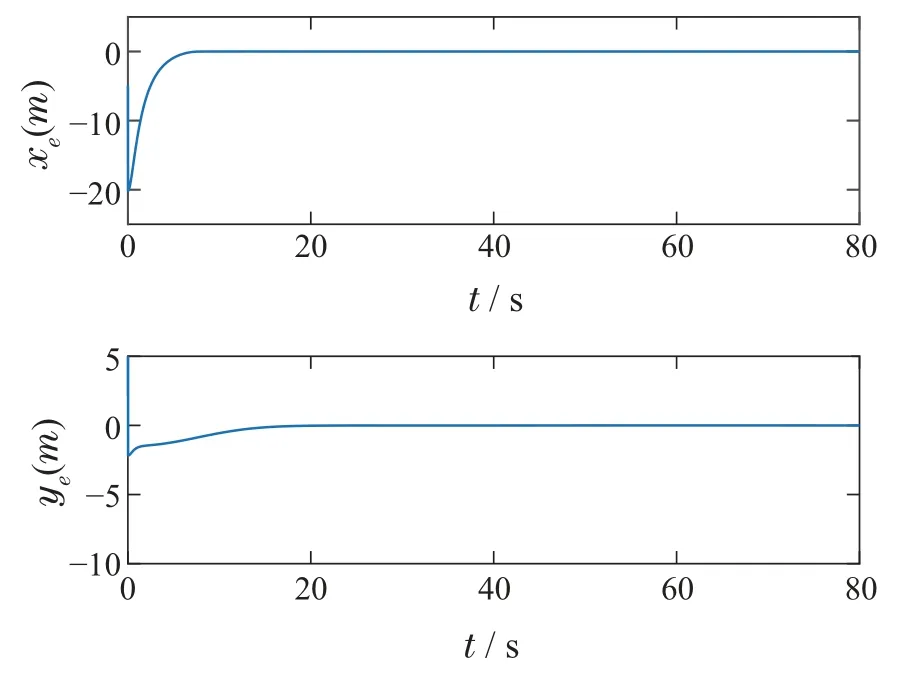
图9 USV路径跟踪误差Fig.9 Along-tracking error and cross-tracking error

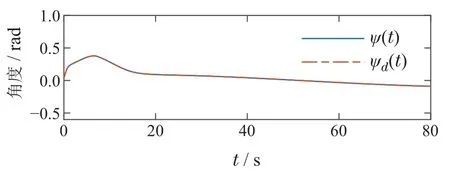
图10 USV偏航角跟踪表现Fig.10 The reference heading and the actual heading angle

由图8可以看出,在相同初始条件下,基于固定时间预测器导航律的无人艇跟踪曲线能更快收敛到期望路径上.

5.3 抗干扰表现

为验证在风浪等复杂等外部干扰情况下,本文所提出的控制方法的有效性,实验3在动力学模型式(2)中加入了时变扰动

并将无人艇期望路径曲线设计为x(θ)θ,y(θ)θ+10 sin(0.1θ),初始位置和姿态角为(x,y,φ)(10,18,0),初始速度和转向角速度为(u,v,r)(0,0,0)[4,24].在引入外部环境干扰后,在选取同样控制参数的条件下,分别使用基于固定时间预测器的制导方法与有限时间预测器的制导方法进行仿真实验,其跟踪表现和跟踪误差分别如图11和图12所示,对期望偏航角的跟踪效果如图13所示.

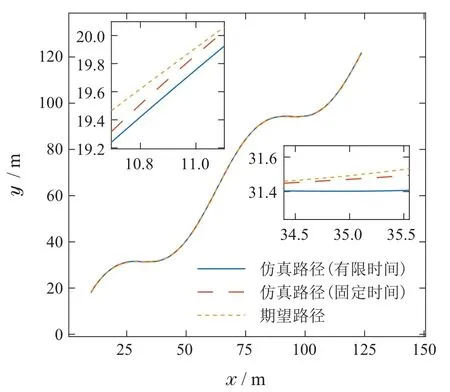
图11 在时变扰动下USV跟踪效果Fig.11 Path following performance with time-varying disturbance

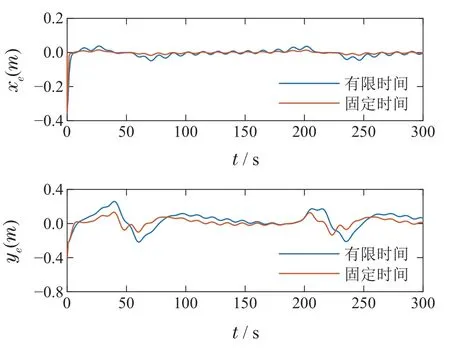
图12 在时变扰动下USV路径跟踪误差Fig.12 Along-tracking error and cross-tracking error with time-varying disturbance

图13 在时变扰动下USV偏航角跟踪表现Fig.13 The reference heading and actual heading angle with time-varying disturbance

图12表明,本文提出的基于固定时间预测器的控制方法能在外部扰动存在的情况下跟踪期望路径,跟踪误差在零附近较小的邻域内变化,且相较于基于有限时间预测器的控制方法,基于固定时间预测器的控制方法收敛时间更短,跟踪误差的波动范围也更小,更稳定.图13为基于有限时间和固定时间两种预测器的制导律所计算出的期望航向角的变化情况,可以看出随着曲线路径曲率变化,计算出的期望航向角也在变化,且期望航向角也会随着风浪等外部扰动发生小幅度波动,但本文提出的路径跟踪方法仍能很好的跟踪期望航向角.

6 结论

对于无人艇的路径跟踪问题,本文首先在传统视线法制导的基础上提出了一种基于固定时间预测器的制导律,将路径跟踪问题转化成艏向角跟踪问题,证明在期望艏向角下,无人艇能跟踪给定路径.对于外部扰动,本文提出的固定时间预测器能预测无人艇跟踪误差,从而补偿环境扰动造成的未知侧滑角,且证明了该预测器预测误差能在固定时间收敛,且收敛时间不依赖于误差初始值.在此基础上文章进一步根据第3节所提出的制导律设计了固定时间收敛的控制器,控制无人艇转艏力矩使无人艇艏向角在固定时间收敛到期望值.经过仿真验证,本文所提出的欠驱动无人艇路径跟踪方法对于直线路径和曲线路径均具有良好的跟踪效果,且能对外界时变扰动进行预测补偿.基于视线法的路径跟踪方法设计简单,稳定性强,但本文设计的控制器只控制方向舵,无人艇以匀速跟踪预设路径.在未来的研究工作中希望对这一问题进行改进,对前向推进力和方向舵力矩同时控制,使无人艇在固定时间跟踪上时变的轨迹.