利用方位角观测的多机器人系统离散分布式最优围陷控制

付瑛博,杨紫雯,朱善迎,陈彩莲

(上海交通大学自动化系,上海 200240;系统控制与信息处理教育部重点实验室,上海 200240;上海工业智能管控工程技术研究中心,上海 200240)

1 Introduction

Due to the advantages of multi-tasking,fault-tolerance and cost-effectiveness [1],the multi-robot system(MRS)is extensively applied in various fields,including area surveillance [2],exploration and mapping[3],etc.When robots execute tasks,detecting and entrapping targets are significant procedures.However,this process is constantly hindered by environmental interference on acquisition of positioning information.Therefore,in practical scenarios,how to drive the multi-robot system to entrap the target in a desired orbit and formation has attracted much attention.

When the environmental condition is ideal,the global positioning system(GPS)can solve the problem of target positioning.Authors in[4]propose a self-propelled particle model to describe the collective behavior of a group of mobile agents to achieve velocity alignment and collision avoidance.Authors in [5] use the global position information of the target known by the leader to achieve annular formation around the target.However,accuracy of positioning information obtained by GPS is low for some tasks.In some cases,it may not even be available in some GPS-denied environments (such as indoor environments and underwater environments,etc),where schemes for entrapping the target based on global positioning information may fail in practice.

Methods are developed for the MRS using one type of indirect measurements rather than global positions to locate and entrap the target.According to the types of measurements,the existing literature based on local measurements can be divided into several categories.Authors in[6]propose a framework of formation shape observers,relative position estimator and distributed controllers with bearing measurements and velocity measurements.In[7],a washout filter and a control law based on distance-only measurement are designed to achieve circular entrapment.Authors in [8] settle the leader-follower formation problem with bearing measurements,to avoid using global positions.In[9],the formation control of multi-robot system using bearingonly measurements is studied to achieve large-scale formation and control its scaling.

However,new methods need to be developed due to the following three reasons.Firstly,including[10-11],most schemes only make agents move on the circle centered at the target or the geometric center of multiple targets.But in the practical environment,the desired shape of the orbit often needs to be adjusted according to the environment[12],where above schemes may fail.Secondly,compared with the continuous-time schemes which are most of the existing works,the discrete-time schemes have received less attention,except [13] and[14].It is challenging to tune gains and set the sampling frequency when the continuous-time scheme is used in practice.Thirdly,there are gains that need to be adjusted in most of the existing schemes,while the process of gains tuning is often manual,such as[15] and[16].Obviously,this method depends on repeated trials and manual experience,which is hard to enhance the performance of the scheme to the best and may even lead to the failure of tasks.

Motivated by the above observations,we develop a discrete-time estimator-controller scheme,where the estimator is designed to estimate relative positions with bearing measurements.Based on estimation,robots can be controlled to entrap the target in an arbitrarily shaped orbit.To improve the performance of the multi-robot system,an optimal gains tuning method is proposed.Compared with most of the current literatures,our main contributions of this paper are as follows:

1) Compared with most of existing algorithms in which the desired orbit is a circle or an ellipse centered on the target [10-11],the shape of the desired orbit in our scheme is arbitrary,so that the control method can be used in various scenarios.The robots only need to know the expected waypoint at the next moment and the current moment for the controller.It is noted that the discrete desired paths can be obtained by sampling the continuous desired trajectories at a fixed frequency using ZOH sampling method.

2) Different from most of the existing algorithms designed in the continuous time domain,and the schemes in the discrete-time domain using distance measurements[13-14],the proposed algorithm is designed fully in the discrete-time domain using bearing-only measurements.And the stability of the overall closed-loop system is thus analyzed in the discrete-time domain,using LaSalle’s theorem for the discrete-time systems[17]and iterative method.

3) We develop an optimal gains tuning scheme for mobile robots to entrap the target so as to speed up convergence of the closed-loop system.The estimator and the controller gains do not rely on manual or random setup.At the same time,the proposed optimal gains tuning method considers the energy cost of robots,avoiding overloaded operation caused by improper gains.

The rest parts of this paper is organized as follows:Section 2 presents notations in this paper and describes the basic contents of the problem.Schemes for path planning and the estimator-controller schemes for path tracking are stated in Section 3 and 4.Moreover,to improve the performance,an optimal gains tuning method is presented in Section 5.Simulation and results are given in Section 6.Section 7 makes a conclusion and further discussion of our work.

2 Preliminaries and problem formulation

2.1 Preliminaries

In this article,C,Z+and R denote the sets of complex numbers,positive integers and real numbers,respectively.|a|denotes the absolute value for a real numberR and‖c‖denotes the model for a complex numberC.For a functionf(x),∇f(x)is its gradient aboutx.j is the unit imaginary number.Re(c)denotes the real part of a complex numberC.

2.2 Problem formulation

We consider a group ofn+1 robots labeled as 0,1,...,n.Suppose that the 0th robot is the leader and the other robots (i1,...,n) are followers.Robots are driven by the discrete-time dynamics[18]

where,C represent the position,velocity of the robotiat timeZ+,respectively,andis the control input,andTis the discrete time interval.Suppose each robot can measure the bearing to the target.Denote the position of target asx*and the relative position from the robotito the target as

where,R represent the distance and the bearing from the robotito the target at timek,respectively.The forward difference of the bearing is given by

In the target entrapment problem,all robots search for the target and surround it in a cohesive manner,including the entrapping formation and orbit.In practical scenarios,it is desirable for robots to maintain a pre-defined formation which can be arbitrarily designed(e.g.a line or a square),and then the formation entraps the target as a whole in a pre-defined orbit(e.g.a circle or an ellipse)at the same time.See Fig.1.

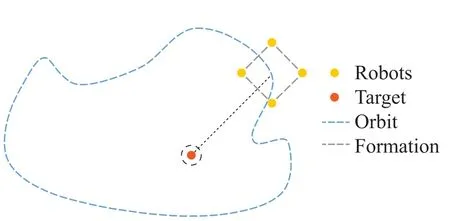
Fig.1 Move on the orbit in a formation

To achieve the goal of target entrapment,the desired path of each robot is usually planned first,which can be presented as follows.

Problem 1Given the desired shape of the formation and entrapping orbit of the multi-robot system,the desired waypoint of each robot at each timekis planned for all the timek≥0.

Remark 1The desired orbit and formation can be designed arbitrarily by choosing corresponding mathematical description of the desired relative position from each robot to the target each time.

To achieve the goal of tracking the desired path,a scheme needs to be designed.So the path tracking problem can be stated as follows.

Problem 2Given the planned path of each robot consisting of the planned waypoint at each time,each robot tracks its desired path using bearing measurements asymptotically.

In conclusion,the target entrapping problem can be solved by two steps: path planning and path tracking.In the first step,the desired paths of robots are planned to guide robots.The second step is that a scheme is proposed to drive robots to track the path planned before.

3 Path planning for an arbitrary formation and orbit

In the process of path planning,a coordinator is developed to let robots in the desired paths maintain a desired formation on the desired orbit.

3.1 Coordination of the desired formation

A virtual system is usually used to lead the moving path of each robot(e.g.[19-20]),whose goal is to keep a relative position from the virtual robotito the target as

whereis the global position of the virtual roboti,represents the distance from the virtual robotito the target,andis the bearing from the target to virtual roboti.Variables are illustrated in Fig.2.

Fig.2 Notations and illustration of path planning

To coordinate the path of each virtual robot,the 0-th virtual robot is defined as virtual leader to lead the formation to entrap the target in a desired orbit,and others are defined as virtual followers to maintain the desired formation.To achieve the above goals,the virtual leader is described by its relative position to the target to design the desired entrapment orbit of the formation by(4)and the virtual followers coordinate their paths from themselves to the virtual leader to maintain a formation,whose paths can be designed as

Linear formation:The linear formation is that robots maintain equally spaced in a line.Given the path of the virtual leader,the linear formation can be designed by describing the fixed relative distance and bearing from each virtual follower to the virtual leader.

The distance between the virtual followeriand the virtual leader in the line can be predefined and the relative bearing from virtual followerito the virtual leaderis same as the bearing from the virtual leader to the targetψ0*.

3.2 Design of the desired orbit of the virtual leader

In order to lead the whole multi-robot system to move on the desired orbit,the path of the virtual leader can be designed by describing the relative distanceand bearingfrom the target to the virtual leader.We take the orbit of Water-drop as an example.

Water-drop:The Water-drop is defined as a combination of a triangle and a semicircle,whose polar equation is given by

whereµis the radius of the orbit of a semicircle for the virtual leader.In this case,the relative bearing varies in a pre-defined angular velocity,that is

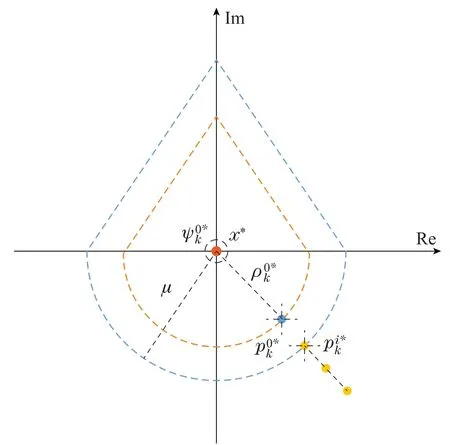
Fig.3 Schematic diagram of the orbit of water-drop and linear formation.

4 Path tracking using bearing-only measurements

To solve Problem 2,an estimator-controller scheme to drive the robot to track the path of the virtual robot is developed.

4.1 Design of estimator using bearing-only measurements

In order to design the controller,the relative position from the robot to the target is estimated first.To this end,an estimator based on the bearing measurements is designed.In order to facilitate the subsequent analysis,a unit orthogonal variable is introduced

whose module is 1.Given the inner product〈a,b〉Re()forC,the following formula:

holds for all timek ＞0,owing to orthogonality property.With this variable,an estimator is proposed to estimate the real-time relative position at each timekas follows:

2) There existζ ＞0 andσ ＞0 such that the persistence of excitation

holds for allkd＞0.

Remark 2Condition 1)can be satisfied by choosing a proper estimator gainwhen the sampling periodTis fixed.And the condition 2)can be satisfied by planning the paths of virtual robots.The angular velocities of robotsare not identically equal to,wheremis an integer.Then,the robots can be led to move around the target and condition 2)about the angular velocities of robotscan be satisfied.

ProofBased on the discrete system model,the forward difference of estimation error can be given as

A Lyapunov function candidate iswhich is obviously a positive definitive function.Its forward difference ΔV()can be obtained that

Under the condition 1) in Theorem 1,it yields that ΔV()≤0.

By LaSalle’s theorem for discrete time systems[17],all trajectories will converge to the maximum invariant setMincluded in ΔV()0 that is

By(15),we can show that the forward difference ofthus also converges to 0,that is

where the first term aboutconverges to 0 by(15).

Therefore,equation (18) together with (15) yields that the second term in(18)converges to 0,that is

Under the the persistence of excitation condition in Theorem 1,for each time instantkd,there existskD≥kdsatisfying that|sin()|＞Φ,whereΦis a positive number,even thoughkdtends to infinity.Thus,together with(19),it can be concluded that

4.2 Design of controller based on estimation

In order to drive the robot to track the path of the virtual robot,a controller based on estimation of the relative position is proposed as follows:

whereis the controller gain.

Remark 3These two conditions are independent of each other,which can be also satisfied independently.Condition a)can be satisfied as stated in Remark 2.And condition b)can be satisfied by choosing a proper controller gainwhen the sampling periodTis fixed.

Based on the the property(13),we have

together with(23)yielding that

By recursion of(25),can be expressed as

Letpk,andis given by

From Theorem 1,we can know thatconverges to 0 under condition a)in Theorem 2,yielding that

At the same time,with the boundedness of initial tracking errorand the condition b) in Theorem 2 that 02,we have

Combining(28)and(29),it can be concluded that

Remark 4The proposed scheme is designed in the global frame,which can be extended to the case of the local frame by involving a rotation variable determined by the difference of orientation.A scheme based on discrete-time consensus algorithms[21] can be put forward to guarantee the alignment of orientation,and the designed estimator and controller can be corrected using the rotation variable.

5 Optimal gains tuning

The above result only guarantees the stability of the overall system.However,the tracking performance needs to be improved since robots can not entrap the target quickly if gains are set improperly.In order to realize the optimization of error tracking,we propose an optimal gains tuning method for each robot to adjust the estimator gainin the estimator(10)and the controller gainin the controller(22).

To guarantee the convergence of the estimation error and the tracking error,conditions about the gains as follows must be satisfied,that are

By considering convergence of estimation error and tracking error and energy cost,the cost function for robotiis set as follows:

wherere,rt,ruare positive numbers representing the weights of the estimation,tracking and energy cost,andkfis the length of time for optimization,respectively.λe(k) andλt(k) are increasing functions aboutkto punish the slower convergence of estimation error and tracking error,respectively.

As for the cost functionJifor roboti,the first part represents convergence of estimation error.The second part represents convergence of tracking error.Moreover,the energy cost is considered in the third part with the module of input.

To conclude,the optimal gains tuning problem can be stated as follows:

whereais the gain vector for robots to adjust.Constraints (32b)-(32d) represent the system model,estimator and controller,respectively.And(32e)-(32f)are constraints of convergence provided in Theorem 1 and Theorem 2.This means that the above optimal gains tuning problem does not affect convergence of estimator(10)and controller(22).

Combining the constraints(32b)-(32d),each term at timekin cost function (32a) can be given using some variables at timekandk-1,which can be denoted by

Given initial estimation of relative positionand input,(33)at timekcan be gotten using bearing measurements from time 0 to timekand planned paths from time 0 to timek+1 by recursion with(32b)-(32d).

At the same time,to make it easier to deal with inequality constraints (32e)-(32f),they can be transformed to

whereβ1,β2are both very small positive numbers.

Therefore,by combining the cost function(32a)with the constraints (32b)-(32d) and transforming the constraints(32e)-(32f),the problem can be transformed to

Obviously,this problem is a nonlinear constrained optimization problem.We know that all inequality constraints (35b)-(35c) are affine functions,satisfying the linearity constraint qualification (LCQ),which is the regularity condition of the well-known Karush-Kuhn-Tucker (KKT) conditions[22].Then the optimal solutiona*must satisfy KKT conditions.

Consequently,by solving the equation and inequality sets in KKT conditions,the optimal gains of each robot will be found.With optimal gains,each robot can estimate the relative position and track its virtual robot fast to entrap the target efficiently.

Remark 5The proposed optimal gains tuning method is offline.Before the multi-robot system entraps the target,information about the environment can be sampled and the environment can be modeled,and simulation can be done.Therefore,better gains can be gotten before performing real tasks,and the system can achieve better performance in real scenarios.

6 Simulation and results

In process of optimization,the weightsre,rt,ruare set as 0.5,0.4 and 0.1,respectively.And the functionsλe(k)andλt(k)are both set asλe(k)λt(k)1-.To show the advancement of the optimal gains tuning method,we use optimal gains in group 1 and random gains in group 2-3 to simulate.And to analyze the influence of parameters on the performance,we simulate with different sampling periods and initial positions in group 4-7,as shown in Table 1.

Table 1 The parameters in simulation

As shown in Fig.4(a)and(b),no matter what gains tuning method is used,the multi-robot system can surround the target on the desired orbit of Water-drop in a linear formation.From Fig.4(c)-(g),the estimation error and the tracking error both converge with different gains,showing the practicability of the estimator and controller.

As shown in Fig.4(c)-(e),the results of group 1-3,both errors converge within 200 in group 1,while ones in group 2-3 converge more slowly.The gap of speeds of convergence shows effectiveness of the proposed optimal gains tuning method.

As shown in Fig.4(c)and(f)-(g),the results of group 1 and 4-5,the sampling period has a little influence on the convergence whenTis not too big,as long as the conditions of convergence are satisfied.But whenTis too big,the convergence speed will be slow.

As shown in Fig.4(c)and(h)-(i),the results of group 1 and 6-7,estimation error and tracking error of three groups converge with different time due to different initial errors.So the robot which is farther from the target spends more time to track the path of its virtual robot.

Consequently,as presented in Fig.4,multiple robots can surround the target on the orbit of Water-drop in a linear formation at different convergence rates,showing the effectiveness of the proposed estimator-controller scheme using bearing measurements.

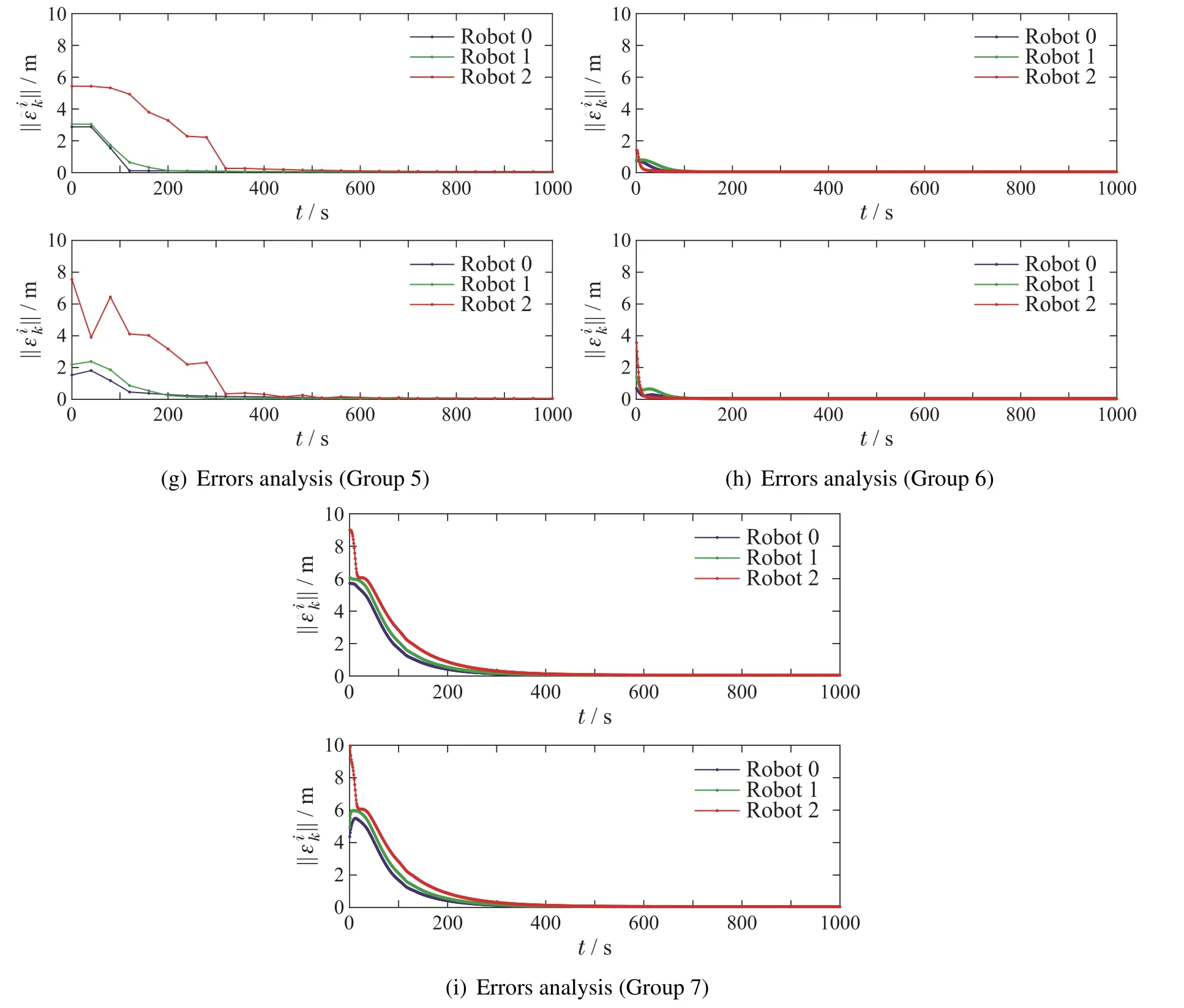
Fig.4 Simulation results with different parameters

7 Conclusions

In this article,we address the target entrapping problem for the multi-robot system with bearing-only measurements by two main steps: path planning and path tracking.The former is solved by designing the paths of virtual robots each time to lead each robot move on a desired orbit in a desired formation.Based on the planned path,the latter is tackled by designing an estimator to locate the target and a controller to track each virtual robot using bearing measurements.Convergence of estimation error and tracking error under given conditions are proven.And an optimal gains tuning method is proposed to speed up convergence of both errors.In the future,the case of moving targets or 3D space can be further investigated.