一种基于双目视觉的箭体晃动在线监测方法

薛春岭，张 峰，刘炼雄

（火箭军工程大学，陕西 西安 710025）

引言

对长时间处于发射台上的液体运载火箭、支撑箭体的支架、发射台钢丝轴承、液压系统等出现塑性变形或故障，可能会引起火箭箭体晃动或倾斜[1]。当晃动或倾斜幅度超出一定范围会使箭体元件受损，不断地累积就会造成箭体倾斜或倒塌等严重后果。因此，必须实时监测火箭箭体的晃动量。通常的方法是，在设备内部安装陀螺仪传感器、3 轴加速度传感器或压力传感器进行结构件晃动监测，并以晃动量监测值来消除误差影响[2]。

设备晃动可能给一些核心元件带来潜在危险，例如当航天设备中的燃料存储箱发生晃动时，会导致燃料泄漏，甚至会因燃料泄漏而发生爆炸。对此，张小虎和LIU 等人以火箭的靶场实验测量为背景，利用摄影测量技术的非接触特点，通过获得人工标识点坐标及实时位姿变换参数的方法，对火箭整体实时晃动进行在线监测，同时利用获取的晃动数值减小测量误差[3-4]。这些研究方式尽管能够实现对箭体晃动实时监测，但由于所采用的技术手段仍存在特征点提取、坐标值求解精度不高及姿态参数解算效率较低等不足，一定程度上影响了晃动测量的精度。

在实际的位姿参数求解过程中，求取位姿变换参数需通过多个点的约束进行有效求解。正如文献[5]中指出，求解体目标的三维位置姿态参数的问题可转化为利用多个标识点求参数的PNP 问题，因而为了求有效解，需对PNP 问题分析讨论。依据有关求解PNP 问题及双目交会测量的相关研究[6-12]，在求解位姿变换参数的问题上，为获取线性唯一解可由P6P 问题简化为P3P 问题，利用3 个以上标识点即可完成对相关参数的直接线性求解。基于此，该文采用双目视觉测量方法构建一种任意2 个标识点间空间距离相等的约束关系，对所建立的标识点坐标系位姿变换参数进行了高精度求解，结合箭体坐标系与标识点坐标系间的几何约束，依据空间物体位姿转换参数获取了结构件晃动的在线监测数据。

1 火箭箭体晃动在线监测方法

为保证箭体晃动测量结果的可靠性和准确性，本文利用2 台单目像机组成双目视觉测量系统和3 个编码标识点实现对标识点坐标的在线测量，并依据标识点的坐标变化求解相应位姿变换的参数，进而间接表征结构件发生的晃动特征量。图1为晃动测量示意图。

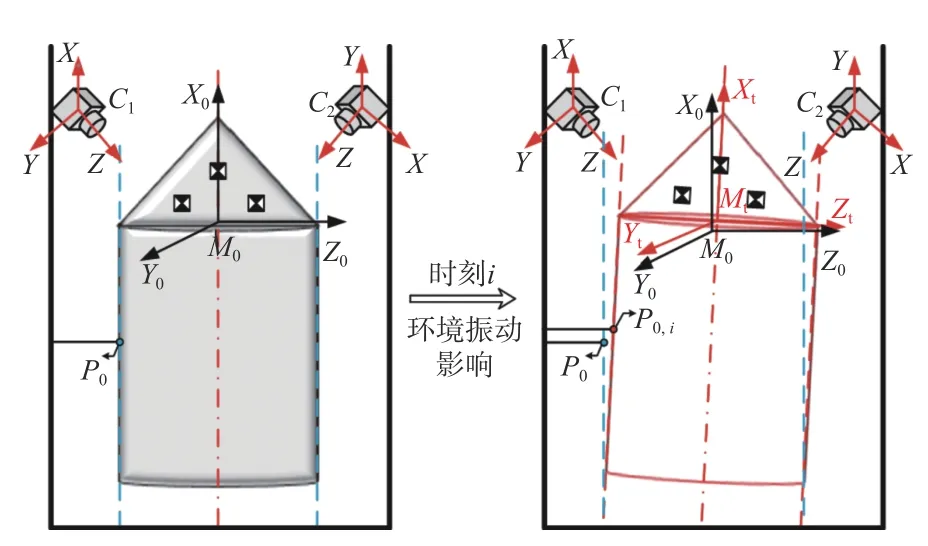
图1 晃动测量示意图Fig.1 Schematic diagram of sloshing measurement

1.1 标识点空间坐标的实时测量

结合图1，建立如图2所示的双目视觉测量原理示意图，所需的像机坐标系为CXYZ（包括C1XYZ和C2XYZ），世界坐标系为WXYZ和箭体坐标系为MXYZ。基于以上模型，对箭体结构的晃动量监测即可转换为初始箭体坐标系M0XYZ与实时箭体坐标系MtXYZ间的位姿参数求解。

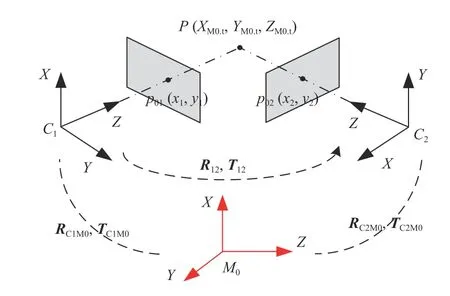
图2 双目视觉测量原理示意图Fig.2 Schematic diagram of binocular vision measurement

用Xm、Xn表示空间某点在m、n坐标系下对应的坐标向量，则2 个坐标系之间转换关系为

式中：Rmn、Tmn分别表示旋转矩阵和平移向量。

结合图2，可得如下转换关系。

像机坐标系CXYZ与世界坐标系WXYZ转换关系为

世界坐标系WXYZ与箭体坐标系MXYZ转换关系为

像机坐标系CXYZ与箭体坐标系MXYZ转换关系为

同时，通过(2)式和(3)式可得像机坐标系CXYZ和箭体坐标系MXYZ转换关系为

由于(4)式和(5)式是等价的，比较得到

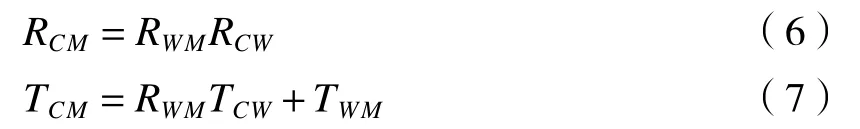
由于双目像机固定，因而像机坐标系与世界坐标系相对位置不变，即RCW和TCW不随时间改变；但箭体坐标系与世界坐标系将随着箭体晃动发生相对改变，即RWM和TWM与时间有关。故像机、初始箭体坐标系间的位姿变换参数RCM0、TCM0可表示为

当标识点P的世界坐标(XW,YW,ZW)随着箭体晃动发生变化时，其在初始箭体坐标系下的坐标(XM0,t,YM0,t,ZM0,t)也必将发生变化。双目视觉测量系统能够同时获取2 组关于标识点坐标的方程，克服了单目像机无法求解3 个未知数的缺点，因而可有效完成对初始箭体坐标的实时测量。当获取了标识点P在2 台测量像机中对应像点p01(x1,y1)和p02(x2,y2)时，依据共线方程可得到如下关系式：

(9)式中包含4 个方程和3 个未知数(XM0,t,YM0,t,ZM0,t)，故根据事先标定好的像机参数K1、K2、RC1M0、TC1M0、RC2M0和TC2M0即可对标识点的空间坐标(XM0,t,YM0,t,ZM0,t)进行实时测量。由于上述线性求解结果易受噪声和初始误差的影响，因此在获取标识点坐标的初始值后，需对其进行误差修正。采用文献[13]的约束条件，以修正后标识点坐标与实际标识点坐标的距离平方和最小为目标函数，优化求 解出精度可靠的坐标值。

1.2 箭体坐标系位姿变换参数实时测量

为有效求解初始箭体坐标系M0XYZ与实时箭体坐标系MtXYZ间的位姿变换参数RM0,t、TM0,t，可将其直接转换为求解不同时刻下标识点坐标在初始箭体坐标下发生的位姿变换：

在实时获取坐标值(XM0,t,YM0,t,ZM0,t)、(XM0,YM0,ZM0)后，可依据(10)式求解不同时刻箭体坐标系的位姿变换参数RM0,t、TM0,t，进而求得箭体晃动量。

由于直接求解的参数结果容易受到扰动因素的干扰，因此在求解过程中对标识点设置了任意2 个标识点间空间距离相等的约束条件。在获得线性求解的参数初值后，按照约束条件对位姿变换参数进行非线性优化，以保证参数精度的可靠性和稳定性。其目标优化函数为

式中：Pi、Pj为像机实时测量得到的标识点坐标；为利用初值坐标和求解出的位姿变换参数进行求解的标识点坐标。

2 位姿变换参数求解流程

在求解了标识点初始箭体坐标系中的实时坐标后，可由其坐标变化求出相应的位姿变换参数，具体求解流程如下。

Step 1:建立箭体坐标系、世界坐标系和2 个单目像机坐标系，并对双目像机内外参数进行初始标定；

Step 2:利用全站仪等设备对编码标识点进行位姿测量，记为初始坐标(XM0,YM0,ZM0)；

Step 3:利用双目像机获取标识点的实时图像，结合相应畸变校正法[14]对图像畸变进行在线校正，并运用(9)式对标识点进行实时测量，记为实时坐标(XM0,t,YM0,t,ZM0,t)；

Step 4:根据步骤2、3 获得的标识点初始坐标值和实时坐标值，求位姿变换参数初始值。

Step 5:利用非线性优化方法求位姿变换参数RM0,t、TM0,t，据此求解箭体晃动值，完成对箭体晃动 量的在线监测。

3 实验验证

由于位姿变化是影响贮存状态箭体晃动的主要因素，而本文在简化其他影响因素的基础上，对箭体晃动的测试实验利用3 轴旋转台验证了位姿变换的影响。实验设备主要包括3 轴旋转台、微视MVC14KSAC-GE6 像机、C3516-M 镜头、自研箭体模拟件和测量仪，相关设备和模拟件如图3所示。

图3 测量实验中相关设备和模拟件Fig.3 Relevant equipment and simulators in measurement experiment

在OpenCV2.4.9 环境下，像机采样频率远高于箭体晃动频率，并对双目像机坐标系与世界坐标系位置进行标定。相关实验数据的对比分析结果和参数标定如图4所示。

图4 双目像机标定实验Fig.4 Calibration experiment of binocular camera

3.1 坐标测量精度验证实验

在坐标测量精度验证实验中，分别将3 个标识点等间距粘贴于标识点坐标系（与箭体坐标系重合）的3 个坐标轴上。首先，在离线情况下完成对2 台像机的高精度标定，并获取其内外参数，具体标定实验见图4所示；然后，利用双目交会原理从不同位置对标识点坐标进行测量，并将其与标准坐标值（由全站仪等辅助设备测量得到的高精度坐标）进行多组对比实验。在标准坐标下，标识点1 坐标为（100.00,0.00,0.00）、点2 坐标为（0.00,100.00,0.00）、点3 坐标为（0.00,0.00,100.00），单位为mm，如图5所示。

图5 标识点位置Fig.5 Location of marked points

为方便实验分析处理，在获取了标识点空间坐标后，将其空间坐标转换至标识点坐标系中，其中每组实验所获取的标识点坐标如表1所示，进行数据处理后的测量偏差如图6所示。由图6 可知，在10 次不同测量实验中，单个标识点测量误差最大值不超0.026 mm、坐标总偏差不超过0.079 mm，偏差平均值为0.063 mm。从实验结果可以看出，文中利用的双目视觉测量方法求解的标识点坐标精度较高，能够满足实际测量和后续位姿参数解算的精度要求。

表1 标识点坐标测量结果Table 1 Coordinates measurement results of marked points 单位为mm

图6 标识点坐标测量误差Fig.6 Coordinates measurement error of marked points

3.2 位姿变换精度验证实验

为进一步验证所提方法求解位姿变换参数的精度，在前面得到标识点坐标的基础上，利用3 轴旋转台，设计了分步位姿变换的实验方案。首先，利用位姿测量方法对标识点坐标系、世界坐标系和旋转台坐标系之间的位姿参数进行标定；然后，通过控制旋转台的实时输出量，对标识点坐标系的实时位姿参数（3 个姿态角Ax、Ay、Az和3 个平移量Tx、Ty、Tz）进行转换求解，以获取实验测量的理论参考数据；同时，利用双目视觉测量系统对标识点坐标进行实时测量，并解算各时刻间的位姿变换参数；最后，通过标准参考数据（控制旋转台输出的角度α0、β0、γ0及利用几何变换求解的平移量Tx0、Ty0、Tz0）与测量数据的对比来验证方法的有效性。

图7 为实验所测量的旋转角参数和平移参数，蓝线为测量值，红线为真实值，滚动角、俯仰角和偏航角依次按照线性增至10°，加载区间分别为0～50 s、50 s～100 s 和100 s～150 s。数据分析结果如表2所示。由表2 可以看出，利用本文方法所得标识点坐标系的实时位姿参数(3 个姿态角和3 个平移量)，Y轴俯仰角误差较大，最大误差为1.27°；Z轴平移量误差较大，最大误差为8.14 mm。

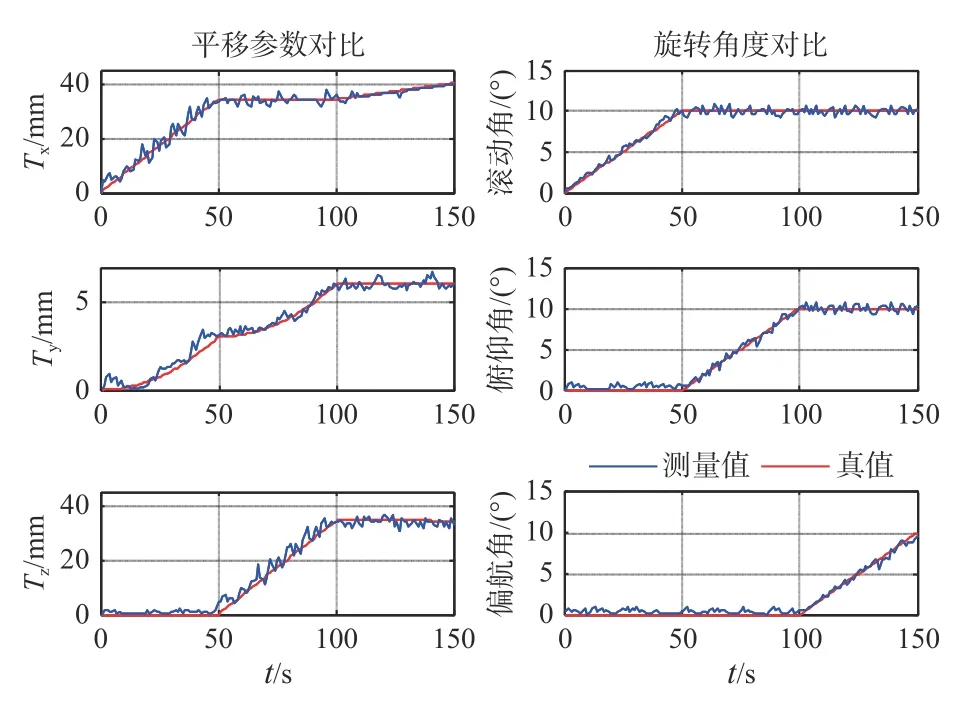
图7 位姿变换参数测量精度实验Fig.7 Measurement accuracy experiment of pose transformation parameters

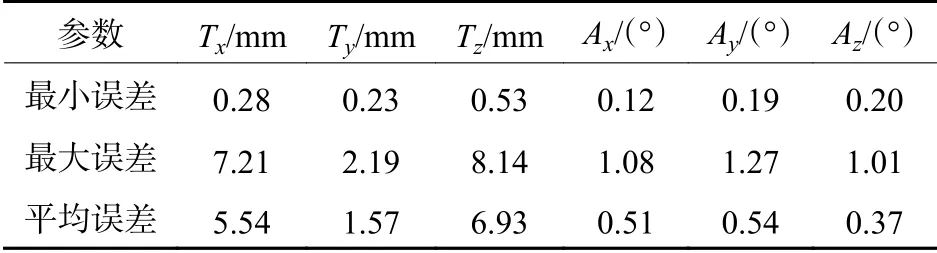
表2 位姿参数解算误差分析Table 2 Error analysis of pose parameter calculation

由表2 可知，测量结果的平移量平均误差不超过6.93 mm、旋转角度平均误差不超过0.54°，与文献[15]～[16]中方法的求解精度相当，有效证明了本文方法求解位姿变换参数的有效性和可靠性。

4 结论

针对火箭整体结构早期晃动量的在线监测，提出了一种基于双目像机实时位姿参数测量的方法。在求解高精度实时坐标中，引入了任意2 个标识点间空间距离相等的约束条件，进一步优化求解了箭体坐标系下的实时坐标值，保证了参数精度的可靠性和稳定性。根据不同时刻间箭体坐标系的位姿变换参数，实现了对箭体结构件晃动量的在线监测。从实验验证结果看，标识点实时坐标的求解精度满足了火箭箭体结构件晃动量的监测需求。