大气湍流对航空光电侦察图像质量影响因素分析

吴雄雄，王惠林，宁 飞，张文博，刘吉龙，王明超

（西安应用光学研究所,陕西 西安 710065）

引言

航空光电侦察系统可以提供高分辨率、高时效性的场景及目标图像，具有侦察距离远、任务模式多、信息获取准确度高、机动性灵活等特点，是当前空中预警监视、战场情报获取等应用的重要侦察方式之一[1-5]。目前国外航空光电侦察系统代表性产品主要有：美国全球鹰上的广域侦察监视系统、Goodrich 公司的DB110 相机、Recon/Optical(ROI)公司的CA295 相机等[6-9]。国内航空光电侦察系统研究起步较晚，装备的航空光电侦察设备大多都是在国外的研究基础上开展进行的。

在航空光电系统成像过程中，光波远距离传播经过大气介质进入光学系统，受到气温、风速、压强等外部条件实时变化的影响，传播介质大气的折射率在时间和空间上产生无规律随机起伏变化，大气折射率呈现出不均匀不规则的分布状态，造成光波相位与振幅紊乱，光波波前产生严重畸变，形成大气湍流效应，加上大气中浮动的水蒸气分子、沙尘等微观粒子对光波传播方向产生散射，导致光波传播路径发生偏折弯曲，严重降低光学系统成像质量。航空光电成像系统输出的图像质量是评价光电系统整体性能优劣的直观因素，直接决定了系统获取复杂外界信息的能力，因此研究航空光电系统成像质量的影响因素一直以来都是光电系统设计师、制造者、使用者们关注的焦点[1]。

航空光电成像系统属于远距离大口径光学侦察系统，目前已经具备高效能的场景实时侦察与监视、目标探测、定位与跟踪等技术功能。在航空光电成像系统观测成像时，由于受到大气湍流的影响，获得的侦察图像产生严重失真，大口径光学成像系统不能充分发挥其良好的成像性能，表现为成像具有模糊、重影和畸变，且照度不均匀等。这些由大气湍流效应带来的干扰，严重影响航空大口径光学系统的成像性能，阻碍遥感观测成像技术的发展。因此，研究大气湍流对航空光电系统成像质量的影响机理，找出大气湍流对航空光电系统成像质量的影响因素非常重要。

本文针对上述需求分析，首先研究了描述大气湍流参数的物理量——大气折射率结构常数与大气相干直径的理论模型，然后使用光学调制传递函数MTF 表征光学系统的成像质量，详细研究了大气湍流效应影响光学系统MTF 的理论模型，并通过实拍图像测试对比验证，给出相应结论。

1 大气湍流参数描述

描述大气湍流的主要参数有大气折射率结构常数、大气相干直径。实际大气十分复杂，描述大气湍流的参数众多，大气湍流参数受天气状况、地理条件、空气洁净度等因素影响，无法实时准确地确定大气湍流的性质[10-12]。在光波传播成像的研究中，尽管流体动力学和大气环流的研究者们希望对大气湍流参数的研究更加丰富，但是对光学工作者来说，为了预估大气光学湍流的成像影响，使用大气折射率结构常数和大气相干直径r0这2 个参数描述大气湍流效应已经足够。

1.1 大气折射率结构常数

大气折射率的不规则起伏变化造成光波传播方向上波前振幅及相位紊乱，严重影响光学系统的成像质量。大气折射率结构常数是用于描述大气湍流强度的物理量，近年来学者们对大气折射率结构常数特征性质的研究越来越多，发展了多种测试手段。受限于大气介质本身的复杂性，很难提出一种通用的模型来阐明大气折射率结构常数的性质。

大气折射率结构常数随着高度和时间发生变化，一般情况下，测量大气折射率结构常数是通过大量的观测试验研究其统计特性。从光学系统空对地成像的适用场景出发，根据实际观测数据，应用比较广泛的是Hufnagel 模型[13]，该模型描述了大气折射率结构常数与高度之间的函数关系，如（1）式所示：

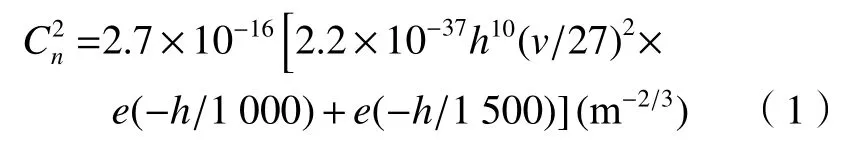
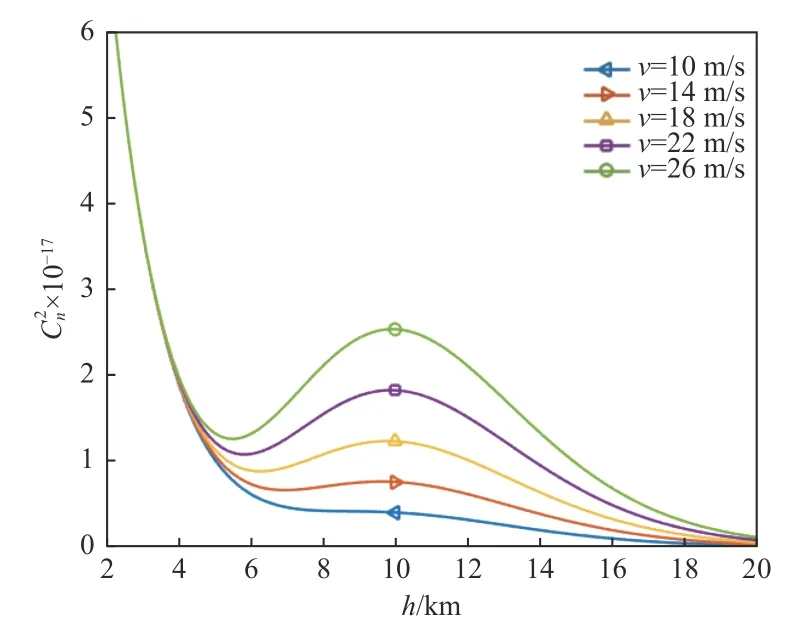
图1 Hufnagel 模型中 曲线Fig.1 curves of Hufnagel model

当高度较低（500 m 以内），适用Tatarski 模型进行描述[14]，如（2）式所示：

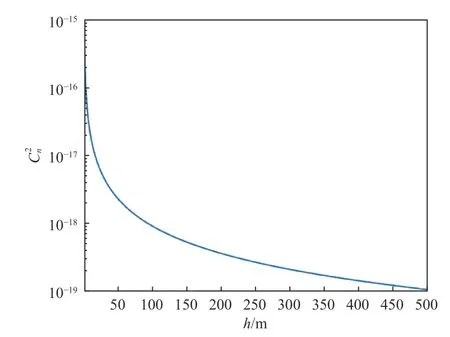
图2 Tatarski 模型中 曲线Fig.2 curve of Tatarski model

1.2 大气相干直径

大气湍流对光波的影响根本上是破坏其相干性，从而导致一系列物理量的改变。各种物理量可分为与相位相关的量和与振幅相关的量。在不同应用系统中，各种物理量的作用是不同的，如在航天通信、激光空间传输的应用中，关心与振幅相关的物理量，而在光学系统成像应用中，关心与相位相关的物理量[10]。在光学系统成像过程中，光波经过湍流大气介质进入光学系统，由于大气折射率不规则的起伏变化，导致传输光的相干性遭到破坏，引起光波相位起伏，产生波前畸变，造成光学图像模糊。

为了在空间尺度描述大气湍流对光波波前扰动强度，Fried 引入了大气相干直径r0[15-16]，其光学成像的物理意义为：在有大气湍流效应的条件下，当光学系统光瞳口径大于r0时，光学系统的衍射极限成像分辨率不再与光瞳口径有关，而是由大气相干直径r0来确定，此时大口径光学成像系统不能充分发挥其大口径的成像优势。

大气相干直径r0与大气折射率结构常数密切相关，对于常见的球面光波在湍流中传播，其大气相干直径r0定义为

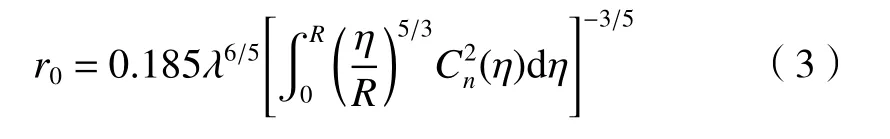
式中η为斜程路径长度，如图3所示。

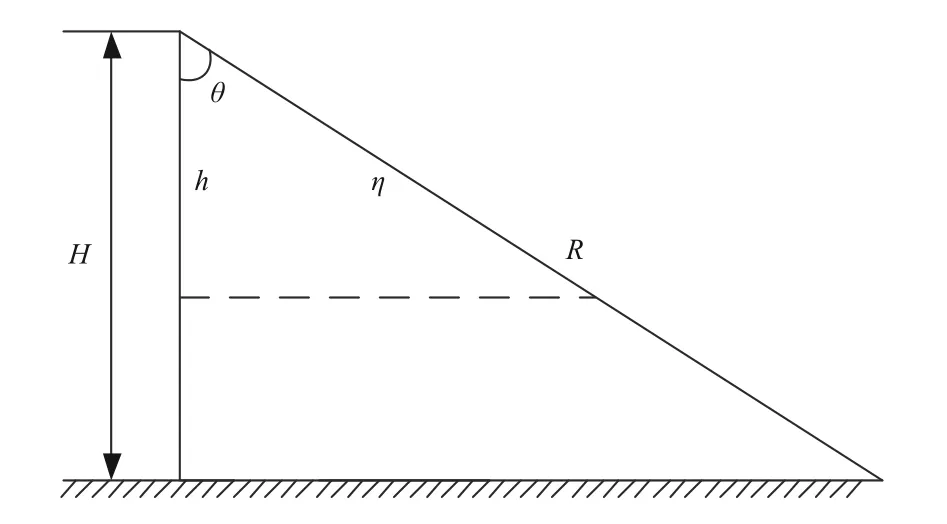
图3 斜程路径长度与高度的几何关系Fig.3 Geometrical relationship between slant path length and height

从图3 中的几何关系可得η=h·secθ，将斜程η用高度h替代，得到(4)式：

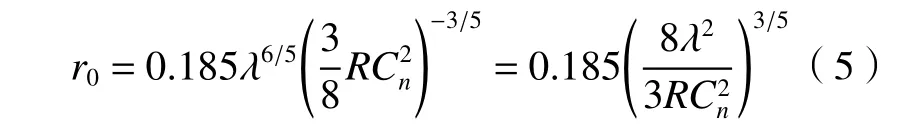
大气相干直径r0表征了大气湍流影响下光学系统成像质量的衍射极限分辨率，反映了大气随机扰动对目标光学成像的影响程度，大气相干直径越大，表示大气条件越好，大气相干直径r0与传播路径长度R的关系如图4所示。

从图4 可以看出，随着路径长度R减小，也就是说随着观测目标距离减小，大气相干直径r0增大。另外大气折射率结构常数减小，也会提高大气相干直径r0。从图4 还可以得到，为了提高大气相干直径，可以提高光学系统相应的成像波长，可以从可见光波段向短波或者中波红外及长波红外波段扩展。

图4 相干直径与路径长度的关系Fig.4 Relationship between coherence diameter and path length

2 大气湍流对光学系统MTF 的影响分析

对于光学成像系统，光学传递函数MTF 是表征评价其成像质量最直接、最全面、最科学、最准确的评价方法[17-18]，已被全世界广泛使用于光学设计、光学成像质量检测和评价等方面。因此，大气湍流对光学系统成像质量的影响可以表征为大气湍流对光学系统MTF 的影响。大气湍流造成的MTF 下降表达式如（6）式所示：

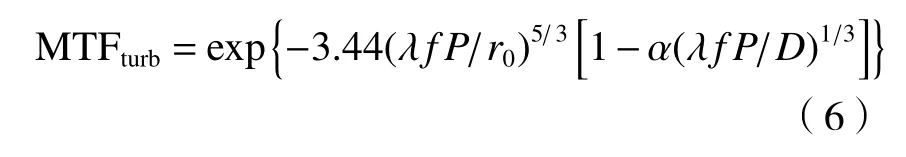
式中：D为光学系统光瞳口径；f为光学系统焦距；r0为大气相干直径；P为空间频率（cycle/mm）。将空间频率P（cycle/mm）转换为物空间的角频率fx（cycle/mrad）：fx=P·f，此时（6）式变为

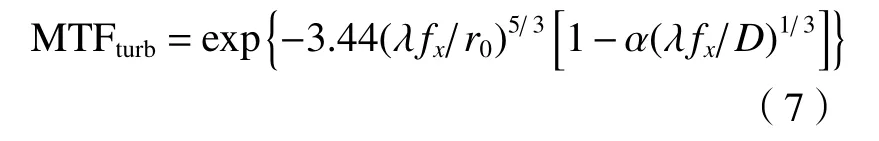
式中α为对应不同条件下的Fried 修正因子[19]。当α=0 时，对应于长曝光情况，α=1 对应于近场短曝光，α=0.5 对应于远场短曝光。其中近场是指光波经过湍流大气介质的距离L较近，满足关系式远场是指光波经过湍流大气介质的距离L较远，满足关系。

大气湍流效应带来的综合光学传递函数MTF下降可以表示为衍射限光学传递函数MTFdiff与大气湍流MTFturb的乘积，即MTFoptics=MTFdiff·MTFturb。对一个圆孔径理想衍射受限光学成像系统，光学传递函数MTFdiff如(8)式所示：

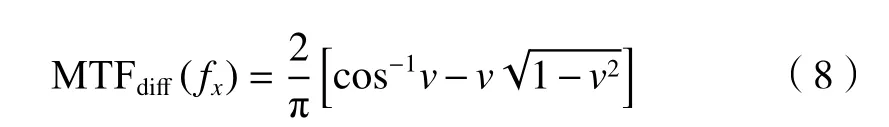
式中：v表示归一化频率，v=fx/foco；fx表示空间频率（cycle/mrad）；foco=D/λ表示光学截止频率（cycle/mrad）。

将大气湍流MTF 用归一化频率v表示，有：

因此，大气湍流效应带来的综合光学传递函数MTF 用归一化频率表示为

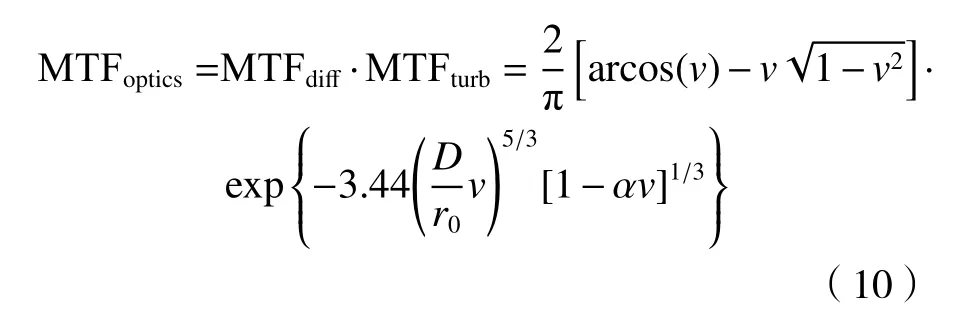
图5 为MTF 曲线图。其中图5（a）为修正因子α=0 时，D/r0分别为0.2、1、2、3 时的湍流MTF 曲线，该曲线反映了大气湍流效应引起理想光学传递函数的下降情况；图5（b）表示了具有湍流效应的综合光学MTF 曲线。

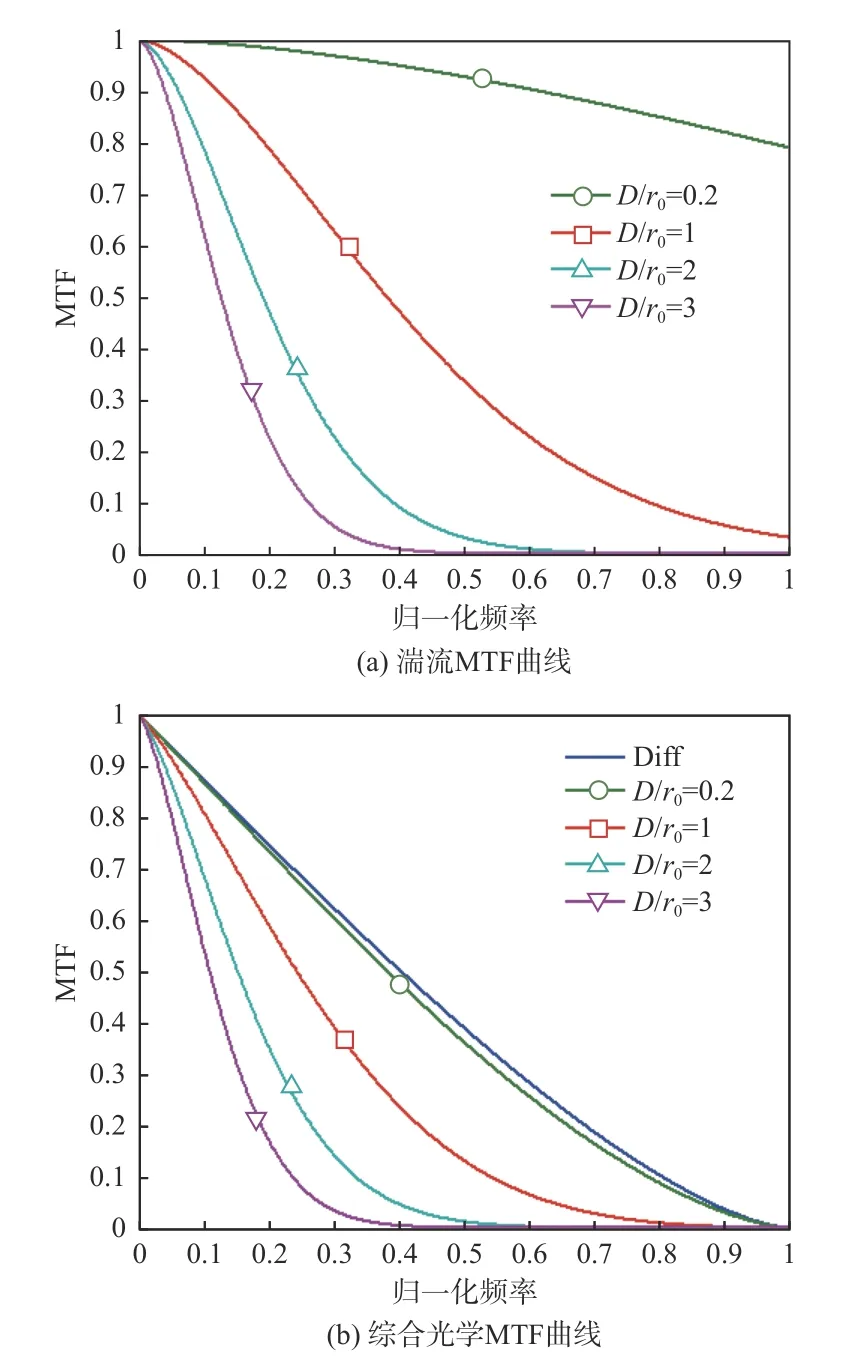
图5 MTF 曲线图（修正因子α=0）Fig.5 MTF curves(correction factor α=0）

图6 为修正因子α=0.5 时，D/r0分别为0.2、1、2、3 时的湍流MTF 曲线及有湍流效应的综合光学MTF 曲线。

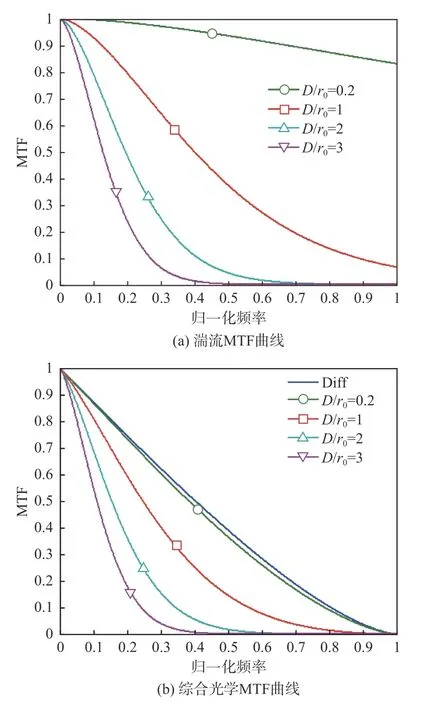
图6 MTF 曲线图（修正因子α=0.5）Fig.6 MTF curves(correction factor α=0.5)

图7 为修正因子α=1 时，D/r0分别为0.2、1、2、3 时的湍流MTF 曲线及有湍流效应的综合光学MTF 曲线。

从图5～图7 这3 组图中可以看出，Fried 修正因子α对湍流大气MTF 的影响较小，进而对光学系统MTF 影响较小；但是，对大气湍流MTF 或者光学MTF 影响较大的是光学系统口径D与大气相干直径r0的比值。文献[19]指出，作为理论模型的经验估计，如果D/r0小于0.2，湍流对光学系统的成像影响可忽略不计。从以上3 组图中的分析可以验证该经验估计，当D/r0小于0.2 时湍流对光学系统的成像MTF 影响可忽略不计。

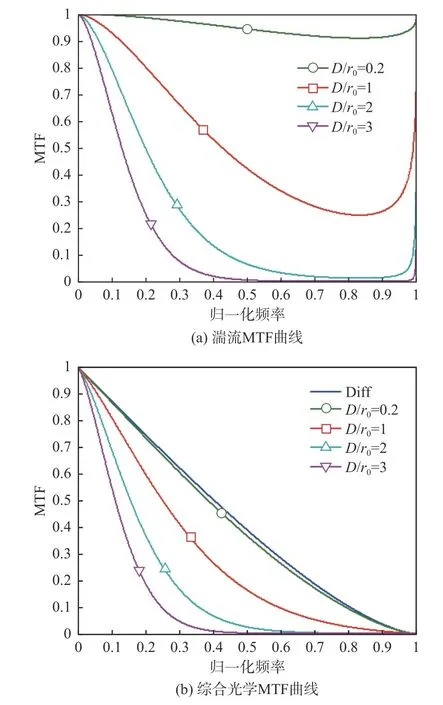
图7 MTF 曲线图（修正因子α=1）Fig.7 MTF curves(correction factor α=1)

3 试验对比分析

为了验证实际航空光电系统受到大气湍流效应影响成像MTF 的理论模型，我们在外场进行试验获取实拍图像。由于航空光电系统挂飞试验条件苛刻，挂飞成本较高，于是采用在高层建筑物平台架设光学系统的方法获取实拍图像。实验时间是早上8：00～11：00，天气晴朗，水平能见度约12 km，相对湿度80%，在该时间段内，大气折射率结构常数受大气温度变化的影响较小[20]。被测光学系统为航空大口径反射式长焦光学系统，架设高度距地约为50 m，距离目标斜距约2 km。根据此条件，首先计算大气湍流效应影响光学系统成像MTF 理论模型中的大气折射率结构常数和大气相干直径r0。

由于被测光学系统架设高度为50 m，因此按照Tatarski 模型（2）式计算大气折射率结构常数。取代入（2）式计算得到在高度为50 m 处的大气折射率结果常数为。

实际光学系统的工作波段为近红外0.6 μm～0.9 μm，取该波段的中心波长λ=0.75 μm，代入（5）式计算大气相干直径，得到大气相干直径r0=102.7 mm，实际光学系统口径φ=250 mm。此条件下，被测光学系统光瞳直径与大气湍流引起的理论相干直径比值约为2.43，远大于上文分析的经验值0.2。

一般情况下航空光电成像属于短曝光。在短曝光时间内，湍流大气可看做为冻结介质，因此短曝光能够减小大气湍流带来的不良影响。由于系统距离目标约2 km，此条件下满足关系式因此属于近场短曝光条件，此时，修正因子α=1，有湍流效应的综合光学系统MTF 表达式如（11）式所示，得到的具有湍流效应的综合光学MTF 曲线如图（8）中蓝色实线所示，图（8）中红色虚线为理想光学系统衍射受限MTF 曲线。

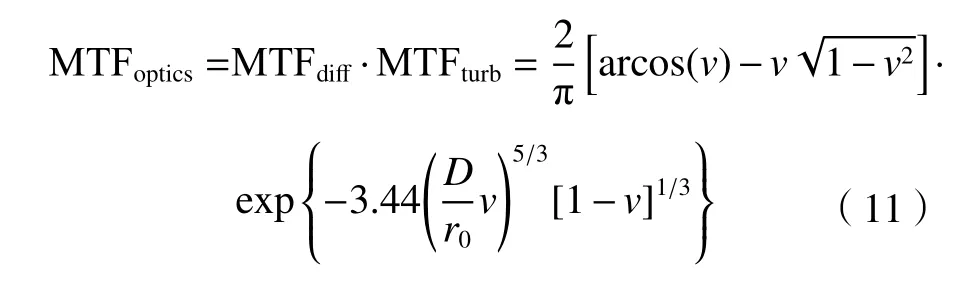
外场实验架设光学系统如图9（a）所示，获取的实拍图像如图9（b）所示，在该图像中选取符合条件的刃边图像，如图9（b）方框所示。根据选取的刃边图像获取其边缘扩展函数（ESF），然后求导得到对应的线扩展函数（LSF），最后通过对线扩展函数进行一维傅里叶变换得到MTF 曲线。整个过程可以通过使用专业图像分析软件Imatest[21]完成，获得的MTF 曲线如图9（c）所示。另外，在实验室光学平台测试光学系统的成像性能，得到的光学系统MTF 曲线如图10所示。

为了将大气湍流效应影响下的理论模型成像MTF、大气湍流效应影响下的实拍图像MTF、实验室条件下测试的MTF 曲线进行对比，将图8、图9（c）、图10 曲线置于同一幅图中。由于实验室测试MTF 曲线中归一化最高频率1 处对应于光学系统的奈奎斯特频率，也就是对应于图8、图9（c）中的0.5 频率处，因此将三者MTF 绘制于同一幅图像中时，取横坐标最大频率为奈奎斯特频率（归一化频率为0.5），如图11所示。

图8 具有湍流效应的综合光学MTF 曲线Fig.8 Integrated optical MTF curve with turbulence effect

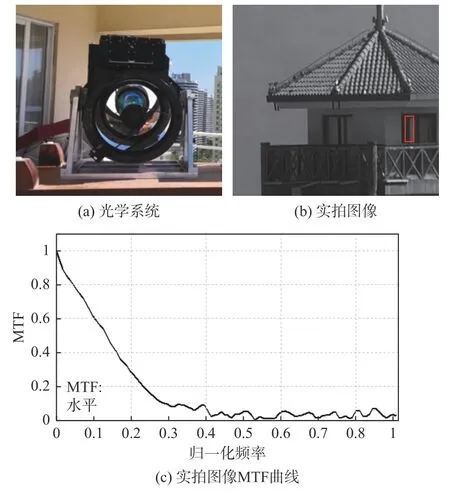
图9 实际光学系统实拍图像及其MTF 曲线Fig.9 Real image of actual optical system and its MTF curve

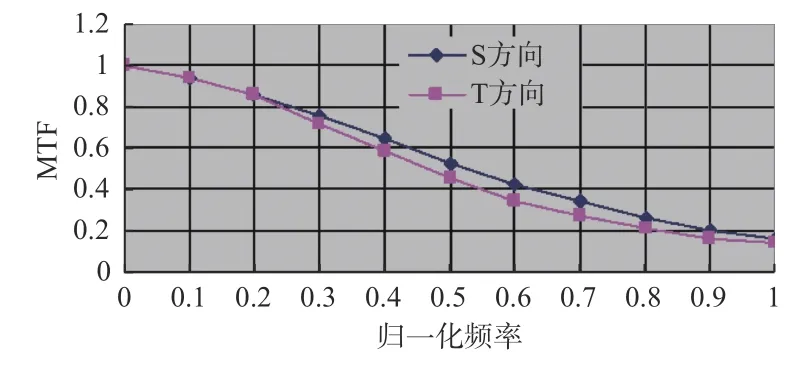
图10 实验室测试MTF 曲线Fig.10 MTF curves tested in laboratory

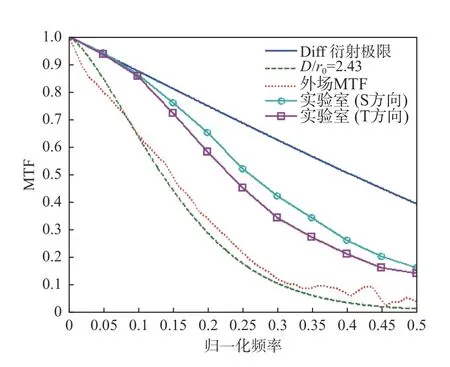
图11 MTF 曲线对比Fig.11 Contrast of MTF curves

从图11 可以看出，在受到大气湍流效应影响的条件下，外场实拍图像MTF 曲线与大气湍流理论模型得到的MTF 曲线（D/r0=2.43）较为接近，验证了实际光学系统受到大气湍流效应影响后的成像MTF 理论模型。还可以看出，实验室测试光学系统的MTF 曲线明显高于外场实拍图像MTF 曲线或者大气湍流理论模型MTF 曲线（D/r0=2.43），这是因为实验室测试光学系统传递函数处于室内静态环境，没有受到大气湍流效应的影响。

4 结论

大气湍流效应严重影响航空光电成像系统的成像质量。本文仿真分析了大气湍流效应对光学成像系统MTF 的影响，并通过实拍图像进行验证对比。得出的结论是：在大气湍流的作用下，单纯提高航空光学系统口径对提高光学成像质量意义不大，应该重点提高大气相干直径，减小大气折射率结构常数，从而减小大气湍流效应带来的成像扰动影响。主要可以采取的措施有提高光学系统成像波长，比如由可见光波段向近红外或者短波扩展；另外可以减小目标观测距离，当光学系统对近距离目标观测时，大气湍流效应减弱明显；但是一般情况下，受限于航空光学侦察系统的应用需求，远距离观测目标不可避免，为了克服远距离观测目标大气湍流对光学系统成像质量的影响，还可以采用自适应光学技术或者图像处理等一些技术手段提升光学系统成像质量。