基于超声特征值的微泄漏孔径识别算法研究

李景林, 杨 录, 刘康驰, 肖旭东, 薛程颢

(中北大学 信息与通信工程学院 电子测试国家重点实验室,山西 太原 030051)

0 引 言

近年来,随着真空容器在航空航天、海洋、日常生活等领域的广泛应用[1～4],人们对其安全性能的检测越发重视。真空容器在生产和使用过程中受焊接、安装、外力挤压等因素的影响,经常会导致泄漏的发生,适时对真空容器进行泄漏检测,可有效避免泄漏事故的发生。

现今,对于真空容器泄漏检测方法主要包括气泡检漏法、真空计检漏法、氦质谱检漏法、超声波检漏法等[5,6],前两种检测方法成本低,检测方法简单,检测灵敏度低,已不适用于工业检漏要求。氦质谱检漏法的突出特点是检测灵敏度高,适用范围广,缺点是检测成本高,检测方法较为复杂。相比于氦质谱检漏法,超声波检漏法检测成本较低、方法简单、灵敏度较高、应用范围广,是一种常用的检漏方法。目前这些泄漏检测方法主要的研究方向在于检测泄漏的有无,而对于泄漏孔径的识别研究较少。

本文在超声波检漏法的基础上提出了微泄漏孔径识别算法。从泄漏孔产生超声信号原理出发,利用双通道超声检测系统对不同泄漏孔径下超声信号进行采集、分析。根据不同泄漏孔下泄漏超声信号强弱关系,提取泄漏超声信号特征值对微泄漏孔径进行表征,为消除特征值受泄漏信号随机性所引起的误判,通过建立数据模型并结合欧氏距离算法,对泄漏孔径进行识别,有效提高了微泄漏孔径识别的准确率和可靠性。

1 泄漏原理与波形特征

与压力容器泄漏原理相似,当真空容器内外存在较大压力差时,在其泄漏孔处就会产生泄漏气体,进而形成湍流,产生超声信号。依据文献研究可知,在频率为40 kHz时泄漏信号具有较强信噪比[7,8],因此选取采集频率为40 kHz泄漏超声信号,来分析泄漏超声信号强度与微泄漏孔径之间的关系是可行的。

在相同真空实验条件下,利用双通道超声检测系统分别对无泄漏时以及泄漏孔径为0.4,0.5,0.6,0.7,0.8,0.9 mm时的泄漏超声信号数据进行采集,得到泄漏超声信号波形与微泄漏孔径的分析结果如图1所示。

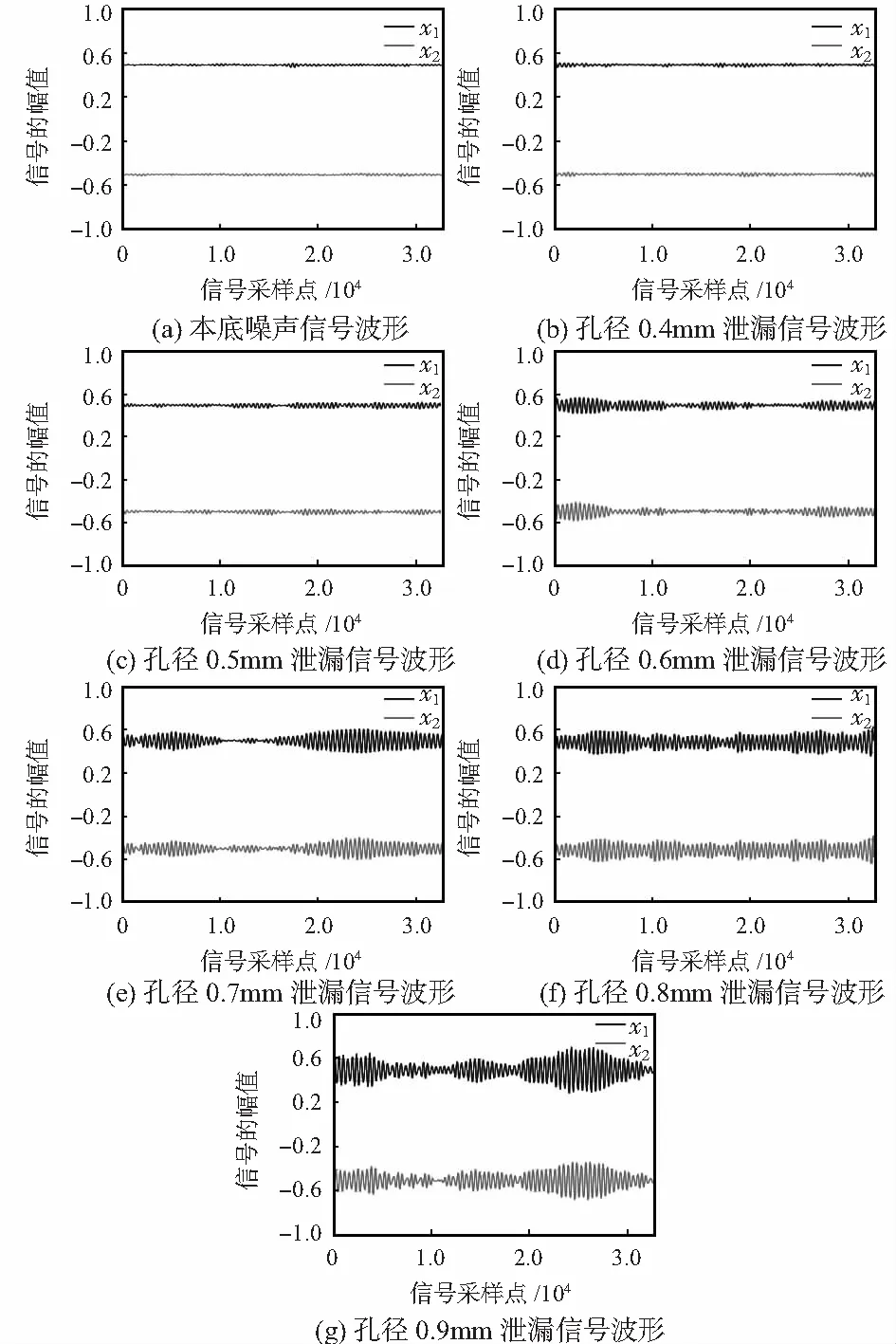
图1 泄漏超声信号波形与泄漏孔径关系

从图1可以看出,随着泄漏孔径从0.4～0.9 mm逐渐增大,其泄漏信号幅值也在增大,这表明可以利用泄漏信号特征值作为参量对微泄漏孔径进行识别。从图1(a)中可以发现,在无泄漏时,也会存在一些微弱信号波形,这主要是由环境噪声和电路噪声引起的,可视为检测系统的本底噪声。因此，本底噪声信号可作为泄漏检测系统判定真空容器有无泄漏状况的参考量。

2 特征值算法与波形分析

2.1 特征值算法公式

为研究泄漏超声信号特征值与微泄漏孔径之间的关系,选取其有效值、互相关有效值、谱峰值、能量值四个特征值进行分析研究[9,10]。将双通道超声检测系统采集到的两路泄漏超声信号设为xi(n),其中i=1,2,采样点数为N,其特征值具体算法公式如式(1)～式(7)。

1)泄漏超声信号的有效值是对信号的平均功率的计算,它能够切实反映出泄漏超声信号在时域信号强度,其有效值rms的计算公式如式(1)所示

(1)

2)互相关函数是指在时域研究两个信号之间的相互关系,广泛地应用于各种信号的处理和检测,如通信、雷达、声纳等领域。在泄漏超声信号中有效信号和噪声信号相关性很小,进行互相关运算有利于噪声信号的进一步滤除[11],因此，选取互相关有效值作为泄漏超声信号的特征值。在进行互相关运算时为减少线性乘累加的过程,提高运算速度,采用快速傅里叶变换(fast Fourier transform,FFT)进行互相关运算[12]。互相关有效值计算过程如下:

首先，对信号进行FFT运算,将任意一路采集的超声信号x(n)分解为偶数与奇数的两个序列之和,即

x(n)=xe(n)+xo(n)

(2)

k=0,1,…,N-1

(3)

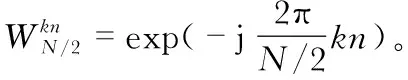
然后,对两路信号数据进行快速傅里叶逆变换(inverse FFT,IFFT),得到互相关函数,并计算其有效值

(4)

(5)

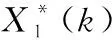
3)泄漏超声信号的谱峰值反映了信号在频域某频率点上的最大信号能量,谱峰值越大,信号在该频率点的能量越强,而其能量值反映了泄漏信号在整个频域内信号能量强弱。计算泄漏超声信号谱峰值时先对信号x(n)进行FFT运算,得到X(k),取其绝对值的最大值即为谱峰值。

4)其能量值计算公式为

(6)

由于以上四个特征值的数值结果存在跨值域较大问题,不利于算法结果统一观察分析,故对信号特征值进行取对数操作,如式(7)所示

TZp=20×log 10(tzp)

(7)

式中p=1,2,3,4;tzp为以上泄漏信号的四个特征值。

2.2 特征值与漏孔关系分析

为有效分析泄漏超声信号特征值与微泄漏孔径的关系,利用双通道超声检测系统分别在无泄漏时和泄漏孔径为0.4,0.5,0.6,0.7,0.8,0.9 mm时,随机采集25组泄漏数据。

泄漏超声信号有效值与微泄漏孔径的分析结果如图2,泄漏超声信号互相关有效值与微泄漏孔径的分析结果如图3。

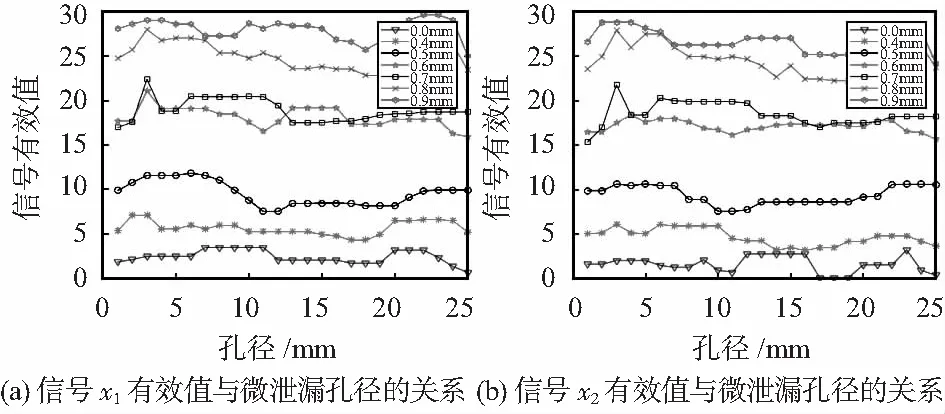
图2 泄漏超声信号有效值与微泄漏孔径的关系

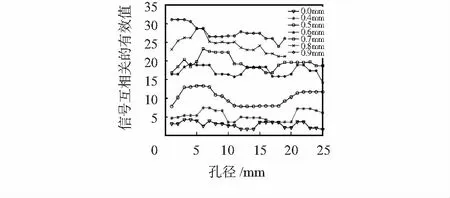
图3 信号x1,x2互相关的有效值与泄漏孔径的关系

从图2,图3可以看出,泄漏超声信号有效值和互相关的有效值呈现相同的规律性:随着泄漏孔径的逐渐增大,它们的幅值也在逐渐递增。存在相邻泄漏孔径之间,其泄漏超声信号特征值的值域出现交叉混叠现象,因而不能直接将有效值和互相关有效值作为识别微泄漏孔径的标量。

泄漏超声信号谱峰值与微泄漏孔径的分析结果如图4。

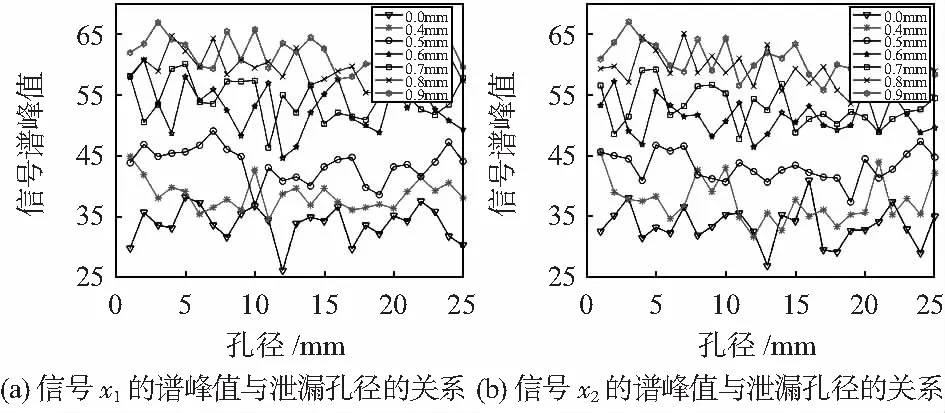
图4 泄漏超声信号谱峰值与泄漏孔径的关系

从图4可以看出,由于泄漏超声信号谱峰值更易受信号随机性的影响,导致不同泄漏孔径下的谱峰值在值域上波动明显,混叠现象严重,不易区分泄漏孔径与谱峰值之间的关系,因此，泄漏超声信号的谱峰值不能作为判断泄漏孔径的特征参量。

泄漏超声信号能量值与微泄漏孔径的分析结果如图5。

图5 泄漏超声信号能量值与微泄漏孔径的关系

从图5可以看出,与泄漏超声信号有效值在不同泄漏孔径下对应关系相似,在频域的能量值随着泄漏孔径的增大,呈现递增规律,也存在相邻泄漏孔径对应的信号能量值出现交叉混叠现象,导致泄漏超声信号的能量值也无法直接作为识别泄漏孔径的特征参量。

3 模型建立与算法处理

从泄漏超声信号特征值与微泄漏孔径的分析结果来看,受泄漏超声信号随机性的影响,其特征值在一定值域范围内具有随机性,导致相邻泄漏孔存在交叉混叠现象,因此，不能直接将泄漏超声信号特征值作为判断泄漏孔径的参数。为利用泄漏超声信号特征值对泄漏孔径进行表征,采用泄漏超声信号特征值建立数据模型,并结合欧氏距离算法的方法对微泄漏孔径进行识别。

根据泄漏超声信号特征值与微泄漏孔径的分析,选取泄漏超声信号的有效值、互相关有效值、能量值作为数据模型矩阵中的元素。如式(8),建立信号特征值的数据模型矩阵,用YN×M表示泄漏信号特征值模型矩阵

(8)

式中n为不同的泄漏孔径,m为同一孔径下取样次数。

引用欧氏距离算法,设xi为待检测孔径的泄漏信号特征值,yi为YN×M中泄漏超声信号特征值元素,其公式为

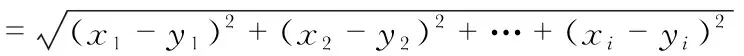
(9)

式中i=5,为同一泄漏孔下取样次数;已知当d(xi,yi)越小时,表示两者的相似度越大[13]。通过将待检测孔径的信号特征值代入数据模型中进行欧氏距离运算,比较各个孔径下欧氏距离值的大小,欧氏距离值最小值对应的孔径即为待检测孔径的大小。

4 实验结果与分析

由于泄漏超声信号能量值远大于其有效值和互相关有效值,这将影响欧氏距离算法判断,因此，将信号有效值和互相关有效值作为数据模型矩阵中判断微泄漏孔径的一组特征值元素,将信号能量值作为另一个数据模型矩阵中判断微泄漏孔径的特征值元素。

将两个数据模型应用到双通道超声检测系统中,并通过欧氏距离算法对微泄漏孔径进行识别。在测漏实验平台上,对真空容器无泄漏时以及泄漏孔径为0.4～0.9 mm时的6种泄漏状态分别进行50次泄漏识别实验,检验此方法对微测漏孔径的辨识正确率,实验结果如表1和表2所示。

表1 泄漏超声信号有效值和互相关有效值模型对泄漏孔径识别实验结果

表2 泄漏超声信号能量值模型对泄漏孔径识别实验结果

从表1和表2可以看出:这两组泄漏超声信号特征值数据模型对真空容器微泄漏孔径的辨识正确率都比较高，达90 %以上,误差识别仅为0.1 mm,达到了真空容器微泄漏孔径识别要求。通过两组试验结果对比发现:实验一的结果在整体方面要比实验二的结果要好,其对微泄漏孔径的辨识正确率高达92 %以上,因此，以信号有效值和互相关有效值建立的数据模型,可有效提高微泄漏孔径检测识别的准确率。

5 结 论

通过对真空容器泄漏超声信号的研究,本文提出了一种微泄漏孔径识别方法。采用特征值数据模型结合欧氏距离算法的方式,有效避免了泄漏信号随机性带来的误判,实现了微泄漏孔径准确识别。通过将此方法应用到双通道超声检测系统中,并经过多次实验验证,以信号有效值和互相关有效值建立的数据模型对微泄漏孔径的辨识正确率大于92 %,具有较高的准确性,能够完成微泄漏孔径识别任务。此微泄漏孔径识别方法为泄漏超声检测技术只能检测泄漏有无,而不能识别泄漏孔径做出完善。下一步需要提高泄漏检测系统的灵敏度和抗噪性能,以便能够对0.3 mm以下的微泄漏孔进行识别。