圆壳体振弦式陀螺驱动设计与振动特性分析*

陈志龙， 刘 鹏， 黄 鸣， 舒 凯

(1.南昌理工学院省级重点实验室,江西 南昌 330044； 2.中国铁路广州局集团有限公司广州车辆段,广东 广州 510080；3.华东交通大学 机电与车辆工程学院，江西 南昌 330013)

0 引 言

振动式陀螺是一种结合微机械加工与微电子工艺的角速度传感器[1]，与传统旋转式陀螺相比具有体积小、重量轻、功耗低、易于集成等优点，在车辆驱动防滑转系统(ASR)、相机防抖系统、机器人姿态感知系统、武器平台稳定系统、炮弹制导等领域得到了广泛的应用[2,3]。文献[4,5]介绍的振动式陀螺均采用静电力驱动，采用静电力驱动的陀螺具有功耗低的特点，但其驱动力过于依赖驱动电压，小电压难以产生足够的驱动力，故无法适应系统集成与微电子器件的发展趋势[6]。文献[7～10]介绍的振动式陀螺均采用电磁力驱动，采用电磁力驱动的陀螺特点是驱动力取决于驱动电流和磁场强度，相比于静电力驱动方式受尺寸效应影响小，能够在有限的体积和电压限制下，实现更大的驱动力和驱动位移。近几年,随着超高精度的半导体加工工艺和装配工艺的发展，一直限制陀螺电磁驱动方式研究的加工装配问题能够得到很好的解决，电磁驱动方式凭借其电压低、响应快、驱动效率高、适用范围广等优点成为陀螺驱动的研究热点[11,12]。

1 振弦式陀螺的工作原理与驱动动力学模型

1.1 振弦式陀螺工作原理

图1为振弦式陀螺的简化模型。质量块m固连在旋转坐标系的xy平面内，模型具有2个振动模式，每个模型都简化为弹簧—阻尼—质量模型。假定质量块在y方向受到某种激励作用而受迫振动，而z轴有角速度Ω输入时，质量块在x方向就会受到交变的哥氏力作用而沿x轴方向产生诱发振动，从而可通过振弦的频率检测，测出角速度输入量。

图1 振弦式陀螺的简化模型

1.2 振弦式陀螺驱动动力学模型

当振弦式陀螺在驱动电路的作用下振动时，其驱动方向的运动可以等效成如图1所示的质量弹簧阻尼系统。驱动框架和质量块的质量和设为my,质量块的质量设为mx，弹性系数设为ky,阻尼系数设为cy，驱动信号在驱动框架上产生的安培力设为Fac，则驱动模态的动力学方程为

(1)

Fac=Fysinωt

(2)

方程的解为驱动框架振动的位移，其频率与施加的安培力相同

x=Aysin(ωt+φy)

(3)

(4)

(5)

式中Ay和φy分别为驱动框架振动位移的幅值和相位，而通过式(4)可知，哥氏力的的幅度与驱动框架振动速度的幅值Ayωd成正比，只有使驱动信号频率稳定在驱动模态固有频率，才能使哥氏力的幅度稳定且足够大。

当ω=ωd时，式(3)可简化为

(6)

2 振弦式陀螺驱动模型与结构方案

2.1 振弦式陀螺驱动模型

要建立电磁驱动的电学模型首先需要对电磁驱动电力系统进行简化，图2为经过简化后的电磁驱动等效图[13]。

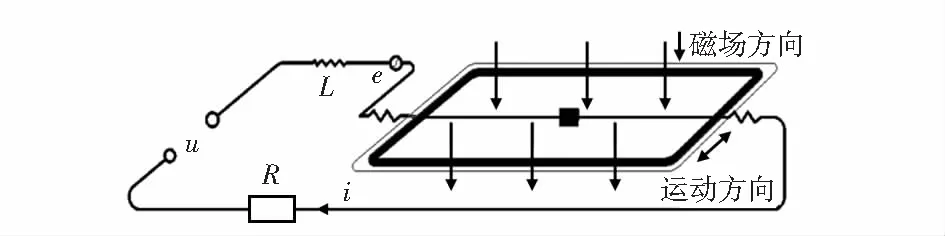
图2 电磁驱动电路简化模型

按图2所示，内环驱动结构外部驱动交换电压幅值为u，线圈的等效电感及等效电阻分别为L,R，电流i在磁场中产生的感生电动势为e。由电路的基尔霍夫第二定律可得到上述模型电压动态平衡方程

u=Ldi/dt+Ri+e

(7)

e=δB/v

(8)

当模型处于稳态时，有di/dt=0，此时可得到模型的电压稳态平衡方程

(9)

2.2 驱动整体结构方案

电磁驱动结构作为振弦式陀螺的主要部件，线性良好的电磁驱动结构有利于提高振弦式陀螺的性能，简化控制难度。振弦式陀螺电磁驱动初步结构模型如图3所示。它是由一对U形折叠梁为支撑的驱动框架和一对永磁体组成的，内环驱动结构位于永磁体边界内，获得均匀的磁感应强度。

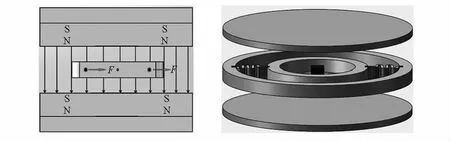
图3 电磁驱动结构设计示意

3 振弦式陀螺驱动结构设计与驱动仿真分析

根据图3所示结构建立圆壳驱动模型，如图4 所示。该驱动模型主要的几何参数有内环半径R,内环宽w1,内环厚度w2,敏感质量块边长d1,U形驱动梁厚度t1,U形驱动梁宽度t2。

图4 电磁驱动电路简化模型

3.1 U形折叠梁结构设计

振弦式陀螺驱动梁结构支撑采用中心单支点结构支撑以降低残余应力以及驱动框架重力对梁的影响。在驱动梁结构振动时，驱动梁的平面运动表现为弯曲变形，对一般的驱动梁，其径向位移与弹性梁的应变能为

(10)

(11)

以右侧U形折叠梁为分析，把U形折叠梁左端固连在外环内圈，驱动力F施加在x方向内环驱动框架上，则模型可以简化为图5所示的等效分析图，其中t1,t2分别为U形折叠梁的宽度与高度。

图5 U形折叠梁结构示意

在U形折叠梁的WO段，连接驱动内圈长度为l3，则轴向拉力N1(x)与x方向挠度δ1为

N1(x)=F，0≤x≤l3

(12)

(13)

在U形折叠梁的LM段，长度为2l，则弯矩M2(x)与x方向挠度δ2为

M2(x)=Fx,-l≤x≤l

(14)

(15)

在U形折叠梁的DE段，半径为r，则弯矩M3(x)与x方向挠度δ3为

M3(x)=F(l2+r+rsinα)， 0≤α≤π

(16)

(17)

在U形折叠梁的DC段，长度为l2，则弯矩M4(x)与x方向挠度δ4为

M4(x)=Fx，r≤x≤r+l2=l

(18)

(19)

在U形折叠梁的BC段，半径为r，则弯矩M5(x)与x方向挠度δ5为

M5(x)=Fr(1-sinα),0≤α≤π/2

(20)

(21)

在U形折叠梁的AB段，连接驱动内圈长度为l3，则轴向拉力N6(x)与x方向挠度δ6为

N6(x)=F,0≤x≤l1

(22)

(23)

环形驱动内环为超静定结构，在工作模态振动时，径向形变主要由弧形梁与纵向直梁的弯曲变形组成，水平直梁的拉伸形变可以忽略不计。得到单个U形折叠梁的径向刚度系数为

(24)

对于环向波数为n的驱动内环圆环，其等效刚度kr为

(25)

式中R与υ分别为驱动内圈的半径与材料的泊松比。

因此环形谐振子驱动模态的刚度系数为

Kτ=Kr+Ks

对振弦式陀螺频率检测梁结构分析时可利用瑞利能量法得到振弦式陀螺机械结构各阶振动模态的谐振频率式

(26)

式中Kτ为梁连接方向τ的刚度系数；mτ为线圈驱动框架等效质量。

3.2 U形折叠梁结构振动分析优化

在分析U形折叠梁结构参数对振弦式陀螺驱动模态谐振频率的影响时，可采用单一变量原则方法，应用Ansys有限元软件进行分析。U形折叠梁结构参数仿真分析条件为：驱动框架采用不锈钢材料，U形折叠梁采用铜铝合金材料，线圈驱动框架采用等效质量，激振力为10 mN，两U形折叠梁连接端面全约束进行仿真，仿真效果如图6所示。

图6 振弦陀螺驱动仿真效果

3.2.1 U形折叠梁宽度对驱动频率的影响

选择U形折叠梁有效长度为3 mm，厚度为0.2 mm，考虑振弦式陀螺的设计尺寸与U形折叠梁纵向刚度，取U形折叠梁宽度为0.4～1 mm，步长为0.2 mm进行仿真，分析数据处理结果如图7所示。

图7 U形折叠梁宽度对驱动频率的影响

从图7(a)可知，随着宽度的增加，各阶模态频率有上升趋势，一阶模态上升的幅度较小，且前二阶模态都低于2 kHz；从U形折叠梁宽度与模态频率的关系图7(b)可知，三模态频率值大于且从仿真分析可得三阶模态为驱动结构所需驱动频率。综合考虑振弦式陀螺驱动结构抗振性以及抵抗内环驱动结构重力因素的刚度问题，选择U形折叠梁宽度在1 mm；这样有利于在电磁驱动时受力，且纵向刚度可以很好的抵抗内环驱动结构的重力，很好的抵抗外界频率的干扰。

3.2.2 U形折叠梁厚度对驱动频率的影响

选择U形折叠梁有效长度为3 mm，宽度为1 mm，考虑振弦式陀螺的设计尺寸与U形折叠梁纵向抵抗重力刚度，取U形折叠梁宽度为0.1～0.5 mm，步长为0.1 mm进行仿真，分析数据处理结果如图8所示。

图8 U形折叠梁厚度对驱动频率的影响

从图8(a)可知，随着U形折叠梁厚度的增加，各阶驱动模态频率逐渐增加，这是由于U形折叠梁厚度的增加使得U形折叠梁刚度系数增加，但前四阶模态频率增加较慢。从图8(b)可知，前二阶模态频率低于2 kHz，从仿真分析可得三阶模态为驱动结构所需驱动频率，综合考虑不让驱动频率过大和振弦式陀螺抗振性，选择二阶模态频率低于2 kHz，三阶模态频率低于3 kHz，选择U形折叠梁厚度应在0.2～0.3 mm。

3.3 内环驱动结构尺寸对驱动的影响

仿真条件为：驱动框架采用不锈钢材料，U形折叠梁采用铜铝合金材料，线圈驱动框架采用等效质量，激振力为10 mN，两U形折叠梁连接端面全约束进行仿真。

3.3.1 内环驱动结构厚度对驱动的影响

仿真时，内环驱动结构的宽度为1 mm，有效内径为6 mm，外径为8 mm，考虑振弦式陀螺的内环驱动结构受力、线圈的布线、内环驱动结构的质量等问题，取内环驱动结构的厚度为1～2 mm，步长为0.2 mm，进行仿真，分析数据处理结果如图9所示。

图9 内环驱动结构厚度对驱动频率的影响

从图9(a)可知，随着厚度的增加三、四阶模态频率有下降趋势，而其他阶模态频率变化不大，在振弦式陀螺驱动仿真中，三阶模态为所需驱动模态；从图9(b)可知，为了使驱动模态频率不低于2 000 Hz，这样有利于避免低频对驱动频率的影响，同时也有利于高阶频率对检测频率的过滤，考虑振弦式陀螺抗振性、内环驱动结构质量、后续零件的装配因素，选择内环驱动结构厚度在1 mm。

3.3.2 内环驱动结构宽度对驱动的影响

仿真时，选择内环驱动结构的厚度为1 mm，外径为8 mm，考虑振弦式陀螺的内环驱动结构受力、线圈的布线、内环驱动结构的质量、振弦式陀螺的整体尺寸等问题，取内环驱动结构的宽度为1～2 mm，步长为0.2 mm进行仿真，分析数据处理结果如图10所示。

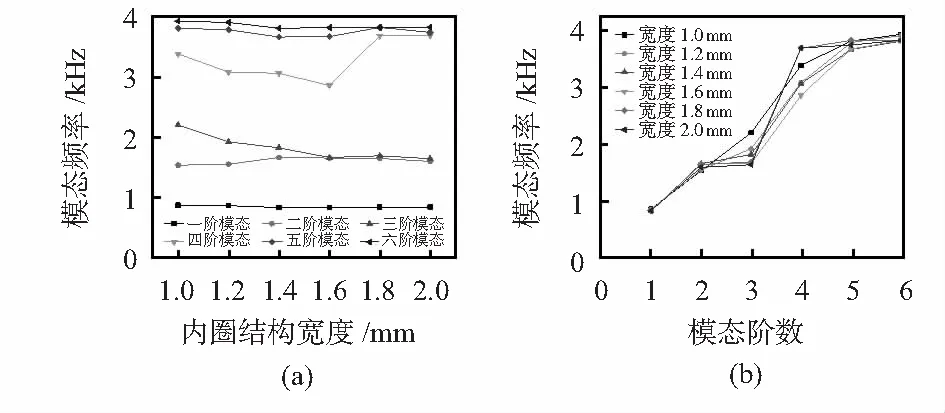
图10 内环驱动结构厚度对驱动频率的影响

从图10(a)可知，随着内环驱动结构宽度的增加，低阶模态频率变化较小，而三阶模态频率有下降趋势，在内环驱动结构宽度在1～1.2 mm之间时，三阶模态频率虽有微幅下降，但模态频率趋于2 000 Hz。从图10(b)可知，考虑振弦式陀螺抗振性、内环驱动结构的重力、后续零件的装配因素，以及考虑振弦式陀螺驱动仿真中，三阶模态为所需驱动模态，且须保证驱动模态频率不低于2000 Hz，选择内环驱动结构宽度应在1 mm。

4 振弦式陀螺驱动轴向重力敏感性仿真与谐响应分析

4.1 振弦式陀螺驱动轴向重力敏感性仿真分析

一般在实际情况下，振弦式陀螺驱动始终承载重力作用，按照安装平面的不同，将受到x向、y向、z向三个不同方向的重力的影响，在此，利用Ansys软件进行分析，考察振弦式陀螺驱动结构在三个方向上10 mN作用下的结构变形和应力分布情况。

4.1.1x方向的重力影响

在x方向施加10 mN载荷时，分析得到的结构整体变形云图和应力分布情况如图11所示。从分析数据中得出，结构的最大位移为0.120 μm。最大应力出现在U形折叠梁外侧连接处。

图11 x方向驱动结构整体变形和应力分布云图

4.1.2y方向的重力影响

在y方向施加10 mN载荷时，分析得到的结构整体变形云图和应力分布情况如图12所示。从分析数据中得出，结构的最大位移为4.244×10-2μm。最大应力出现在驱动U形折叠梁外侧连接处。

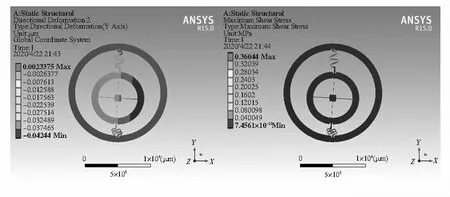
图12 y方向驱动结构整体变形和应力分布云图

4.1.3z方向的重力影响

在z方向施加10 mN载荷时，分析得到的结构整体变形云图和应力分布情况如图13所示。从分析数据中得出，结构的最大位移为5.103×10-2μm。最大应力出现在U形折叠梁上。

图13 z方向驱动结构整体变形和应力分布云图

从以上三个方向上的仿真结果中可以看出，振弦式陀螺驱动结构三个方向的重力敏感性都比较低。从位移上来说，振弦式陀螺受驱动方向和驱动垂直方向的重力影响较大，但变形小于1 μm；由于振弦式陀螺U形折叠梁厚度与宽度仿真优化后，U形折叠U形折叠梁结构沿z方向有足够的刚性，可以抵抗驱动内环驱动结构的重力，从而尽可能地降低振弦式陀螺受z方向重力加速度的影响。

4.2 振弦式陀螺谐响应分析

为更好的研究在振弦式陀螺驱动方向上不同频率的简谐载荷所引起的结构稳态响应，可以利用Ansys软件对振弦式陀螺驱动方向进行谐响应分析。对振弦式陀螺驱动框架单侧施加y方向简谐力载荷，取简谐力的幅值为10 mN。通过分析步骤：创建谐响应分析项目、施加载荷与约束、谐响应分析、结果后处理等，得到振弦式陀螺驱动结构y方向上的位移响应曲线和应变响应曲线，如图14所示。从驱动仿真结果中得出，驱动峰值频率为3 500 Hz，最大应力为132 kPa，幅值为9.27 μm。

图14 振弦式陀螺驱动结构位移响应和应变响应曲线

5 结束语

针对微陀螺高精度和微型化的发展趋势，依据振弦式陀螺的工作原理建立了圆壳体振弦式陀螺驱动模型；应用Ansys软件分析了圆壳体振弦式陀螺驱动中U形折叠梁结构参数以及内环驱动结构参数对驱动的影响，优化了圆壳体振弦式陀螺驱动结构并建立了振动响应仿真分析，优化结构表明，U形折叠梁宽度在1 mm,U形折叠梁厚度应在0.2～0.3 mm,内环驱动结构厚度应在1 mm,内环驱动结构宽度应在1 mm。从圆壳体振弦式陀螺振动响应仿真分析结果中表明:圆壳体振弦式陀螺受驱动方向和驱动垂直方向的重力影响较大但变形小于1 μm，优化后的U形折叠梁沿z方向有足够的刚性，可降低振弦式陀螺受z方向重力加速度的影响且从谐响应分析中得出驱动峰值频率为3 500 Hz，最大应力为132 kPa，幅值为9.27 μm。从而验证了圆壳体振弦式陀螺驱动模型的可行性，可以很好地控制振弦式陀螺框架驱动频率，优化圆壳体振弦式陀螺驱动结构,并为圆壳体振弦式陀螺实际产品试制研究奠定理论基础。