多域信息融合结合改进残差密集网络的轴承故障诊断
袁彩艳, 孙洁娣,2, 温江涛, 时培明, 闫盛楠,2
(1. 燕山大学 信息科学与工程学院,河北 秦皇岛 066004;2. 燕山大学 河北省信息传输与信号处理重点实验室,河北 秦皇岛 066004;3.燕山大学 河北省测试计量技术及仪器重点实验室,河北 秦皇岛 066004)
轴承是机械传动设备的关键部件,其故障所造成的损失和影响巨大,准确诊断和预警轴承故障意义重大[1]。
轴承工作过程中产生的振动蕴藏着丰富的运行信息,基于振动信号分析的数据驱动类故障诊断方法近年来得到快速发展,目前轴承故障诊断已全面进入智能化阶段。传统智能诊断方法主要包括数据特征提取、筛选及故障类别判断两步。特征提取中多采用时域、频域、时频域以及变换域[2-5]方法;故障类别判断则通常采用支持向量机、模糊推断及神经网络[6-8]等人工智能方法。但该类方法存在过度依赖复杂信号处理方法与诊断经验、人工特征提取主观性较强、不同应用的差异性较大、方法的通用性较差、分类采用的浅层模型无法从少量特征中获取全面反映复杂故障的信息等不足之处。
近年来,深度学习理论为解决传统方法的不足提供了有力支撑,滚动轴承故障诊断研究也进入新的阶段。学者们[9]构建了多种深度神经网络模型,采用深度学习方法对故障数据进行充分学习,挖掘大量数据内部隐藏的非线性关系,实现了对输入信号深层次特征的自适应提取,摆脱了对专业知识及诊断经验的过度依赖,更好地完成了故障特征提取与故障类型识别的协同处理。随着深度卷积网络(convolutional neural networks, CNN)在图像处理等领域显现出的巨大效果,学者们将其引入故障诊断领域并进行了深入研究。杨平等[10]针对滚动轴承故障,提出利用卷积胶囊网络对原始数据进行学习并实现故障分类。Lu 等[11]通过分段组合的方式将原始监测信号映射到二维矩阵中,经深度CNN网络自动学习高维特征表示,实现轴承的故障诊断。Ince等[12]提出利用一维CNN将特征提取和分类集成在一起,完成实时轴承故障诊断。Li等[13]提出集成深度神经网络和CNN相结合的轴承故障诊断模型,完成对轴承的故障诊断。Liu等[14]提出将卷积自编码和CNN相结合模型,前者用于原始信号的降噪,后者用于故障诊断。Chen等[15]提取齿轮箱各种故障状态信号的时、频域特征作为二维CNN网络的输入。
通过分析文献发现,当前基于深度神经网络的诊断方法多数都是通过构建复杂的网络模型、不断加深网络深度、层与层之间增加多种处理来实现诊断能力的提升,虽然提高了诊断准确率,但是随着网络层数的增加,此类深度结构也凸显出不少问题[16]:一方面容易导致梯度弥散或爆炸问题,使网络训练非常困难;另外,深度结构造成网络退化,训练时的损失不降反升,导致样本的训练误差增大,识别准确率降低;而且大规模深度网络的训练需要消耗大量的系统资源,这些问题都极大地限制了CNN在故障诊断领域的深入发展。最近,由He等[17]提出的残差网络简化了学习过程,增强了梯度传播,减轻了网络退化,通过在框架中引入快捷连接,允许数据信息直接在整个网络中传播,可以更好地提取出高层次的代表性特征。Peng等[18]提出将一维残差网络用于高速列车轮轴承故障诊断。雷亚国等[19]构建领域共享深度残差网络从源自不同机械装备的监测数据中提取迁移故障诊断特征,然后在深度残差网络的训练过程中施加领域适配正则项约束,形成深度迁移诊断模型。Zhang等[20]基于原始时域信号利用深度残差网络进行故障特征提取。
目前基于深度神经网络学习的数据驱动类故障诊断方法通过挖掘采集信号的深度信息从而判断故障类型。传感器监测的轴承振动信号通常是时域信号,为了能够更加凸显不同故障的差别,从多角度、多变换域对原始信号进行分析,更加有利于提高故障识别的准确率。学者们也研究了多种信号处理方法。Zhao等[21]利用快速傅里叶变换从一维振动信号中提取频率特征,再将其转化为二维频谱图作为残差网络的输入。Ma等[22]将振动信号进行小波后,每个子带系数作为残差网络的输入。Appana等[23]从振动信号中提取包络谱作为CNN的输入。Sadoughi等[24]在干草打包机滚动轴承故障诊断中,对振动信号进行谱峭度分析结果、包络分析和快速傅里叶变换结果组成了多通道特征作为CNN的输入。Wang等[25]研究了原始信号、快速傅里叶变换、连续小波变换和重构相空间对深度卷积网络性能的影响。Mao等[26]采用了由原始信号、希尔伯特-黄变换(Hilbert-Huang Transform,HHT)信号和傅里叶变换结果组成三通道数据。
不同变换域处理方法能够体现故障的差异性信息,本文提出一种多变换域处理方法,将原始信号、包络谱转换及离散余弦S变换的结果组成多通道信号,这样输入信号同时包含了时域、频域和时频域的多域信息,然后输入到残差密集模型中进行深度学习,更好的挖掘隐藏的故障信息。考虑到随着网络深度的增加,特征数量的增多,不同特征对信息的传递也存在差异,本文提出将学习到的特征进行注意力机制分配,实现特征的差异性划分,最后再利用softmax进行故障识别。
1 多通道变换域故障特征描述
滚动轴承原始振动信号仅含时域信息,为了诊断模型的输入尽可能包含综合信息,本文提出时域、频域和时频域信号组合的多变换域信号作为输入。
1.1 包络谱信息提取
当旋转的滚动轴承出现局部损伤时,会产生特定频率的振动,因此频谱分析一直是旋转机械振动信号分析中的重要内容。包络谱方法可以通过频率峰值提供故障部件的位置,并且能将高频共振解调为低频故障频率,可以为轴承故障诊断提供良好的频率分辨率[27]。本文包络谱计算方法基于希尔伯特变换,分为两步:
(1)该结构中希尔伯特变换
(1)
x(t)的解析信号的模为
(2)
(2)利用傅里叶变换得到包络谱
E(t)=|FT[xht(t)]|
(3)
研究表明,包络谱的振幅和频率峰值分别表示滚动轴承故障的严重程度和位置特性,因此可以提取出不同特征来对滚动轴承故障模式进行分类。
1.2 基于离散余弦S变换的信息描述
S变换继承了短时傅里叶变换和小波变换的优点,它使用频率可调、形状可变的窗函数,在时频双方面进行分解,具有时频聚焦性和时频多分辨率特点,但其冗余地在低频带与高频带存储了同等量的数据;离散正交S变换(discrete orthogonal stockwell transform, DOST)则致力于在时频域实现非冗余多分辨率处理,同时降低计算复杂度。DOST定义为[28]
(4)
用离散余弦变换(discrete cosine transform, DCT)代替公式离散傅里叶变换(discrete fourier transform, DFT)可以得到离线余弦S变换(discrete cosine stockwell transform,DCST)
(5)
利用二元分区对频率空间的划分进行调整。对于长度为2N的信号,每个分块频率的宽度定义为
n1=1
(6)
ni=2i-2, 2≤i≤N-1
(7)
研究表明,DCST的运算时间与消耗的内存较少,可以将轴承原始信号在时域中散布散乱的能量在频域中集中起来,并对轴承原始信号的低频带和高频带进行不同周期的采样。因此DCST可以对轴承原始信号的不同频率进行良好的检测和分析。
2 改进残差密集网络的故障特征学习
随着网络深度的增加,卷积神经网络的训练效果显著下降,而残差网络利用残差块内的跳跃连接将输入和输出进行逐元素相加,在不增加网络额外参数和计算量的情况下,大大加快了训练速度,改善了训练效果,并且可以解决由于层数加深带来的退化问题。因此本文提出将残差块作为轴承故障诊断的基本结构,并针对故障特征的差异提出将特征进行重要性区分,实现网络模型的改进,从而进一步提高故障诊断的识别准确率。
2.1 基于残差密集块的特征提取
为了有效地从多通道信号中学习故障特征,模型核心是构建一个深层次的一维网络,对信号特征进行逐层学习和抽象,但是简单地堆叠残差块组成链式结构,在深度网络的传输过程中很可能会丢失学习到的有效故障特征,本文提出将残差学习模块通过密集方式进行连接,构成如图1所示的残差密集结构。

图1 残差密集结构示意图Fig.1 Schematic of residual dense structure
图中残差密集块由多个卷积层、批量标准化、激活函数和快捷连接组成。它改善了通过网络的信息流,缓解了梯度消失问题;而且由于重用前一个卷积映射,避免了重新学习冗余特征,为后面层提供丰富的振动信号细节。
设x为网络输入,经过卷积1提取低级特征fea(x),fea(x)再经过卷积2提取到高级特征fea1(x),低级特征fea(x)和高级特征fea1(x)通过并联实现密集连接得到fea2(x),卷积3对输入X进行线性运算得到fea3(x),fea2(x)和fea3(x)通过串联形成剩余块结构。输出即为
y={σr[σr(w1*x+b1)*w2+b2∪σr(w1*x+b1)]}+
[σr(w3*x+b3)]
(8)
式中:w1,b1,w2,b2,w3,b3分别为卷积1、卷积2和卷积3待训练的参数;σr为激活函数Relu。
经过堆叠的多级残差密集块可以提取出大量的特征,但是这些特征并不是包含同等重要的故障信息,因此本文引入注意力机制对特征进行处理,实现对特征的差异性划分。
2.2 优化卷积结果的注意力机制
对于经残差密集网络学习后获得的大量特征,为了提高后续网络的分类效率,引入卷积注意力模块(convolutional block attention module,CBAM)[29]实现特征优化选择。CBAM主要通过串联通道注意力和空间注意力组成,通过对特征权重的重新分配以及定位实现自适应细化效果,CBAM结构如图2所示。

图2 CBAM结构图Fig.2 Schematic of CBAM
2.2.1 通道特征重要性区分
通道注意力图可以反映不同通道特征的重要性。计算过程如下:
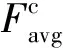
Mc(F)=σ{FMLP[Avgpool(F)]+FMLP[MaxPool(F)]}=
(9)
式中:W0∈Rc/r×c,W1∈Rc×c/r,W0后使用了Relu作为激活函数;σ为Sigmoid函数。为了表达的简洁,后文将通道注意力函数简写为fc。
2.2.2 重要位置特征的区分
空间注意力将注意力聚焦在特征的空间位置,计算过程如下:
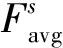
Ms(F′)=σ{f1*7{[Avgpool(F′);Maxpool(F′)]}}=
(10)
式中:σ为sigmoid函数;f1*7为大小为1*7的卷积。为了表达的简洁,后文将空间注意力计算函数简写为fs。
通过对特征进行通道及位置重要性的区分,实现后续处理中特征的差异性学习,提高学习效率。
3 本文提出的故障识别方法
针对深度卷积网络在提取特征方面的局限性,本文提出一种残差密集网络结合注意力机制的轴承故障诊断方法。本文构建的诊断网络包括多通道信息预处理、三级残差密集单元、带有CBAM的残差密集单元、平铺层、全连接层及softmax分类层。网络结构框架及信号处理过程如图3所示。
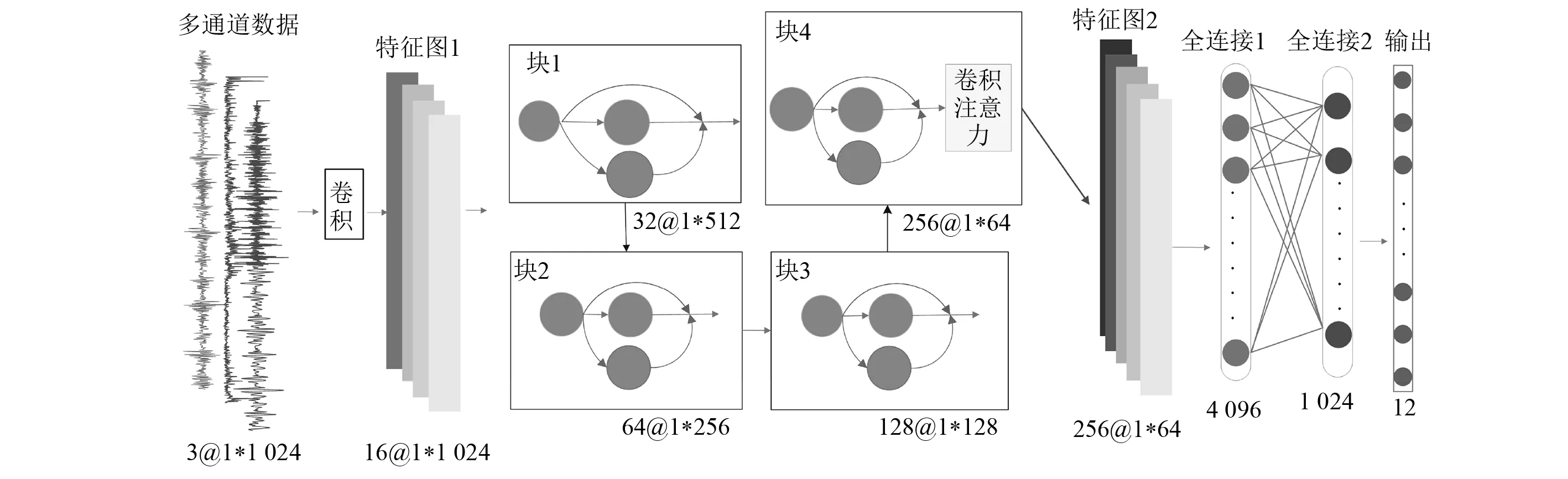
图3 本文方法的网络结构及处理框图Fig.3 Schematic of proposed method
该模型主体由残差密集块结合卷积注意力处理构成,实现从多通道数据中学习丰富的故障特征并对特征的权重进行划分。首先原始信号进行多域变换后与原始数据一起构成多通道信号作为输入;其次堆叠多级残差密集块,利用其强大的特征自学习能力从多通道信号中自适应提取故障特征;再次利用CBAM提高网络对关键特征的注意力;最后通过softmax完成分类,识别不同类型故障模式。
3.1 多通道数据输入
为了模型学习到的特征更加综合、全面,本文将时域、频域、时频域信息进行组合。首先将采集到的滚动轴承原始数据进行离散余弦S变换和包络谱提取,然后将变换结果与原始信号一起组合成多通道信号作为轴承故障诊断模型的输入。设组合信号为xi,利用步长为1,1*3大小的卷积核进行特征提取,可得浅层矢量特征
(11)
式中,θinp=(kinp,binp)为待训练参数。
3.2 基于CBAM的残差密集结构
CBAM原则上可以集合到任何CNN架构中,实现良好的注意力区分。在充分考虑其功能及作用的基础上,本文提出在最后一级残差密集单元中加入CBAM实现对大量特征的差异性划分。
(12)
式中,w1,b1,w2,b2,w3,b3分别为卷积1、卷积2和卷积3待训练的参数。
(13)
(14)
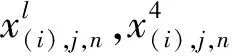
3.3 故障的分类识别
图4为本文轴承故障诊断的处理过程。
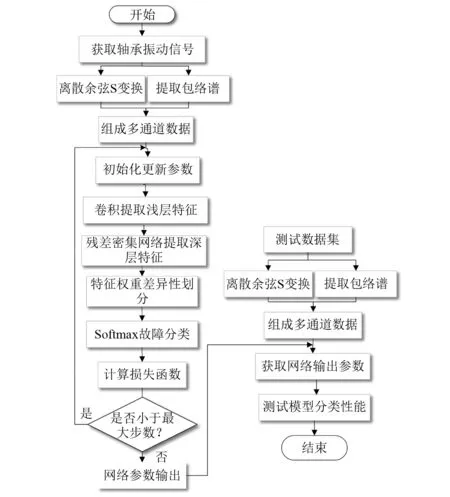
图4 本文方法处理过程Fig.4 Flowchart of the proposed method
网络在训练期间,根据梯度函数逐渐更新权重和偏差,反向传播算法用于监视学习过程并调整每层参数,计算每次网络迭代的误差。利用交叉熵损失函数对估计的概率分布和目标概率分布的误差进行评估。每次训练的交叉熵损失函数由前向计算得到,利用误差反向传播算法进行网络参数更新,直到最大训练步数,同时利用小批量随机梯度下降优化算法降低训练过程中交叉熵损失函数的值,使估计分布和目标分布越来越接近,从而逐步提高模型的预测精度。
4 试验结果与分析
4.1 美国凯斯西储大学数据集概况
本文数据集来自美国凯斯西储大学的轴承数据中心[30]。凯斯西储大学的测试设备包括两个电机,一个耦合器和其他设备,包含三个加速度计来收集振动数据,包括驱动端轴承壳体垂直方向的加速度计、风扇端轴承壳体垂直方向的加速度计以及电机支撑基板上的加速度计。其中驱动端轴承数据采样频率为12 kHz,模拟了四种状态类型包括正常状态,滚动体故障,内圈故障,外圈故障,其中滚动体,内圈,外圈又使用了不同损伤直径下(0.177 8 mm,0.355 6 mm,0.533 4 mm)下采样。
本文采用驱动端轴承壳体垂直方向的加速度计收集到的振动信号,将故障类型定义为内圈故障,并调整工作负载和损伤直径。在三种损伤直径(0.177 8 mm,0.355 6 mm,0.533 4 mm)和三种负载(0,735 W,1 470 W)下,构造了9类,再加上正常状态下三种负载(0,735 W, 1 470 W)下的工作状态,共构造了12类单故障(表示为0~11),详细描述如表1所示。
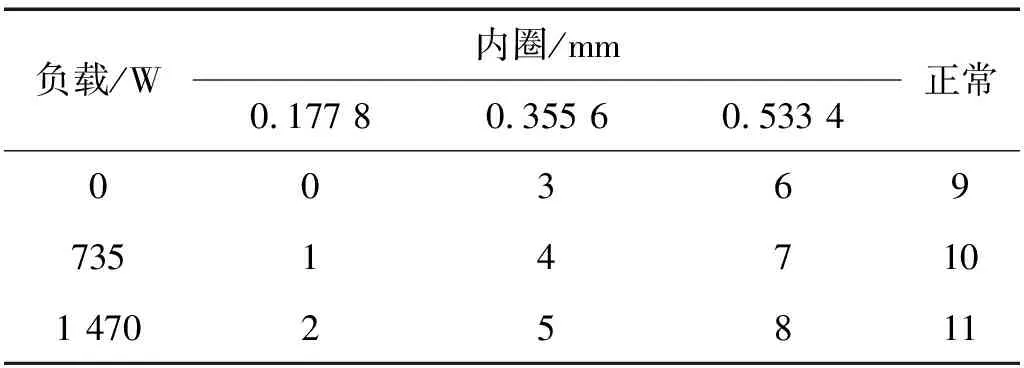
表1 数据集识别状态及分类标签
每类故障有100个样本,其中80%样本作为训练数据集。10%样本作为验证集,10%样本作为测试集,每个样本包含1 024点原始时间信号。
4.2 网络结构参数及诊断结果
在构造的数据集上按照本文方法进行多次数据处理,采用分类正确样本数与测试总样本数的比值来衡量总分类准确率,统计多次试验结果的平均识别准确率为99.24%。试验中诊断模型的具体参数如表2所示。
表2中卷积核大小为1*3,原因是1*3卷积核滤波器是中心,左/右等不同方向模式捕获的最小核,并且使用小卷积核滤波器会增加网络内部的非线性,从而使网络更具鉴别力。每增加一块残差密集块,特征映射的数目以2m(m=16)速率增加。每块残差密集块后都加一层步长为2的池化层来减小训练参数。为了避免数据的过度拟合,在全连接层F2后采用dropout,在网络中以0.5的比例进行分层训练。
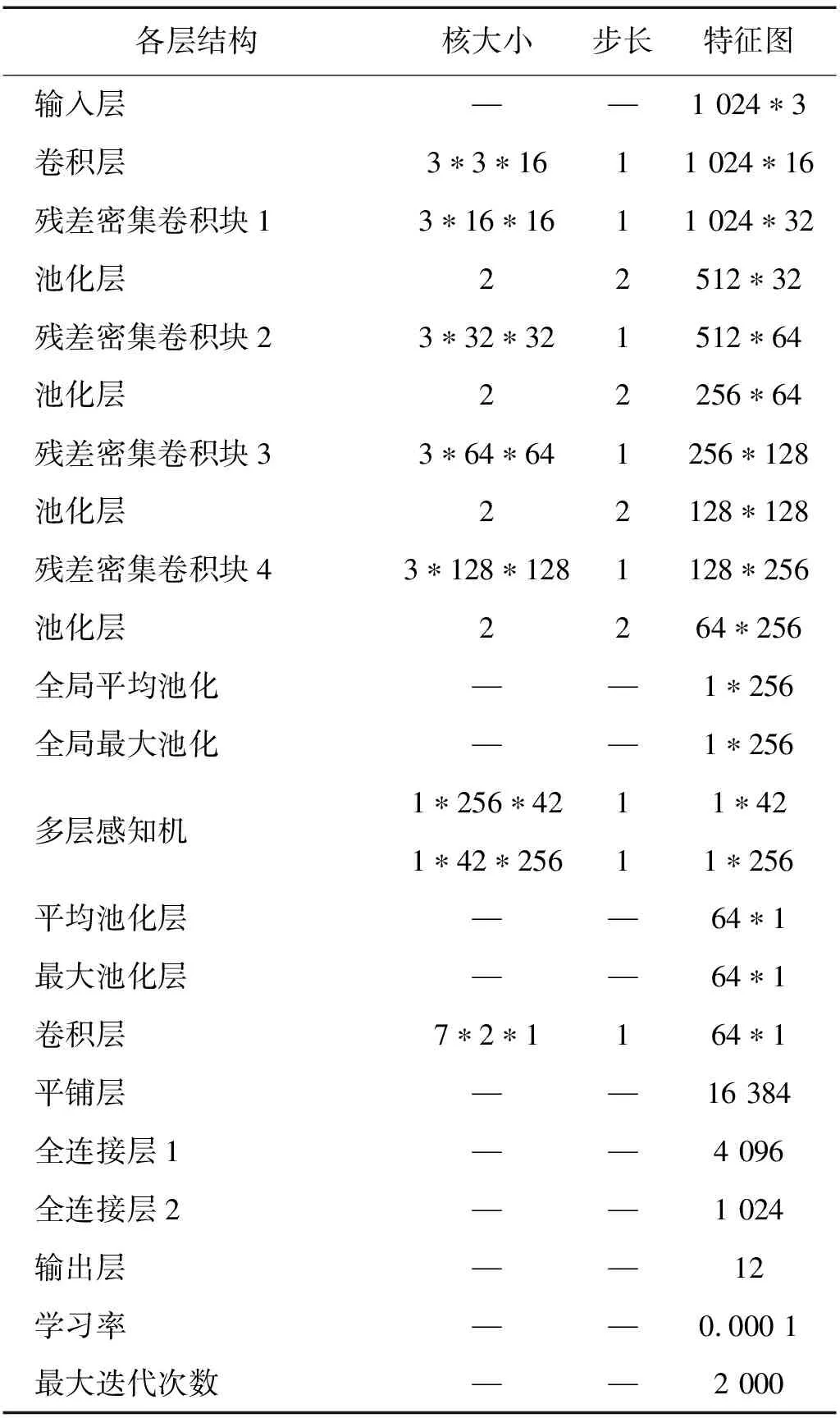
表2 本文网络参数表
本文方法某次分类结果的混淆矩阵,如图5所示。图5中横坐标为预测数据标签,纵坐标为真实数据标签,图中对角线表示正确分类的样本数量,其余每一块显示出错分为其他类别的样本数量。本文方法中分类准确率较高,只将少部分样本分类错误。
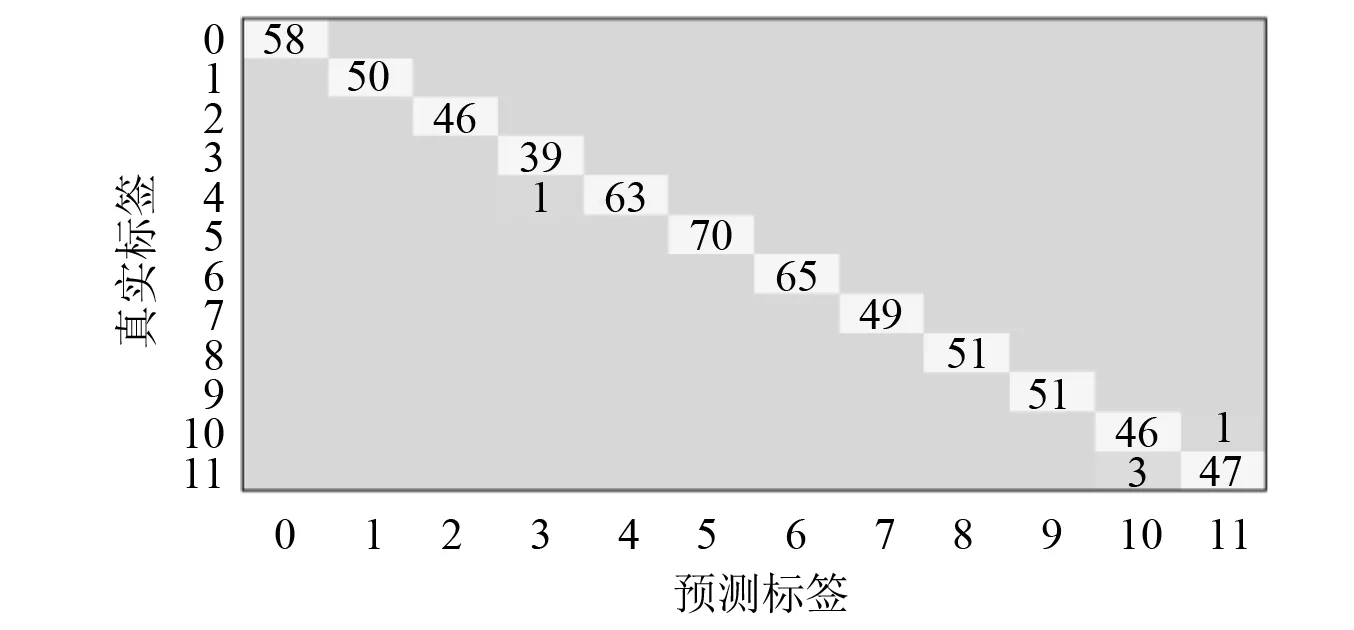
图5 某次分类结果统计的混淆矩阵Fig.5 Confusion matrix of statistics of a certain classification result
4.3 主要参数值的选择与其影响
构建的诊断网络中,选择合适的参数可以在保证较高分类正确率的前提下加快模型的训练速度,研究中发现网络的深度和批处理样本大小都会对故障诊断准确度和耗费时间产生较大影响,因此后文将对这些参数进行深入研究并分析其对诊断结果的影响。
4.3.1 网络深度的影响
理论上,网络结构越深误差越小,准确率越高。但与此同时网络复杂度也会随之增加,训练更困难。综合目前轴承诊断研究成果中通常采用的网络层数,并且考虑计算复杂度和实时故障检测的要求,本文设计了四种不同深度的残差密集结构,即残差密集卷积块个数分别为2,3,4,5,文中分别记为Ⅱ,Ⅲ,Ⅳ,Ⅴ级残差密集单元。为了减小随机因素的影响,每种方法的最终统计结果为10次重复试验结果的平均值。对不同深度的网络结构各自进行十次重复诊断试验,试验统计结果如图6所示。
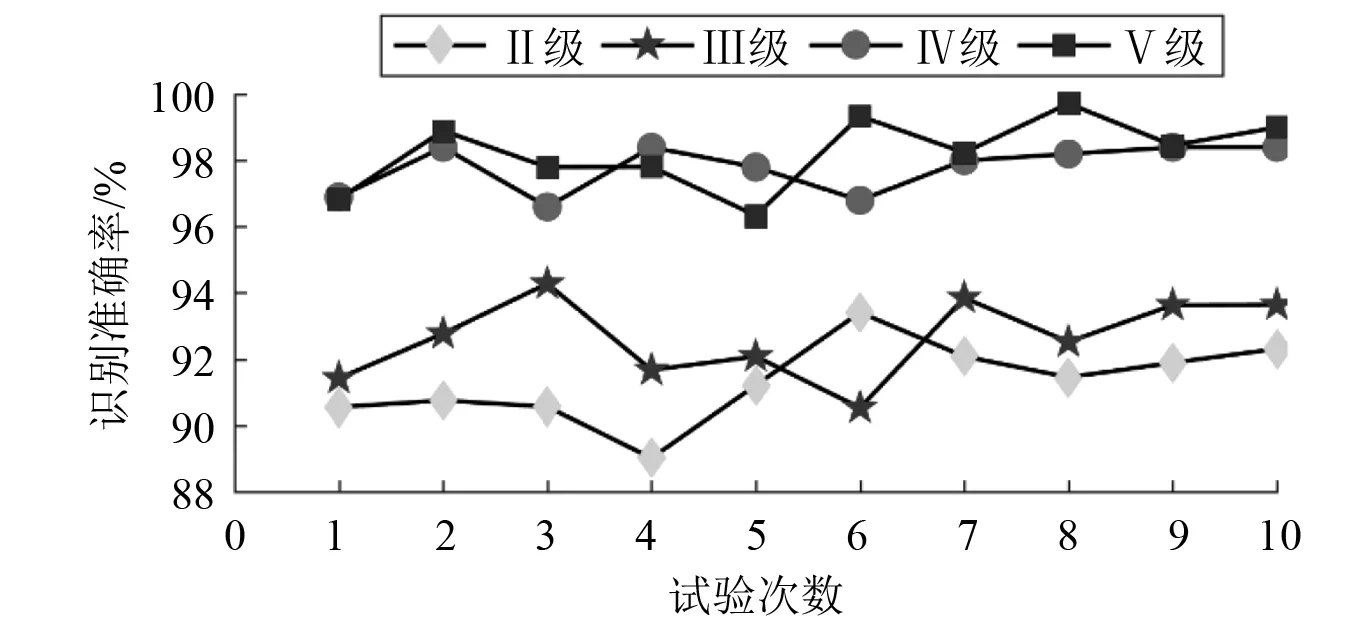
图6 不同深度网络的识别准确率Fig.6 Recognition accuracy in different depth networks
从图6中可以看出随着网络深度的增加,识别准确率也在增加,但是网络深度增加到一定程度,识别准确率并没有提高太多。下面分别从识别准确率、标准差、执行时间进行分析,统计结果如表3所示。
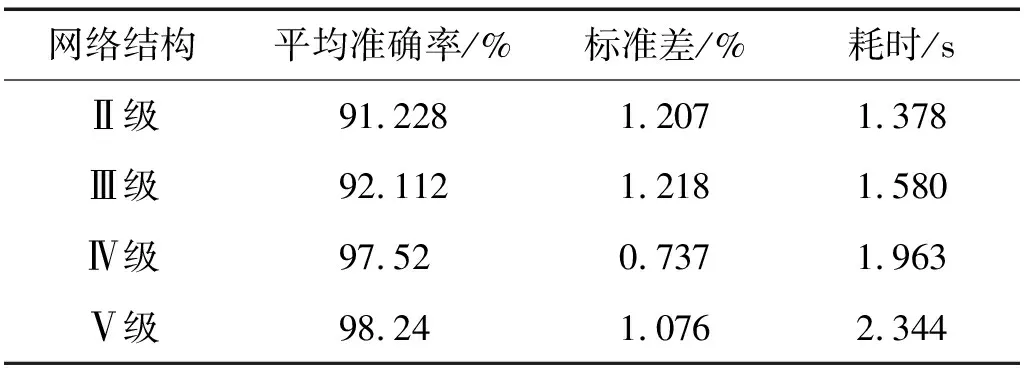
表3 不同网络结构的平均识别准确率统计结果
从平均准确率统计结果可以看出网络结构Ⅲ、Ⅳ级之间的平均准确率相差较大,而Ⅴ级比Ⅳ级的平均识别准确率仅高出0.72%;从执行一次批量样本所需时间统计结果可以看出,Ⅴ级所需时间较多且标准差与Ⅳ相比较大。综合分析,本文确定了Ⅳ级深度的残差密集网络实现对轴承的故障诊断。
4.3.2 批处理样本数目的影响
深度学习的训练样本数目较多,通常将训练样本划分成多个批次进行参数更新,样本规模较大时依然可以实现收敛。因此,每次批处理样本的数目对于诊断的准确率有重要意义。若批处理样本数目较少,则训练时间增加,且易陷入局部最优;若批样本数目较多,则无法保证参数的最佳优化方向。本文研究了批处理样本数目分别为16,32,64,128时对诊断准确率的影响,对不同批处理样本量各自进行10次重复试验,试验统计结果如图7所示。
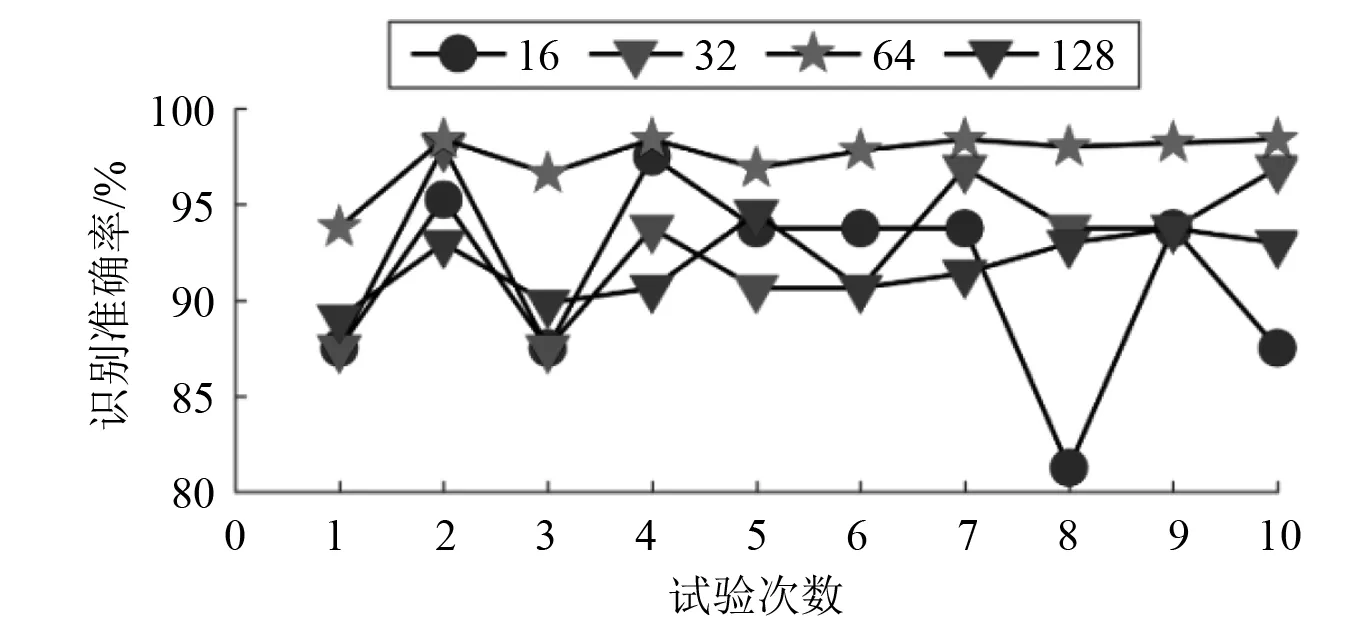
图7 不同批量样本数目识别准确率曲线Fig.7 Identification accuracy of different batch sizes
从图7中可以看出批处理样本数目为64时,识别准确率最高,且稳定性较好。表4为统计结果。
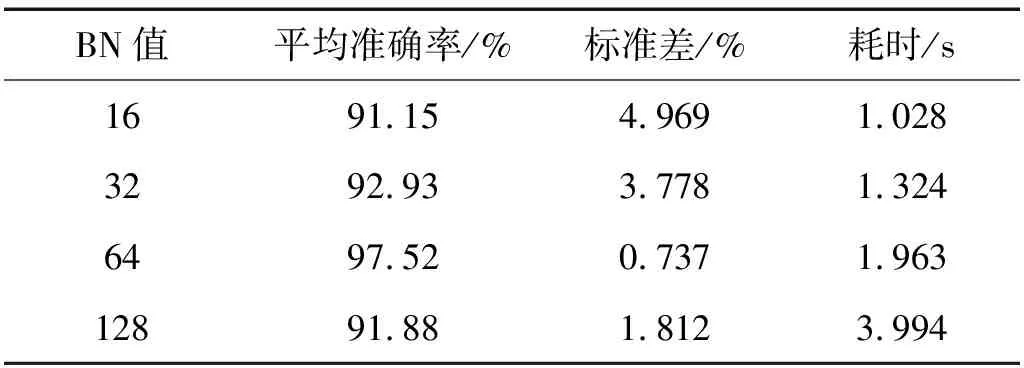
表4 不同批处理样本试验统计结果
由表4统计结果可以得出,批处理样本数目为64时损失最小的,且处理时间也在合理范围内。综上分析,本文中批处理样本数目设为64。
5 本文方法在数据集上的识别效果及分析
本文诊断方法可以分为两个主要步骤:多通道信号输入及具有注意力区分的残差密集结构。目前基于深度神经网络学习的故障诊断方法中,输入的多数为原始数据,本文为了从多方面挖掘故障信息,输入的是多种变换结果构成的数据;另一方面,识别结构采用了三级密集单元与一级卷积注意力机制结合的残差密集单元,这里将从不同输入数据及不同网络结构两方面进行诊断效果的比较。
5.1 不同输入数据的诊断结果比较
首先研究不同输入对故障识别效果的影响。图8为不同输入数据得到的识别准确率结果。
从图8可以看出,采用相同的诊断网络,本文提出的多域融合信息输入方法比单一数据输入的平均准确率高,并且本文方法的不同试验中识别准确率波动较小,有较好的稳定性,单次识别准确率的可信度高,并且平均损失也是最小。某次试验中每一类的识别准确率统计结果,如图9所示。
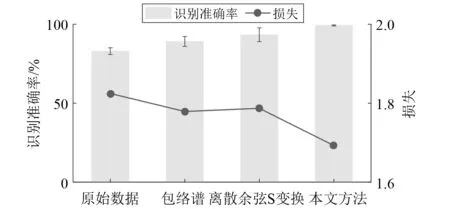
图8 不同输入数据的模型识别准确率Fig.8 Identification accuracy of different inputs
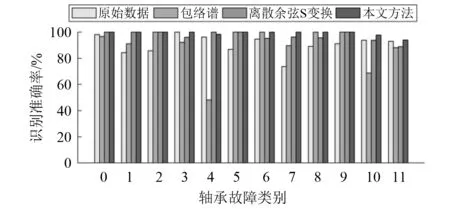
图9 某次试验不同输入数据的12类识别准确率对比Fig.9 Accuracy comparison of 12 classes input in an experiment
5.2 不同网络结构的诊断结果比较
本文构造的改进残差密集诊断网络主要包含多个残差密集单元及注意力机制操作,前文在确定网络结构时已研究了网络结构差异的影响,此处主要针对网络加入CBAM后及CBAM的位置对结果的影响,输入统一为多通道数据,比较的网络结构分为四类:
①四级残差密集单元(即表3中的Ⅳ级结构);
②一级密集残差单元+一级CBAM残差密集单元+二级残差密集单元(记为:1+1c+2级);
③二级密集残差单元+一级CBAM残差密集单元+一级残差密集单元(记为:2+1c+1级);
④本文方法(三级残差密集单元+一级CBAM残差密集单元)。
对上述网路结构分别进行10次重复试验,为了更加清晰地显示每个网络结构不同的分类效果,利用t-SNE对某次试验的分类结果进行可视化。结果如图10所示。
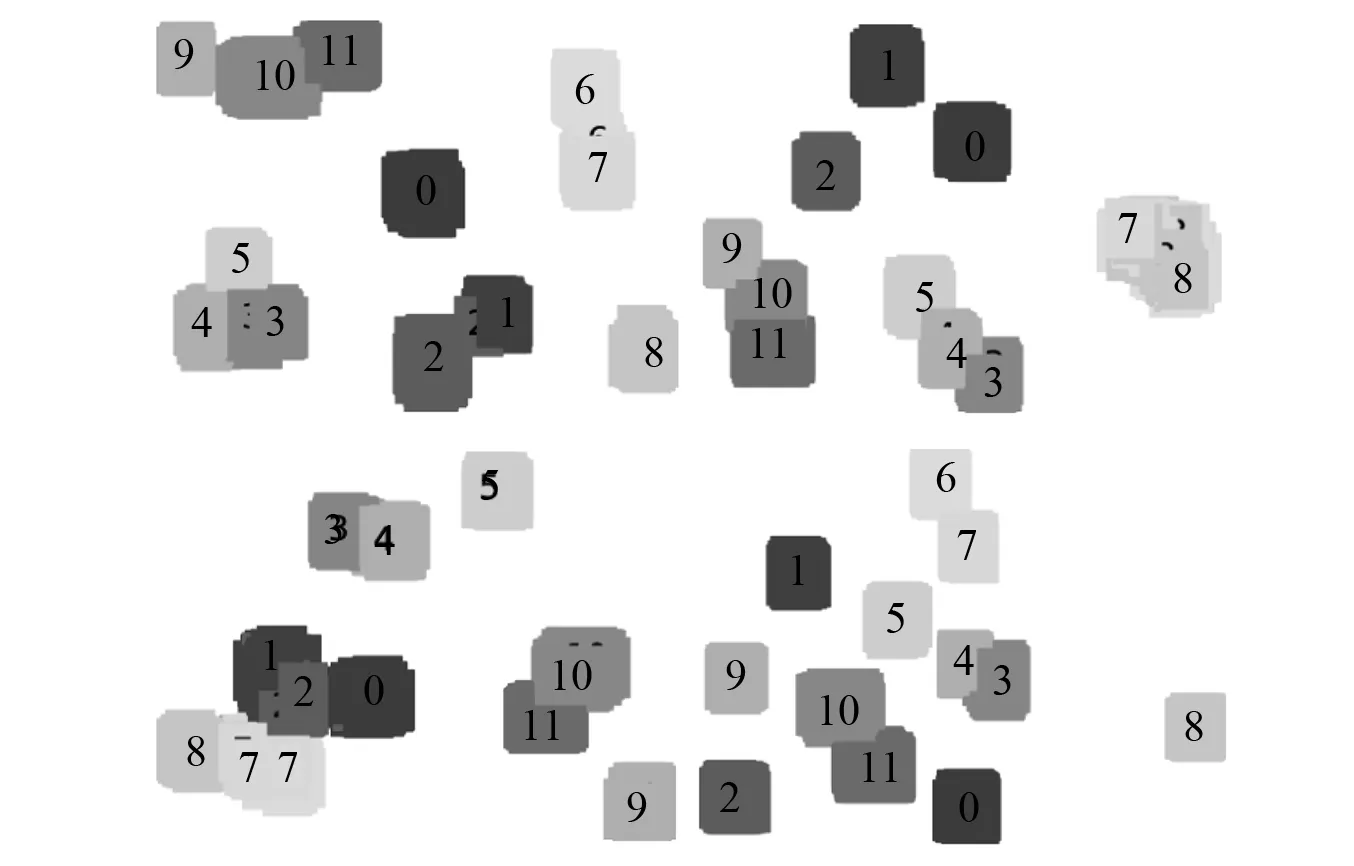
图10 方法①~方法④分类结果图Fig.10 Method ①-④ classification result
从图10可以看出方法②、方法③的分类效果较差,各个类别之间重叠较为严重,方法①分类效果较好,但不如方法④。因此可以得出将CBAM与第四块残差密集块结合后试验效果最佳。各个试验的统计结果见表5。

表5 不同模型结构试验统计结果
由表5可知本文结构与其他结构相比,平均识别准确率是最高的;多次试验结果的标准差最小。虽然处理时间稍长,但也在合理范围之内。某次试验中每一类的识别准确率统计结果,如图11所示。
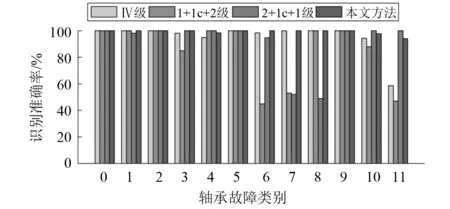
图11 某次试验不同模型12类识别准确率比较Fig.11 12 kinds of recognition accuracy with different models in an experiment
5.3 本文方法与常用方法的对比
本文在传统模型的基础上进行了改进,提出将原始时域信号及变换域信息构成多通道信号输入深度网络模型,并将CBAM引入到残差密集网络模型中,增加了数据的多样性并将提取的特征进行自适应细化,从而提高了轴承故障识别准确率。为了验证本文提出方法的有效性,将其与其他较为常用的深度网络模型的诊断效果进行比较。目前轴承故障诊断中较为常用的模型有卷积神经网络、卷积自编码,残差网络三种,其中卷积自编码的泛化性和鲁棒性较好。为了与本文方法的结构保持高度一致性,用于对比的各个模型的结构,如表6所示。

表6 常用深度学习模型结构表
每种方法各自进行10次重复试验得到的结果,如图12所示。
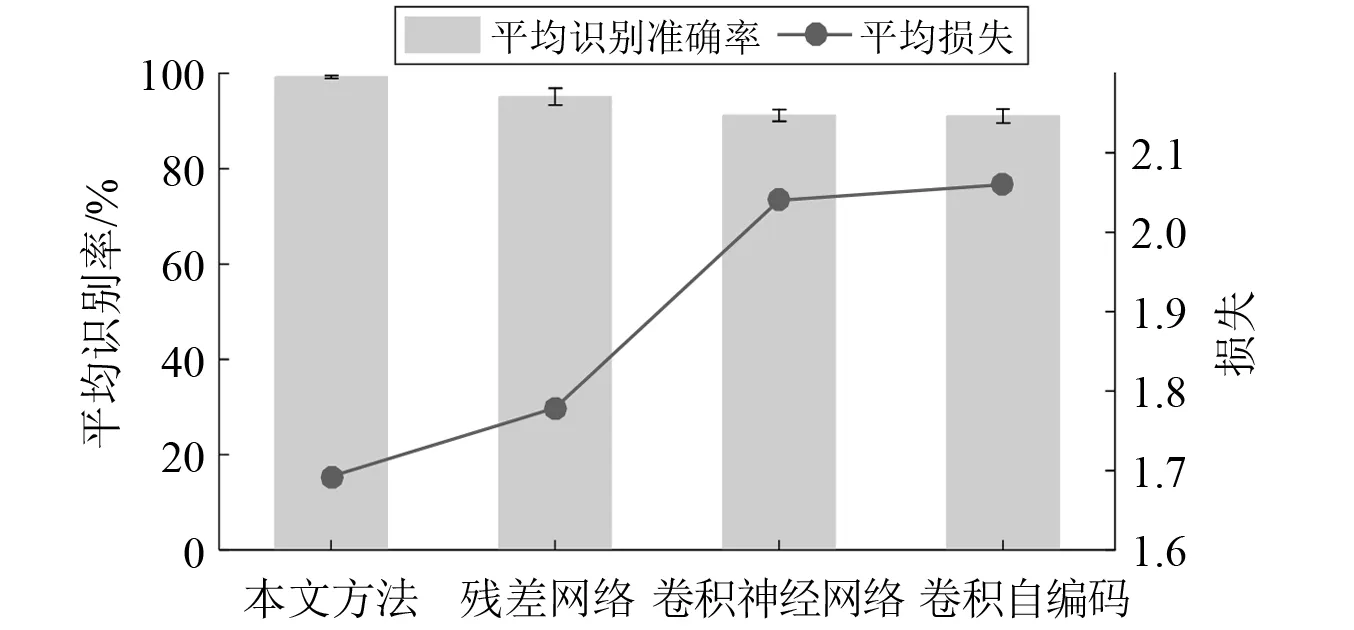
图12 与传统方法的识别准确率对比Fig.12 Accuracy comparison with common methods
观察到本文方法的平均准确率是最高的并且波动小,有较好的稳定性,单次识别准确率的可信度高。多次试验的各项统计结果见表7。
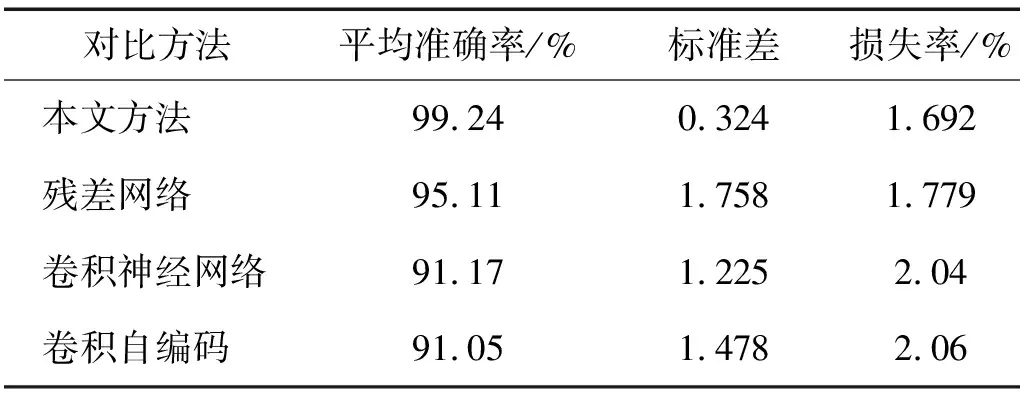
表7 与常用方法对比试验统计结果
6 结 论
针对原始轴承数据包含的信息较为单一、深度模型提取的特征对信息传递有差异的问题,本文提出将时域、频域、时频域多域融合信号作为输入,可以使输入包含较为全面的信息;卷积注意力处理可以实现对残差密集块提取的特征权重进行重要性区分。采用凯斯西储大学数据集验证了本文提出方法可以有效提高轴承故障诊断识别准确率。

