局域共振型隔振系统的低频振动特性分析

高晟耀 郭 彭 周奇郑

1.中国人民解放军92578部队，北京，1001612.海军工程大学兵器工程学院，武汉，430033

0 引言

振动是影响精密仪器测量精度的重要环境因素之一，精密仪器对环境振动都有着较为严格的要求，某些特殊的精密仪器对环境振动的要求甚至达到了微振动控制量级[1]。目前，精密仪器采用的减振措施对低频振动都比较敏感[2]，而低频振动又难以消除，因此，降低低频振动对精密仪器的影响具有重要意义。

精密仪器的振动控制一直是国内外学者研究的热点。目前常用的减振措施是在主系统与振源之间安装隔振装置或在主系统上布置若干吸振元器件[3]。文献[4]通过减振器的弹性变形和减振材料的阻尼耗能来降低设备的振动，并进行了试验验证。动力吸振器是一种不同于减振器的元器件，因其对低频振动简单有效的控制而备受关注。影响动力吸振器减振性能的因素有很多，吸振器的数量、布置方式、阻尼都会在一定程度上影响吸振器的减振性能。文献[5]针对单跨转子存在的振动问题，采用了多重动力吸振器的减振方式，研究了不同数量动力吸振器的抑振规律，发现在目标频段应用动力吸振器能够有效降低振动，且多重动力吸振器较单个动力吸振器减振性能好。近年来，局域共振[6-7]概念的提出为低频振动控制问题提供了新思路。局域共振型结构是一种人为构造的周期结构，其减振性能主要依赖于构成单元中微结构的局部共振。温激鸿等[8]构造了一种周期结构细直梁，并对其弹性波能带结构进行计算，发现在周期结构细直梁中存在局域共振带隙。王刚等[9]将局域共振机理与动力吸振器结合引入弯曲振动细直梁结构设计中，并研究了其弯曲波传播特性，得到了局域共振带隙，研究发现该带隙能够有效抑制振动的传递。SANGIULIANO等[10]构建了含不同长度、总附加质量和共振频率吸振器的有限局域共振梁，研究发现边界条件能够降低局域共振梁的减振性能。

本文在局域共振结构相关研究的基础上，区别于前人无限周期结构的研究思路，探究了有限周期结构下的振动特性。采用局域共振型结构的设计思想，在基体上周期布置若干单自由度吸振器，并将其分别划分为单振子、双振子、三振子局域共振元胞，运用模态叠加法计算不同元胞对设备振幅的影响以获得局域共振元胞的减振规律，并利用粒子群算法对振子的参数进行优化设计。

1 解析模型求解及验证

1.1 构建解析模型

精密仪器安装在基体上，基体在外力的作用下发生振动，必然会引起仪器的振动。以精密仪器安装在简支梁上为例，为了降低基体在外力作用下产生的低频振动对精密仪器的影响，在其表面均匀周期布置M个局域共振元胞，每个局域共振元胞中包含N个吸振器，建立图1所示的基体-隔振设备-吸振器系统的动力学模型。图1中设备的质量为m0，设备隔振器的刚度为k0，阻尼为c0，与隔振器相连的简支梁的长度为l，密度为ρ，横截面积为A，弹性模量为E。隔振设备与梁的连接点为x0，简支梁受到均布横向外力F(t)的作用。

图1 局域共振型隔振系统

图2所示为局域共振梁结构的单个周期元胞，图中，单个周期元胞内有N个动力吸振器，且每个吸振器中均包含阻尼元件，阻尼元件的存在不仅能有效拓宽减振频带还能一定程度上消耗主系统上的能量[11]。假设梁上第i个吸振器的位置坐标为xi，对应吸振器的质量、刚度和阻尼分别为mi、ki、ci。元胞的长度为a，元胞中N个动力吸振器将整个元胞分成N+1段，每段梁的长度记为aj，则吸振器位置关系可表述为

图2 局域共振梁结构的单个周期元胞

aj=xi+j-1-xi+j-2

(1)

1.2 解析模型求解

对于细长梁的低频振动，可以忽略梁的剪切变形以及梁截面绕中性轴转动惯量的影响，这种梁模型称为Bernoulli-Euler梁。局域共振型隔振系统可以被看成是一个连续离散耦合振动系统，由连续的简支梁和离散的吸振器以及隔振设备组成，根据其振动原理，可得到系统的耦合振动方程：

(2)

(3)

其中

(4)

研究简支梁受到横向外力F(t)=A0sinωt时设备的振动，根据梁的简支边界条件，由模态叠加法可得到梁的横向振动位移

(5)

Wm(x)=sin(mπx/l)

其中，m为简支梁的模态阶数；Wm(x)为简支梁在m阶模态下的振型函数；Wsm和Wcm分别为简支梁横向振动位移的正弦和余弦分量。

在耦合振动方程(式(2))等号两侧乘以简支梁在n阶模态下的振型函数sin(nπx/l)，并对x从0到l进行积分可得

(6)

将式(5)代入式(6)，并由简支梁的模态正交性可得

(7)

(8)

将式(7)和式(8)代入式(6)并与式(3)联合，取梁的前Q阶模态参与计算，并将耦合振动方程转化为矩阵形式：

Gq=F

(9)

其中，G为矩阵方程的系数矩阵；F为2(Q+MN+1)维的已知力向量，包含作用在梁上的横向外力；q为矩阵方程的待求未知向量，可表示为

(10)

其中，Ws=[Ws1Ws2…WsQ]T，Wc=[Wc1Wc2…WcQ]T，Us=[Us0Us1…UsMN]T，Uc=[Uc0Uc1…UcMN]T。

系数矩阵G可表示为

(11)

(12)

(13)

(14)

矩阵K1、K2、K3、K4被定义为刚度矩阵，其中包含了简支梁本身以及附加吸振器的质量和刚度对局域共振系统振动特性的影响，代表系统刚度成分对耦合振动的贡献。

(15)

(16)

(17)

矩阵C1、C2、C3、C4被定义为阻尼矩阵，其中包含了吸振器以及隔振设备的阻尼对局域共振系统振动特性的影响，代表系统的阻尼成分对耦合振动的贡献。

式(9)等号右侧已知力向量F可以进一步表述为

(18)

进而可以通过以下表达式计算得到在某激振频率下待求未知向量的解：

q=G-1F

(19)

假设简谐力的激振频率f=ω/(2π)，待求未知向量在各激振频率[f1f2…fe]下的解可以写为[q1q2…qe]，结合式(9)可以得到解矩阵的表达式如下：

(20)

结合上述推导过程，已知式(18)中Us和Uc：Us=[Us0Us1…UsMN]，Uc=[Uc0Uc1…

UcMN]T，则各激振频率下隔振设备的振幅可由下式计算得到：

(21)

其中，u为隔振设备在各激振频率下的振幅向量，各元素对应激振频率f。

1.3 解析结果验证

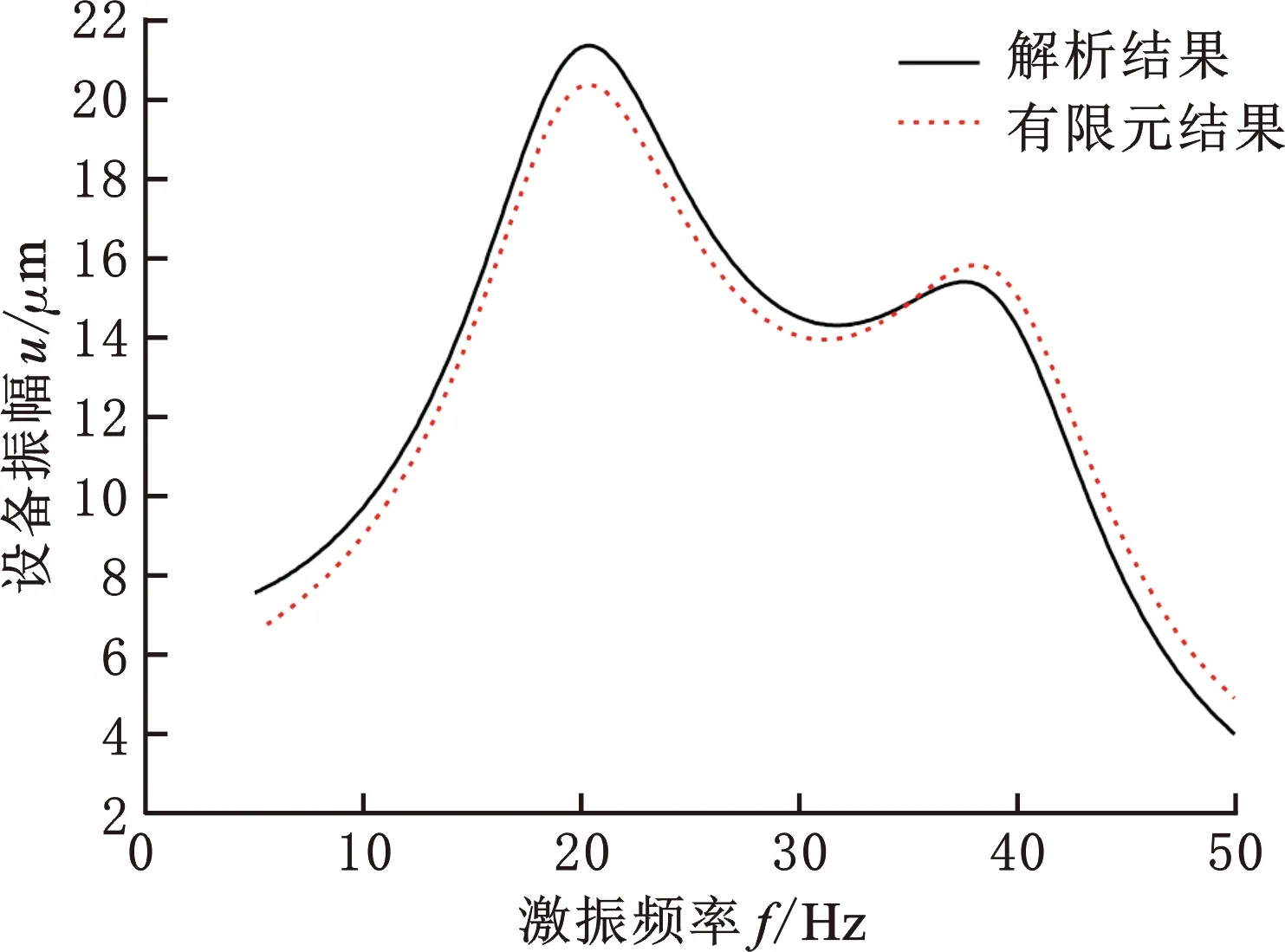
为进一步验证解析结果的有效性，本节利用有限元软件COMSOL对基体-隔振设备-吸振器系统的低频振动特性进行仿真，在只考虑梁的横向振动的情况下利用梁物理场(beam)构建出三维直线简化模型，并划分为50个边单元，利用集总机械系统物理场(lms)来模拟梁上振子以及隔振设备，基于模态叠加法取梁的前10阶模态参与计算。

考虑有限元模型中梁结构为简支梁，隔振设备安装在梁的中点位置，在简支梁表面施加横向均布载荷，载荷的幅值大小为1 N，激振力的频率f在5～50 Hz范围。取梁的初始计算参数如表1所示，其中ρ、E、υ分别为梁的密度、弹性模量、泊松比，l、B、H分别为梁的长度、宽度、厚度。取隔振设备质量m0=0.5 kg，刚度k0=9×103N/m，阻尼c0=46 N·s/m，隔振设备的固有频率为21.35 Hz。简支梁结构的固有频率可由下式计算得到

表1 简支梁的参数

(22)

其中，n为整数，表示简支梁的模态阶数。

(a) 无元胞

由图3a可以看出，图中出现了两个共振峰，第一个共振峰对应隔振设备的固有频率21.35 Hz，第二个共振峰对应简支梁的第一阶固有频率38.4 Hz。由图3b可知，在简支梁表面附加6个元胞之后出现了新的共振峰，共振峰的位置对应吸振器的固有频率17.08 Hz。为量化解析解和有限元解的一致性，现定义两者之间的相对误差ε=dm/xm，其中，dm为解析解和有限元解的绝对误差平均值，xm为解析解数据的平均值。计算可得在5～50 Hz范围内附加元胞前后解析解与有限元解之间的相对误差分别为4.39%和2.98%，解析结果和有限元结果的相对误差在理想范围内，验证了解析计算方法的有效性。

2 低频振动特性研究

隔振设备安装在简支梁上，在梁上周期布置若干吸振器形成局域共振型隔振系统，附加吸振器的数量和参数是控制隔振设备振动的重要因素。本节以单振子元胞为例，研究了吸振器的数量、刚度、质量以及阻尼对隔振设备低频振动特性的影响。梁与隔振设备的参数与1.3节算例保持一致，假设吸振器的初始计算参数为：质量比μ=0.16、固有频率比γ=0.8、阻尼比ζ=0.1。

2.1 附加振子对梁的振动特性的影响

以梁与隔振设备的耦合为例，对比分析设备与梁耦合前后梁的固有频率的变化。由式(21)可计算出未与隔振设备耦合时简支梁的前4阶固有频率，并利用有限元软件COMSOL计算出与隔振设备耦合后梁的前4阶固有频率，对比如表2所示。

表2 简支梁的固有频率

由表2可以看出，与耦合前相比，耦合后梁的各阶固有频率发生了移位，且在21.4 Hz能够发生共振，该频率对应的是隔振设备的固有频率，隔振设备中的阻尼成分也使得耦合后梁的各阶固有频率变成了复数形式。由表2对比可知，耦合作用对高频段梁的固有频率的影响小于对低频段梁的固有频率的影响。由此可知，附加振子与梁的耦合作用会对梁的振动特性产生影响，体现在梁的各阶固有频率发生了改变。

2.2 吸振器数量对隔振设备振动特性的影响

取吸振器的质量比μ=0.16、固有频率比γ=0.8、阻尼比ζ=0.1，通过计算5～50 Hz范围内隔振设备的振幅，分析梁上等间隔布置的吸振器的数量N对隔振设备振动特性的影响，如图4所示。

图4 不同吸振器数量下的设备振幅

将梁上布置吸振器前后隔振设备的振幅最大值分别记为Wmax0和Wmax，吸振器的减振效率可以表示为(Wmax0-Wmax)/Wmax0。由图4可知，在吸振器数量取5时减振性能最优，减振效率为11.34%，随着吸振器数量的增多隔振设备的幅值逐渐减小后又增大，减振效率从1.21%增至11.34%后又降至8.69%。由于吸振器与梁的耦合作用，在10～30 Hz频率范围内由原来的一个共振峰变为两个共振峰，新增的共振峰对应吸振器的固有频率。在给定吸振器的初始参数下，吸振器的数量会影响减振效率，但并不是吸振器数量越多减振效率越高，吸振器数量的选择还需结合实际需求。

2.3 吸振器质量比对隔振设备振动特性的影响

假定吸振器的固有频率比γ=0.8、阻尼比ζ=0.1，取吸振器数量N=6，通过计算5～50 Hz范围内隔振设备的振幅，分析梁上附加吸振器的质量比μ对隔振设备振动特性的影响，如图5所示。

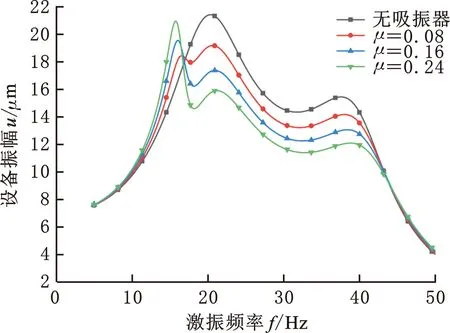
图5 不同吸振器质量比下的设备振幅

由图5可知，随着质量比的增大，吸振器的质量逐渐增大，吸振器与梁的耦合作用增强，在10～20 Hz频率范围内出现了新的共振峰。已知梁上未布置吸振器时设备振幅最大值为21.4 μm，吸振器的质量比μ分别取0.08、0.16、0.24时，对应的减振效率分别为10.46%、8.69%、2.18%。在目标频率范围内，随着吸振器质量比的增大，减振效率先升高后降低。在30～50 Hz频率范围内随着质量比的增大，吸振器的减振性能逐渐提高。

2.4 吸振器固有频率比对隔振设备振动特性的影响

假定吸振器的阻尼比ζ=0.1，取吸振器数量N=6，吸振器质量比μ=0.16，通过计算5～50 Hz范围内隔振设备的振幅，分析吸振器的固有频率比γ对隔振设备振动特性的影响，如图6所示。

图6 不同吸振器固有频率比下的设备振幅

由图6可知，在目标频段，随着吸振器固有频率比从0.4逐渐变化至0.83，吸振器固有频率增大，对应的共振峰逐渐向右偏移且峰值逐渐增大，隔振设备固有频率对应的共振峰值逐渐减小。在固有频率比取0.4和0.6时，吸振器固有频率对应的共振峰值远小于设备固有频率对应的共振峰值，此时随着固有频率比的增大，减振效率由2.71%增至8.69%。在固有频率比取0.8和0.83时，吸振器固有频率对应的共振峰值超过了设备固有频率对应的共振峰值，从而对减振效率产生主要影响，目标频段隔振设备的振幅最大值增大，减振效率又因此降至2.58%。总之，随着吸振器固有频率比的增大，减振效率在目标频段先升高后降低。

2.5 吸振器阻尼比对隔振设备振动特性的影响

取吸振器数量N=6，吸振器质量比μ=0.16，固有频率比γ=0.8，通过计算5～50 Hz范围内隔振设备的振幅，分析吸振器的阻尼比ζ对隔振设备振动特性的影响，如图7所示。

图7 不同吸振器阻尼比下的设备振幅

由图7可知，在10～30 Hz频率范围内，吸振器阻尼比取0.08和0.1时，出现了两个共振峰，分别对应着吸振器的固有频率和设备的固有频率，此时减振效率分别为4.43%和8.69%。吸振器阻尼比取0.18和0.2时，原来的两个共振峰变成了一个峰值较小且宽度较宽的共振峰，这是由于吸振器中阻尼成分的逐渐增大使得两个共振峰发生了叠加。由于在目标频段，设备振幅最大值减小，此时的减振效率增至12.20%。在30～50 Hz频率范围内，随着阻尼比的增大，隔振设备的振幅逐渐减小且振动趋于平缓。

3 吸振器的参数优化及分析

3.1 参数优化

假设简支梁以及隔振设备的各参数与1.3节算例一致，简支梁表面均匀附加吸振器总数N=6，各吸振器的质量比均为μ=0.16，在吸振器总数一定的情况下，将其分别划分为单振子、双振子、三振子元胞，取优化变量为吸振器的固有频率比γ和阻尼比ζ，取优化的目标函数为5～50 Hz范围内隔振设备的振动响应函数J，表示如下：

J=αWmax+βWavg

(23)

其中,Wmax、Wavg分别为目标频段隔振设备振幅最大值和平均值，α和β分别为分配给Wmax和Wavg的权重系数，取α=0.7，β=0.3。吸振器的固有频率在被控对象的固有频率附近时将有效减小被控对象的振动幅值[12]，这里确定优化变量的取值范围为0.5<γ<1.5,0.05<ζ<1.2。

取粒子群优化算法中学习因子的数值为2，初始权值wini=0.9，最终权值wend=0.4，并采用线性递减权值策略计算每次迭代时的惯性因子，即G=(wini-wend)(Gk-g)/Gk+wend，其中Gk和g分别表示最大迭代次数和当前迭代次数。在种群规模取N=100，最大迭代次数Gk=80时，对于单振子、双振子、三振子的优化均能达到收敛，以下讨论优化结果。

3.1.1单振子元胞

梁上均匀布置的6个吸振器划定为6个局域共振元胞，每个元胞包含1个振子。为验证优化结果的有效性，对比分析了附加单振子元胞优化前后的隔振设备在目标频率范围内的振幅。附加动力吸振器的初始参数如表3所示。

表3 单振子元胞初始参数

利用粒子群算法对元胞中振子的固有频率比和阻尼比进行优化，可得到优化后的相关参数为γ=0.7221，ζ=0.1321。将参数代入振动方程得到优化前后设备振动幅值，如图8所示。由图8可知，在10～30 Hz频率范围内，存在两个共振峰分别对应吸振器的固有频率和设备的固有频率。优化前，吸振器固有频率对应的共振峰值大于设备固有频率对应的共振峰值，前者对减振效率产生主要影响。优化后，吸振器固有频率对应的共振峰值明显降低，低于设备固有频率对应的共振峰值。对数据进一步处理，目标频段隔振设备振幅的最大值由优化前的19.5 μm降至优化后的18.7 μm，减振效率也由2.45%增至8.69%。

图8 单振子元胞优化前后设备振动图像

3.1.2双振子元胞

梁上均匀布置的6个吸振器划定为3个局域共振元胞，每个元胞中包含2个振子，假设元胞中振子的质量比分别为μ1、μ2，振子的固有频率比分别为γ1、γ2，振子的阻尼比分别为ζ1、ζ2，其中μ1=μ2=0.16。利用粒子群算法对振子的固有频率比和阻尼比进行优化，得到优化后的振子参数如表4所示。

表4 双振子元胞优化后参数

将优化后的参数代入振动方程得到隔振设备振动幅值变化曲线，如图9所示。由图9可知，双振子元胞比单振子元胞具有更好的减振性能，在目标频段，优化后的双振子元胞对应的隔振设备振幅最大值为17.5 μm，与优化后的单振子元胞的18.7 μm幅值相比有了明显改善。双振子元胞优化后的减振效率为18%，是单振子元胞优化后的减振效率的两倍有余。

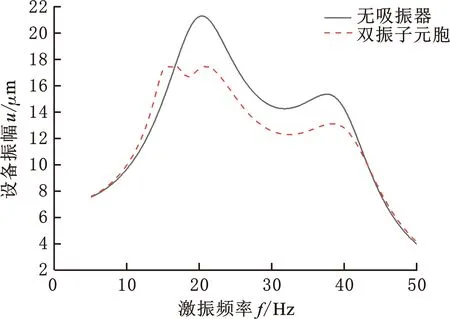
图9 双振子元胞优化后设备振动图像

3.1.3三振子元胞

梁上均匀布置的6个吸振器被分为2个元胞，每个元胞包含3个振子，假设每个元胞中振子的质量比分别为μ1、μ2、μ3，振子的固有频率比分别为γ1、γ2、γ3，振子的阻尼比分别为ζ1、ζ2、ζ3，其中μ1=μ2=μ3=0.16，利用粒子群算法对振子的固有频率比和阻尼比进行优化，优化后的参数如表5所示。

表5 三振子元胞优化后参数

将优化后的参数代入振动方程得到优化前后隔振设备振动幅值变化曲线，如图10所示。三振子元胞的减振性能与双振子元胞相近且稍优于双振子元胞，在10～30 Hz频率范围内出现了3个共振峰，这是设备以及元胞中不同固有频率的振子与梁耦合的结果，优化后的三振子元胞对应的隔振设备振幅最大值为17.47 μm，减振效率为18.3%。

图10 三振子元胞优化后设备振动图像

3.2 优化结果对比

单振子元胞的最大问题是减振频带较窄，不能适应变化较大的激振频率，而多振子元胞可以有效改善这个问题。对实验数据进一步处理，以包含不同振子的元胞优化前后的减振数据为依据，计算5～50 Hz范围内减振效率η的具体数值，如图11所示。可以看出，多振子元胞比单振子元胞的减振性能更好，进一步说明了局域共振元胞相比单一类型吸振器在振动控制上的优势。在动力吸振器发挥作用的整个频带内，三振子元胞的减振效率和双振子元胞的减振效率相近。在10～38 Hz频带内三振子、双振子元胞的减振效率均高于单振子元胞，且三振子、双振子、单振子元胞的减振效率分别为18.3%、18%和12.45%。为简化设计，在基体-隔振设备-吸振器系统动力学模型的局域共振型结构中选择双振子元胞设计即可。

图11 不同元胞的减振效率对比

4 结论

本文针对精密仪器低频振动问题，提出局域共振型结构的减振方式，构建基体-隔振设备-吸振器系统的动力学模型，计算耦合振动方程得到设备振幅的解析解，并利用有限元软件验证解析解的有效性。分析了吸振器各参数对减振性能的影响，在吸振器数目一定的情况下，将其划分为不同的局域共振元胞，并利用粒子群算法对元胞中振子的参数进行优化设计，分析优化后的减振性能，得到以下主要结论。

(1)在5～50 Hz范围内，附加元胞前后解析解与有限元解之间的相对误差分别为4.39%和2.98%，具有较高的吻合度，说明了解析计算方法的有效性。

(2)在目标频段内，按照单振子元胞吸振器初始计算参数，吸振器质量比、固有频率比、阻尼比分别在0.16、0.8、0.18附近取值时减振性能最优，减振效率分别为10.46%、8.69%、12.20%。

(3)局域共振元胞能够对低频振动进行有效控制。在目标频带范围内，取吸振器总数为6、质量比为0.16，元胞中包含振子的数量不同对隔振设备的减振效果也不同，三振子、双振子元胞优化后的减振效率相近，均在18%以上。

本文中的简支梁结构只是实际工程结构的简化模型，动力吸振器不仅代表一种弹簧质量模型，而且可以抽象为一般的弹性体模型，在结构上也可以向复杂化的方向推广以适应不同需求。