基于多源异构数据的数控铣削表面粗糙度预测方法
李聪波 龙 云 崔佳斌 赵希坤 赵 德
重庆大学机械传动国家重点实验室,重庆,400044
0 引言
随着经济高速发展与机械产品质量要求日益增高,提高机械产品质量是各国制造业激烈竞争的关键。表面粗糙度严重影响着产品的表面硬度、耐磨度、疲劳强度等性能[1],当重要零件在航空航天、精密制造等高端、复杂的环境中工作时,表面缺陷可能导致零件失效而造成巨大损失,因此表面粗糙度是衡量机械产品质量的重要指标。传统表面粗糙度检测方式是在加工完成后对工件进行检测,具有成本高、效率低等问题。在加工过程中实时预测工件的表面粗糙度,可为提高生产效率、降低生产成本以及提高产品质量提供支撑,因此研究数控铣削表面粗糙度预测技术具有重要意义。
机械加工过程中工件表面粗糙度的影响因素主要有刀具、工件材料、工艺参数及切削环境等[2],这些静态因素对表面粗糙度的影响具有复杂、非线性等特点。数据挖掘的参数建模方法具备强大的分析与决策能力,广泛应用于机械加工表面粗糙度预测并取得了较好的效果。LU等[3]将工艺参数和刀尖半径作为输入变量,运用支持向量回归方法建立表面粗糙度预测模型;AGRAWAL等[4]采用多元回归、随机森林等方法拟合AISI 4340钢车削过程中的表面粗糙度预测模型并揭示了表面粗糙度与工艺参数的关系;CHEN等[5]搭建嵌套人工神经网络,利用工艺参数预测表面粗糙度。随着传感器技术的发展,引入振动信号、力信号等动态数据来反映机械加工的动态变化可提升表面粗糙度预测模型的效果。如TANGJITSITCHAROEN等[6]考虑切削力、工艺参数和刀具直径,采用多元回归分析方法建立球头铣削加工过程表面粗糙度预测模型;GARCA PLAZA等[7]采用小波变换方法分析振动信号以实现表面粗糙度预测;朱俊江等[8]基于振动信号和神经网络预测数控铣削的工件表面粗糙度。上述表面粗糙度预测研究考虑的因素较少,均在固定工件或刀具的加工条件下建立模型且考虑的传感器种类较少,限制了模型的泛化性和精确性。此外,目前用于表面粗糙度建模的方法主要为经典统计方法[9]、支持向量回归[10-11]、人工神经网络[12-13]等传统方法。这些方法在构建模型的过程中,均采用人工提取的方式提取动态、静态数据的特征,导致传感器信号中大量的动态信息缺失,从而限制了表面粗糙度预测模型的精度。因此,运用自适应特征提取的方法获取动态数据中与表面粗糙度预测精度相关的重要特征,是提高预测精度的关键。
深度学习作为机器学习领域中的重要研究方向,具有强大的特征学习能力,为研究高维、非线性问题提供了新思路,其中,卷积神经网络(CNN)因具有学习效率高、准确度高的优点而在许多应用领域取得进展,如医疗[14]、故障诊断[15-16]等。同样,CNN也被用于表面粗糙度预测研究,如LIN等[17]基于振动信号建立了快速傅里叶变换-深度神经网络、快速傅里叶变换-长短期记忆网络和一维卷积神经网络(1D-CNN)三种表面粗糙度预测模型,通过对比分析表明1D-CNN有着很强的特征提取能力;PAN等[18]采用CNN自动提取振动信号特征以建立预测模型,实现了超声波椭圆振动切削过程的工件表面粗糙度在线预测。CNN的网络结构参数直接影响模型的预测性能,目前应用于表面粗糙度预测的CNN网络结构参数均是通过经验确定,这在较大程度上限制了预测模型的精度。粒子群优化(PSO)算法是由KENNEDY等[19]提出的一种适用于解决高维问题的全局优化算法,已成功应用在众多领域,因此通过PSO算法优化CNN关键网络结构参数可进一步提高模型预测精度。
综上所述,目前关于表面粗糙度预测的研究主要存在三个问题:①考虑的因素较少,均在固定工件或刀具的加工条件下建立表面粗糙度预测模型,模型建立后难以调整与修正,无法满足机械加工的动态需求;②使用的传感器种类较少,受传感器自身特性和实验环境干扰的影响较大,预测模型的鲁棒性和精度将受到较大限制;③采用CNN建立表面粗糙度预测模型时根据经验设置网络结构参数,在较大程度上限制了预测模型的精度。
为解决上述问题,本文综合考虑多源异构数据,即工艺参数、刀具直径及工件材料类别等静态数据和振动信号、力信号及功率信号等动态数据,采用PSO-CNN自适应提取动态数据特征,再通过浅层神经网络融合动态数据特征与人工提取的静态数据特征以建立表面粗糙度预测模型,最终提高表面粗糙度预测的泛化性与精确性。
1 数控铣削多源异构数据获取与特征提取
1.1 数控铣削多源异构数据获取和预处理
通信技术、传感器技术及云制造技术的飞速发展使得多源异构数据获取不再困难,这为融合多源异构数据建立数控铣削表面粗糙度预测模型提供了支撑。工艺参数、刀具直径及工件材料类别等静态数据决定了工件表面成形质量[20],对表面粗糙度影响十分显著。其中,工艺参数可通过PCMCIA网卡与Focas通信接口从数控系统读取,刀具直径与工件材料类别通过检索制造执行系统(manufacturing execution system,MES)的生产计划与工艺规划信息获取。同时,振动信号、力信号及功率信号等动态数据中蕴含着丰富的数控铣削动态信息,如刀具磨损等,因此采用振动传感器、力传感器及功率传感器和相应的通信协议进行采集。此外,表面粗糙度则通过白光干涉仪扫描工件表面形貌特征并用Gwyddion软件计算得到。最后将获取的数据集成到电脑进行预处理并存储,为建立表面粗糙度预测模型提供准备。数控铣削多源异构数据获取如图1所示。

图1 数控铣削多源异构数据获取
数控铣削车间环境复杂恶劣且铣削过程的动态、静态数据耦合性强、数据量大,这对原始数据的采集与转换造成了严重影响,如车间噪声、操作失误、采集软件运行出错等将导致数据异常、数据缺失等问题。直接使用原始数据建立表面粗糙度预测模型将使模型预测效果差、运行效率低。本文采用DataWrangler软件来清洗数控铣削的原始多源异构数据,纠正数据异常与缺失,为建立数控铣削表面粗糙度预测模型提供准确、有效的数据支持。
1.2 数控铣削多源异构数据特征提取
本文综合考虑多源异构数据建立表面粗糙度预测模型,输入变量为X={x1,x2,x3,x4,x5,x6,x7,x8,x9|主轴转速(n),进给速度(fv),切削深度(ap),切削宽度(ae),刀具直径(dt),工件材料(wm),振动信号(V),功率信号(P),力信号(F)}。针对动态数据,采用PSO-CNN自适应提取特征为建立模型提供全面、准确的动态数据特征,以提高模型预测的精确性。静态数据维度小,PSO-CNN不适用,因此人工选取变量{x1,x2,x3,x4|n,fv,ap,ae}作为工艺参数特征,选取变量{x5|dt}作为刀具特征,选取变量{x6|wm}作为工件材料特征。
此外,工件材料{x6|wm}是表示类别的离散型数据,采用独热编码(one-hot encoding)将其转化为数值型数据,运用N位状态寄存器对N种状态进行编码,当表示第i种状态时,寄存器第i位标记为1,其他位标记为0。因此,本文工件材料编码后为x6={(1 0 0), (0 1 0), (0 0 1)|Q235,45钢,6061铝合金}。{x1,x2,x3,x4,x5,x7,x8,x9|n,fv,ap,ae,dt,V,P,F}为连续型数据,采用Z-score方式将其标准化为量纲一数据,使得数据服从均值为0、标准差为1的标准正态分布,消除了变量间量纲和取值范围差异对数据分析结果的影响,计算如下:
(1)
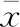
2 基于多源异构数据的数控铣削表面粗糙度预测模型
2.1 考虑多源异构数据的卷积神经网络模型
针对数控铣削过程的振动信号、力信号与功率信号,本文采用1D-CNN直接处理原始数据。1D-CNN的结构包括特征提取和回归两部分,其中,特征提取部分由输入层、卷积层及池化层组成,并以卷积和池化交替进行特征提取。卷积核按指定步长在原始信号上进行卷积运算,将振动信号、力信号与功率信号简化为稀疏特征映射。卷积过程如下所示:
(2)

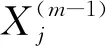
(3)

卷积运算后,需应用线性整流函数(rectified linear unit, ReLU)对卷积层输出数据进行处理,计算过程如下:
f(x)=max(0,x)
(4)
式中,x为卷积层的输出。
本文选择最大池化运算作为池化层以减少数据维度和网络参数,可加快计算速度,防止模型过拟合,提高模型的泛化性,计算过程如下:
(5)

1D-CNN的回归部分由全连接层、浅层神经网络及输出层组成,采用浅层神经网络融合CNN提取的动态数据特征与人工提取的静态数据特征拟合出表面粗糙度预测模型。基于多源异构数据的卷积神经网络结构如图2所示。其中,XM,N表示卷积层的输入数据有M个通道和N个数据点;ZM,T表示池化层的输出数据有M个通道和T个数据点。

图2 基于多源异构数据的卷积神经网络结构
2.2 基于PSO算法优化CNN
在使用CNN时,其网络参数往往通过人工试错的方式确定,该方式效率低且难以达到最优,有较大的优化空间。CNN各卷积层的卷积核个数决定了数据的特征表达,因此是优化CNN时的重要对象,如曹继平等[21]采用PSO算法优化CNN各卷积层的卷积核个数等参数,使得轴承故障分类精度大幅提高。在调试本文搭建的CNN时发现,各卷积层的卷积核个数、全连接层节点数及浅层神经网络隐藏层的神经元个数Q={q1,q2,…,qD}对模型预测精度影响显著,故本文采用PSO算法以模型的均方根误差(RMSE)为目标,以Q为优化变量,得到PSO-CNN。
PSO算法首先初始化规模为N的随机解,任意一组解为一个粒子,各个粒子在解空间中追随最优粒子搜寻最优值。粒子通过种群迭代找到个体最优值Upbest与群体最优值Ugbest并更新粒子的速度和位置,更新过程如下:
(6)
(7)

卷积核个数、全连接层节点数及隐藏层神经元个数均为整数,粒子群位置参数w、c1、c2、r1、r2可能为小数,将导致粒子位置为小数,故在粒子位置更新后向上取整。PSO算法的粒子每更新一次,CNN将训练一个模型,比较各个粒子模型的预测精度并更新粒子,直到RMSE达到要求或迭代次数达到预定值。设N为种群数量,D为粒子维度,fitl为第l个粒子的适应度值(即RMSE),fitgbest为群体初始最优适应度值,M为最大迭代次数,ks为卷积核大小、ppool为池化层参数,e为训练轮次,b为数据批次大小,基于PSO算法优化CNN的流程如下所示:
设置:N,d,fitgbest,M,w,c1,c2,r1,r2;
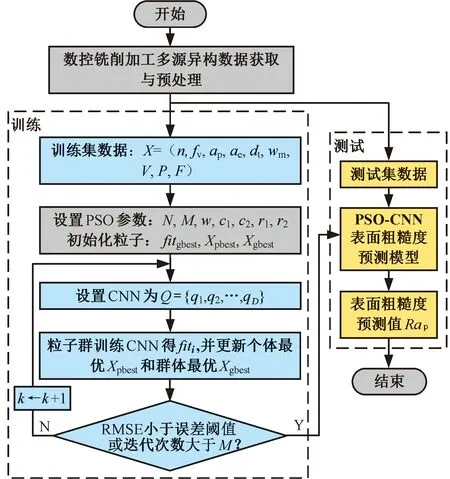
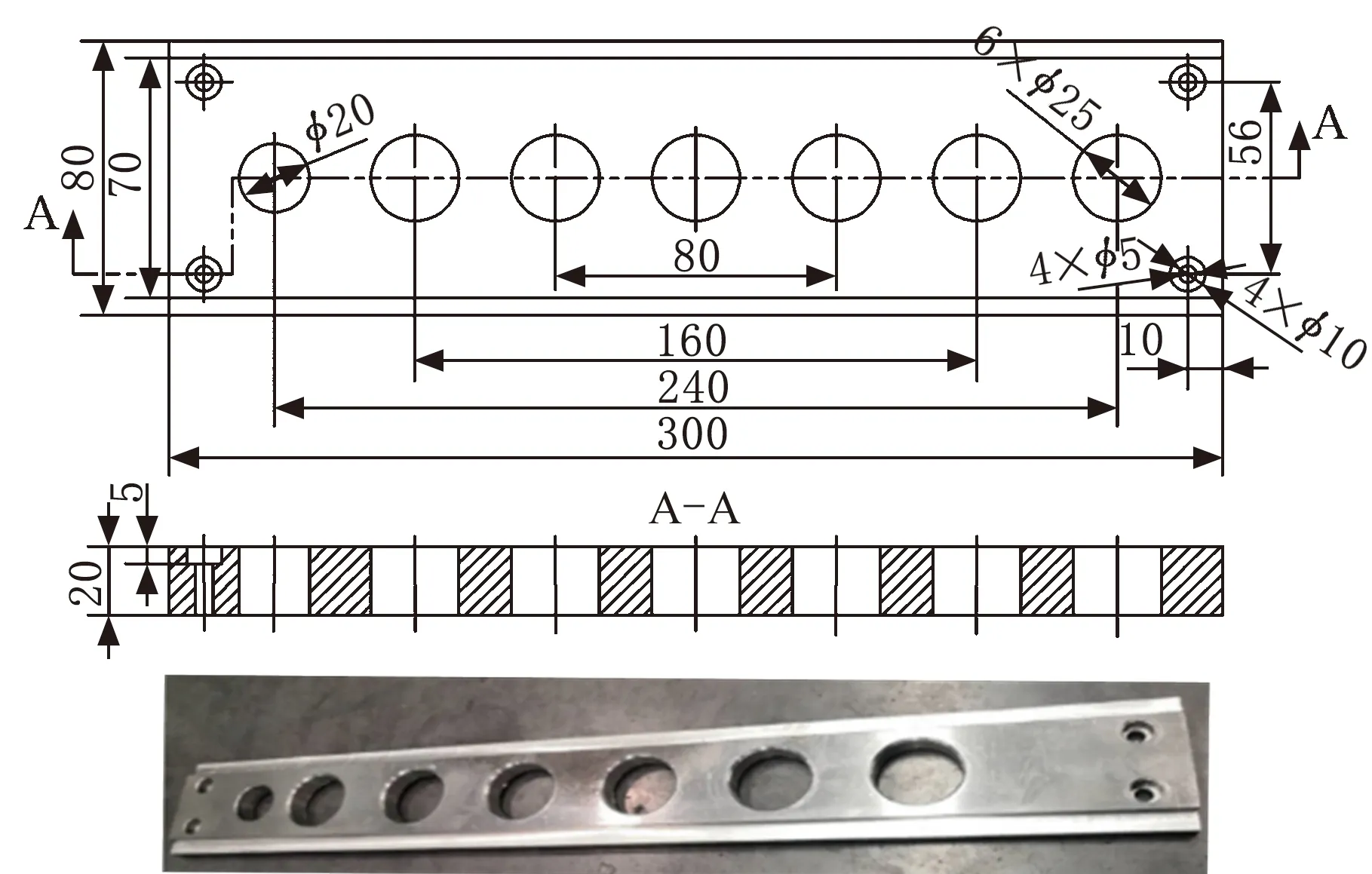
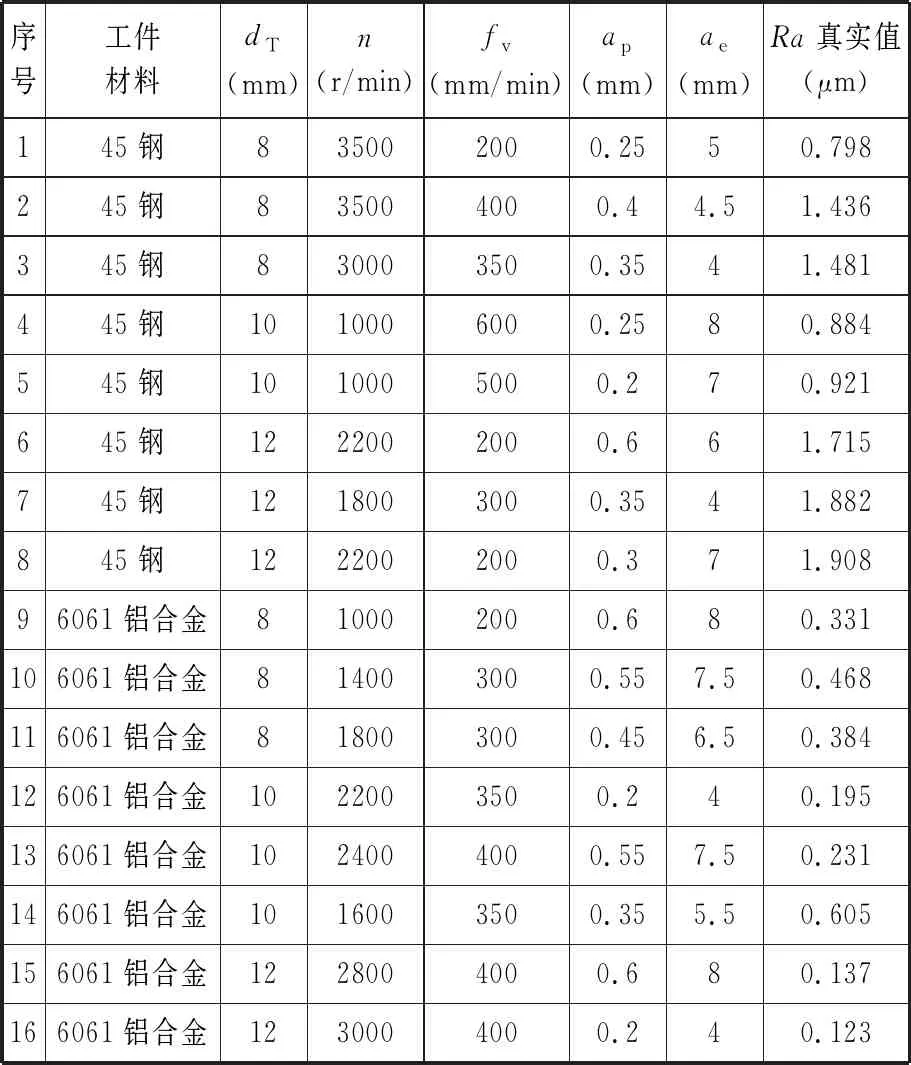
1: forl=0;l 2: forj=0;j 3: 初始化粒子位置Ulj、粒子速度Vlj 4: end for 5: 设置粒子最优解Upbest(l)=Ul 6: 执行函数CNN Solution(Ul),得fitpbest(l)=fitl 7: if (fitpbest(l)优于fitgbest) then 8: 更新群体最优适应度值fitgbest=fitpbest(l) 9: 更新群体最优解Ugbest=Ul 10: end for 11: fort=0;t 12: forl=0;l 13: 执行函数CNN Solution(Ul),得fitl 14: if (fitl优于fitpbest(l)) then 15: 更新Upbest(l)和fitpbest(l) 16: if (fitpbest(l)优于fitgbest) then 17: 更新Ugbest和fitgbest 18: end for 19: forl=0;l 20:Vl=wVl+c1r1(Upbest(l)-Ul)+c2r2(Ugbest-Ul) 21:Ul=Ul+Vl 22: end for 23: end for 24: 输出Ugbest和fitgbest CNN适应度函数如下所示: 1: function CNN Solution(Ul) 2: 设置:Q={q1,q2,…,qD}=Ul,ks,ppool,e,b; 3: 训练CNN,得到Ra预测模型 4: 在测试集上预测,得到Ra的预测值y* 6: 输出适应度值fitl 7: end function 本文基于多源异构数据建立泛化性强和精确度高的数控铣削加工表面粗糙度预测模型。首先获取数控铣削过程中的工艺参数、工件材料类别、刀具直径等静态数据和振动信号、力信号、功率信号等动态数据组成的多源异构数据集并进行预处理。在训练集上采用CNN建立表面粗糙度预测模型,并使用PSO算法优化CNN网络结构参数得到PSO-CNN,在测试集上运用PSO-CNN表面粗糙度预测模型进行测试并得到表面粗糙度预测值。训练与测试流程如图3所示。 图3 表面粗糙度预测模型训练与测试流程 与传统表面粗糙度建模方法相比,上述基于多源异构数据和PSO-CNN的表面粗糙度预测建模流程的优势主要体现在两个方面:一方面,本文考虑多种材料、多种直径刀具及多种传感器信号等多源异构数据建立模型,使模型泛化性更强、精度更高;另一方面,针对动态数据,本文在CNN自动提取特征的基础上使用PSO算法优化CNN网络参数,实现动态数据特征自适应提取,与传统的人工提取特征相比,将最大程度地提取出完整有效的特征,使得模型预测更加准确。 均方根误差(RMSE)可以用来量化预测值与观测值的绝对误差,故本文使用RMSE作为CNN的损失函数: (8) 同时,在使用PSO算法优化CNN网络结构参数的过程中,以RMSE作为优化目标。此外,平均绝对值误差(MAE)也是量化预测值与观测值的绝对误差的指标,决定系数R2可用来评价模型的可靠度,取值范围为[0,1],MAE和R2的计算公式如下: (9) (10) 故本文综合eRMSE、eMAE、R23个指标对表面粗糙度预测模型进行评估,其中,eRMSE、eMAE值越小说明预测值与观测值越接近,R2值越接近1说明模型预测精度越高[22]。 基于本文提出方法建立数控铣削表面粗糙度预测模型需要采集数控铣削过程中的多源异构数据,因此,在某数控铣削加工车间的VGC1500立式数控加工中心上开展数控铣削实验。详细信息见表1。 表1 机床参数 本文在开展数控铣削实验时,具体使用型号为E4A04050,直径分别为8 mm、10 mm、12 mm的刀具分别对Q235、45钢、6061铝合金材料进行平面铣削,将实验计划录入MES系统。同时,采集铣削过程中的多源异构数据,其中工艺参数通过PCMCIA网卡与Focas通信接口直接从VGC1500加工中心的FANUC数控系统读取获得,刀具、工件材料信息直接从MES检索获得。此外,使用3个PCB352C03单轴加速度振动传感器和3通道NI-9234振动输入模块采集X、Y、Z方向的振动信号,采集频率设为5120 Hz;使用Kistler9257B三向测力仪采集X、Y、Z方向的力信号,采集频率设为5120 Hz;将功率传感器的采集频率设为5120 Hz以获取主轴、X方向进给轴、Y方向进给轴功率信号。最后,使用MFT-3000高集成多功能摩擦磨损试验机扫描已加工工件的表面形貌特征并采用Gwyddion软件计算得到工件的表面粗糙度Ra,实验设备如图4所示。 图4 实验设备 3.2.1数据准备 本文通过不同工艺参数、刀具直径、工件材料组合开展150组数控铣削实验,在每组工艺参数下进行平面铣削时,采集10 s的动态信号,即以5120 Hz的采集频率在10 s内获取51 200个数据点。首先,将采集的振动信号、力信号及功率信号等多源异构数据的原始数据保存为CSV格式文件并导入DataWrangler软件中。然后,借助DataWrangler强大的操作智能推荐,删除原始数据中的空值,针对原始数据中的奇异值,先执行删除操作,再利用填充功能将其填充为合理值。最后,截取3种信号在同一时段的2048个数据点用于建立表面粗糙度预测模型。本文实验获取了150组数据,其中120组数据作为训练集,30组数据作为测试集,部分实验结果如表2所示。 表2 部分实验结果 3.2.2建立模型 基于准备好的实验数据建立数控铣削表面粗糙度预测模型。首先,针对静态数据,采用人工提取特征,针对动态数据,搭建CNN从每条动态数据的2048个数据点中自动提取有效特征,本文采用的卷积神经网络结构如图5所示,包含输入层、卷积层C1、池化层P2、卷积层C3、池化层P4、卷积层C5、池化层P6、全连接层F7、浅层神经网络隐藏层H8和输出层。 图5 本文的卷积神经网络结构 本文运用PSO算法以卷积层C1、C3、C5的卷积核个数q1、q2、q3,全连接层F7的节点个数q4、隐藏层H8的神经元个数q5为优化变量,以表面粗糙度预测模型的RMSE为优化变量对CNN进行优化,进而提高模型的预测精度,PSO的相关参数如表3所示。 表3 算法主要参数 本文采用Dell Precision 3640计算机、RTX 2080Ti显卡及64 GB运行内存,在Windows 10 64位操作系统、Keras及TensorFlow-GPU环境下运行PSO算法优化CNN以训练表面粗糙度预测模型。在训练模型阶段,设置好粒子群初始值,以最大迭代次数100次或优化目标(RMSE)小于0.05为终止条件,开始PSO算法的优化迭代,各粒子每更新一次位置就训练一次CNN模型,RMSE的迭代收敛过程如图6所示。特别地,运用Python的time()函数计算模型训练和预测时间,可知CNN每训练一次模型耗时约7.13 s,100次迭代完成后得出最终模型的训练耗时总计约5.94 h。在完成训练后,使用最终模型对一组数据进行预测,预测时间约为1 ms。由以上分析可知,本文建立模型所消耗的时间主要集中在训练阶段,而在预测阶段的耗时非常少,模型预测效率高。 图6 算法收敛过程 表4 优化后的卷积神经网络结构参数 3.2.3对比分析 本文基于多源异构数据和PSO-CNN在训练集数据上训练建成的表面粗度预测模型(模型M),在测试集数据上测试模型M的预测性能。模型M在训练集和测试集上Ra真实值和预测值的偏差情况如图7所示。为展现本文基于多源异构数据和PSO-CNN所建立模型M的优势,将其与以下模型进行对比分析: (a)训练集 (1)模型1为基于工艺参数、工件材料、刀具直径等静态数据和浅层神经网络的拟合模型。 (2)模型2为基于静态数据、振动信号和PSO-CNN建立的模型。 (3)模型3为基于多源异构数据和浅层神经网络建立的模型,其中,针对动态数据,人工提取均值、标准差、方差、均方根、峰峰值、偏度、峭度、波形因子等特征。 (4)模型4为基于多源异构数据和传统CNN建立的模型。 上述4个模型在测试集上的Ra预测值和真实值对比如图8所示。 图7b、图8直观展示了各模型在测试集上的预测效果,对比模型M与模型1、模型2可知,使用多源异构数据比使用较少种类数据有很大的优势。对比模型3、模型4可知,传统CNN自动提取动态数据特征优于人工提取动态数据特征。对比模型M与模型4可知,基于PSO-CNN建立的模型预测精度相比传统CNN有较大的提升。上述模型的评价指标如图9所示。 (a)模型1 已知R2值越接近1,RMSE、MAE值越小模型预测精度越高。据图9可知,模型1仅使用静态数据,在测试集上的R2值、RMSE值、MAE值分别为0.8404、0.1636、0.1333,其预测精度最低。模型2因引入了振动信号,其预测精度较模型1有所提高;模型M则基于静态数据和振动信号、力信号及功率信号等多源异构数据,全面考虑了数控铣削过程的信息,因此模型M的预测精度相比模型2有很大提升。 (a)各模型在测试集的R2对比 模型3、模型4和模型M均是基于多源异构数据建立的,其中,模型3采用人工提取特征的方式提取动、静态数据特征,损失了较多有用信息,因此在测试集上的R2值、RMSE值、MAE值分别为0.8990、0.1302、0.1090,预测精度低。基于传统CNN建立的模型4的R2值、RMSE值、MAE值分别为0.9480、0.0921、0.0812;采用PSO-CNN建立的模型M的R2值、RMSE值、MAE值分别为0.9792、0.0582、0.0476,对比模型M与模型4的评价指标可知,PSO-CNN的RMSE值、MAE值明显小于传统CNN的相应值,且R2的值更接近于1,因此PSO-CNN优于优化前的传统CNN。 通过对比可知,本文基于多源异构数据和PSO-CNN建立数控铣削表面粗糙度预测模型有较大的优势。 本文以某大型自走式采棉装备工件为例,布置振动传感器、测力仪、功率传感器以获取该工件加工过程的多源异构数据。图10a中工件材料为45钢,图10b中工件材料为6061铝合金,需要多组工艺参数、多个工步完成铣削加工,铣削工件所采集的数据见表5。 (a)45钢工件 对表5中的静态数据和传感器采集的动态数据进行处理,通过本文提出方法建立的模型预测工件在每个工步下的表面粗糙度。表面粗糙度的预测值与真实值对比如图11所示。 表5 工件铣削加工数据 由图11可以看出,各个工步工件表面粗糙度的预测值与真实值的折线基本吻合,表明本文所建立的数控铣削表面粗糙度预测模型基本可以准确预测工件加工过程中的表面粗糙度。经计算,模型在各个工步预测值与真实值的绝对百分比误差在4.18%~8.73%范围内,均小于10%;平均绝对百分比误差为6.38%,表明了本文所提的表面粗糙度建模方法的有效性。 图11 加工过程中粗糙度预测值与真实值对比图 (1)本文提出了一种基于多源异构数据的数控铣削表面粗糙度预测方法,综合考虑工艺参数、多种工件材料、多种刀具直径及多种传感器信号并采用PSO-CNN建立模型,提高了表面粗糙度预测的泛化性与精确性。 (2)对比基于本文方法建立的模型与基于较少数据种类建立的模型、基于传统CNN建立的模型的预测性能,结果表明,基于本文方法所建模型的决定系数、均方根误差、平均绝对值误差指标最优,体现了本文方法的优越性,通过某大型采棉装备的两个零件铣削加工案例验证了本文模型的有效性。 (3)本文提出的基于多源异构数据的数控铣削表面粗糙度预测方法提高了预测模型的泛化性与精度,为生产制造中制定相关优化决策提供了基础。未来的研究重点将是研究表面粗糙度与工艺参数、加工条件的关系并进行优化以提升产品质量、生产效率等。2.3 表面粗糙度预测模型训练与测试流程
2.4 表面粗糙度预测模型评价方法
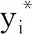

3 案例分析
3.1 实验设备及条件
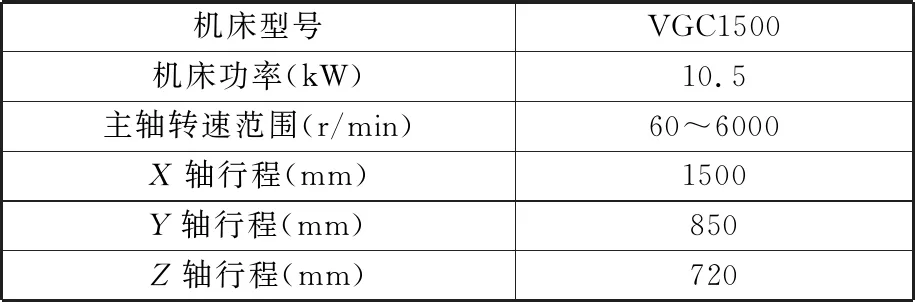

3.2 表面粗糙度预测建模与分析
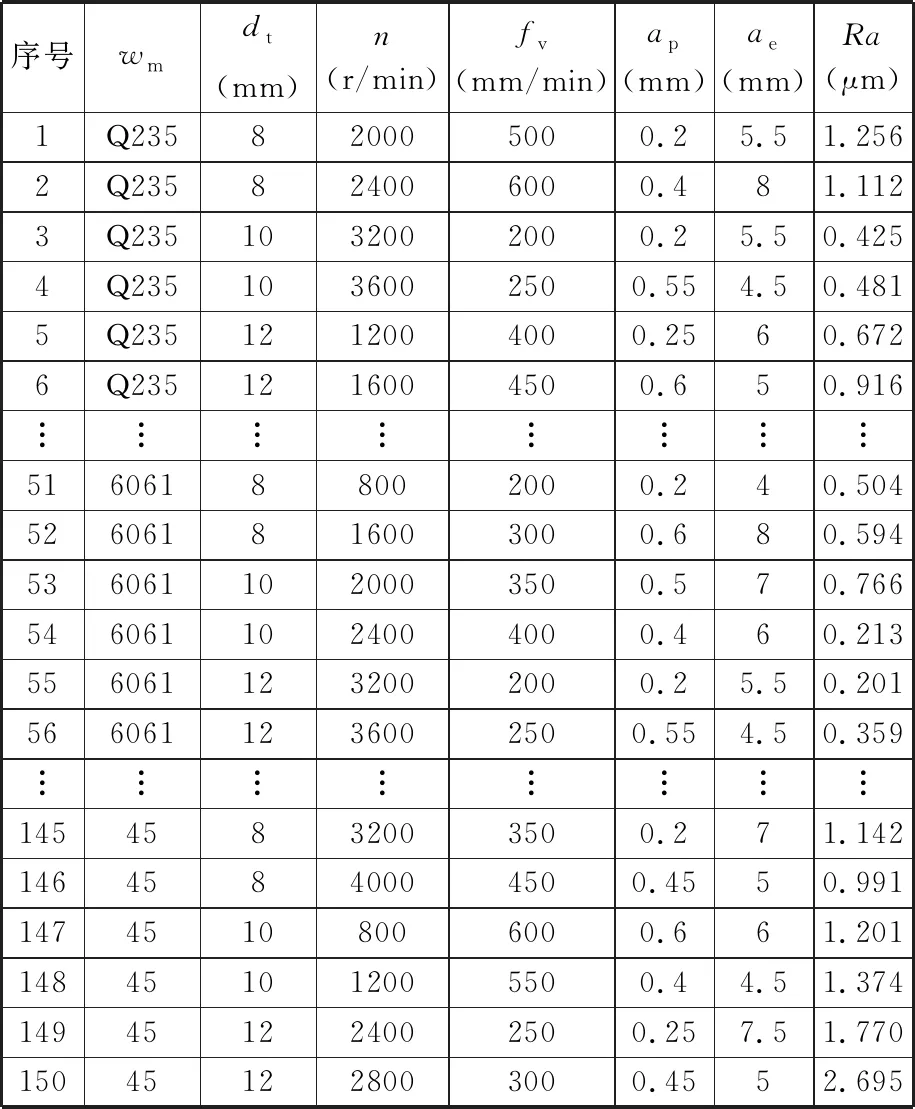
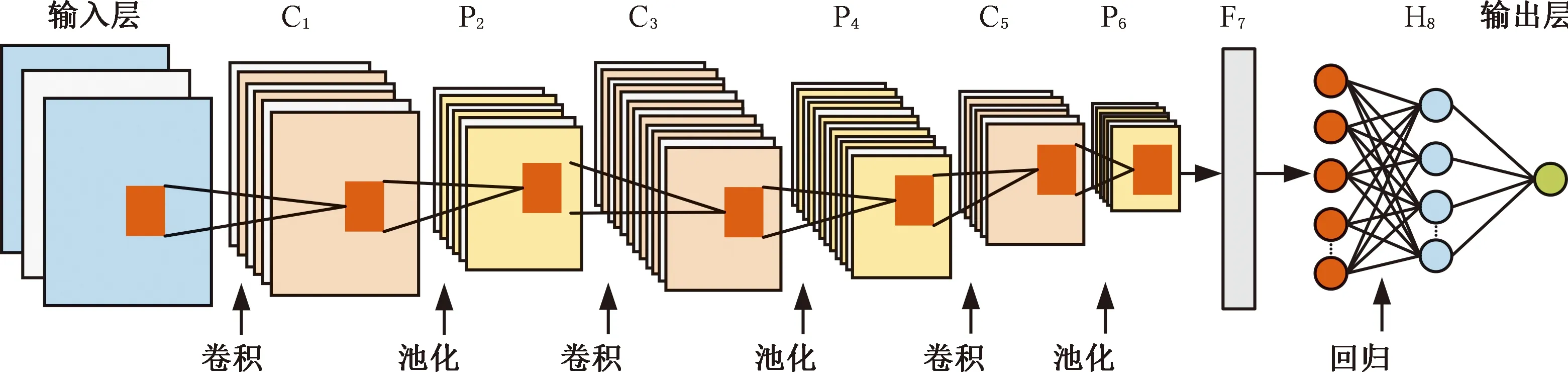

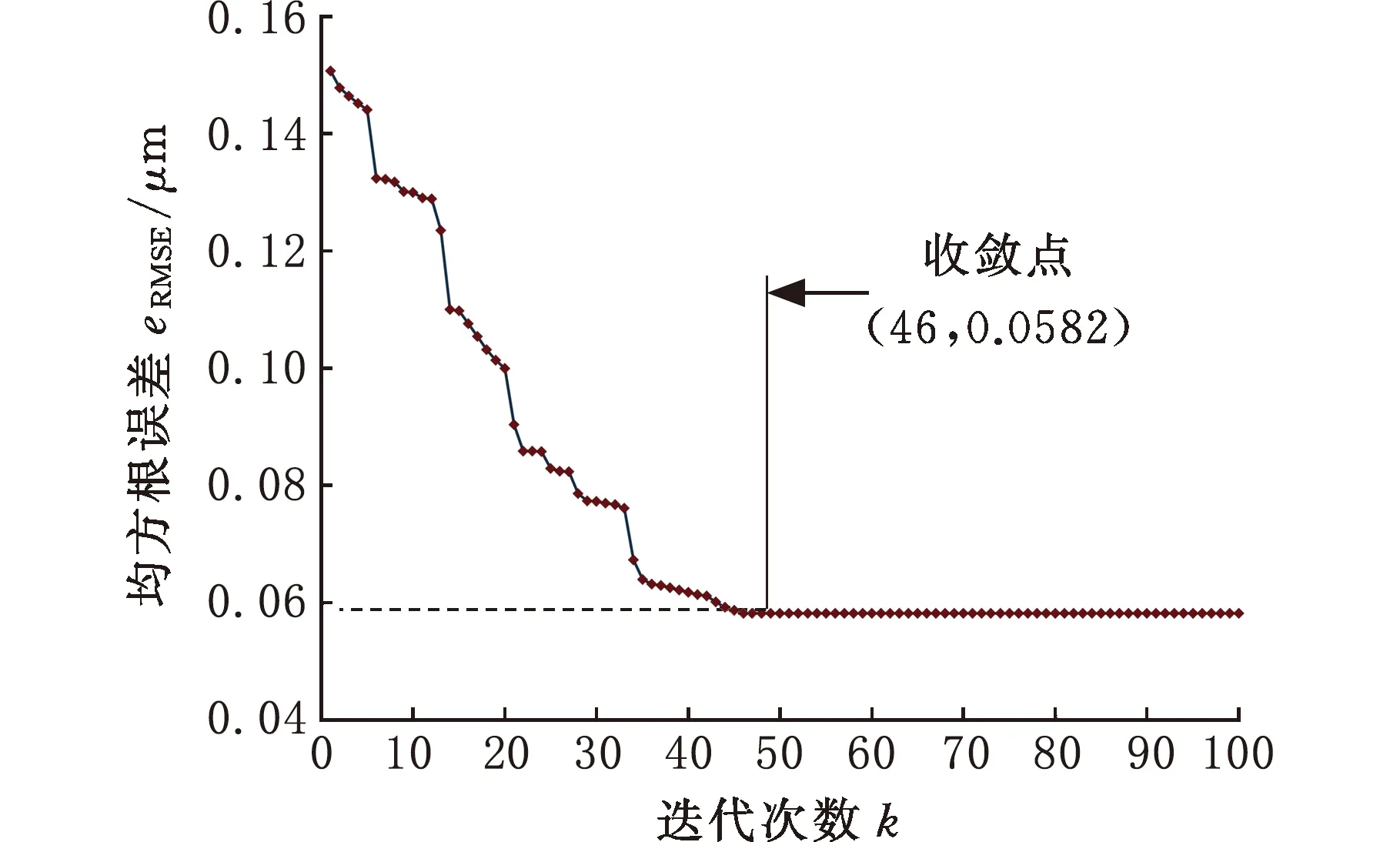





3.3 预测结果验证

4 结论

