轨道车辆三电平中点自平衡电路拓扑研究

张泽，李蔚，黄权威，张文璐，于越，刘纪龙,2

(1.中南大学 交通运输工程学院，湖南 长沙 410075；2.中车青岛四方机车车辆股份有限公司，山东 青岛 266111)

超级电容作为一种新型储能装置，与传统电容器相比，它具有较大的容量、较宽的工作温度范围和极长的使用寿命[1-2]，因此，超级电容适合作为轨道车辆的储能介质。直流变换器是轨道车辆充电系统的核心，决定充电品质的优劣。与传统的两电平直流变换器相比，三电平直流变换器的优势在于它的开关管电压应力为对应两电平结构的一半，非常适用于高电压大功率的应用场合[3-7]。现有的轨道车辆充电系统中，为了确保变换器可以得到三电平波形，一般采用2只开关管以相差180°的驱动信号交错控制[8]。但在实际应用中，由于开关器件间存在微小差异，使得均压支撑电容不能完全均压，中点电位不平衡，输出的三电平波形不对称。针对此问题，现有的解决方法是通过调整开关管的占空比来达到均压的目的[9-12]。随着SiC和GaN等高频电子器件生产工艺不断成熟，将其应用于三电平直流变换器的学术研究也随之展开。若将SiC和GaN等高频电子器件引入，可进一步提高三电平直流变换器工作效率，减小车辆动力储能充电装置的体积及重量，但是SiC和GaN等器件的高频特性也对三电平直流变换器的稳定性提出了更高的要求[13-15]。由于采集到的电压误差信号会有延迟，高频器件的引入，会使上一个周期误差不能及时地反映在下一个周期，进而造成均压支撑电容均压策略的失效。基于上述问题，本文通过分析传统三电平直流变换器中点电位不平衡的原理，提出了一种可以靠自身结构平衡中点电位，且不受调制方法和负载限制的三电平中点自平衡电路拓扑。最后通过仿真和实验验证了拓扑的中点电位电路能实现一定的自平衡特性。

1 中点自平衡拓扑及工作原理

1.1 传统三电平中点不平衡原因分析

传统的三电平直流变换拓扑结构如图1所示[4]。其中：Q1～Q4为开关管，D1～D4为对应的体二极管，CH和CL分别为高压侧和低压侧滤波电容，Cblock为隔直电容，L为滤波电感，Uin和Uout分别为输入和输出电压。当变换器正常工作时，Cblock上的电压必须控制在Uin/2以保证每只开关管电压的应力相等。

在一个开关周期内，共有4种模态。

模态Ι：Q1和Q2导通，Q3和Q4关断。AB间电压值为UAB=Uin。

模态ΙΙ：Q1和Q3导通，Q2和Q4关断。AB间电压值为UAB=Uin-UCblock。

模态ΙΙΙ：Q2和Q4导通，Q1和Q3关断。AB间电压值为UAB=UCblock。

模态ΙV：Q3和Q4导通，Q1和Q2关断。AB间电压值为UAB=0。

设占空比为D，以D＞0.5为例，传统三电平变换器工作在三电平状态，采用交错控制方式的一个工作周期模态依次为模态Ι→模态ΙΙ→模态Ι→模态ΙΙΙ。其中模态ΙΙ和模态ΙΙΙ下，Uout与中点电压相关，只有当这2个模态的UAB相等时，该拓扑才能输出对称的三电平波形。但由于Cblock在模态ΙΙ充电，在模态ΙΙΙ为放电，实际情况中Cblock容量有限，且电容充放电速度不同，在充放电时间相等的情况下，Cblock上的电压将产生小的偏移，无法维持在输入电压的一半。若不加以控制，在多个周期后，三电平甚至会退化为两电平。

1.2 中点自平衡优化拓扑工作原理

中点自平衡三电平直流变换拓扑结构如图2所示。UH为高压侧，UL为低压侧，L为滤波电感，CH和CL为滤波电容，C1和C2作为参数相同的均压支撑电容。Q1，Q2，Q3，Q4和Q5是5只开关管，D1，D2，D3，D4和D5分别是对应的体二极管，D6为续流二极管。

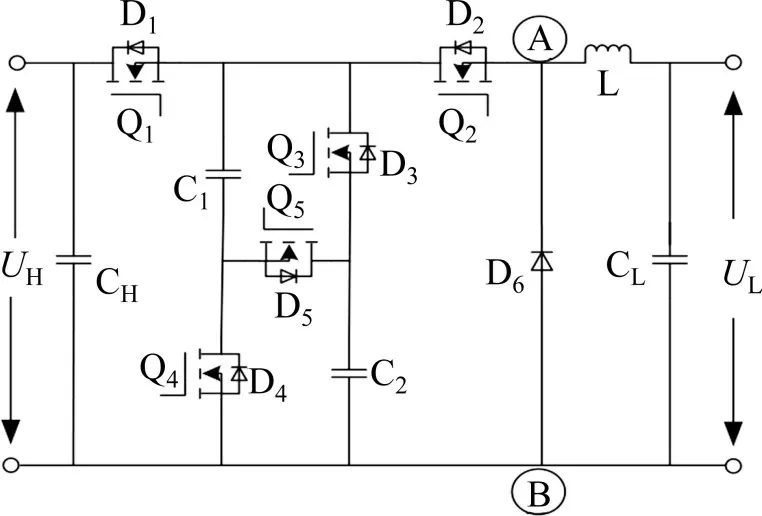
图2 中点自平衡三电平直流变换拓扑结构Fig.2 Three level neutral point self balanced DC/DC converter topology

图3 (a)中，当Q1开通时，电流从Q1流经均压支撑电容C1，体二极管D5及电容C2回到电源负极。由于UH=UC1+UC2，假设C1与C2初始电压值相同，经过充电后，UC1=UC2=UH/2。图3(b)中，当Q1关闭，Q2导通时，一方面，电流从C1流出，经Q2，负载，D4回到C1负极；另一方面，电流从C2流出，经Q3，Q2，负载回到C2负极；且2电路是并联的，假设所有元器件都是理想的，则C1与C2并联给负载放电，且放电量相同。故此拓扑结构在充电与放电过程中都能保证UC1=UC2。即使在初始时刻，出现UC1≠UC2，假设C1＞C2，由于在输入电压源给均压支撑电容充电过程中，C1与C2是串联状态，即UDC=UC1+UC2，由于C1＞C2，在放电过程中，由于C1与C2是并联状态，C1会给负载和C2放电，这样C1与C2逐渐趋于一致，最终使UC1=UC2。

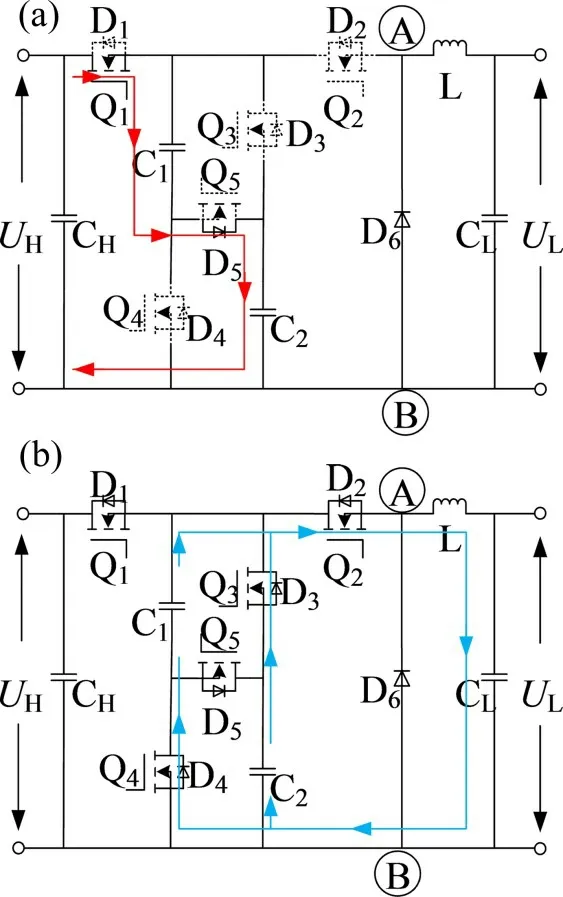
图3 中点自平衡拓扑工作原理Fig.3 Working principle of neutral point self balanced topology

2 三电平中点自平衡拓扑理论分析

在分析工作原理之前做如下假设：1)所有元器件均为理想器件。2)两端口电容CH和CL足够大，可以等效为电压源UH和UL。

稳态工作时，根据占空比的不同，变换器会有不同的工作模式。在同一种占空比的情况下，变换器仍会有Buck与Boost 2种工作模式，故变换器共有6种工作模式。如图4所示，当Q3，Q4和Q5恒关断时，变换器工作在Buck模式，共有3种模态；当Q1和Q2恒关断时，变换器工作在Boost模式，共有3种模态。本文以Buck模式为例分析其模态如下。

图4 中点自平衡三电平优化拓扑Buck模式等效电路Fig.4 Buck mode equivalent circuit of neutral point self balanced three level topology optimization

模态Ι：Q1和Q2导通；此时，一方面，输入电流流经C1，D5，C2，给C1和C2充电，另一方面，流经Q1，Q2，L，给负载充电，电感电流从A流向CL，将该方向定义为正向电感电流方向。输出电压UCL=UH，电感电流线性增加；如图4(a)所示。

模态ΙΙ：Q2导通，Q1关断；此时，C1和C2并联给负载放电，输出电压UCL=UH/2；如图4(b)所示。

模态ΙΙΙ：Q1导通，Q2关断；此时，C1和C2串联充电，电感L通过二极管D6续流；如图4(c)所示。

Buck模式下，能量从H端口流向L端口，输出电压为DUH，各开关管承受的压力为UH/2。稳态时，由于电容C1和C2一直处于“串联充电，并联放电”的状态，故UC1=UC2=UH/2。UL和UH的关系如下：

3 参数计算

上文通过理论分析证明在理想情况下，本文所提出的拓扑具有中点自平衡能力，但在实际情况中，拓扑的自平衡能力还与元器件的参数息息相关。下面以Buck模式为例，说明本拓扑在实际情况下主要元器件参数选取原则。

3.1 电感计算

本文立足于轨道车辆超级电容充电装置对纹波有较高要求的前提下，考虑用Buck电路的CCM模式作为滤波电感的计算原则。

3.1.1 CCM模式(连续导通模式)

当变换器工作在CCM模式时，其波形如图5所示。

阶段2[t2,t4]：功率器件Q2导通，Q1关断，电容C1和C2通过电感L并联给负载供能，电容电压UC1和UC2同步下降；在此阶段中UAB=UH/2，UH/2-UCL施加在电感L上，因此电感电流iL线性增加。

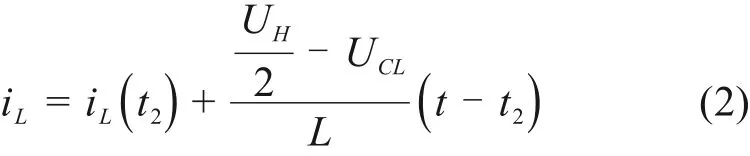
Buck模式(UCL＜0.5UH)下，UH与UCL之间的关系是：

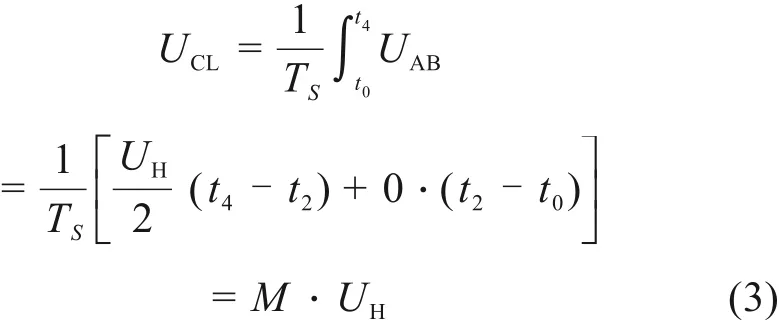
式中：M为电压增益。

图5 (b)显示了CCM模式下Buck变换器在UCL＞0.5UH情况下的主要波形。利用相同的分析方法可得Buck模式(UCL＞0.5UH)中，UH与UCL之间的关系是：

3.1.2 DCM模式(不连续导通模式)

随着电感值L减少，图5的电感电流波形将整体下移，当电感电流的波谷值iLmin＜0时，Buck三电平变换器则工作在DCM模式，如图6所示。

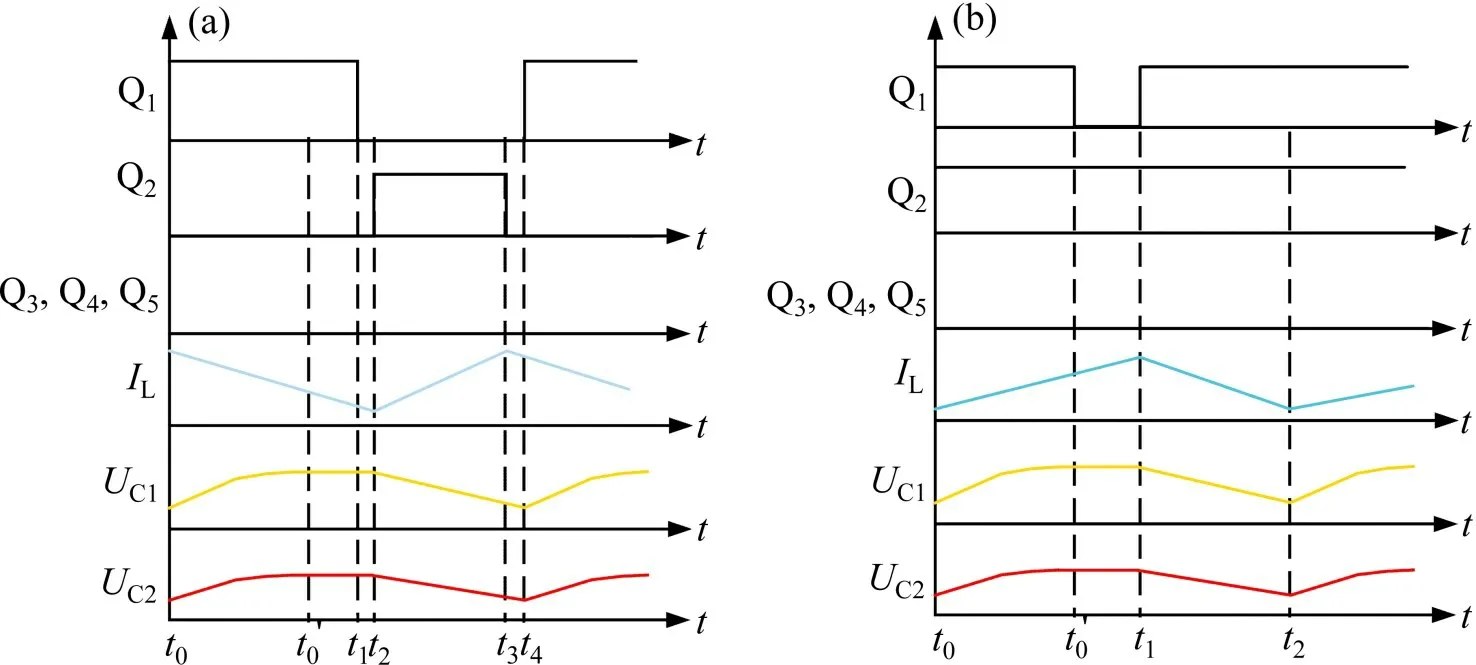
图5 CCM模式下Buck变换器的波形示意图Fig.5 Waveform diagram of Buck converter in CCM mode

以UCL＜0.5UH为例，在一个开关周期内，变换器仍可分为2个阶段。[t0,t2]，[t2,t4]工作状态与CCM时类似；在t0～t0`内，电感电流线性减少，且于t0`时刻降至0，此时电容电压UC1和UC2充能；在t2～t3内，电容C1和C2为负载提供能量，电感电流线性增加。

3.1.3 DCM与CCM间的临界电感

由上文分析可知，DCM与CCM的临界条件为：iLmin=0。

当UCL＜0.5UH时：临界条件下电感电流平均值可以表示为：

临界条件下电感电流峰值为：

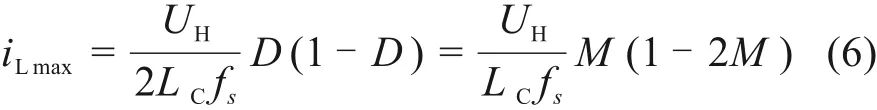
式中：LC为临界电感值，fs为功率器件的开关频率，M为电压增益。故在UCL＜0.5UH时，CCM与DCM间的临界电感值为：

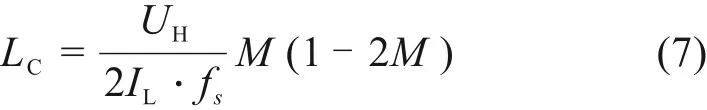
当UCL＞0.5UH时：临界条件下电感电流平均值可以表示为：

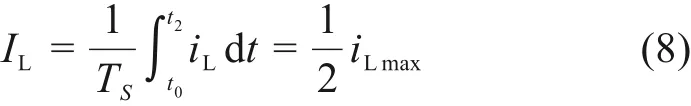
临界条件下电感电流峰值为：

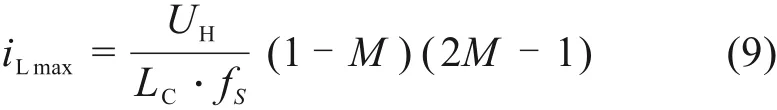
故在UCL＜0.5UH条件下CCM与DCM间的临界电感值为：

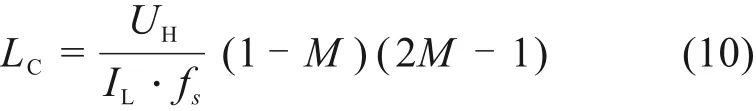
CCM与DCM间的临界电感值关于电压增益M和电感电流平均值的函数曲面如图7所示。

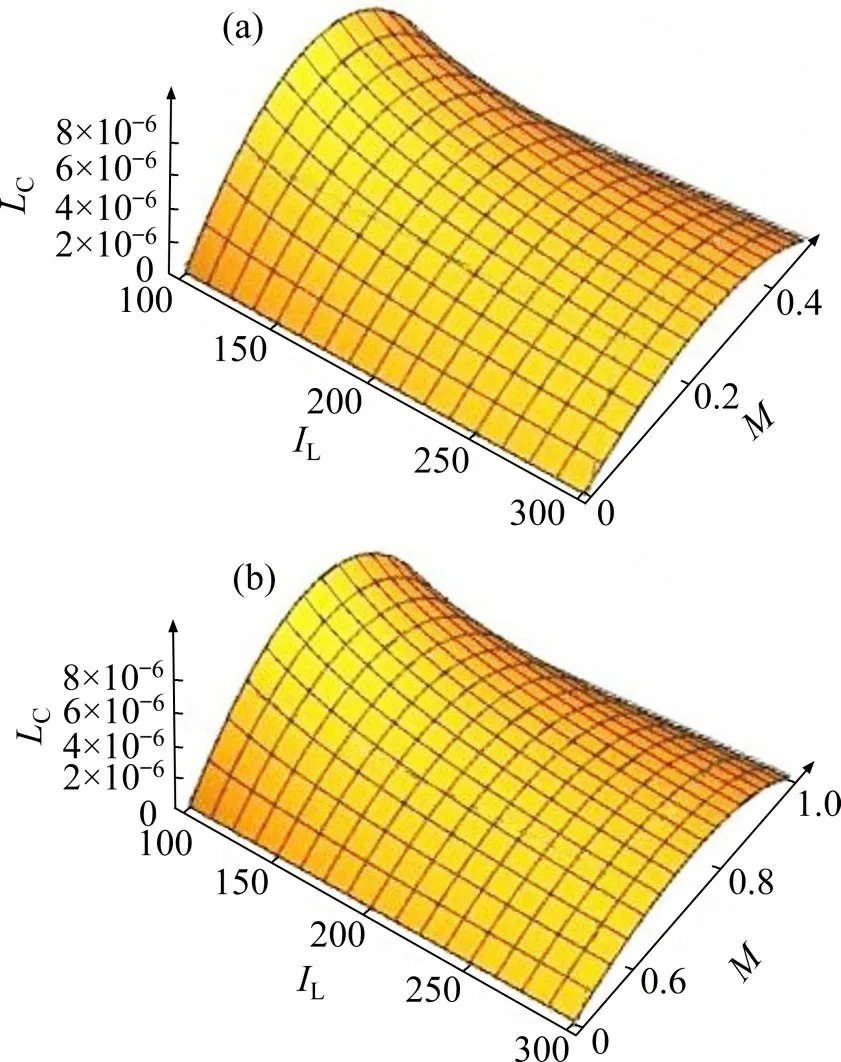
图7 CCM与DCM间的临界电感值关于电感电流和M的函数曲面Fig.7 Function surface of critical inductance between CCM and DCM with respect to sum M

由图7可知，临界电感与电感电流成反比。在增益为0.25或0.75时，临界电感值最大。设最大增益为Mmax，应按照以下原则选取电感：

当Mmax＜0.25时，以最大增益时的临界电感为标准。

当0.25＜Mmax＜0.75时，比较最大增益时的临界电感与增益为0.25时的临界电感大小，以较大电感值为标准。

当Mmax＞0.75时，比较增益为0.25和增益为0.7时的临界电感大小，以较大电感值为标准。

3.2 均压支撑电容计算

实际中，均压支撑电容C1和C2充电与放电的速度是不相同的，放电速度要远远高于充电速度，且与负载初始电压值有关。

设U0为电容上的初始电压值；U1为电容最终可充到或放到的电压值，Ut为t时刻电容上的电压值，则：

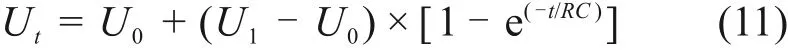
以UCL＜0.5UH情况为例，系统分析均压支撑电容在充电和放电过程中的数学模型如下所示：

充电过程：

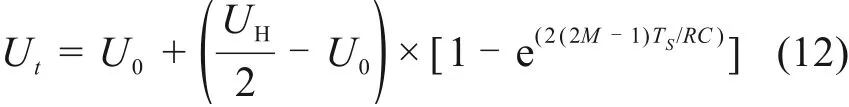
放电过程(假设为恒流放电)：

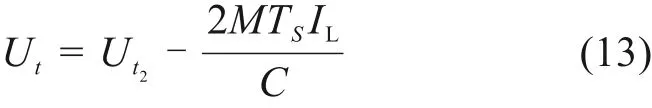
CCM模式(UCL＜0.5UH)中，一个开关周期内，均压支撑电容电压变化为：

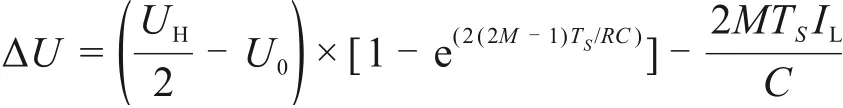
式中：M为电压增益，C为单个均压支撑电容容值，IL为电感电流平均值，(UH/2-U0)仅与均压支撑电容的电压允许波动量有关，故可以设为δ。对于均压支撑电容变化量有如下表达：

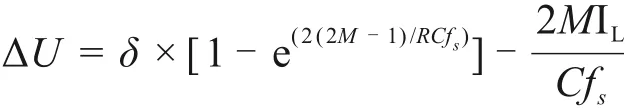
令ΔU=0，可知CCM模式下在电感电流与电压允许波动量一定时，电压增益与电容容值以及开关频率的关系如图8所示。在保证中点电位平衡的前提下，电压增益随着电容容值增加而增加，当容值达到一定值时，电压增益将不再随电容容值改变。开关频率与电压增益变化规律类似，因此可依据此关系曲线，选取最优电容容值及开关频率。CCM模式下在电压允许波动量与开关频率一定时，电压增益与电容容值以及电感电流的关系如图9所示，在放电电流较小情况下，可保证较大的电压增益，但随着放电电流增大，电压增益急剧下降。以上分析可知，支撑电容不能选择太小，否则电压允许波动值太小，均压支撑分压电容放电速度大于充电速度，中点电位向下偏移。均压支撑电容也不宜选太大，因为当均压支撑电容到一定值后，再增加其容值时，对提高中点稳定性的意义不大。

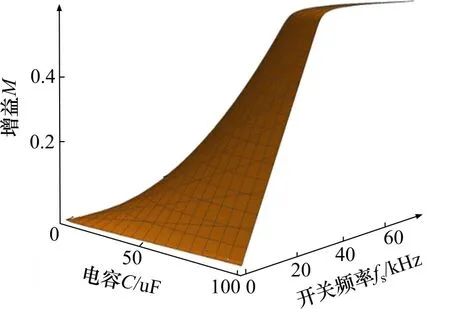
图8 电压增益关于电容容值和开关频率之间关系的函数曲面Fig.8 Function surface of voltage gain with respect to the relationship between capacitance and switching frequency

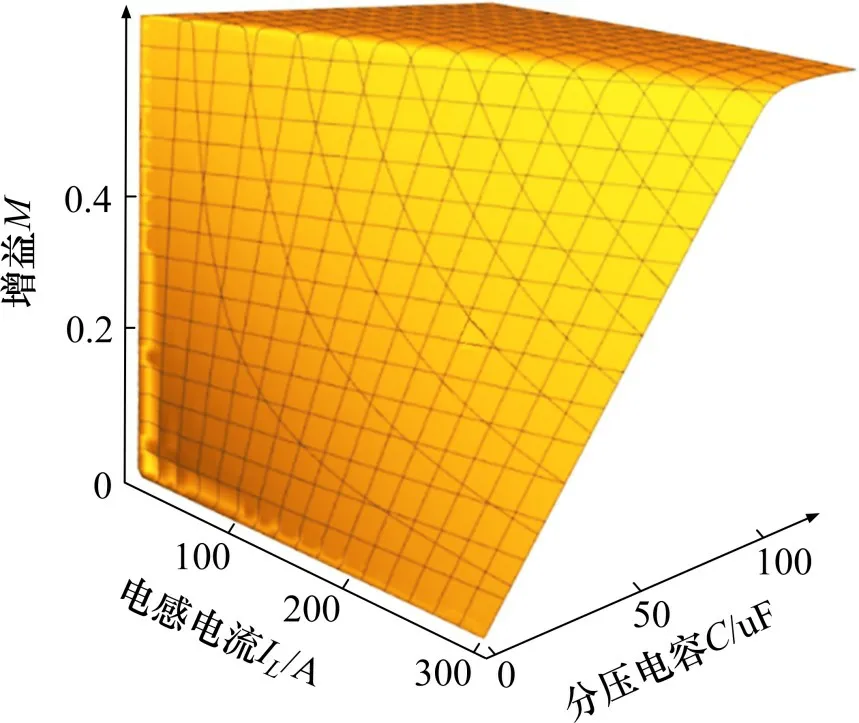
图9 电压增益与电容容值以及电感电流之间关系的函数曲面Fig.9 Function surface of the relationship between voltage gain and capacitance value and inductance current

4 仿真及实验证明

为了进一步验证本文所提供方案的可行性，本文进行了仿真分析及实验验证。

4.1 仿真分析

本节利用Matlab/Simulink对电路进行仿真分析。仿真所用参数分别为：电源DC1 500 V，均压支撑电容容值设为930 uF，滤波电感值设为51 uH，超级电容容值设为0.6 F，开关管开关频率为50 kHz。

图10 为三电平自平衡优化拓扑采用恒压恒流控制策略进行仿真所得的中点电位波形图。由仿真波形图可以得出以下结论：Q1导通，Q2关断时，电容C1和C2电压同步提升，表明C1和C2串联充电，UC1=UC2，中点电位升高；与理论分析一致。Q1关断，Q2开通时同样与理论分析一致。

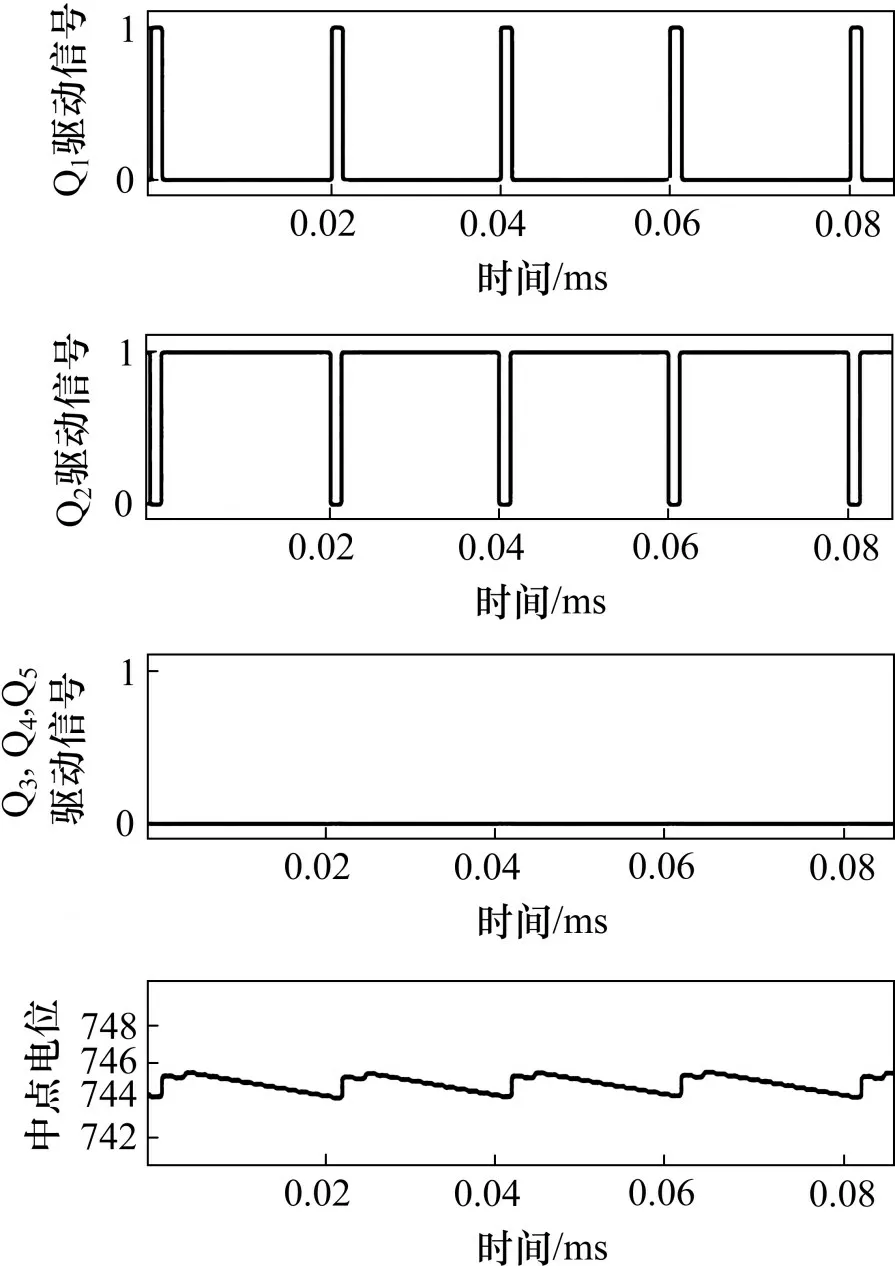
图10 驱动信号及中点电位波形图Fig.10 Waveform of driving signal and neutral point potential

图11 三电平自平衡优化拓扑实验平台Fig.11 Three level self balancing topology optimization experimental platform

4.2 实验验证

实验所用元器件参数分别为：DC1500V电源，型号为B25620B1427A101的均压支撑电压、电感值为51 uH滤波电感，型号为CAS300M17BM2的SiC MOSFET管。实验通过示波器采集中点电位波形如图12～13所示。

实验结果分析：传统三电平拓扑未加中点电位控制策略时，均压支撑电容会从预充电后的750 V降至600 V左右，如图12所示。本文所提出的中点自平衡拓扑在同等条件下，均压支撑电容稳定在750 V左右，放大10倍后可看出电容电压上下波动3 V左右，如图13所示。实验结果证明本文所提出的拓扑在不加中点电位控制策略情况下，依旧可以维持均压支撑电容电压为输入电压的一半。

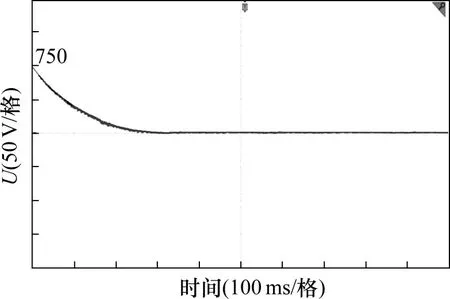
图12 传统拓扑均压支撑电容电压波形图Fig.12 Voltage waveform of voltage divider capacitor in traditional topology

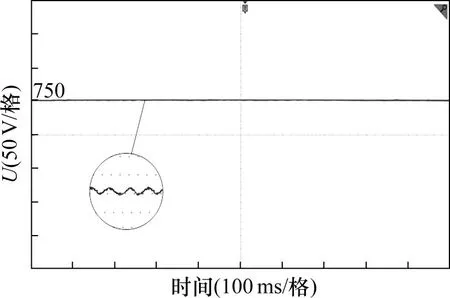
图13 优化拓扑均压支撑电容电压波形图Fig.13 Voltage waveform of voltage divider capacitor with optimized topology

5 结论

1)相较于现有的轨道车辆充电系统中三电平直流变换拓扑，本拓扑能实现一定的中点电位自平衡，且不依赖于控制算法，可以极大地简化系统的算法复杂程度，有效提高系统的稳定性。

2)相较于现有的轨道车辆充电系统中三电平直流变换拓扑只有一个均压支撑电容充放电的特点，本拓扑“串联充电，并联放电”特点，即在U/2模态下两电容并联给超级电容放电可以更好地维持中点电位的稳定性。

3)提出一种均压支撑电容的选型原则，可以有效降低均压支撑电容的纹波。