基于PCA-PSO-SVM的球磨机负荷预测研究
冯先丁,魏镜弢,吴张永,钱 杰,浦友尚
(昆明理工大学 机电工程学院,云南 昆明 650500)
磨矿作业是选矿流程中非常关键的环节[1],其负责最大限度地解离矿石中的有用矿物和脉石矿物。磨矿产品的质量直接影响整个选矿厂的技术指标和经济效益。磨矿作业是选矿厂中能源消耗最大的环节,其生产成本占整个选矿厂生产总成本的45%~60%,因此准确有效地预测球磨机内部的运行状态及优化磨矿控制技术是选矿行业提高选矿效率、提升企业效益的关键环节[2]。
早期的工人根据球磨机的声音和个人经验[3]来判断球磨机内部的负荷状态。由于球磨机工作时影响因素众多,内部环境复杂,故这些方法误差较大。文献[4~6]中,研究人员通过采集球磨机外部信号来预测球磨机负荷。近年来,磨音信号成为了研究的热点。文献[7]通过采集球磨机磨音信号,对起磨过程磨音和停磨过程磨音进行了功率谱估计,得到磨音的有效频段。然后将有效频段分段后的能量作为特征,采用径向基(Radial Basis Function,RBF)神经网络建立预测模型来预测球磨机的负荷。文献[8]采用主元分析法(Principal Component Analysis,PCA)对振动谱能量值进行降维,利用支持向量机(Support Vector Machine,SVM)建立磨机负荷参数分类模型,实现了磨机负荷的预测。该研究证明,球磨机磨音信号与球磨机负荷有紧密的联系。上述方法在对球磨机信号进行频谱特征提取时,由于受到人为分析不精确和考虑不足等因素的影响,导致产生频段被硬性划分或无法准确找到反映球磨机负荷特征等问题。此外,上述方法在建立预测模型时没有考虑 SVM 的最佳参数,导致球磨机预测精度低,模型性能不稳定。因此,本文提出一种基于PCA-PSO-SVM的球磨机负荷预测模型。
1 磨音信号与负荷的联系
球磨机产生的声音主要包括磨音和各种干扰噪音[9]。磨音主要分为两部分:(1)由磨矿介质与球磨机内衬板碰撞产生的声音。这部分声音主要受到球磨机的转速和磨矿介质的填充量的影响。一般在工程中使用的球磨机转速较小,所以这部分磨音主要集中在中低频[10];(2)由筒体内磨矿介质与磨矿介质、磨矿介质与物料之间相互撞击产生磨音。由于磨矿介质数量多、体积小,碰撞机会大,所以产生的声音以中高频为主。
在磨音中,磨矿介质和磨矿介质之间、磨矿介质和物料之间撞击产生的声音主要受筒体内的负荷影响。当负荷较小时,所发出的磨音主要是磨矿介质之间的冲击和碰撞声。此时磨音的频率高,声响大,听起来比较清脆。当球磨机内的负荷较大时,由于筒体内磨矿介质之间的空隙逐渐被物料填充,磨矿介质以及物料间的碰撞和冲击次数减少,此时的磨音频率低,声响小,听起来比较低沉。本文根据磨音信号与负荷之间的联系,通过对磨音信号进行采集、处理和分析,可有效预测球磨机负荷对。
2 信号特征提取与PSO-SVM参数优化
2.1 Welch法功率谱估计
Welch算法是对周期图法的改进算法[11]。将样本数据进行分段加窗处理,求得各段功率谱后再求平均功率谱[12]。将信号x(n)的N个数据点分为L段,每段长度为M。
如果对每一段的数据点加矩形窗,第i段的数据变成
(1)
由此可以得到平均周期图法
(2)
这种方法也称为Bartlett法。
采用Welch法对信号数据点分段时,对每段数据之间做一个交叠,并且在对数据段加窗时可以选择多种窗。按Bartlett法对数据段求取功率谱,对所求的结果进行归一化处理,得到
(3)
式中,U为归一化因子;d2(n)为数据加窗函数。
相比于周期法,Welch法可有效改善谱曲线的光滑性,并提高谱估计的分辨能力[13]。
2.2 主元分析法
主元分析法是特征提取和数据压缩中的经典方法[14-15]。PCA用较少的主元变量反映大部分原始数据的信息,可以有效降低特征维数。PCA的实现算法步骤如下[16]:
步骤1数据标准化处理。对原始数据进行z-score标准化处理,使得不同指标具有相同的数量级和量纲,便于后续计算和分析。标准化计算式为
(4)
式中,yij为矩阵中的第i个样本的第j个观测值;yj为矩阵Y中第j列均值;sj为第j列的标准差;
步骤2计算样本矩阵的相关系数矩阵R。相关系数矩阵计算为
(5)
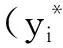
(6)
式中,m为样本总数据;
步骤3求协方差矩阵的特征根和特征向量。根据特征方程|λE-R|=0可求出特征根,并按照大小顺寻排列为λ1≥λ2≥…≥λn≥0。与特征根相对应的特征向量为α1,α2,…,αn。特征向量组成的矩阵特为特征向量矩阵,如式(7)所示。
(7)
式中,n为样本数据的观测量;
步骤4计算主元矩阵T。主元ti=Yαi表示了原始信息矩阵在某个主元下对应向量上的投影,它的大小表示了Y在αi方向上的覆盖程度。主元矩阵T为
T=Ym×nLm×n=t1,t2,…,tn
(8)
式中,Ym×n为样本原始数据矩阵;
步骤5计算主元贡献率和累计贡献率。主元贡献率为主元所携带的信息占所有信息的百分比。每个成分变量所携带信息可以由其方差来表示,所以每个主元的方差占总方差S的百分比就是该成分的贡献率,如式(9)所示。
(9)
前r个主元累计贡献率也就是前r个特征值的累计方差值贡献率,如式(10)所示。
(10)
依据累计贡献率来选取主元,当累计贡献率达到 90%或者以上时,前r个主元就能反映出原有数据信息样本变量包含的大部分信息,即用较少相关的特征代替了原有的特征。
2.3 粒子群优化算法
粒子群优化(Particle Swarm Optimization, PSO)算法通过追随当前最优值来寻找全局最优。PSO 算法具有并行性、分布式处理的特点,得到了广泛的研究和应用[17-18]。
PSO算法中粒子群迭代更新的过程为:假设在一个D维空间中,一共有N个粒子,第i个粒子在D维空间中的飞行速度向量为
vi=(vi1,vi2,vi3,…,viD)
(11)
位置向量为
xi=(xi1,xi2,xi3,…,xiD)
(12)
每次迭代,粒子根据适应度函数算出相对应的适应值,依据自己和群体的经验来更新下一次迭代的位置和速度,将表述转化为直观的计算式
(13)
(14)
式中,k为迭代次数;xik为第i个粒子在第k次迭代中的位置向量;vik为第i个粒子在第k次迭代中的速度向量;pi是第i个粒子个体经历过的最好位置;gi是迭代到目前种群所经历过的最好位置;r1和r2为随机函数;c1和c2为认知因子和社会学习因子;ω为惯性权重。
2.4 支持向量机
支持向量机是建立在结构风险最小原则和统计学理论基础上的一种机器学习方法。SVM最早被用于解决分类问题,后又将其应用于解决回归分析和函数拟合问题[19]。最优分类函数表示为
(15)
式中,λi为拉格朗日乘子;b为偏置;xi为数据点;yi为类别。
将上式用于处理非线性样本时,其无法准确划分样本,因此引入了惩罚函数C、不敏感损失参数ε和核参数g。惩罚因子主要表示模型对误差的容忍度。不敏感损失参数主要影响学习机的拟合效果,其取值越小,模型的复杂程度越大,拟合的精度也就越高。核函数决定了数据从原始空间映射到更高维的特征空间的分布情况,从而影响模型的泛化性能。
3 建立负荷预测模型
3.1 数据准备和预处理
搭建球磨机磨音采集系统,采集10个负荷下球磨机的磨音信号,每组实验得到40个样本,共400个样本。采用PCA进行特征提取,得到每个样本的21维特征,进而得到400×21的样本集。将样本集随机分为训练集(样本个数为300)和测试集(样本个数为100)。为了便于分析并提高计算效率,在进行模型建立之前需对样本数据进行归一化处理,将原始数据规范到[-1,1]之间,表达式为
(16)
式中,x为需要被归一化的数据;y为归一化后的结果。部分数据如表1所示。
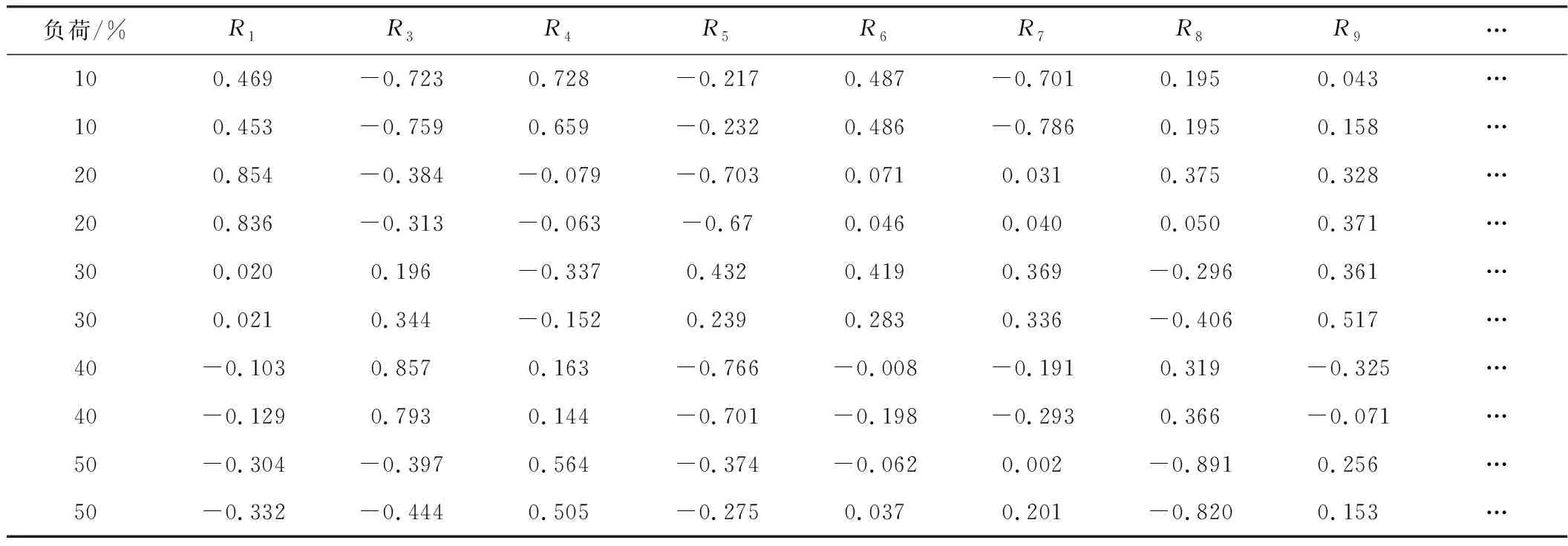
表1 归一化后的样本集(部分)
3.2 SVM参数优化
对 SVM 中的参数进行初始化设置:惩罚因子C的取值范围为(0.1,1 000),核参数g的取值范围为(0.01,100),不敏感损失系数ε的取值范围为(0,1)。PSO 中的参数设定为:种群粒子个数为 20,惯性权重w=1,学习因子c1=1.5,c2=1.7。将交叉验证法(K-CV)的均方误差平均值(Mean Square Error,MSE)作为适应度函数,以最大迭代次数 200 作为终止条件,得到支持向量机的3个参数最优取值。
3.3 建立预测模型
本文提出的基于PCA-PSO-SVM的球磨机负荷预测模型整体步骤如下:
步骤1利用实验室搭建的磨音信号采集系统采集球磨机正常工作时不同负荷下的磨音信号,并对时域信号进行样本分段;
步骤2利用Welch法计算磨音信号的功率谱,进行频谱分析,并进行分段,得到基本特征;
步骤3利用PCA主元分析法对基本特征进行特征提取,降低特征的维度和特征之间的冗余度;
步骤4利用PSO算法对SVM的3个参数进行寻优,得到最优参数;
步骤5利用寻优后得到的参数建立SVM预测模型,用训练集数据训练模型,最终对测试集进行球磨机负荷预测。
4 实验结果分析
4.1 PCA特征提取
采用主元分析法对球磨机磨音信号功率谱进行特征提取,将特征值从大到小进行排列,计算每个特征值对应的主元贡献率和累计贡献率。主元累计贡献率的变化如图1所示。
为了确保特征提取后的特征能够反映原始数据的绝大部分信息,本文将累计贡献率96%作为确定主元个数的指标,因此本文将主元个数确定为 21。
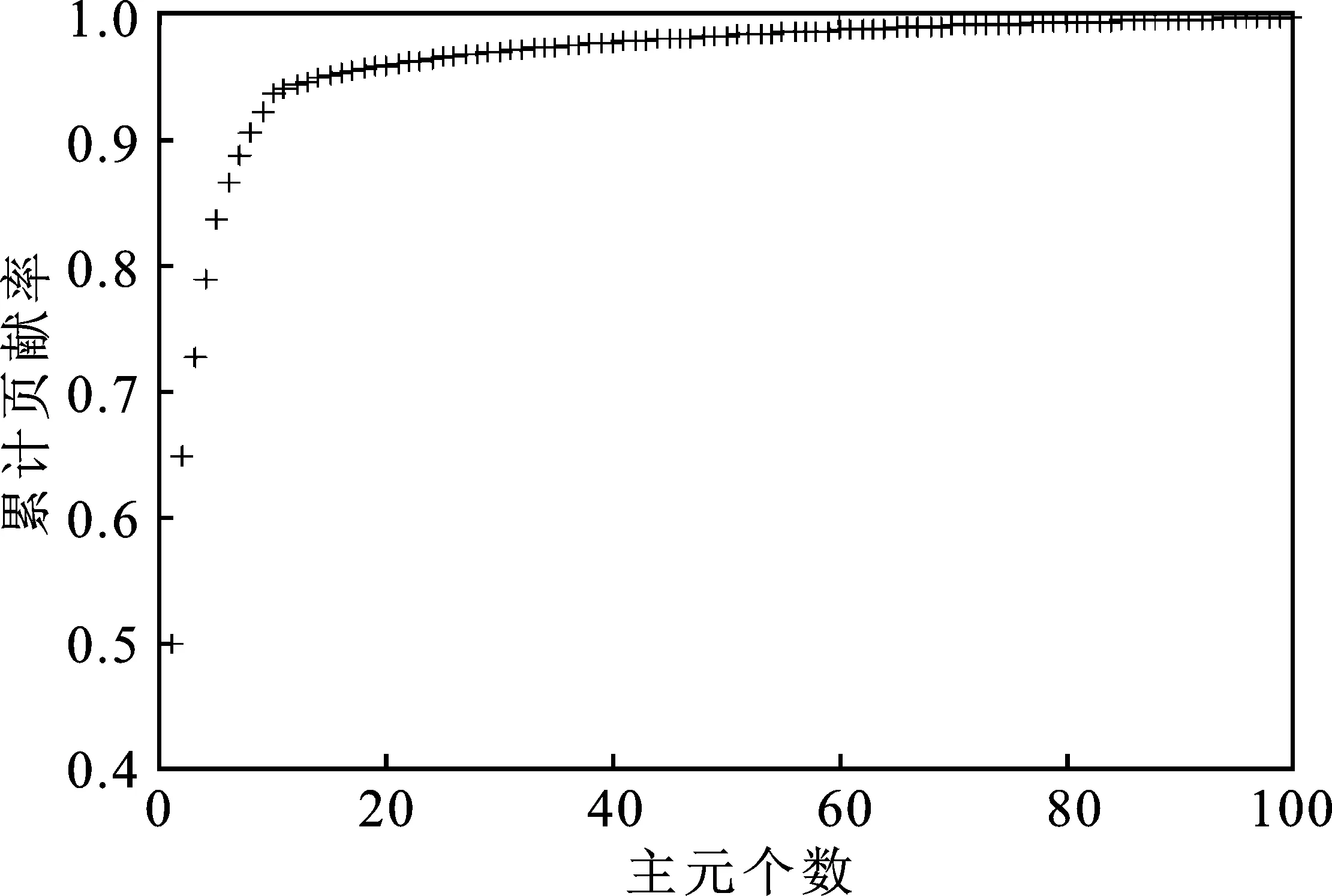
图1 主元累计贡献率变化图 Figure 1. Diagram of principal cumulative contribution rate change
4.2 参数优化结果分析
通过 150次进化迭代计算,得到支持向量机的最优惩罚因子C=89.751 2,核参数g=0.109 9,不敏感损失系数ε=0.422 35。得到的最佳适应度变化进行曲线如图2所示。

图2 最佳适应度进化曲线Figure 2. Evolution curve of best fitness
由图可知,适应度随进化代数的增加而呈阶梯式下降,说明寻优算法没有陷入局部最优值。当迭代次数到 22 次时适应度不再改变,得到最优参数值。
4.3 仿真结果对比分析
本文利用优化后的参数建立PCA-PSO-SVM预测模型。用训练集数据对模型进行训练,之后分别对训练集和测试集进行预测,得到预测结果。测试集预测结果误差如图3所示。

图3 PCA-PSO-SVM 测试集预测结果误差图
为了更好地证明本文提出PCA-PSO-SVM预测模型的精确性和稳定性,将这个模型的预测结果分别与 SVM 和 PCA-SVM预测结果进行对比分析。图4、图5分别为SVM 和 PCA-SVM的预测误差图。
为了更好地说明新预测模型的精确性和稳定性,本文引入3个评价指标:均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)以及平均百分比误差(Mean Average Percentage Error,MAPE)。对比结果如表2所示。
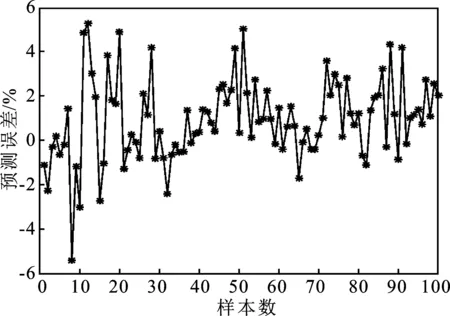
图4 SVM测试集预测结果误差图Figure 4. Error graph of SVM test set prediction result

图5 PCA-SVM测试集预测结果误差图Figure 5. Error graph of PCA-SVM test set prediction result

表2 3种预测结果评价指标
由表中信息可知,PCA-PSO-SVM负荷预测模型的各项指标都优于PCA-SVM和SVM,且PCA-SVM模型的评级指标也高于SVM。PCA-PSO-SVM负荷预测模型不仅降低了预测的误差,也提高了预测速度。
5 结束语
本文通过对样本原始数据进行Welch法功率谱分析,并利用PCA对数据进行特征提取和降维处理,不仅降低了特征之间的冗余度和特征维度,还减少了样本的干扰信息,简化了样本数据。本文通过PSO对SVM的相关参数进行寻优,得到建立该模型所需的最优参数,提高了预测模型的推广能力,提升了预测模型的预测精度和稳定性,降低了预测误差。本文提出的PCA-PSO-SVM负荷预测模型通过球磨机磨音信号准确地预测其内部负载,误差范围小,算法运算时间较短,计算效率有所提高。
由于本文的研究对象是实验室小型球磨机,故实验采用间断式给料磨矿,这与实际现场连续给料的球磨机采集的信号数据仍有差异。在今后的实际应用中,需要考虑到这一点。

