基于Simulink的批次磨矿产物粒度组成预测研究
帅智超,许文哲,朱朋岩,杨金林,马少健
(广西大学资源环境与材料学院, 广西南宁530004)
0 引言
随着矿产资源不断的开发利用,高品位矿产资源已接近枯竭,“贫、细、杂”矿石成为矿物加工的主体,其开发利用难度大,选别流程复杂,生产成本高[1]。在选矿过程中,磨矿是使矿石粒度不断减小的过程,磨矿产品粒度分布会显著影响后续选别作业的技术经济指标[2],因此,对磨矿作业中产品粒度分布的调控等进行研究很有必要。矿物资源的贫化导致选矿生产原矿性质复杂多变,磨矿过程存在多种因素不可测和过程不可控等问题,且具有非线性、大滞后和强耦合等特性[3]。磨矿数学模型主要用来描述物料破碎行为和粒度变化特征,通过数学建模对磨矿过程进行模拟和仿真预测研究,可模拟分析磨矿过程中各个粒级的磨矿行为,对实际磨矿情况作出理论上的分析和判断,同时也可以大大减少磨矿试验所消耗的时间、人力物力成本等,更科学、合理地提出磨矿优化方案,是磨矿作业调节和优化的重要途径[4]。本文以磁铁矿为研究对象,利用MATLAB/Simulink,构建以总体平衡动力学模型为基础的批次磨矿仿真预测模型,并对模型中的破裂函数和选择函数进行计算求解,并输入模型进行仿真运算,以获取磨矿产品粒度分布;同时与批次磨矿试验结果进行比较,以考察预测结果的适应性和准确性。
1 磨矿试验
1.1 试验原料、设备及试验方法
试验原料来自某矿山的磁铁矿,将原矿样品进行破碎并筛分为6个粒级,结果见表1。每个粒级分别混匀、缩分,并按其质量占比配矿。磨矿试验设备为实验室Φ200×240棒磨机,钢球介质直径为25 mm。磨矿试验条件为:磨机转速率80%,介质充填率40%,磨矿浓度70%,磨矿时间分别为1、2、3、4、6、8 min。在上述磨矿试验条件下进行批次磨矿试验,分析研究不同磨矿时间条件下的磨矿产物粒度分布。

表1 磨矿样品的初始粒度分布
1.2 试验原理
磨矿数学模型主要包括矩阵模型、n阶磨矿动力学模型、总体平衡动力学模型和智能算法模型等[5]。其中总体平衡动力学模型是基于磨矿过程中颗粒数量变化的总体平衡而建立的动力学模型,是目前磨矿解析最理想、用途更广泛的磨矿动力学框架模型[6],就批次磨矿过程而言,其基本形式为
(1)
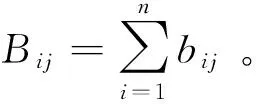
总体平衡动力学模型是基于磨矿总体物料平衡且将矩阵模型和动力学模型相结合建立的动力学模型,用矩阵表示为
(2)
(3)
上式求解的关键是获得破裂函数矩阵b和选择函数矩阵S的值,经过许多学者研究推导提出的求法主要有两种:一种为Reid[7-8]提出的解析解;另一种为数值解法,包括零阶产出率法[9]、奥-勒法[10-12]、理想混合器法[5]、G-H算法[13]、经验公式法[14-16]等。本文采用由学者Austin和Luckie提出的BII算法来计算有关参数。
BII算法由Austin和Luckie提出[11],是根据一阶动力学方程求不同粒级的选择函数S,根据求出的S值反算破裂函数B值。BII算法实际上是零阶产出率法的修正形式,其与零阶产出率法的假设相同,即累积破裂函数与选择函数的乘积为定值。
由一阶动力学方程得
(4)
式中Pi(t)为t时刻磨矿产品中粒级i的筛下累积产率。假定磨矿时间较短,无重复破碎,产物中第一粒级由给料中第一粒级破裂而来的部分为
1-Pi(t)=[1-Pi(0)]exp(-S1Bi1t)。
(5)
产物中第二粒级由给料中第二粒级破裂而来的部分为
1-P2(t)=[1-P2(0)]exp(-S1t),
(6)
可得
(7)
由式(4)得
(8)
将式(7)代入式(8)得
(9)
对于规范化的破裂分布函数,求出Bi1后即可得出
Bij=Bi+1,j+1=B(i-j+1),1,i=1,2,…,n;j=1,2,…,i-1。
(10)
2 破碎参数计算
2.1 试验结果
不同磨矿时间下的磨矿产物粒度分布见表2,不同磨矿时间下的磨矿产物各粒级产率变化如图1所示。

表2 不同磨矿时间下的磨矿产物粒度分布Tab.2 Particle size distribution of grinding products in different grinding time %

图1 不同磨矿时间下的磨矿产物各粒级产率变化Fig.1 Yield changes of grinding products at different grinding time
由表2和图1可知,随着磨矿时间的增加,-0.425+0.300、-0.300+0.212、-0.212+0.150 mm这3个粒级产率呈指数规律减小;-0.075 mm粒级产率呈线性规律增大,-0.106+0.075 mm粒级呈先增大后减小的趋势。
2.2 一阶磨矿动力学模型
一阶磨矿动力学模型是基于类似化学反应动力学方程所建立,
R=R0exp(-kt),
(11)
式中:R、R0分别为给料和产品中粒级的筛上累积产率;k为与物料性质有关的参数;t为磨矿时间。
将式(11)变形,令y=ln(R0/R),可线性转化为
y=kt+b。
(12)
根据式(12)对不同粒级的磨矿试验结果进行线性拟合,拟合结果见表3和图2所示。

表3 磨矿动力学拟合结果Tab.3 Fitting results of grinding kinetics

图2 磨矿动力学拟合曲线Fig.2 Fitting curve of grinding kinetics
由表3和图2可知,在磁铁矿批次磨矿中,不同粒级物料的磨矿过程均符合一阶磨矿动力学模型。随着粒度的减小,所拟合直线的斜率减小,说明粗粒级相比细粒级具有更高的破碎速率。磨机中物料的破碎速率与其粒度大小有关,粒度越小,在磨矿过程中被选择的概率越低,其消失速率更慢;粒级越大,在磨矿过程中与磨矿介质和衬板的有效接触面积越大,消失速率更快。
2.3 计算破裂分布函数bij
基于不同磨矿时间的批次磨矿试验结果分别计算Bij,然后取其平均值。当j=1时,由式(9)对Bi1进行计算,Bi1结果见表4。

表4 不同磨矿时间下的Bi1值Tab.4 Bi1 values at different grinding time
对于规范化的破裂分布函数,有bij=Bij-Bi+1,j,因此由表4可计算出破裂分布函数的第一列的值bi1,进而计算其他各列的值,bij计算结果见表5。

表5 破裂分布函数bij的值Tab.5 Values of crushing distribution function bij
2.4 计算选择函数S
基于不同磨矿时间的批次磨矿试验结果,由式(7)分别计算S,然后取其平均值,不同磨矿时间下的S值计算结果见表6。

表6 不同磨矿时间下的S值Tab.6 S values at different grinding time
3 磨矿产物粒度组成预测
基于磨矿总体平衡动力学模型,使用MATLAB中的Simulink模块对式(3)进行建模,可实时仿真预测出磨矿产品粒度分布。模型中包含的模块为:1个常数模块——给矿;2个增益模块——换算百分含量;2个显示模块——给矿粒度分布、磨矿产物粒度分布;1个子系统模块——实验室球磨机;1个输出模块——磨矿产物。其中子系统模块用来设置破裂函数矩阵b和选择函数矩阵S并进行运算。设置仿真时间并运行仿真模型即可从显示模块观察到磨矿产物的各粒级产率分布。将前面计算所得的破碎参数S、bij及给矿粒度分布f输入到所建立的Simulink模型中,分别设定仿真时间t为4、8 min,进行仿真运算并得到磨矿产物粒度组成,预测结果见表7。

表7 磨矿产物粒度组成预测结果Tab.7 Thepredicted results of particle size composition of grinding products %
由表7可知,磨矿产物各粒级的预测值与试验值均相近。不过,预测磨矿时间4 min的结果时,在-0.075、-0.15+0.106 mm粒级预测的绝对误差较大,分别为3.21%和3.00%;在-0.425+0.3 mm粒级预测的相对误差最大,为24.21%。预测磨矿时间8 min的结果时,在-0.212+0.15 mm粒级预测的绝对误差和相对误差最大,依次为0.65%和14.98%。与磨矿时间4 min相比,磨矿8 min的绝对误差之和与相对误差之和均较小,预测精度相对较高。
4 结论
①混合物料的磁铁矿批次磨矿过程符合一阶磨矿动力学模型,各粒级物料的磨矿速度与其粒度大小有关。
②根据批次磨矿结果,可以采用BII算法计算求解总体平衡模型中的破裂分布函数和选择函数,并借助Simulink构建总体平衡仿真模型,进行预测磨矿产物粒度组成。
③磨矿产物各粒级的预测值与试验值均相近。不过,预测磨矿4 min的结果时,在-0.075、-0.150+0.106 mm粒级预测的绝对误差较大,分别为3.21%和3.00%;在-0.425+0.300 mm粒级预测的相对误差最大,为24.21%。预测磨矿8 min的结果时,在-0.212+0.150 mm粒级预测的绝对误差和相对误差最大,分别为0.65%和14.98%。与磨矿4 min相比,磨矿8 min的绝对误差之和与相对误差之和均较小,预测精度相对较高。

