频变耦合双通带滤波器的综合方法
李 刚
(湖北文理学院 物理与电子工程学院,湖北 襄阳 441053)
随着无线技术的发展,多种通信制式并存的情况将持续一段时期,这也对微波滤波器的性能指标提出了更加严苛的要求,因此能够同时实现两个通带特性的双通带滤波器引起了业界的广泛关注。文献[1~2]采用多模谐振腔实现了双通带滤波器,但该方法要求两个通带的谐振模式必须同时谐振,这给滤波器的设计和后期调试带来了困难。文献[3~4]通过频率变换技术获得双通带滤波器的特征多项式,然后再应用经典的耦合矩阵综合方法,可一次性得到双通带滤波器的全部耦合系数等设计信息。但该方法中,滤波器的有限传输零点受所有谐振腔的控制,滤波器的后期调试耗时费力。以上双通带滤波器实现技术的共同特点是谐振腔之间的耦合为非频变耦合。近年来,能够实现有限传输零点的频变耦合滤波器受到研究者们的广泛关注[5-10]。在实现同样的有限传输零点条件下,相比传统交叉耦合滤波器,频变耦合滤波器拓扑结构简单,后期调试更便捷。
为了解决频变耦合双通带滤波器缺少有效综合方法的问题,本文提出了一种优化综合方法。该方法首先通过频率变换技术得到滤波器在归一化双通带域内的特征多项式。然后,该方法应用经典的耦合矩阵综合方法算出双通带滤波器的全规范耦合矩阵,进而以矩阵的特征值为趋近目标构造目标函数。最后,应用梯度优化算法进行优化即可获得双通带滤波器的频变耦合矩阵。
1 综合理论
1.1 频率变换

(a)
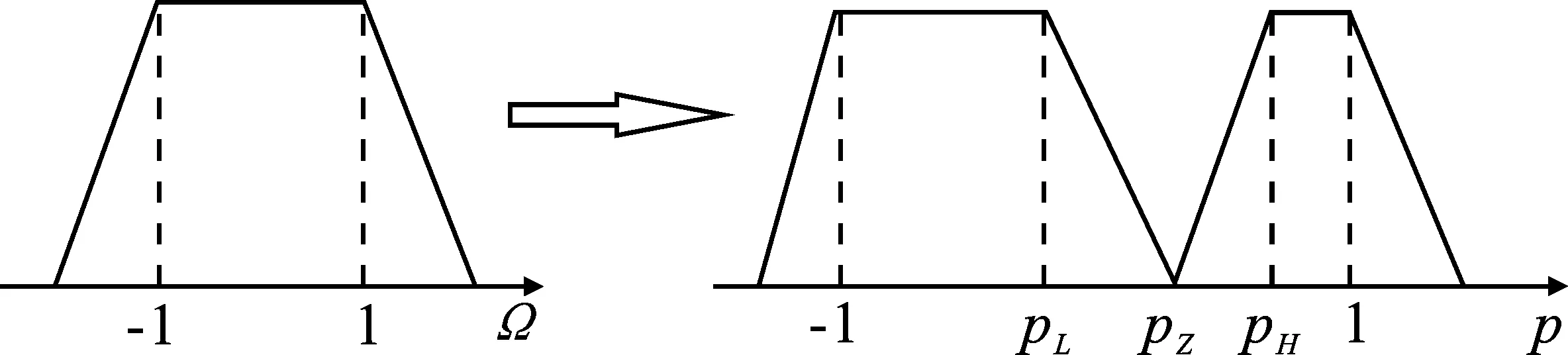
(b)图1 频率映射关系 (a)实际频域到归一化双通带域映射关系(b)归一化低通域到归一化双通带域映射关系Figure 1. The frequency mapping (a)Mapping relationship from actual frequency domain to normalized dual-band domain(b)Mapping relationship from normalized low pass domain to normalized dual-band domain
假设双通带滤波器具有两个非对称的通带,通带对应的角频率范围为(ωL1,ωH1)和(ωL2,ωH2),ωZ是分隔两个通带的有限传输零点。根据式(1),可以建立实际角频率域到归一化双通带域之间的频率变换关系
(1)
式中,ω是实际频域的角频率变量;p是归一化双通带域的角频率变量;b1和b2是待定常数。

表1 ω域与p域映射关系
将表1所示的具体频点映射关系带入式(1),对方程求解后可得式(2)。
(2)
从归一化低通域到归一化双通带域的频率变换关系为
(3)
式中,Ω是归一化低通域的角频率变量;p是归一化双通带域的角频率变量;e1~e4是待定常数;pZ是归一化双通带域中分隔两个通带的有限传输零点,pZ=0对应对称型双通带情况,否则对应非对称型双通带情况。

表2 Ω域与p域映射关系
将表2所示的具体频点映射关系带入式(3),解方程可得关系式(4)。
(4)
在已知双通带滤波器设计指标前提下,根据式(1)~式(4)便可以求得归一化双通带域下的特征多项式。
1.2 目标函数
根据频率变换技术,在得到双通带滤波器的特征多项式后,根据经典耦合矩阵综合方法[11-18]可求得滤波器的全规范耦合矩阵Mtrans,具体为
(5)

f= (λtrans-λfinal)T(λtrans-λfinal)
(6)
式中,λfinal对应矩阵Mfinal的本征值;λtrans对应矩阵Mtrans的本征值。针对上述目标函数,应用梯度优化算法Solvopt进行优化,便可得到指定拓扑结构的频变耦合矩阵。图2所示为频变耦合滤波器优化综合流程图,频变耦合矩阵优化步骤可参考文献[9~10]。
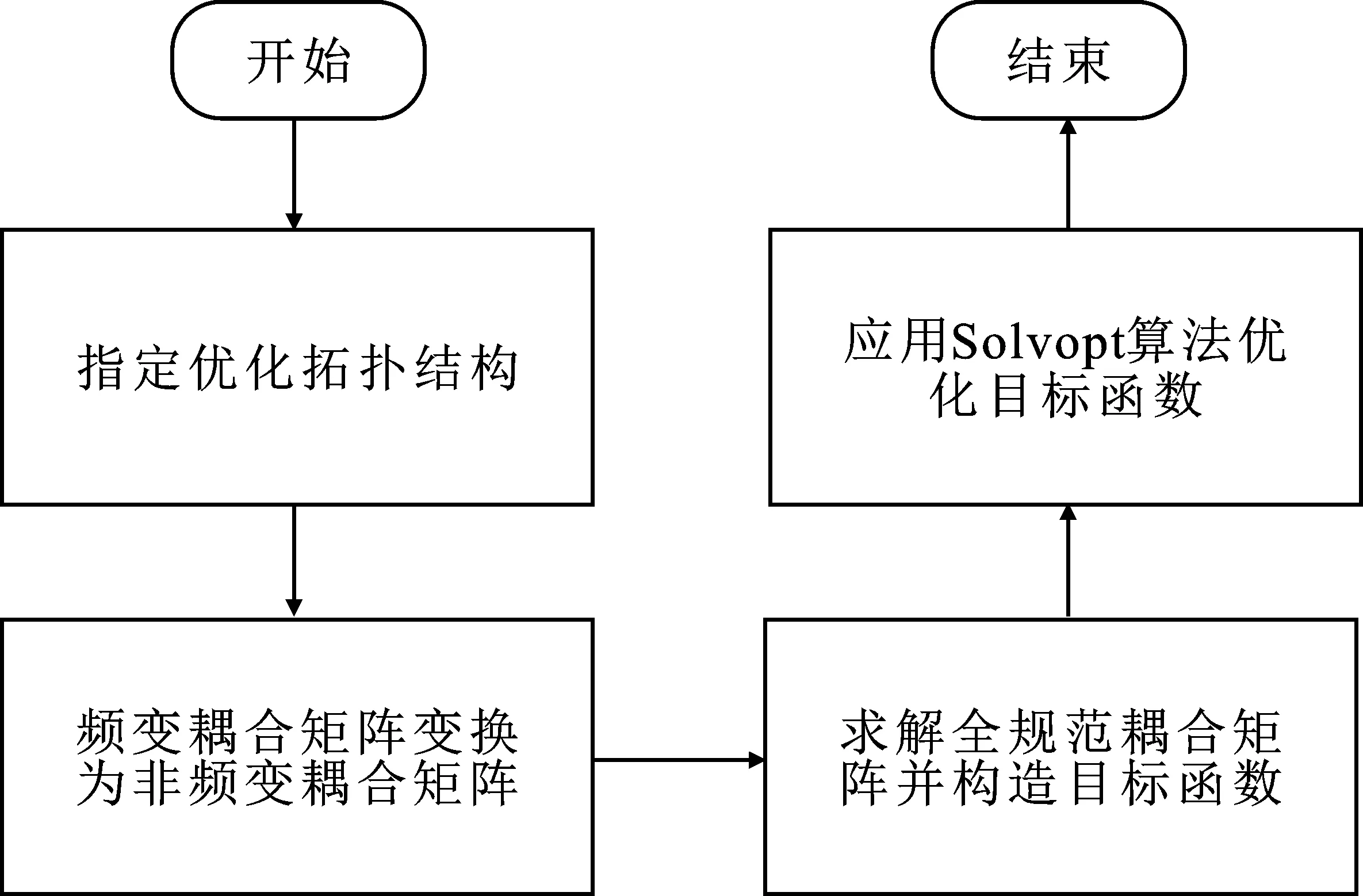
图2 优化流程图Figure 2. Flow chart of the optimization
基于上述理论分析,频变耦合双通带滤波器的综合设计步骤为:
步骤1根据双通带滤波器工作频率范围,应用式(2),求出实际频率域和归一化双通带频率域映射关系中的待定常数;
步骤2指定有限传输零点,选择广义切比雪夫函数,求出归一化低通域下的有限传输零点和反射零点。应用式(4),求出归一化双通带频率域下的传输零点和反射零点,进而确定双通带滤波器的特征多项式;
步骤3根据双通带滤波器的特征多项式,应用经典的耦合矩阵综合法,求出滤波器的全规范耦合矩阵;
步骤4指定频变耦合拓扑,应用式(6)所示的目标函数进行优化,得出双通带滤波器的频变耦合矩阵。
2 综合实例
为验证所提方法的有效性,本文针对对称型和非对称型双通带滤波器进行优化综合。
2.1 综合对称型频变耦合双通带滤波器
第一通带频率范围为840~855 MHz,第二通带频率范围为884~899 MHz,滤波器阶数n=8,回波损耗RL= 20 dB,有限传输零点频率为830 MHz、858 MHz、869 MHz、880 MHz、910 MHz。

(a)

(b)图3 对称型双通带滤波器拓扑及频率响应 (a)直线型滤波器拓扑 (b)滤波器频率响应Figure 3. Topology and frequency responses of the symmetric dual-band filter(a)In-line filter topology (b)Filter frequency responses
双通带滤波器的第一通带和第二通带的带宽均为15 MHz,属于对称型双通带滤波器。本文选择如图3(a)所示的直线型频变耦合拓扑,其中带箭头耦合为频变耦合,不带箭头耦合为非频变耦合。应用文中综合步骤,求得归一化双通带域参数pL=-0.5,pH=0.5,pZ=0;归一化低通域有限传输零点为Ω=-2,Ω=2。归一化耦合系数MS1=0.609 8,M12=0.277 7Ω- 0.827 2,M23=-0.010 7Ω+ 0.031 7,M34=0.996 9Ω+0.411 9,M45=0.028 9,M56=0.119 3Ω- 0.355 1,M67=0.197 3Ω- 0.587 0,M78= 0.292 0Ω- 0.868 5,M8L=-0.599 5,M11= -0.377 5,M22=-0.229 1,M33=0.437 8,M44=0.384 4,M55=0.477 6,M66=-0.497 9,M77=-0.539 4,M88=-0.380 5。
图3(b)为直线型频变耦合双通带滤波器的频率响应。由图可知,两个通带内均保持了等波纹特性。直线型频变耦合拓扑中有6个频变耦合,频率响应曲线中出现了5个有限传输零点,其原因是有限传输零点869 MHz是二阶有限传输零点,其余零点均为一阶有限传输零点。
2.2 综合非对称型频变耦合双通带滤波器
第一通带频率范围840~863 MHz,第二通带频率范围881~899 MHz,滤波器阶数n=8,回波损耗RL=20 dB,有限传输零点频率为816 MHz、868 MHz、873 MHz、878 MHz、924 MHz。

(a)
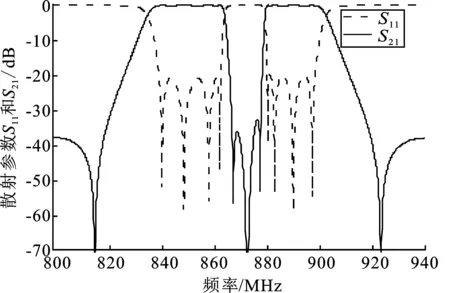
(b)图4 非对称型双通带滤波器拓扑及频率响应 (a)直线型滤波器拓扑 (b)滤波器频率响应Figure 4. Topology and frequency responses of the asymmetric dual-band filter(a)In-line filter topology (b)Filter frequency responses
双通带滤波器的第一通带的带宽为23 MHz,第二通带的带宽均为18 MHz,属于非对称型双通带滤波器。选择如图4(a)所示的直线型频变耦合拓扑,其中带箭头耦合为频变耦合,不带箭头耦合为非频变耦合。应用文中综合步骤,求得归一化双通带域参数pL=-0.2,pH=0.4,pZ=0.15。归一化低通域有限传输零点为Ω=-2,Ω=2.4。归一化耦合系数MS1=0.256 2,M12=0.274 2Ω+0.032 6,M23=0.958 0Ω- 0.387 0,M34=-0.004 6Ω+0.073 6,M45=0.058 5,M56=0.993 6Ω-0.127 1,M67=-0.003 8Ω+ 0.061 5,M78=-0.051 3Ω+0.826 1,M8L=0.869 7,M11=0.155 1,M22=-0.376 4,M33=-0.391 9,M44=-0.001 8,M55=-0.174 0,M66=-0.080 6,M77= -0.116 7,M88=-0.021 6。
图4(b)为直线型非频变耦合双通带滤波器的频率响应。由图可知,两个通带内均保持了等波纹特性。直线型频变耦合拓扑中有6个频变耦合,频率响应曲线中出现了5个有限传输零点,原因是有限传输零点873 MHz是个二阶有限传输零点,其余零点均为一阶有限传输零点。
由对称型和非对称型频变耦合双通带滤波器的综合实例可知,本文方法在双通带域内均能够较好地保持等波纹特性。频变耦合拓扑的应用也使得直线型拓扑能够实现有限传输零点。每个一阶有限传输零点对应一个频变耦合,每个二阶有限传输零点对应两个频变耦合。
3 结束语
本文提出了一种频变耦合双通带滤波器的优化综合方法。通过两次频率变换,建立归一化双通带域与归一化低通域之间的关系,以此求出双通带滤波器的特征多项式,进而应用耦合矩阵综合和优化方法,得到双通带滤波器的频变耦合矩阵。本文通过对称型和非对称型双通带滤波器的数值优化算例验证了所提方法的有效性和正确性。结果表明:(1)该算法能够较好地保持双通带带宽内的等波纹特性;(2)直线型频变耦合拓扑可以方便地实现双通带滤波器;(3)频变耦合可以实现一阶和二阶有限传输零点。本文方法给频变耦合双通带滤波器的工程实践提供给了灵活的拓扑选择,具有重要的工程价值。

