一种新型悬浮磁体结构的双自由度轨道车辆轴箱振动能量采集器
李哲辉,袁天辰,杨 俭,宋瑞刚
(上海工程技术大学 城市轨道交通学院,上海 201620)
在轨道车辆中,轴箱是套在轴颈上联结轮对和转向架或二轴车车体的关键部件,其作用是将车体重量传递至轮对上,润滑轴颈,降低摩擦热损耗。一旦轴箱出现故障将引发热轴故障,严重时车辆将出现切轴事故,直接导致人员伤亡和财产损失。温度是旋转机械健康状况的重要指标,所以轴箱轴承温度状态对于轨道车辆的故障预测和健康管理非常重要[1]。
随着传感技术的发展, 传感系统在监测物理参数(温度、速度和机械压力等)的应用中越来越重要[2]。目前,地铁列车轴箱温度检测系统装置中包括一个电子标签和与之连接的温度探头。电子标签安装在地铁车辆轴架上,温度探头通过轴箱紧固螺栓固定在轴箱端盖上。轴温检测电子标签采用高温锂电池供电,但由于锂电池无法承受轴箱严苛的振动环境且电池的体积和重量较大,因此电子标签主体无法通过小型化设计直接安装在轴箱上,其只能被安装在列车轴架上。同时,由于温度探头也需要固定在轴箱上,因此还需要在轴架和车体上进行复杂的布线[3]。这使得维保人员对已安装到列车上的轴温检测装置进行电池更换作业和日常维护十分费时费力,因此针对具有自供电功能的无线传感器终端设备进行研究具有重要意义[4]。
收集环境能源作为电池的补充,可有效延长无线节点的使用寿命[5-6],这也为取代传统电池提供了方法参考。在自供电功能的终端设备研究方面,文献[7]中设计了一种带有哈巴赫矩阵排列的强磁振子磁悬浮式能量俘获装置。该发电系统在振动频率为35 Hz且振幅为130 mm的激励下,理论输出电能为2.15 V。文献[8]提出了EM-VEH结构的电磁式振动能量采集器,并验证了其为桥梁变采集单元或GPS数据传输供电的可行性。研究发现,其功率密度峰值为176.5 μW·cm-3。文献[9~10]提出利用轨道振动驱动单自由度磁浮式电磁振动换能器获取能量,若配合储能电池使用,则可以为轨旁铁路检测设备进行供电。
由于地铁运行环境的限制,在高架或隧道内安装轨旁红外测温探头较为困难[11]。采用结构简单、体积小、可车载的地铁车辆轴温实时监测系统终端供电设备可解决这一问题。因此,本文提出了一种磁悬浮式轨道车辆轴箱双自由度振动能量采集器。该采集器俘获轨道列车轴箱的振动能量,并将其转化为电能来为轴箱附近的电子标签或无线传感器节点供电,降低了电子标签及无线传感系统对传统锂电池的依赖性。
本文首先介绍磁悬浮式双自由度振动能量采集器的结构模型以及工作原理;然后,分析振动能量采集器环境激励;最后,利用COMSOL软件构建振动能量采集器的有限元模型并对其进行频域、时域的仿真分析,根据仿真结果对振动能量采集器进行结构改进优化,为振动能量采集器的实物设计提供依据。
1 磁悬浮式振动能量采集器结构描述
磁悬浮式双自由度轴箱振动能量采集器的主要部件包括与轴箱连接的弹性框架、两块固定的轴向磁化永磁体、一块复合式悬浮磁铁以及缠绕固定于框架外部的铜线圈。结构示意图如图1所示。复合式悬浮磁体结构由两块轴向磁化圆柱形磁体和一块圆柱形铜块组成,其磁感应强度如图2所示。
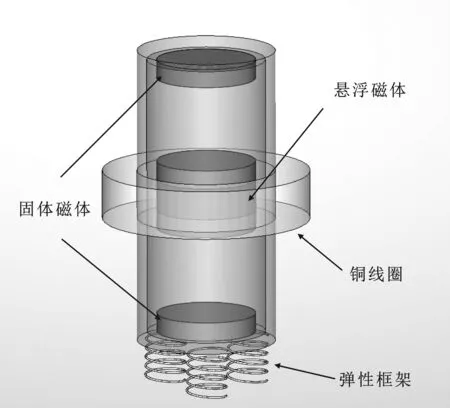
图1 磁悬浮式振动能量采集器结构示意图Figure 1. Schematic diagram of the structure of the magnetic levitation vibration energy harvester

图2 复合式悬浮磁体结构磁感应强度(部分剖面)Figure 2. Magnetic induction intensity of composite suspension magnet structure (partial section)
本文设计的磁悬浮式双自由度振动能量采集器为铁圈同振型结构。该结构利用磁铁间的电磁力代替机械弹簧,即当振动能量采集器受到轴箱垂向振动激励时,悬浮磁体、框架均可在各自的平衡位置附近振动,且二者之间存在相对运动,使得铜线圈中的磁通量产生变化。依据电磁感应定律,线圈中就会产生感应电流,负载电阻上会产生感应电动势,从而将振动能量转化为电能输出。该设计中磁性弹簧结构拥有较小的摩擦和损耗[12],且不会因材料疲劳而引起结构失效,因此悬浮磁铁结构可以使振动能量采集器拥有更长的使用寿命。
2 振动能量采集器工作环境激励分析
2.1 轨道车辆轴箱激励分析
对轨道车辆轴箱的分析是设计轴箱振动能量采集的基础。地铁正线的轨道谱总体特征趋势相类似[13],地铁列车运行正线由多个站间区间构成,周期性的区间特性可表征正线的连续运行特性,因此本文基于上海地铁列车在某一站间区间内运行所测得的轴箱垂向振动信号展开针对性研究,进行磁悬浮式振动能量采集器的参数设计。该垂向振动加速度信号时间历程共114 s,如图3所示。

图3 车辆轴箱垂向振动加速度时间历程Figure 3. Time history of vertical vibration acceleration of vehicle axle box

图4 车辆轴箱垂向振动加速度信号频谱图Figure 4. Frequency spectrum of vertical vibration acceleration signal of vehicle axle box
轨道车辆轴箱的频率特性决定了振动能量采集器的主要设计参数。将车辆轴箱垂向振动加速度信号进行傅里叶变换,得到车辆轴箱垂向振动加速度信号频谱图,如图4所示。从图4中可以观察到,在城市轨道交通的轨道不平顺作用下,轴箱可能有多阶模态被激发,导致频带分布较广泛,因此宜采用双自由度振动能量采集器的宽频工作特性。其中,地铁车辆轴箱垂向振动激励峰值频率为f1=33.94 Hz和f2=58.22 Hz,故应将本文振动能量采集器的固有频率控制在58.22 Hz及33.94 Hz附近。此时外界主要激励频率与振动能量采集器固有频率相近,可引起采集器共振效应,使得悬浮磁铁的相对振动速度变大,提升俘能效果。
2.2 振动能量采集器工作环境激励分析
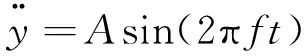
(1)
式中,A为基础激励的振幅;f为基础激励的振动频率。
振动加速度有效值即振动加速度的均方根(Root Mean Square,RMS),可被直接用来反映振动的能量。令w=2πf,对一段周期时间t内的外界加速度激励求其加速度有效值。
(2)
对图3中车辆轴箱垂向振动激励时间历程进行统计分析,得其振动幅值的均方根值为2.682 m·s-2。令基础激励振幅的有效值与车辆轴箱振动激励振幅均方根值相等,进而达到等效替代的目的。
(3)
计算得出A=3.793 m·s-2,故本文振动能量采集器中采用等效外界基础加速度激励幅值为3.793 m·s-2。
3 振动能量采集器有限元模型建立
3.1 永磁体间磁力模型构建
文献[14~16]给出了永磁体之间受力的理论关系式,但是这些关系式并不是显式且过于复杂,不便于进行振动能量采集器动力学响应分析[17]。因此,本文采用COMSOLTM有限元仿真并结合数值拟合的方法来获得电磁力及等效电磁力构成的磁性弹簧刚度。
本文选用规格为D10 mm×2 mm的钕铁硼圆柱永磁铁(NdFeB N-35),其密度为7.5×103kg·m-3,永磁体剩余磁通密度为1.18 T。永磁体间磁力模型通过COMSOL软件选择“AC/DC模块”中的“磁场,无电流”项建立有限元模型。
静态磁场方程为
∇×H=J
(4)
式中,∇为梯度;H为磁场;J为电流密度。
在无电流区域,电流密度为0,故
∇×H=0
(5)
进而定义标量磁势为Vm,则
H=-∇Vm
(6)
结合磁通密度与磁场之间的本构关系、高斯磁定律,推导得无电流磁场边界条件为
(7)
式中,B为磁感应强度;M为磁化强度;μ0为真空中的磁导率;μr为相对磁导率。
本模型使用“零磁标量势”条件作为二维轴对称的边界条件,在反对称平面上,磁场与边界垂直,则有
n·B=0
(8)
式中,n为法向向量。
由于在空间场中磁场的分布是无边界的,所以需要在有限元模型中设定空气域是无限元域。空气域是一个直径为两磁体模型尺寸4倍大小的球状结构,无限元域为空气域外厚10 mm的球层,如图5所示。
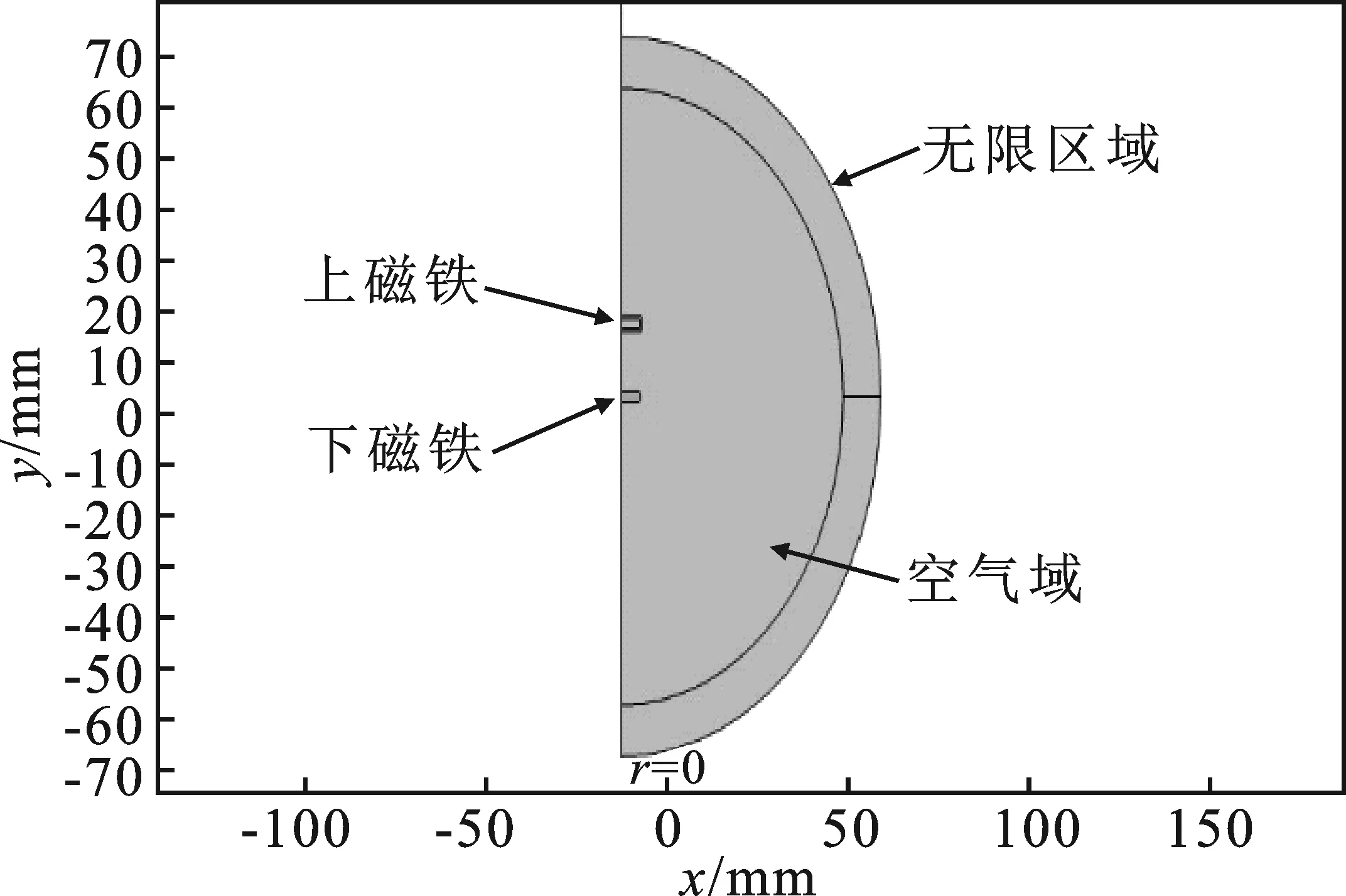
图5 两圆柱永磁体间磁力计算模型Figure 5. Magnetic force calculation model between two cylindrical permanent magnets
通过自由三角形网格和映射网格对永磁体间磁力模型进行了更加细化的网格划分,如图6所示。
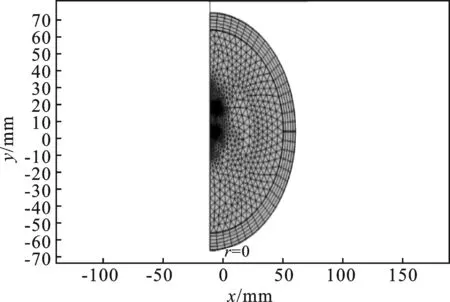
图6 两圆柱永磁体间磁力模型网格划分Figure 6.Mesh division of the magnetic force model between two cylindrical permanent magnets
作用在磁体外表面上的电磁场会发生跃变。通常用来确定磁体所受电磁力的一种方法就是将这种跃变产生的应力进行集中处理。应力可以通过使用麦克斯韦表面应力张量表示,故上磁铁所受到下磁铁的电磁力可通过上磁铁所有外部边界上的麦克斯韦表面应力张量积分进行计算确定。计算表达式为
(9)
式中,r为磁体半径;S为磁体表面积;Ω为磁体体积;T为空气的应力张量。
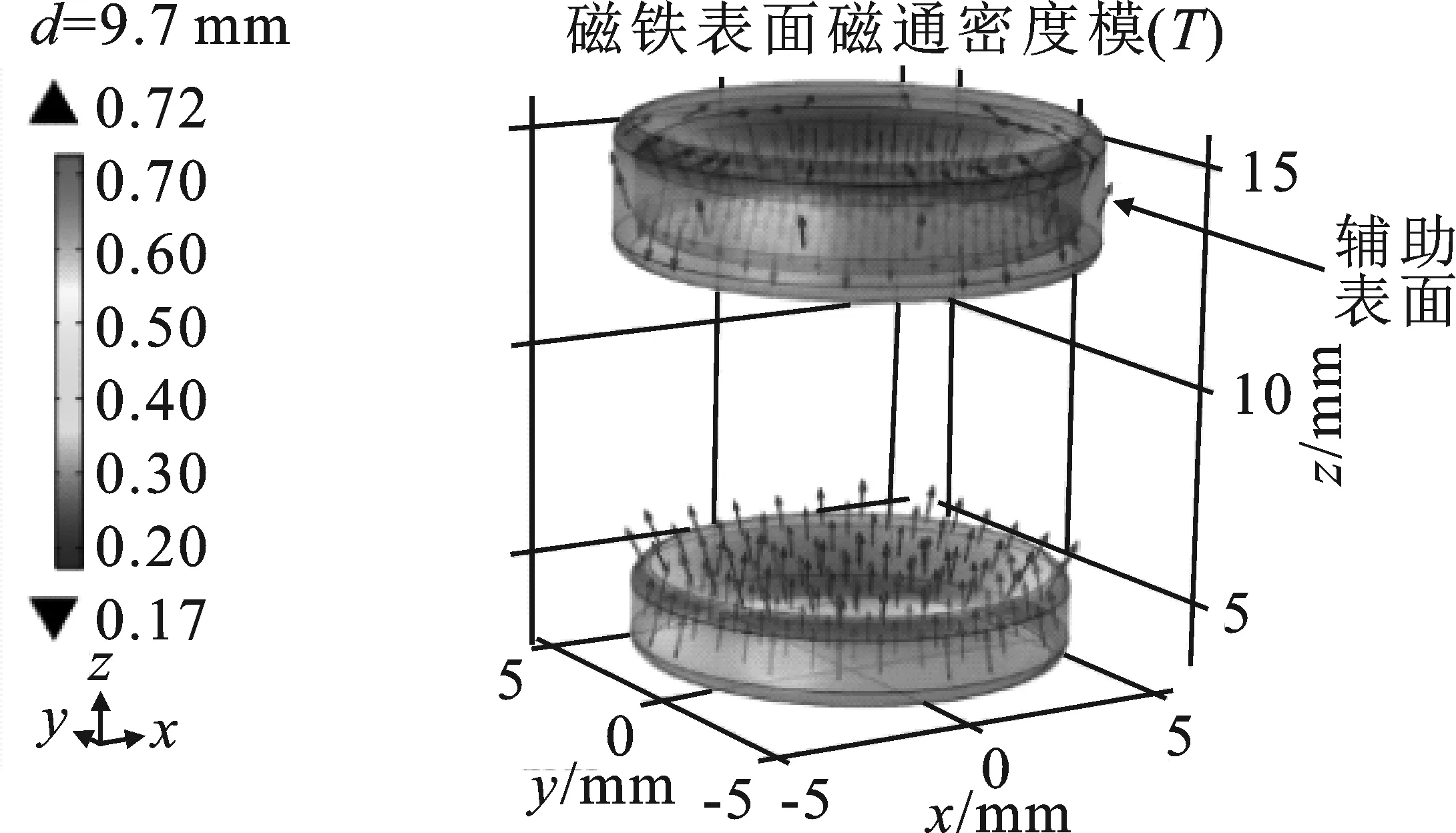
图7 磁体表面磁通密度模(三维图)Figure 7. Magnetic flux density model on the surface of the magnet (three-dimensional image)

图8 磁体表面磁通密度模(二维剖面图)Figure 8. Magnetic flux density model on the magnet surface (two-dimensional cross-sectional view)
由于磁体附近的磁场高度集中,所以应力张量也高度集中。因此,进入边界积分的量只集中在少数网格单元中,而其他网格位置量的值则接近于零。但是,磁极附近发生的奇异行为在一定距离内会逐渐消失。本文提出引入一个辅助表面,将其置于上磁体的周围并保持一定的距离,从而增加数值精度,如图7和图8所示。
通过“参数化扫描”接口对两永磁体之间多个距离进行扫描,求得上磁体所受下磁体的电磁力随磁体间间距变化的曲线,如图9所示。由图可知,在使用辅助表面后,应力张量可以取得较好的效果,电磁力精度也得到了显著提高。

图9 电磁力变化曲线Figure 9. Electromagnetic force variation curve
通过求导解析电磁力曲线,得到两磁体间等效磁性弹簧刚度变化曲线,如图10所示。

图10 磁性弹簧刚度变化曲线Figure 10.Curve of stiffness change of magnetic spring
3.2 振动能量采集器集总机械系统模型
本文基于弹簧-阻尼器集总机械系统模型构建双自由度振动能量采集器力学模型,并分析了具有两个自由度的振动能量采集器集总系统模型,其中包含框架与轴箱和固定于框架内部的上下磁体与悬浮磁体间的相互作用。通过使用集总机械系统接口的弹簧、阻尼器、外部源、自由节点等节点对包括磁铁、框架和轴箱在内的能量采集器系统进行建模。其中,弹簧和阻尼器单元表示不同物体间的刚度及阻尼属性,外部源节点和自由节点用于将能量采集器的集总机械系统模型的力学特性与固体力学中边界载荷接口相耦合。振动能量采集器集总机械系统模型如图11所示。

图11 振动能量采集器集总机械系统模型Figure 11. Lumped mechanical system model of vibration energy harvester
图中,k1和k2分别表示悬浮磁体与上、下固定磁体的磁性弹簧刚度,k表示框架弹性刚度,c1和c2表示悬浮磁体与上、下固定磁体间的阻尼系数,c表示框架系统阻尼系数,数字标识表示各外部源节点和自由节点。
3.3 振动能量采集器机电耦合模型
3.3.1 固体力学
考虑到俘能装置整体为三维圆柱结构,为了简化并减小求解规模,本文在几何建模时使用二维轴对称模型来优化计算模型。

图12 振动能量采集器二维轴对称模型Figure 12.Two-dimensional axisymmetric model of vibration energy harvester
本文中,最终求解目标仅是线圈中的感应电流。此电流通过域上的场积分计算得到,对场中的奇异性极不敏感,故不需要担心几何模型的尖角所引入的局部奇异性问题。为了简化网格划分并便于振动能量采集器的仿真计算,仿真模型中的各磁体和线圈均由矩形体素表示,如图12所示。
3.3.2 磁场
在磁场接口中,定义每块磁体的轴向剩余磁通量为1.18 T,相邻磁体的充磁方向相反。此处给出悬浮磁铁处于中间位置时,模型周围的磁感应强度和磁感线分布,如图13所示。
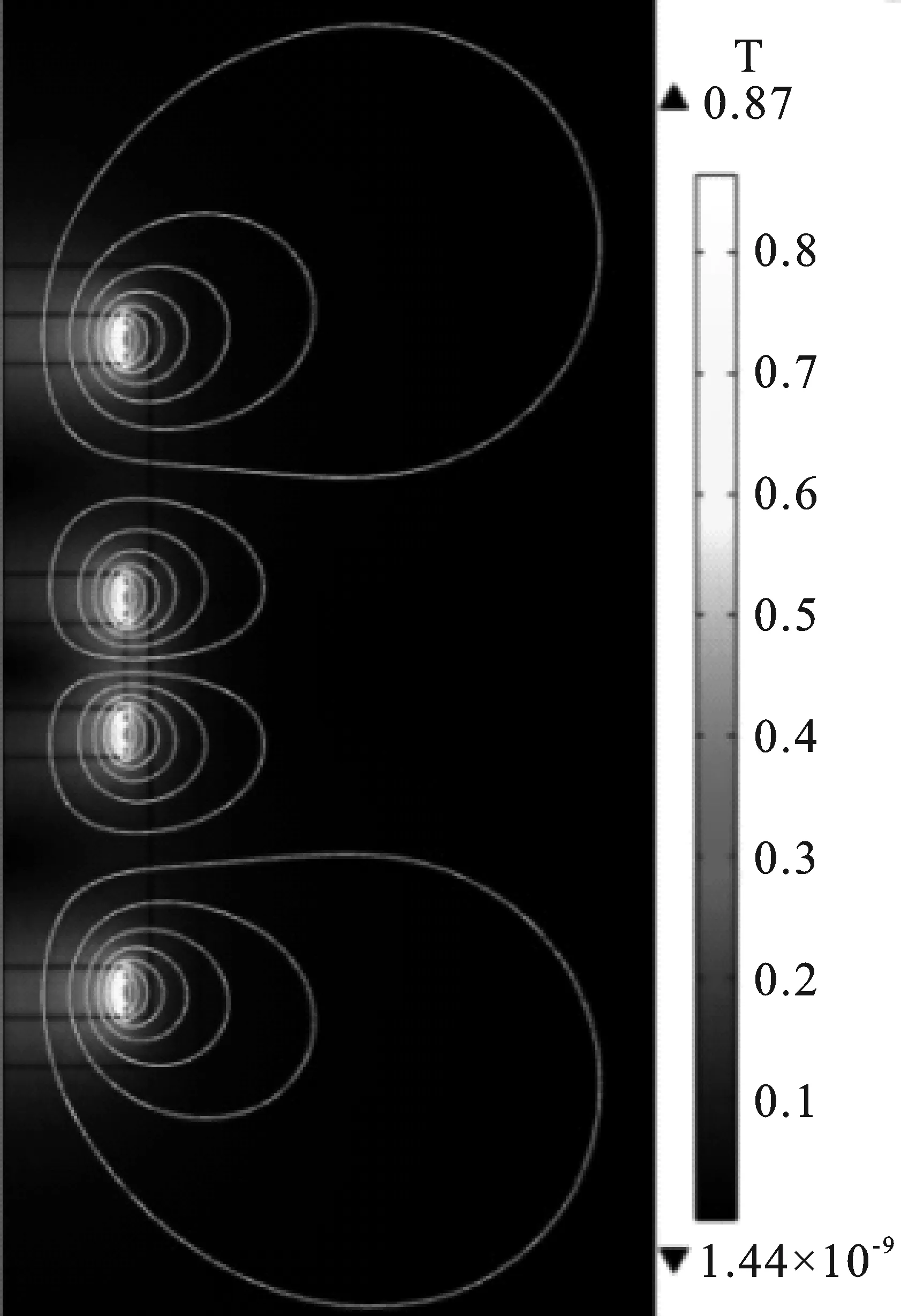
图13 中间位置时磁感应强度/磁感线的半剖面Figure 13.Half section of magnetic induction intensity/lineof magnetic induction in the middle position
3.3.3 电路
磁悬浮式振动能量采集器的电学模型可以看作由一个电压源Vem、感应线圈内阻Rcoil、感应线圈的电感Lcoil和外接负载电阻Rem串联而成的电路,Rem接在输出端,如图14所示。
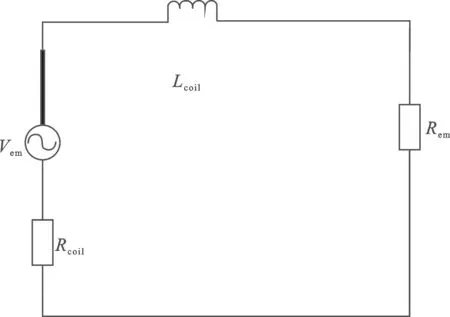
图14 俘能装置等效电路图Figure 14.Equivalent circuit diagram of energy capture device
感应线圈的内阻、垂直方向高度、水平方向宽度等因素与输出电动势的大小均有密切关系。铜线长度越短,线圈内阻越小,消耗的功率越少,电感越小,对输出的电流影响会越小;铜线长度越长,线圈高度越高、宽度越宽、匝数越多,通过线圈的磁通量也越多。本文经参数化扫描线圈内径、线圈垂直高度、水平宽度,通过仿真计算得到线圈最佳标准直径为0.29 mm,线圈垂直高度为5.22 mm,线圈水平宽度为3.19 mm,线圈总匝数为198匝,铜线总长10.8 m,电感为0.01 H。通过“线圈几何分析”接口,计算得到线圈内阻为2.7 Ω。根据最大功率传输的相关理论,当负载电阻与线圈电阻相匹配时,可以得到最大的输出功率,故在外界电路中设定外接电阻为2.7 Ω。
4 振动能量采集器集的仿真
根据法拉第电磁感应定律,为了增加输出电性能,要尽可能地增加永磁体的振动速度。若需了解永磁体共振时的振动状态,就必须对拾振系统做模态分析,从而确定系统的振动特性[18]。本模型中,悬浮磁体与固定磁体间的初始距离决定了两者之间磁性弹簧刚度,且会对系统固有频率产生影响。
首先,通过执行特征频率研究来调整磁悬浮式双自由度振动能量采集系统参数,得到振动能量采集器的固有频率为34.047 Hz和58.251 Hz。调整后的参数如表1所示。
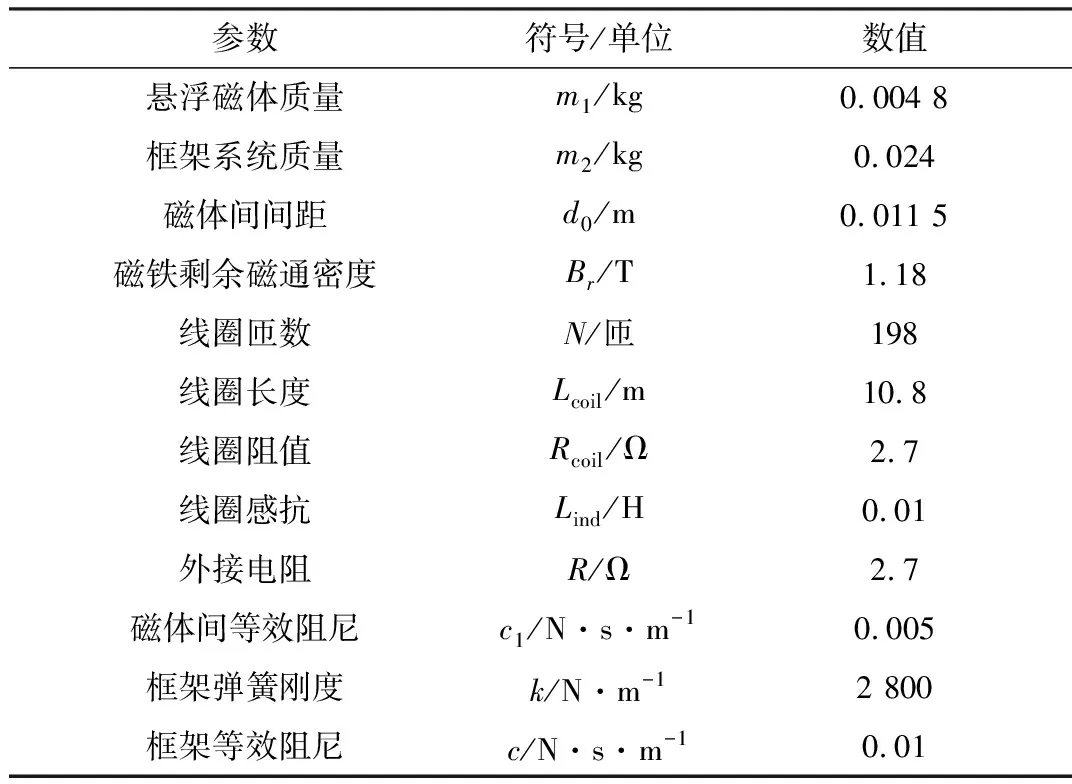
表1 磁悬浮式振动能量采集器主要参数
随后,采用频率范围为30~65 Hz且加速度激励幅值为3.793 m·s-2的线性扰动载荷信号,通过频域扰动测试俘能装置的线性频响特性,如图15所示。由图15可知,在34 Hz的一阶固有频率下,输出功率峰值为2.67 mW;在58.2 Hz的二阶固有频率下,输出功率峰值为4.99 mW。
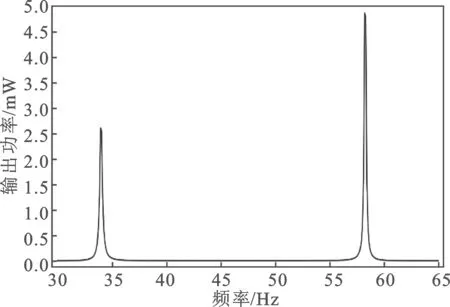
图15 磁悬浮式振动能量采集器频响特性Figure 15.Frequency response characteristics of magnetic levitation vibration energy harvester
5 振动能量采集器的改进
经过上述分析可以看出,铜块-永磁体复合式悬浮磁体结构的俘能系统感应电流及输出功率较小,不利于能量的储存。为了提升能量回收效率,提高感应电流,本文在铜块-永磁体复合式悬浮磁体结构基础上提出一种新型复合式悬浮磁体结构的改进方案,如图16所示。
新型复合式悬浮磁体结构由内圈辐射充磁的环状圆柱磁体上下表面粘合轴向磁化磁体构成,能提供较强的径向磁感强度,如图17和图18所示。在相同振动速度的情况下,新型复合式悬浮磁体相比铜块-永磁体式复合悬浮磁体结构,新型复合式悬浮磁结构体结构能够向感应线圈内提供更多的磁通变化量。根据法拉第电磁感应定律,线圈内也会具有更大的感应电流。
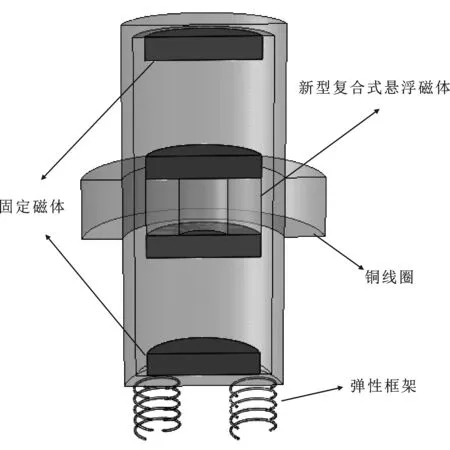
图16 新型复合式悬浮磁体结构(半剖面)Figure 16.Novel composite suspension magnet structure (half section)

图17 内圈辐射充磁磁体磁感应强度(部分剖面)Figure 17.The magnetic induction indensity of inner ring radiating magnetized magnet (partial section)

图18 新型复合式悬浮磁体结构磁感应强度(部分剖面)Figure 18.The magnetic induction intensity of the new composite suspension magnet structure (partial section)
执行频域分析,计算等效简谐振动激励下的振动能量采集器输出电流和输出功率随频率的变化,如图19和图20所示。由图可知,在34 Hz的一阶固有频率下,输出电流峰值为36.7 mA,输出功率峰值为4.48 mW,较改进前提高了68%;在58.2 Hz的二阶固有频率下,输出电流峰值为63.0 mA,输出功率峰值为13.22 mW,较改进前提高了165%。
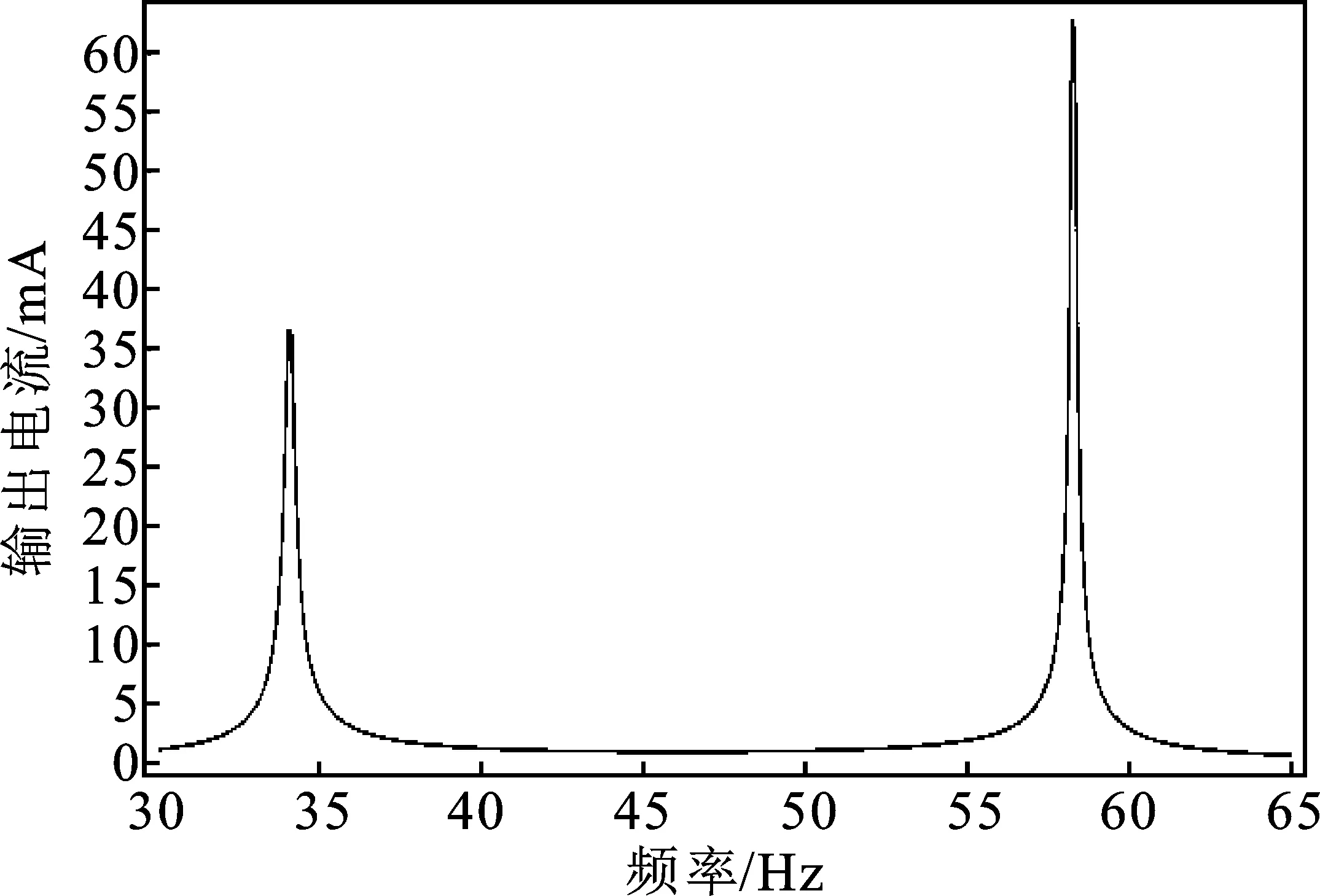
图19 俘能装置输出电流Figure 19.Output current of energy capture device

图20 俘能装置输出功率Figure 20.Output power of energy capture device
执行瞬态分析,计算等效简谐振动激励下的振动能量采集器俘能功率。如图21和图22所示,俘能效果良好,与频域计算结果基本吻合。
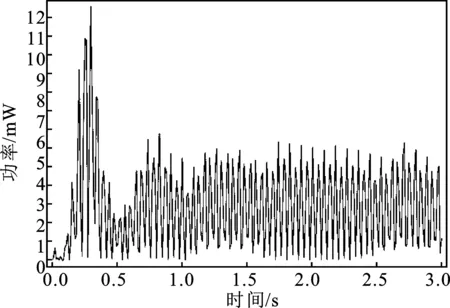
图21 等效简谐振动激励下俘能装置输出功率 (34 Hz)Figure 21.The output power of the energy capture device under equivalent simple harmonic vibration excitation (34 Hz)

图22 等效简谐振动激励下俘能装置输出功率(58.2 Hz)Figure 22.The output power of the energy capture device under equivalent simple harmonic vibration excitation (58.2 Hz)
6 结束语
磁悬浮式双自由度轨道车辆轴箱振动能量采集器通过将轴箱工作环境中普遍存在的振动能转换为电能,来为电子标签、长寿命无线传感网络节点等提供稳定的电源。本文基于轨道车辆轴箱振动激励,分析了磁悬浮式振动能量采集器的工作环境激励,构建了磁悬浮式双自由度振动能量采集器有限元模型,并通过频域场计算和瞬态场计算分析得到以下结论:(1)建立了永磁体间磁力计算有限元模型,通过引入辅助表面可有效提升电磁力计算及等效磁性弹簧刚度计算精度;(2)在58.2 Hz的固有频率激励下,俘能系统峰值输出电流为63.0 mA,输出功率峰值为13.22 mW。相比于铜块-永磁体式复合悬浮磁体结构,在相同激励条件下,新型复合式悬浮磁体结构能向感应线圈内提供更多的径向磁通变化量,使俘能系统输出功率提高了165%;(3)本文建立了基于机械集总系统模型和机电耦合模型并结合多物理场耦合的研究方法,在磁悬浮式双自由度振动能量采集器有限元模型建立中成功应用了该方法。

