考虑节点负荷波动的直流电网暂态电压稳定性自动控制方法

卢志财

(闽南理工学院 实践教学中心，福建 石狮 362700)

随着输电网的不断发展和网络规模的不断扩大，全球大部分输电网络都呈现出1种高负荷运行的态势。近几年，我国特高压和跨区域输电体系得到进一步强化，从能源基地到负载中心的远距离大容量送电模式已经初具规模，但大受端电网的电压崩溃问题越来越突出。同时，由于新能源的大规模接入，工农业生产、生活、负荷的随机变化、自然灾害等因素的存在，使电力系统的运行与规划变得更加困难并具有更多不确定性。因此，有效地解决这些影响电网稳定可靠运行的问题就显得尤为紧迫。电网的不稳定，尤其由电压崩溃所造成局部甚至大规模的、持久的负载损耗，影响电网的可靠性和经济性。在复杂电网中，稳定性对可靠性的影响是一个十分重要的因素，但在电力系统中，无功不足对可靠性的影响还没有引起足够的重视。

在此背景下，许多学者研究了暂态电压稳定性自动控制方法。付媛等研究了柔性直流电网的暂态稳定判据与电压恢复控制技术[1]，该方法首先建立柔性直流电网的动力学模型，通过在负荷和直流电压的变化过程中的运动轨迹进行分析，阐明其稳态工作机制，其次，给出柔性直流系统暂态稳定恢复时必须遵守的等电量原理，并将其与直流电压限制相结合，得出直流系统的暂态稳定准则。赵悦彤等研究了直流电网暂态过电压机理与抑制策略[2]，首先，对电力系统不均衡引起的直接电流通过的机制进行分析，得出直流系统中直流电压和不均衡功率之间的定量关系，在此基础上，提出一种新的抑制直流电压升高的虚拟调速控制方法，并采用2种不同的控制策略，分别对单、双极型2种故障进行分析，最后，以 PSCAD/EMTDC为基础，建立四端 FDC模拟模型，并对3种典型故障进行验证。上述提出的方法虽然能够控制电压，但存在控制效果差的问题，为此本文设计一个考虑节点负荷波动的直流电网暂态电压稳定性自动控制方法。

1 暂态电压分区

将直流输电系统的基本方程记作

(1)

式中，E、δ分别为系统的等位和相位角度，U为 母线电压幅值，Z、θ分别为等值组抗模值和阻抗角。

鉴于直流输电的多种控制模式[3]，本课题仅从电压稳定方面进行了分析，并考虑3种不同的计算方法，如下所示：

1)整流器定电流逆变器定电圧表示为

(2)

式中，ki为逆变站变压器变化比值，Ids为直流电流值，Bc为补偿电容对应的电纳。

2)将整流器定电流逆变器定关断角[4]表示如下：

(3)

式中，rs为逆变器关断角，Xc为逆变器侧方的漏抗值。

3)逆变器定电压值，公式如下：

Pdrs=(Uds-IdsR)Ids，

(4)

式中R为直流线路电阻值。

由于电力系统在运行中不可避免地会发生一些干扰，网络中的每个节点都会发生一定的变化，因此，通过对电网的波动幅度和持续时间的分析[5]，可以将瞬态电压下降区域表示为

(5)

式中，Vi(t)为故障后节点时间的电压值，t0为故障开始的时间，VT为最低需求电压值。

通过对初始分区进行聚类和合并，使整个大系统得到合理划分。聚类是指在相同的分类中，对象之间相互类似，而在不同的分类中，对象相互区别[6]。因此，首先要测量节点瞬时电压的相似程度[7]，选择最常用的欧氏距离来衡量节点瞬时电压相似性：

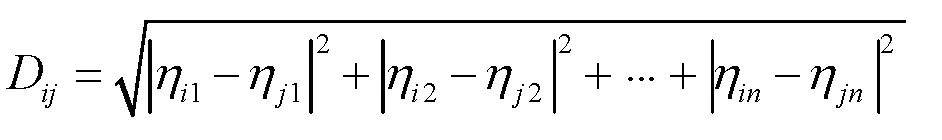
(6)

式中，(ηi1，ηi2，…,ηin)、(ηj1,ηj2,…,ηjm)分别为待分区的节点i、j分别对应的向量。

本文提出的分区聚合算法可以对分区进行细致聚类，但是在聚类前必须先确定最优分区数目。最大分区域的内部距离可以从某种程度上反映出区域的作用[8]，因此，引入基于增量指数标准化指标，以确定最佳分区数目d，其表达式如下：

(7)

在一定的条件下，负载会发生随机的变化，同时，发电机的出力也会发生变化，为此构建跌落矩阵[9]，构建的矩阵如下所示：

(8)

式中m、n分别为节点号与场景号。

依据上述矩阵，将各个节点在不同场景下的瞬态行为分别映射到1个2维平面，并将相邻的节点聚合成一类，同一类型的节点表示该节点的瞬态下 降状况比较类似，并选择其中的代表性节点进行评价。

2 暂态电压稳定的关键影响因素分析

上述过程虽然对数据进行聚类，但是影响暂态电压稳定性的主要特征蕴藏在大量基础测量资料中，为进一步分析影响暂态电压稳定性的关键因素[10]，提取其主要特征，建立输入特征集。在构造输入特征时，首先要考虑电网整体，并结合直流接入，从源、网、荷3个层次分析暂态电压不稳定的产生机制，并由此得出影响直流输电系统暂态电压稳定性的主要因素[11]，主要从下述方面进行分析：

1)电网中的瞬时电压不稳定是指在负载水平高,从远端供电的情况下产生的，受端电网受到较大干扰后，发电机常常会出现过励磁现象，影响电网的稳定运行。无功补偿通常采用就地均衡方式，不能依赖于远端供电[12]，从而进一步造成暂态电压不稳定。

2)电网侧的瞬变电压不稳定。电网瞬时电压不稳定是指当电网的参数发生改变而使其失去平衡时，其实质是以电网的传输极限容量为电压不稳定的临界值[13]。采用曲线来分析系统的电压稳定性(图1)。

当电网受到较大干扰时，其特征曲线将不再与原负载特征相交叉，从而使系统电压失去稳定。

3)由负载一侧造成的瞬变电压不稳定，在瞬态过程中，负载和控制设备都希望能够恢复负载的能量，而异步电机负载对瞬时电压的稳定起着重要的作用。当负载端电压下降时、当滑差超过不稳定平衡时、当发生故障时，负载将无法再次加速[14]。这些异步电机往往会产生堵塞现象，并会吸收大量的无功功率，造成邻近的母线电压下降，引起附近异步电机的闭锁，造成局部异步电机的无功要求猛增，区域电网的无功不平衡进一步恶化，形成正反馈的电压下降，最后造成系统的暂态电压不稳定。

从上述分析可以看出，影响暂态电压稳定性的主要因素有输电线路有功、无功、母线电压、直流线的传送功率等与工作状况有关的参数，如故障的部位、切割时间等。所以，在建立输入特征集时，要充分考虑到这些对暂态电压稳定性有重要影响的因素，使之能适应不同工况、不同类型的变化，从而构造出1种合理的特征值。为反映区域整体的稳态运行状况[15]，系统级的稳态特征构建如下：

1)特征量 1、2：稳态时发电机的有功出力、无功出力之和为

(9)

(10)

式中，n为发电机总数，Qi、Pi分别为发电机的有功功率与无功功率。

这2个特征量反映了稳态时区域发电机有功功率、无功功率总水平。

2)稳态时风机的有功功率、无功功率之和为

(11)

式中，n为风机总数，Pi、Qi分别为稳态时有功功率和无功功率。

在受到干扰后，所选择的电压稳定评价点的电位距离愈接近，瞬时电压反应愈接近，稳态特性对评价点暂态电压稳定性的影响愈大，其所含的有效信息愈多。因此，选择各分区评价点和邻近地区的稳定单元水平特性，作为1个输入特征量。

3 直流配电网惯性分析

在上述基本方程的基础上，对直流配电网的惯性进行分析，公式表示为

(12)

式中，Ek为转子在额定速度下所储存的动能，SN为发电机额定功率，J为转子的惯性矩，ω为转子机械的转速。

直流系统和 AC的惯性定义一样，都可以反映出一个系统的电压突然变化，公式为

(13)

式中，Ci为并联电容值，Si为第i个电容的容量值，U为直流侧并联电容的数目。

随着电容器容量的增大，额定电压储存更多的电能，其惯性常数和系统的惯性也会增大。

接着，对虚拟惯性进行分析，给出电压和电流的表达式：

(14)

式中，Io、Ii分别为直流侧方向的电流和交流侧朝向 测量电容的电流，C为直流侧电容值，Udc为有功功率。

在上述惯性分析基础上，选择薄弱节点，在节点静电压不稳定的概率指数即将达到临界值时，避免单字成行须采用相应的控制措施来减小该概率指数，并将其比作

pi>kplim，

(15)

式中plim为预设的关键指数。

为便于计算，采用以下公式对薄弱节点进行标准化处理：

ci=pi/pmax(i=1,2,…,L)，

(16)

式中，L为弱节点总数，pmax为电压不稳定的概率指数在全部负载节点中的最大值。

在选取薄弱节点后，增加节点的振幅可以改善系统的静态电压稳定，因此，要减少节点的静态电压不稳定，就必须增加薄弱节点的电压振幅，相应的优化目标函数表示为

(17)

式中，Ω为所识别的1组弱节点，Ui为薄弱节点的电压幅值。

基于上述过程对直流配电网惯性进行特性分析，可以为后续电压稳定性控制提供基础。

4 虚拟惯性控制策略

4.1 受端电压稳定判据解析

在对传统负载母线电压稳定性进行分析的基础 上，提出1种适用于电力系统的直流电压稳定准则：

(18)

式中，dQfl为无功功率值，dPd、dU分别为直流系统输送有功功率和电压灵敏度值。

在实际工作中，总负载对静态电压有一定的影响，并将其表达为

△P=Pd-(-Pf)=0,

△Q=-Qeq-(-Qf)=0,

(19)

式中，Pd、Pf分别为交流端的有功和无功功率，Qf为补偿器补偿的无功功率。

考虑到节点负载的波动，由于负载的变动和分配功率的不稳定，系统的输出功率也会发生变化，而电压的改变速率越低，系统所需的功率也就越大。为达到以上要求，首先给出了一个分段的虚拟惯性控制方案：

(20)

式中，C0为稳定时的电容值，k为调整系数，m0、m1分别为电压变化率的阈值。

上述过程对受端电压稳定判据解析，并预先给出了一个分段的虚拟惯性控制方案。

4.2 模糊控制实现

通过对直流母线电压进行模糊预测控制，使直流侧的电压由三相整流后，达到预定的直流母线电压，从而实现了对负载电流瞬态的稳定控制，有效地抑制了电压过调、电流涌流等现象。

模糊规则是经验和实际应用的结果，其数学模型准确，且控制规律简单、经验化。利用对闭环控制系统的阶跃响应的时间域方法，对直流母线电压的稳定性进行研究，给出一种基于自调整因子的模糊预测控制方法。自调整因子可在全控制区根据瞬时负荷状况，自动调整控制策略，采用抛物线外插法，实现对直流母线电压的最优控制。

自适应模糊控制规则表示为

(21)

式中，α、αs分别为自调节因数，N为划分的 区间数，△u、e*分别为模糊控制器的输入变量。

基于上述理论，建立模糊控制器结构见图2。

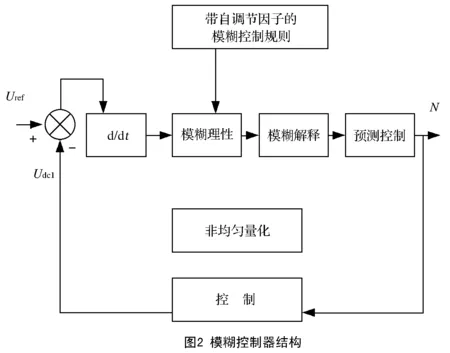
基于上图可得

e=[(Uref-Udc1)-(Uref-Udc2)]△t,

(22)

其中，t为采样的时间，Udc1、Udc2分别为离散化处理参数。

不断迭代上述过程，实现直流电网暂态电压稳定性自动控制。

5 实验

为验证所提出的考虑节点负荷波动的直流电网暂态电压稳定性自动控制方法的控制效果，进行实验，并将柔性直流电网的暂态稳定判据与电压恢复控制技术、直流电网暂态过电压机理与抑制策略与 所提出的方法对比，对比3个方法对电压的控制效果。

预先对比无干扰下控制效果，对比结果如图3和图4所示：

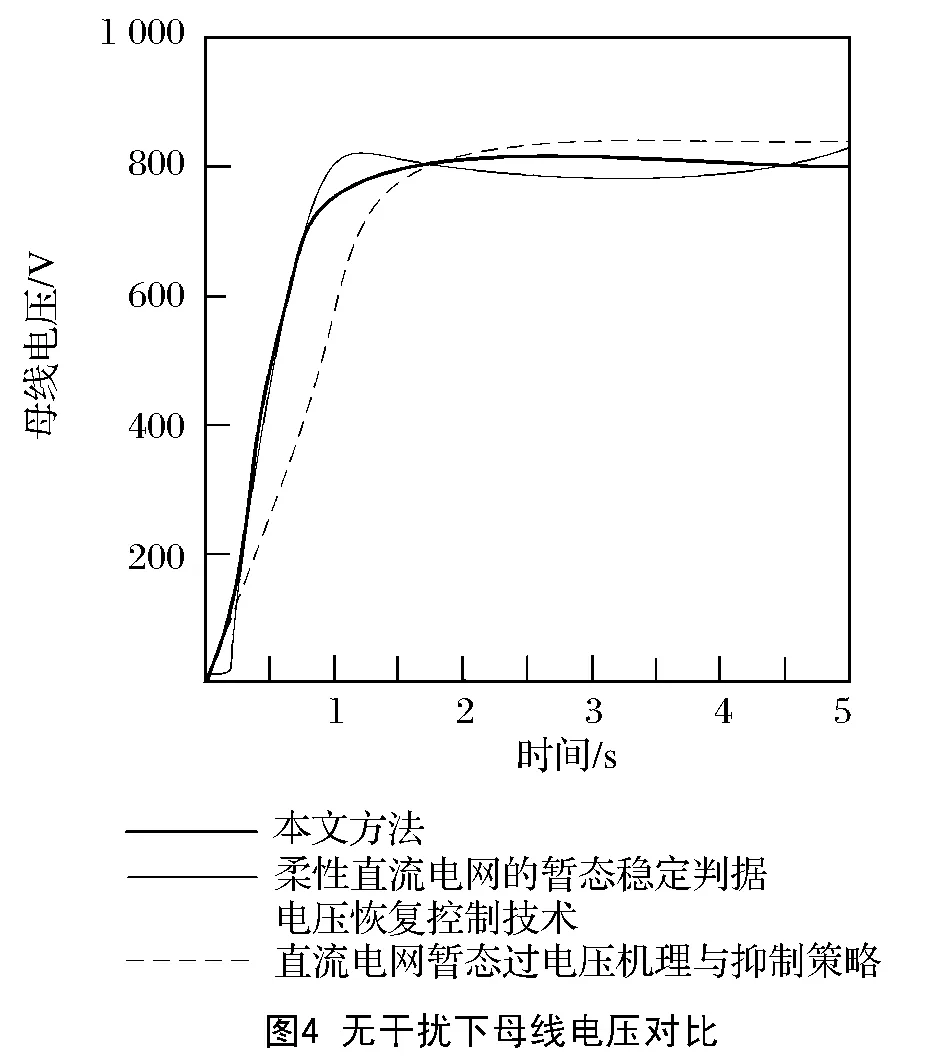
从图3和图4可知，在没有干扰的情况下，3个方法对电网电流控制与母线电压控制效果都较好，波动较小，但经对比能够发现，本文所提出的方法仍比另2种方法控制效果好。

接下来对比有干扰情况，加入故障节点后3个方法的控制效果对比结果如图5和图6所示。

从图5和图6可知，在有干扰情况下，本文提出的方法可以很好地抑制和改善噪声，但是其他2种方法都存在很大的干扰，而且电流和电压的变化也很大，说明另外2种方法的控制效果不如本文所述方法。