XK715型数控机床主轴箱谐响应仿真分析

张 旭，戴晓东，徐光晨，李玉爽，贾贤安

(1.芜湖职业技术学院 智能制造学院，安徽 芜湖 241006；2.合肥工大共达工程检测试验有限公司，安徽 合肥 230009)

机械装备中，精密零件的制造工艺对数控设备精度要求高，排除数控机床自身加工精度等级因素，数控加工质量还受环境温度、机械振动、伺服参数设置等一系列因素的影响。数控加工过程中，产品表面振纹一直是影响加工质量的“拦路虎”，数控设备的受迫振动响应规律与振纹的产生有直接联系。数控机床在正常工况下，机床硬件系统所受外界激励模型多为简谐函数，因此，可以通过有限元谐响应分析(finite element harmonic response analysis)的方法研究稳态简谐载荷作用下的数控机床受迫振动规律，分析影响振纹产生的关键因素，从而指导数控加工生产实践，对产品质量控制具有重要意义。

1 谐响应分析数学模型的建立

模态分析是利用模态叠加法进行谐响应分析的基础，分析的基本思路是在ANSYS Workbench环境中先建立主轴箱的自由模态分析项目并求解模态，然后将自由模态项目中的相关参数，如数字化模型、工程材料设置、网格处理结果、后处理数据等导入谐响应分析项目中，在此基础上添加谐响应分析所需的固定约束、特定振型频率等边界条件，从而计算主轴箱的谐响应规律。

1.1 模态分析数学模型

对主轴箱模态分析时，主要是将其线性定常系统振动微分方程组中的物理坐标转换为模态坐标使其方程解耦。基于机床实际工况建立主轴箱有阻尼交迫振动时的振动微分方程[1]：

(1)

在主轴箱的振型分析时，因主轴箱所受系统各 方面的阻尼可以忽略，且外载荷为零，即c=0，F(t)=0，因此可将公式(1)转化为系统无阻尼的自由振动方程：

(2)

主轴箱的自由振动为简谐振动，即位移为时间的正弦函数，且初始相位角为0，则有

X(t)=Φsin(ωt)，

(3)

式中ω、Φ分别是系统自由振动时的固有频率和对应的振型。

将公式(3)带入(2)可以解得广义的无阻尼振动特征方程：

KΦ=ω2MΦ。

(4)

方程(4)有非零解的条件是

|K-ω2M|=0。

(5)

由公式(5)可知，对于自由振动系统求解的实质，即是求解特征值ω2和特征向量Φi，而ωi、Φi分别是系统自由振动时的固有频率和对应的振型。

1.2 谐响应分析数学模型

机床主轴箱谐响应分析的目的是确定在特定激励载荷频率下主轴箱受迫振动的响应值(如位移等)对频率的曲线，从而使设计人员能够预测机床结构的动力特性，验证设计是否能够克服共振、疲劳以及其他受迫振动引起的不利影响。根据自由度系统的特点，确定主轴箱的动力学方程为[2]

(6)

谐响应分析时，输入的圆频率都为Ω，可以求解出谐响应分析的运动方程为[3]

(-ω2M+iωC+K){x1+ix2}={F1+iF2},

(7)

式中：ω是激振频率；{x1+ix2}是节点位移矩阵(复数形式)；{F1+iF2}是系统所受载荷(复数形式)。

实际谐响应分析时，在ANSYS Workbench软件中施加的谐波载荷为多个载荷，相位角默认为零,为了仿真分析时简单高效，可根据模态分析结果，取合适的激振频率区间用以研究谐响应规律。

2 主轴箱模态分析及谐响应分析

在有限元仿真分析软件ANSYS Workbench环境中建立整体分析项目，通过主轴箱三维模型项目A的建立、模态分析项目B的建立以及谐响应分析项目C的建立，并关联3个分析项目，实现不同项目间的数据共享[4]。主轴箱的谐响应分析项目逻辑如图1所示。

2.1 主轴箱模态分析

模态分析时，需在仿真环境中添加主轴箱数字模型的工程材料属性，此处选用灰铸铁(gray cast iron)材质，其密度为7.2×10-6kg/mm3，杨氏模量为1.1×105MPa，泊松比为0.28。综合考虑模态分析的准确度和运算速度，控制主轴箱网格划分的尺寸为10 mm，跨度中心角为中等，得到主轴箱的网格划分参数设置及结果如表1所示。

表1 主轴箱网格划分情况

主轴箱网格划分后的整体效果如图2所示。

因XK715数控机床主轴箱与Z轴导轨间采用塞铁进行连接预紧，且Z轴滚珠丝杠副的螺母与主轴箱的紧固方式为平面连接[5]，故设置主轴箱的固定约束条件为导轨燕尾槽处的5个接触面，如图3所示。

经上述分析设置，求解得出主轴箱的前6阶模态振型如表2所示。

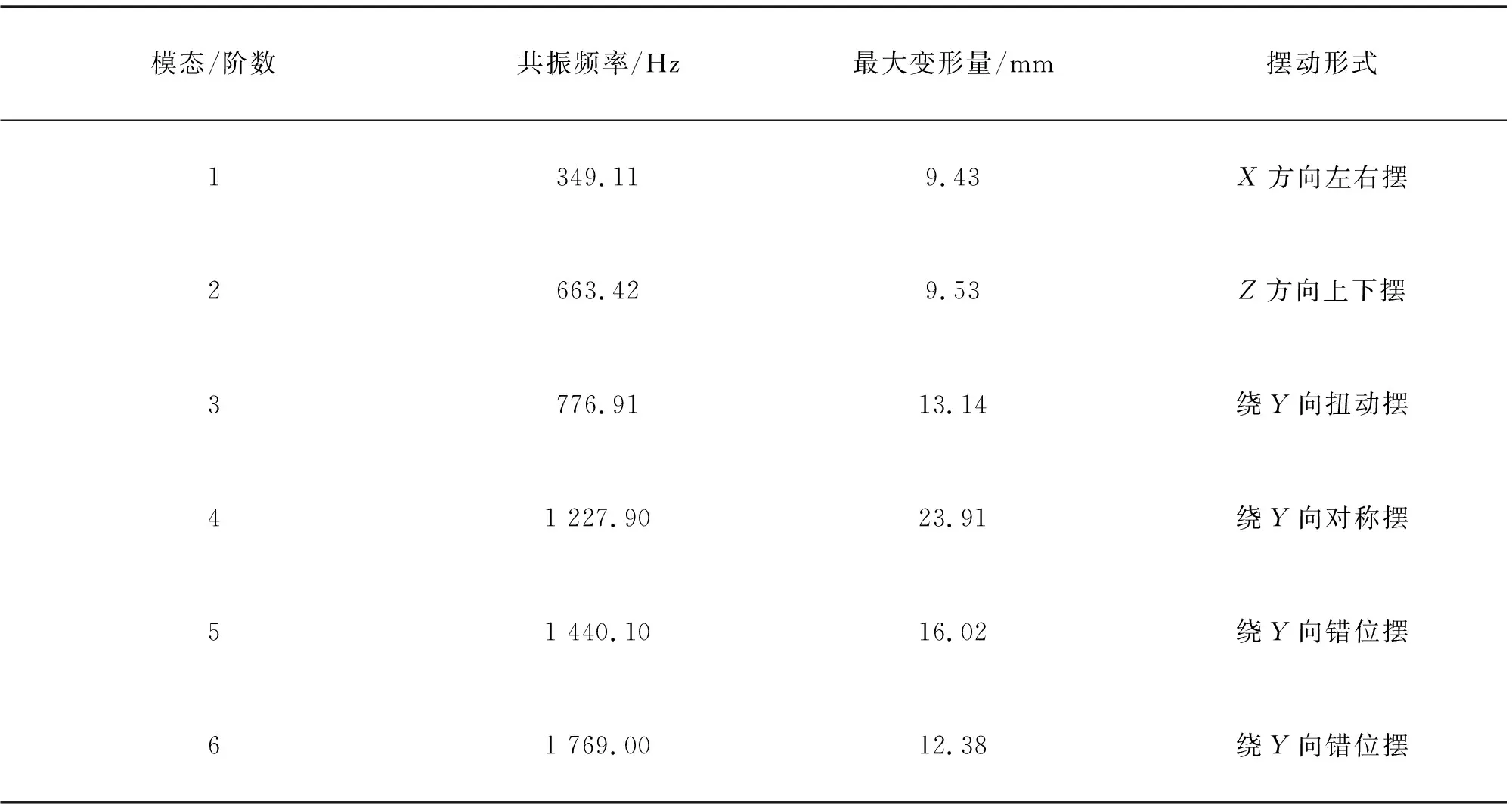
表2 主轴箱前6阶模态振型

主轴箱前6阶模态变形云图如图4所示。

从图4中可以看出：主轴箱在4阶振型下的形变量最大，最大值为23.91 mm，位置在主轴箱体上沿阶梯转角处；主轴箱在1阶振型下的形变量最小，最小值为9.43 mm，位置在主轴箱上边缘外侧两尖角处。

2.2 主轴箱简谐载荷分析计算

在谐响应分析中，除重力载荷、热载荷、旋转速度、螺栓预紧载荷及压缩约束外，其他形式的机械载荷均可以施加[6-8]。因此，为进一步分析主轴箱谐响应规律，需通过计算确定主轴箱所受到的外界简谐载荷。外界的简谐载荷需要通过幅值、频率和相位角3个参数进行定义。ANSYS Workbench仿真分析中，相位角默认为零，因此，主要问题在于求得外界简谐载荷的幅值参数。

XK715数控机床在切削过程中主轴箱所受的简谐激励载荷主要源自3个方面：1)机器自身机械传动系统(如齿轮传动、带轮传动等)平稳运行时产生的循环载荷；2)主轴系统相关运动零部件的同轴度误差(如刀柄与主轴锥孔间的同轴度、刀柄与刀轴间的同轴度等)产生的循环载荷；3)机床在切削过程中，刀具和加工工件之间的切削力产生的循环载荷。当上述3种简谐激励叠加作用于主轴箱时，若形成的振动频率趋近于主轴箱的前6阶中某一固有频率时，主轴箱即发生共振现象。

数控机床投入运行前需经过严格的技术测试，并调修符合相关国家标准，机械传动系统的循环载荷和主轴系统同轴度误差均可控制在极小的范围[9]。因此，机床主轴箱所受的外界简谐载荷主要是加工过程中刀具和工件之间产生的切削力。

根据金属切削理论和铣削主切削力计算公式[10]，求解切削力Fc大小：

(8)

式中：fZ为切削加工时的进给速度(mm/min);B为铣削宽度(mm)；cp为工件材料对切削力影响系数；K为刀具前角对切削力的影响系数；K1为切削速度对切削力的影响系数；d0是铣削刀具直径(mm)。

有限元模拟分析时，尽可能大地选择相关参数，以便得到更加可靠的分析数据[11]。设定机床切削要素为：主轴转速n=600 r/min，进给速度f=200 mm/min，切削深度ap=5 mm；切削宽度ae=B=6 mm；所选刀具为双刃端铣刀，刀具直径为16 mm。

根据上述加工工艺参数，选择表3、表4、表5中对应的影响系数：cp=50，K=1.2，K1=1.0。

表3 工件材料对切削力影响系数

表4 刀具前角对切削力影响系数K

表5 切削速度对切削力影响系数K1

由公式(8)最终计算得到切削力的值为

Fc=714.89, N≈715 N。

铣削时不同方向切削力计算公式[12]：

Fc∶Fp∶Ff=1∶0.8∶0.6。

(9)

式中：Fc为X方向的切削力值；Fp为Y方向的切削力值；Ff为Z方向的切削力值。

由此，可计算其他2个方向的切削力值为

Fp=572 N,Ff=429 N。

切削力通过刀具、刀柄、主轴锥孔传递到主轴箱上，在此过程中忽略切削力的传递介质(即刀具、刀柄、主轴锥孔)的形变，认为传递介质为绝对刚体[13]，因而可将上述计算所得切削力赋予主轴箱。

主轴箱所受外界简谐激励载荷等效为刀具的切削力载荷，因此，结合有限元分析设置要求，分别确定各方向受简谐载荷幅值为：Fc=FX=715 N；FY=Fγ=572 N；Ff=FZ=429 N。此结果中的X、Y、Z方向可参考图2中的坐标方向。

2.3 主轴箱谐响应仿真分析

利用模态叠加法分析谐响应问题的优势是计算量少，且能够考虑预应力的作用效果，能够将研究对象的动力学矩阵方程求解的结果收敛在前期模态分析所得出的固有频率附近[14]，对于简单结构的动力学分析实用性较强，简谐载荷幅值确定后，即可通过模态叠加法分析计算主轴箱的简谐响应。

因案例中设置的铣削刀具为端铣刀，其主要作用为加工平面，切削时主要使用端面的刀刃进行切削，加工质量评价倾向于零件的表面振纹，垂直于被加工表面的刀轴方向上的振动直接影响振纹的产生及严重程度，即沿主轴方向(XK715数控机床Z轴方向)的刀具振动对机械零件表面质量影响较大[15]，主轴与主轴箱通过主轴端面法兰固接于主轴箱体上，因此，将谐响应分析的输出位置设置在主轴箱体和主轴连接的端面法兰处。如图5所示。

设置谐响应分析的解决策略(solution method)为模态叠加法，根据前3阶模态振型的频率大小，设置响应频率(frequency response)区间为0～1 000 Hz，取100个频率节点，输出方向为Z方向，求解得到主轴箱端面及整体的谐响应分析结果，如图6～图9所示。

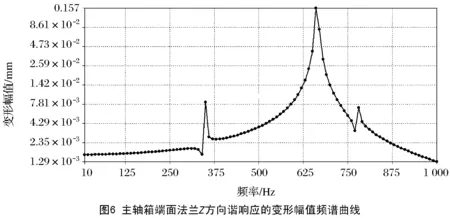
从图6中可以看出，主轴箱端面法兰Z向的变形输出值受外界简谐载荷影响较大，通过查看曲线中的节点，发现当激励载荷频率在350、660和780 Hz时，主轴箱端面法兰对应的变形量输出峰值分别为8.282、156.910、6.970 μm。分析数据频率和模态分析前3阶振型的固有频率349.11、663.42、776.91 Hz相吻合，证实了利用有限元法进行谐响应分析时的模态叠加法的正确性。

从图7中可以看出，端面应力幅值频谱曲线的变化规律和变形幅值频谱曲线的结果不存在明显关系，即当激励载荷频率在350、660、780 Hz时，端面Z方向的应力输出值会达到区间范围内的最大值，最大值分别为6 464.90、917.42、4670.30 Pa。最大应力值6 464.9 Pa相对于主轴箱采用的灰铸铁材料的杨氏模量1.1×1011Pa可忽略不计，主轴箱体的刚度能够满足加工需求。

从图8中可以看出，660 Hz频率下，主轴箱谐响应的等效应力最大应力值点处在主轴箱矩形框架下边缘的90°拐角处，其值为63.29 MPa，相较于主轴箱材质灰铸铁的抗拉强度250 MPa较小，对主轴箱的强度不构成威胁[16]。

从图9中的分析结果可以看出，660 Hz频率下，主轴箱变形量的最大值在主轴箱端面法兰前部，其值为0.22 mm，大于端面法兰Z方向谐响应的变形幅值频谱曲线中的谐响应输出最大值156.91 μm(≈0.157 mm)，这是在多种载荷共同叠加作用下的结果。在此频率作用下，主轴箱整体的摆动情况是上下振动，不利于机械产品加工质量控制，因而要避免主轴箱在此频率附近的简谐载荷作用下运行。

3 小结

1)基于谐响应分析基本原理，在ANSYS Workbench环境中建立了主轴箱的谐响应分析模型，并利用模态叠加法计算主轴箱的前6阶振型，得到主轴箱在1阶振型下的最小形变量为9.43 mm；主轴箱在4阶振型下上端面中部垂直转角处的形变量最大值为23.91 mm，后期进行结构优化设计时可考虑在此处布置加强筋、加强肋板，以提高此处结构的强度和刚度。

2)结合机床实际工况，分析计算了主轴箱所受简谐载荷参数，确定主轴箱在X、Y、Z坐标方向所受外界载荷幅值参数，即切削力大小为：Fc=FY=715 N；Fp=Fγ=572 N；Ff=FZ=429 N，为机床实际受载研究提供了参考方法。

3)分析主轴箱端面法兰在0～1 000 Hz的变形幅值频谱曲线和应力幅值频谱曲，并得到外界简谐载荷频率在660 Hz下主轴箱端面最大变形量为0.22 mm，为后期机床结构动力学分析试验提供了数值参考。