基于Actor-Critic学习的数控机床加工过程控制方法

黄 苏

(厦门海洋职业技术学院 海洋机电学院，福建 厦门 361102)

数控机床包含机床、刀具与工件等，其加工过程属于动态过程[1]，数控机床加工过程易受大量因素与参数影响，例如切削力与进给速度等，导致加工过程无法达到最优状态，直接影响数控机床加工效率与加工质量[2-4]。因此，需要对数控机床的加工过程进行控制。梁建智等依据数控机床加工过程运行特性，建立等价数据模型，通过数据驱动，设计控制方法，按照迭代轴动态线性算法，依据最小化控制目标函数，实现了控制增益的自适应修正，提升了控制方法的收敛速度[5]，但是该方法控制加工过程的平均绝对误差较大，影响数控机床加工效果。马丽等通过UG软件与VERICUT软件模拟加工过程，该方法可完成并有效控制加工过程[6]，但在控制数控机床加工过程中缺乏稳定性，降低数控机床的工作效率。

Actor-Critic学习同时具备近似值函数与策略函数的特性[7]，与PID控制器结合可有效提高机床加工的控制效果。因此，为解决上述方法的不足，本文基于Actor-Critic学习算法，设计了1种数控机床加工过程控制方法，可以有效控制数控机床加工过程，提升数控机床加工过程稳定性。

1 数控机床加工过程控制方法

1.1 数控机床加工过程模型

数控机床单轴给进系统的动力学方程[8]为

(1)

式中，Ml为数控机床工作台质量，Xt为数控机床工作台轴向位移，l为滚珠丝杠导程，Xl为滚珠丝杠的轴向位移，C1为导轨阻尼系数,Ke为电机等效转动惯量。

基于动力学特性，针对数控机床动态特性[9]，系统的动力学方程为

mx+(c+cj)x+(k+kj)x=0,

(2)

式中，m为数控机床质量矩阵，c与cj为机床和结合部阻尼的矩阵，k与kj为机床和结合部刚度的矩阵，x为数控机床主轴。

结合数控机床有限元分析模型，数控机床加工效率传递函数为[10]

(3)

式中，a为传递导程，m与n为常数，s为伺服增益，T为增益时间。

设Fo表示切向力，Fw表示径向力，Fe表示轴向力，数控机床动态切削力方程为

(4)

式中，u为切削刃接触边长度，Kic(i=o,w,e)与Kib(i=o,w,e)为动态切削系数，h(α)表示瞬态切削厚度。

1.2 基于Actor-Critic学习的自适应PID控制

Actor-Critic学习采用模糊推理系统(fuzzy inference system，FIS)与径向基函数神经网络(radial basis function，RBF)相结合的网络结构，即基于FRBF的模糊Actor-Critic学习结构，结合自适应PID控制器，设计基于Actor-Critic学习的自适应PID控制方法，控制数控机床加工过程。具体步骤如下：

步骤1：初始化PID控制器的参数；

步骤3：将xt作为基于FRBF的模糊Actor-Critic学习网络的输入向量，通过FRBF的模糊Actor-Critic学习网络，初步优化PID控制器，将其应用于数控机床加工过程模型中；

步骤4：预测数控机床加工过程模型下一采样时间的输出函数与回报函数，求解值函数与TD误差，通过结构学习与参数学习，优化FRBF的模糊Actor-Critic学习网络，获取最佳的FRBF的模糊Actor-Critic学习网络结构；

步骤5：在最佳FRBF的模糊Actor-Critic学习网络内输入xt，输出PID控制器最佳参数，得到自适应PID控制器，将其应用到数控机床加工过程模型中，实现对数控机床加工过程的控制。

1.2.1 基于PID控制器的加工过程控制

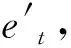
(5)

式中，Ft为PID控制器输出的数控机床加工过程切削力测量值，t为时间，Tj、Td为积分与微分的时间常数。

PID控制器的增量式算法为

(6)

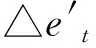
1.2.2 PID控制器参数优化

利用基于FRBF的模糊Actor-Critic学习网络，优化数控机床加工控制的PID控制器参数K， 建立自适应PID控制器，提升数控机床加工控制效果[12]。

将xt作为FRBF的模糊Actor-Critic学习网络的输入，输出最佳的K。FRBF的模糊Actor-Critic学习网络共包含4层，分别是输入层、规则层、归一化适应度计算层、输出层。

首层内各神经元均对应1个数控机床加工控制 的PID控制器的状态变量xα，均可直接传输至第2层。

第2层内各节点均对应1条优化数控机床加工控制的PID控制器参数的模糊规则[13]，均包含m个高斯型隶属度函数ραβ，公式如下：

(7)

式中:α∈m；h为规则节点数量，β∈h；η为模糊系数；μαβ、σαβ表示ραβ的中心与宽度。

第β条优化数控机床加工控制的PID控制器参数的模糊规则的适应度为

(8)

式中xαt为t时刻x的第α个分量。

第3层内节点数量与上1层节点数量一致[14]，负责归一化处理φβ，公式如下:

(9)

最后1层包含Actor与Critic 2个部分，利用Critic近似优化数控机床加工控制的PID控制器参数状态值函数，将xt映射成期望评价值S(xt)，即值函数，通过Actor生成优化数控机床加工控制的PID控制器参数的合理动作，将xt映射至动作空间，获取动作概率函数K′(xt)，即最佳的Actor数控机床加工控制的PID控制器参数分量K=[Kp,Kj,Kd]，网络输出的第k个动作的动作概率函数为

(10)

式中:wkβ为第3层与Actor网络的连接权值；γ1为常数，γ1>0。

Critic网络输出的S(xt)为

(11)

(12)

Actor和Critic都通过TD法学习S(xt)与K″(xt)，通过状态转移时邻近S(xt)的时间差分求解TD误差δTD，公式如下:

δTD=rt+JτS(xt+1)-S(xt)，

(13)

式中:rt为优化数控机床加工工程PID控制器参数的回报信号；折扣系数是τ的取值区间为(0，1)；J表示学习性能指标。

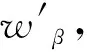
(14)

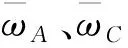
通过结构学习优化网络第2层与第3层的节点数量，提升网络泛化效果，加快收敛效率。通过增加节点完成结构学习，即由增加节点，扩展的覆盖度，获取标准TD误差，输出更佳的A(xt)。

令Φβ为基函数，qβ为平均局部加权TD误差，yβ为平方TD误差，利用Φβ的局部误差求解标准TD误差，移动Φβ的qβ与yβ，获取网络节点局部误差，公式如下：

qβ(t+1)=qβ(t)-τΦβ(qβ(t)+φβδTD),

(15)

(16)

(17)

FRBF的模糊Actor-Critic学习网络完成结构学习与参数学习后，在该网络内输入优化PID控制器的K，得到最佳数控机床加工过程PID控制器的参数，获取自适应PID控制器，通过自适应PID控制器完成数控机床加工过程控制。

2 实验分析

为验证本文提出的基于Actor-Critic学习的数控机床加工过程控制方法的有效性，选择某加工中心的XH825D数控机床作为实验对象，利用本文方法控制该数控机床的加工过程，该数控机床的基础数据如表1所示。

表1 数控机床基础数据

数控机床加工材料选择PLA与30钢材料，设精车进给量为0.1～0.3 mm/r，选择直径6 mm铣刀，转速为3 000 m/min。分析本文方法在该数控机床加工不同材料时的加工过程控制效果，加工这2种材料时数控机床的走刀均是15 mm×45 mm，数控机床加工过程控制效果如图1所示。

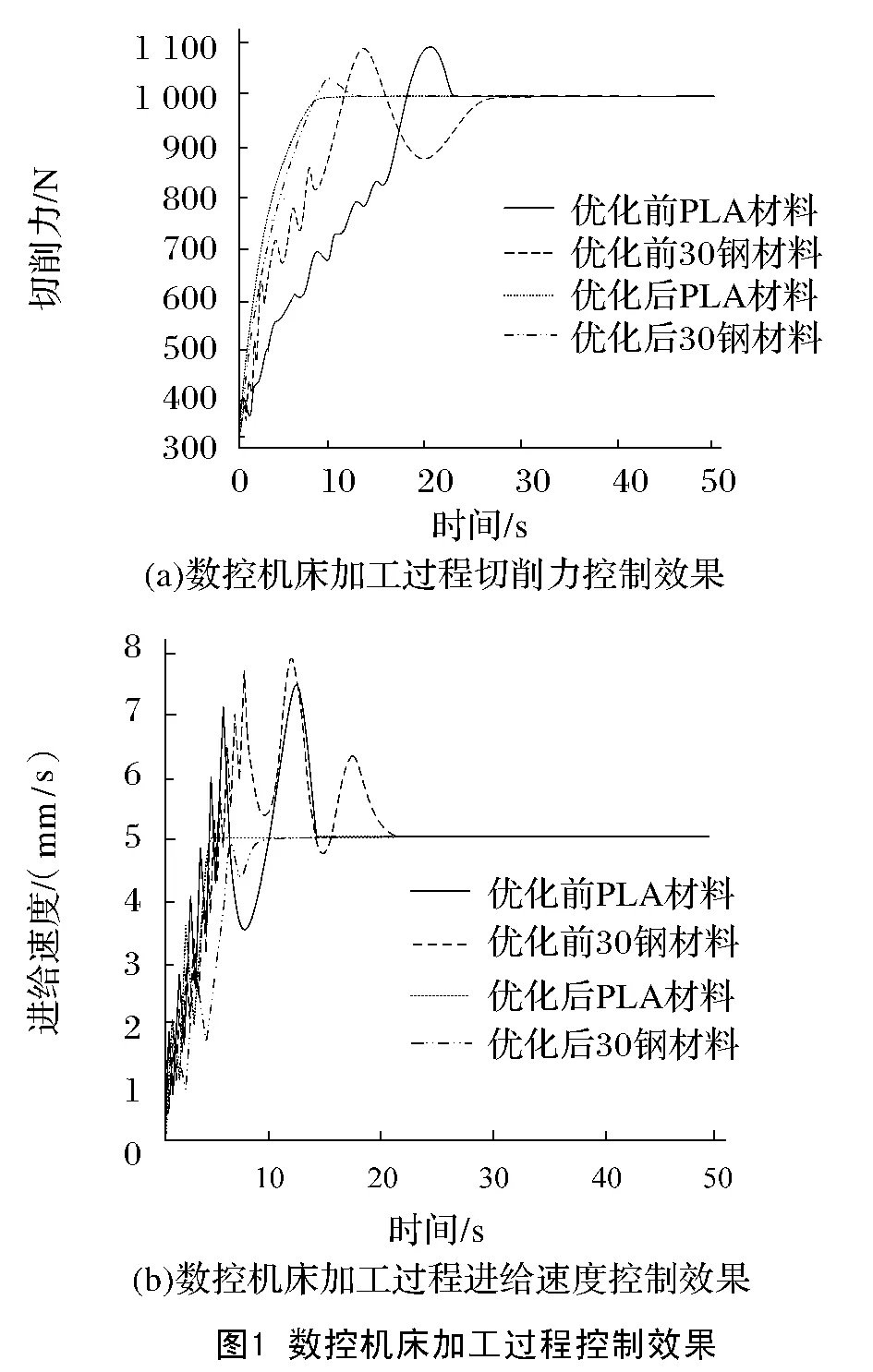
根据图1可知，本文方法可有效控制数控机床加工过程的切削力与进给速度，优化PID控制器后，2种材料加工过程的切削力与进给速度控制效果明显优于优化PID控制前；优化PID控制器前后，PLA材料加工过程切削力与进给速度完成控制的时间均短于30钢材料；优化PID控制器前，2种材料加工过程切削力较高，进给速度较大，出现过冲现象，而优化PID控制器后，PLA材料加工过程切削力与进给速度控制时均无过冲现象发生，30钢材料加工过程切削力与进给速度控制时的最大偏差较小。实验证明，在加工不同材料时，本文方法均可有效控制数控机床加工过程，在优化PID控制器后，具有较好的控制效果。

利用跟踪误差平方ISE衡量本文方法控制数控机床加工过程的精度，ISE值越小，说明数控机床加工过程控制精度越高，最大ISE值为5，利用绝对误差积分ITAE衡量本文方法控制数控机床的平稳度，ITAE值越小，说明数控机床加工过程控制平稳度越佳，最大ITAE值为0.8。本文测试ISE与ITAE的不同切削深度测试结果如图2所示。

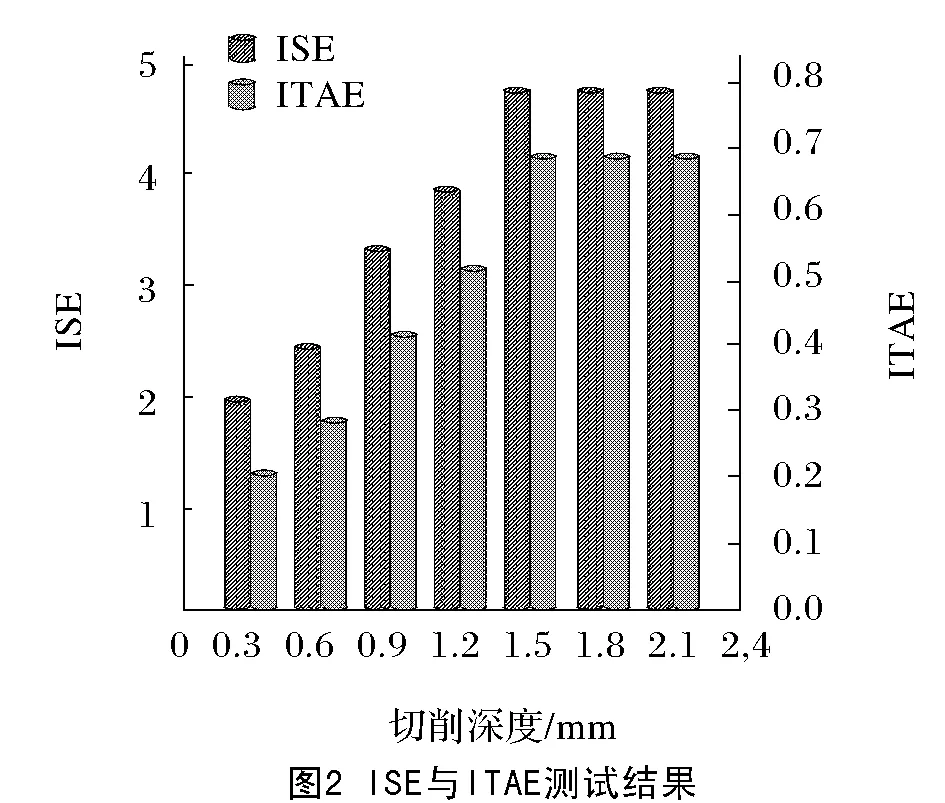
根据图2可知，随着30钢材料切削深度的增加，本文方法控制数控机床加工过程的ISE值与ITAE值均呈上升趋势，当切削深度达到1.5 mm时，ISE值与ITAE值均趋于稳定，最高ISE值为4.8，最高ITAE值为0.7，均未超过最大值。实验证明：30钢材料在不同切削深度时，本文方法控制数控机床加工过程的ISE值与ITAE值均较低，说明应用本文方法对数控机床加工过程控制的精度较高，平稳度较好。

通过数控机床加工效率衡量本文方法的应用效果，分析应用本文方法前后，在不同切削负载率与实载率时的数控机床效率，分析结果如图3所示。

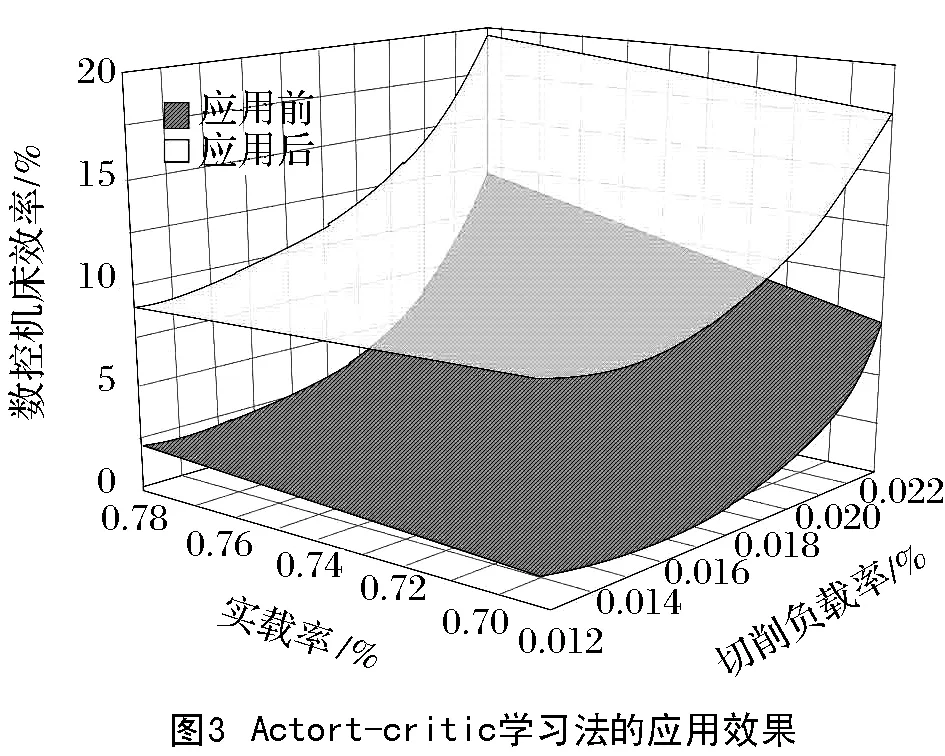
根据图3可知:应用本文方法前后，切削负载率与实载率越大，数控机床效率均越大；在不同切削负载率与实载率时，应用本文方法后的数控机床效率明显高于应用本文方法前。实验证明，采用本文方法，可有效提升数控机床效率。

3 结论

为解决传统控制方法在数控机床加工过程控制中存在控制精度较低的问题，本文提出基于Actor-Critic学习的数控机床加工过程控制方法，利用Actor-Critic算法优化PID控制器，利用切削力设定值和实际输出切削力测量值之差，获取PID控制器误差信号，输出最优补偿参数，通过自适应PID控制器调整进给速度来控制数控机床切削力，实现对数控机床加工过程的高精度控制。