基于负荷特性指标修正的地区能源经济循环模型研究

王东升， 陈重韬

(1. 国网冀北电力有限公司， 北京 100053； 2. 国网冀北电力有限公司 信息通信分公司， 北京 100053)

0 引言

能源消费是经济发展的催化剂，经济发展和能源消费具有较为显著的关联性，为了实现地区能源与经济的循环发展，需要深入分析能源与经济间的关系，实现两者均衡发展[1-3]。目前国内外很多相关研究人员使用多种方法对我国能源消费与经济增长的关系进行了针对性研究，但研究大多以定性研究为主[4]。本文从创新的角度，将能源消费作为负荷特性指标，构建一种基于负荷特性指标修正的地区能源经济循环模型。

1 地区能源经济循环模型

1.1 相关性分析

使用超越对数生产函数模型分析能源消费和经济增长的相关性，以此可分析能源消费对经济增长的贡献率[5]。生产函数模型为式(1)：

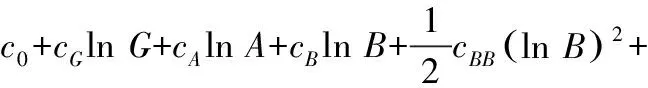
cGBlnG·lnB+cABlnA·lnB

(1)

式中，X、G分别表示当前经济系统的产出与资本存量，A、B分别表示当前经济系统中劳动力负荷特性指标投入量与能源负荷特性指标投入量，c0、cG、cA、cB、cGA、cGB、cAB均表示待定模型参数[6]。

资本、劳动力、能源的产出弹性公式为式(2)-式(4)：

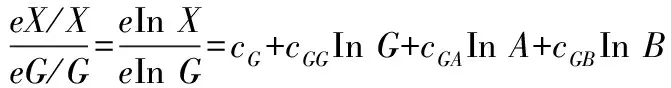
(2)

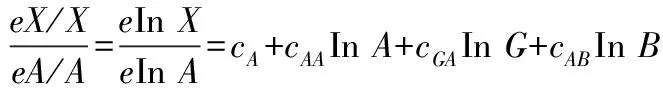
(3)

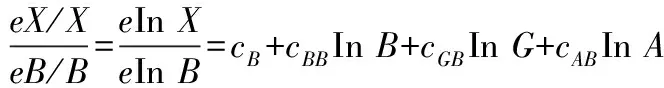
(4)

式中，ϑG、ϑB、ϑA依次表示资本、能源消费、劳动力的产出弹性，e表示弹性系数。根据式(5)计算“索罗余值”：

(5)

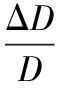
计算上述几种负荷特性指标对经济增长的贡献率为式(6)-式(8)：

(6)

(7)

(8)

其中，ξG、ξA、ξB分别表示资本、劳动力、能源消费3类负荷特性指标对经济增长的贡献率。

上述分析中，求解每个负荷特性指标对经济增长贡献率时的核心为求解超越对数生产函数里每个模型参数，运算获取每个负荷特性指标的产出弹性。求解方法使用岭回归方法[7]。

岭回归方法将多元线性回归方程设成式(9)：

P=Qλ·ψ

(9)

其中，P、Q分别表示因变量矩阵与自变量矩阵；λ、ψ依次表示回归系数矩阵与残差矩阵。残差矩阵的常规最小二乘估计为式(10)：

(10)

若自变量间相关性较为显著，自变量间相关系数矩阵值Q′≈0，此类情况下使用式(10)求解模型参数，会存在一定误差[8]。为此，在Q′≈0情况下导入一种正常数矩阵K，以此降低自变量间多重共线性的负面干扰。

这时的参数最小二乘估计为式(11)：

(11)

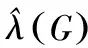
通过式(11)的回归系数估计值计算结果，完成能源消耗与经济增加相关性的分析。

1.2 能源经济循环发展优化模型

1.2.1 负荷特征指标的单位根检验

在相关单位根检验里，负荷特性指标数据生成为式(12)、式(13)：

xt=et+vt

(12)

vt=bvt-1+ut

(13)

式中，et、vt分别表示负荷特性指标确定性成分与随机项，ut是1阶单整(单位根)过程或0阶单整(平稳)过程中负荷特性指标单整项，则xt是差分平稳过程中负荷特性指标差分项，b为常数，t为时间参数。

在实证分析里，若序列里具有高阶状态，使用PP检验[9-10]检验方法是：

(14)

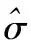
1.2.2 协整检验

协整检验包含基于回归残差的协整检验、基于回归系数的协整残差以及基于误差修正模型与格兰杰因果关系检验、H-P滤波。具体过程如下。

(1) 基于回归残差的协整检验

针对s个R1时间序列而言，存在qt种负荷特性指标x1 t,x2 t,…,xqt，能够构建3种负荷特性指标协整回归模型，如式(15)-式(17)所示:

(15)

(16)

(17)

式中，若vt属于单整变量，那么x1 t,x2 t,…,xqt不具有协整关系，反之x1 t,x2 t,…,xqt具有协整关系。

(2) 基于回归系数的协整残差

因为基于回归残差的协整检验对小样本参数估计时精度不高，所以本文通过Johansen检验方法，使用式(18)计算负荷特性指标的特征值，获取负荷特性指标协整向量，

(18)

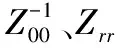
(3) 误差修正模型与格兰杰因果关系检验

使用格兰杰因果关系在误差修正模型框架中检验序列间修正效果。则有式(19)、式(20)：

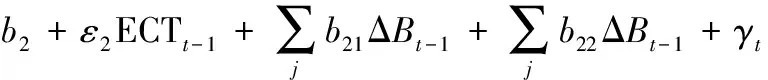
(19)

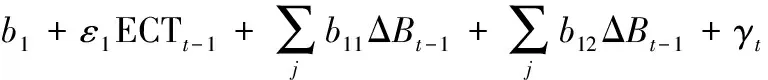
(20)

式中，ECTt-1是误差修正项，ΔBt-1是t-1时间段中能源消费量，ε1、ε2是平稳性检验因子，bn为常数。

(4) H-P滤波

针对xt使用H-P滤波方法时，需要符合式(21)给出的趋势条件：

(21)

式中，x、Hx分别表示观测变量与趋势成分。

通过H-P滤波后获取的周期成分为式(22)：

Dx=xt-Hx

(22)

将能源消费与经济增长实施H-P滤波分解，主要是为了获取能源消费和经济增长序列的趋势成分与周期成分，分析趋势成分与周期成分中趋势项与周期项的变化情况是否一致，以此确保误差修正的准确性。

2 实验分析

实验选取的数据为某市2010-2019年的经济增长值和能源消费总量数据，详情如表1所示。

将经济增长量与能源消费量分别简化为GDP、FC，单位分别是亿元与万吨。将本文实验使用的GDP与FC数据实施自然对数操作，设成OGDP、OFC。使用本文模型后，单位根检验结果如表2所示。

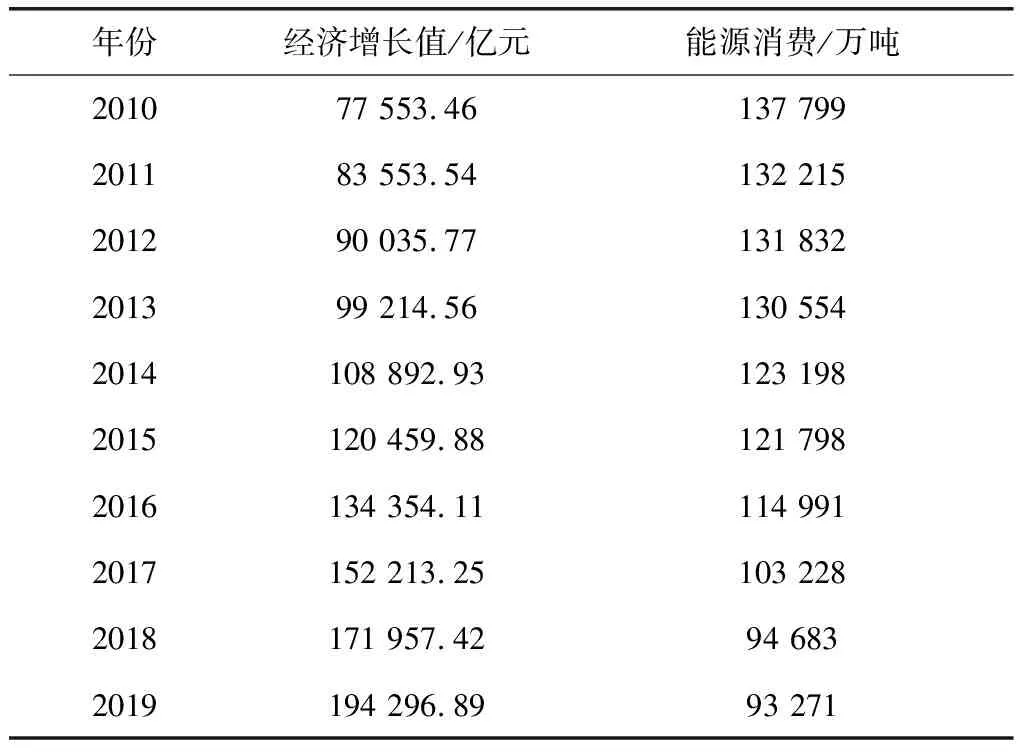
表1 实验数据

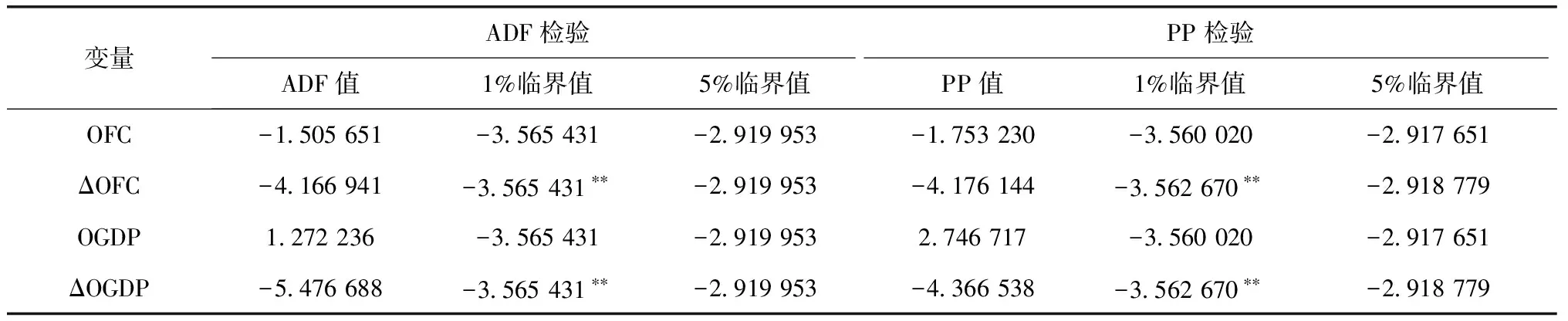
表2 单位根检验结果

表2中结果显示，不管是ADF单位根检验或者PP单位根检验，都表示OFC与OGDP在1%的显著程度中具有单位根，所以，能够将能源消费与经济增长间的关系实施Johansen协整检验。Johansen协整检验结果如表3所示。

协整方程是：OFC=0.596×OGDP+5.813。

按照协整理论，如果负荷特性指标具有协整关系，则使用该模型研究能源消费和经济增长间格兰杰因果关系、H-P滤波方法检验本文模型的修正效果，结果如表4所示。

分析表4中数据可知，短时间中能源消费的增长将催化经济增长，但经济在短时间中快速增长，并不会刺激能源消费的增多。但能源消费与ECT的F-统计量具有显著性，表示修正能源消费负荷特性指标存在可修正误差。联合检验表明，本文给出的模型修正能源消费和经济增长间误差后，能源消费和经济增长间0.01的临界水平显著，具有双向强格兰杰因果关系，两者均衡可实现地区能源经济循环发展。

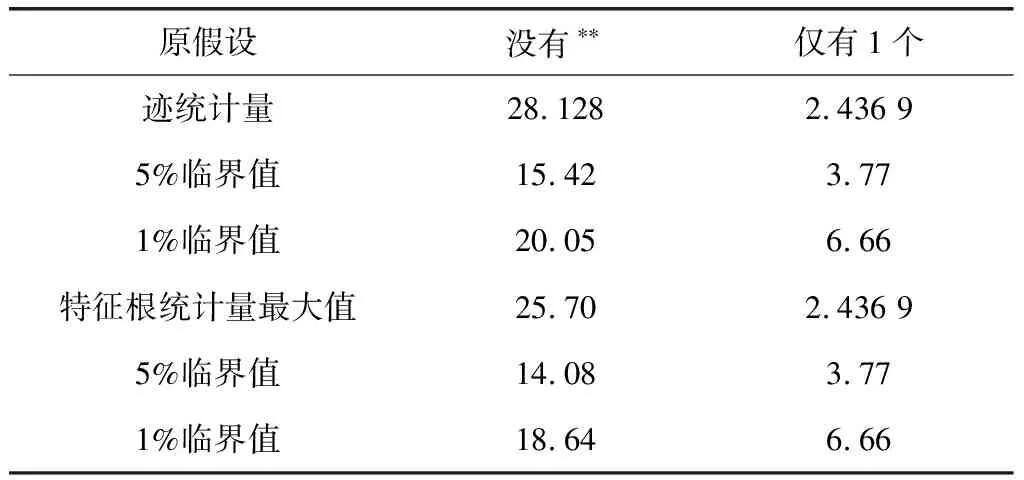
表3 Johansen协整检验结果

表4 能源消费和经济增长期格兰杰因果关系

为了验证本文模型修正效果，通过H-P滤波方法将OFC与OGDP进行分离，提取两者趋势项与周期项，两者趋势项设成HPOFC、HPOGDP，两者周期项设成ZFC、ZGDP。

提取结果如图1、图2所示。

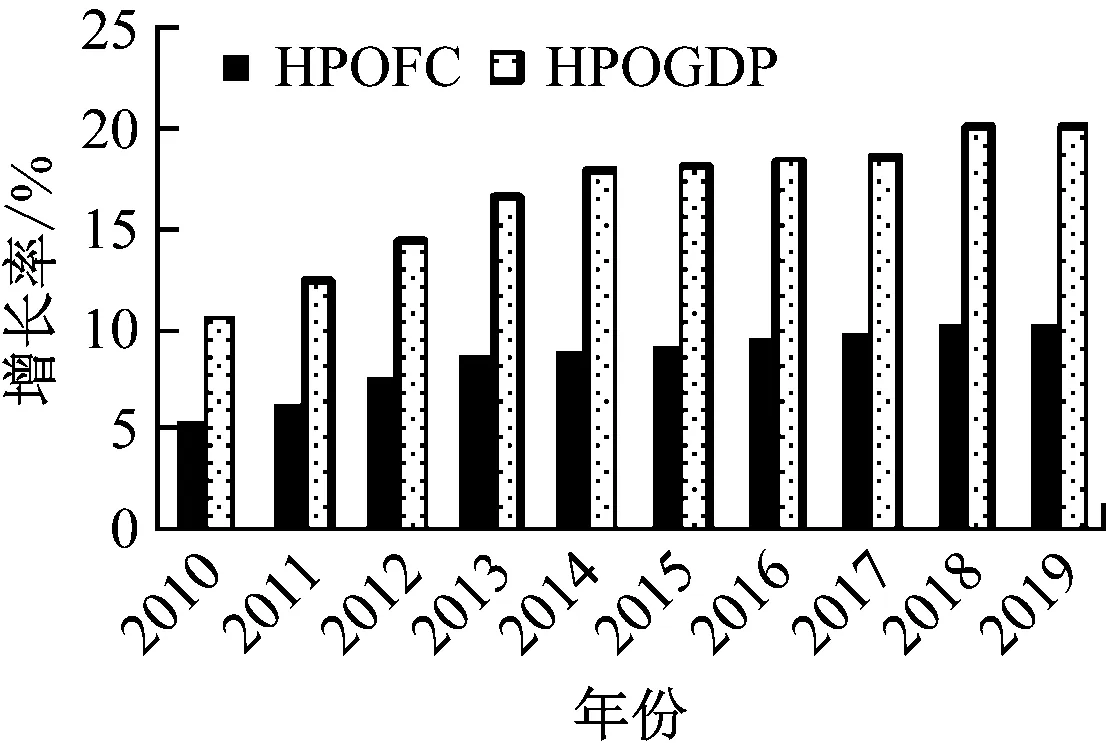
图1 OFC与OGDP经H-P滤波后的趋势项

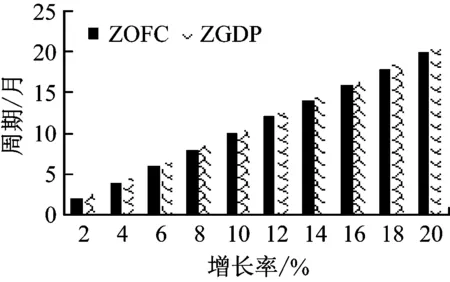
图2 OFC与OGDP经H-P滤波后的周期项

分析图1与图2可知，OFC与OGDP经H-P滤波后的趋势项与周期项变化情况显示，在本文模型修正下，能源消费与经济增长的趋势成分与周期成分变动状态极为相似，表示两者在本文模型的修正下，具有一致的发展趋势与相同变动特性，本文模型修正结果有效。

3 总结

能源属于我国社会发展中必需的物质基础，本文构建一种基于负荷特性指标修正的地区能源经济循环模型。研究结果显示，本文模型修正能源消费和经济增长间误差后，能源消费和经济增长间具有双向强格兰杰因果关系，两者均衡可实现地区能源经济循环发展；在本文模型修正下，能源消费与经济增长具有一致的发展趋势与相同变动特性，本文模型修正结果有效。