基于因子分解机用于安全探索的Q表初始化方法

曾柏森，钟 勇，牛宪华

（1.中国科学院成都计算机应用研究所，成都 610041；2.中国科学院大学，北京 100049；3.成都工业学院网络与通信工程学院，成都 611730；4.通信抗干扰技术国家级重点实验室（电子科技大学），成都 611731；5.西华大学计算机与软件工程学院，成都 610039）

0 引言

强化学习［1］是一种交互式机器学习方法，通过在环境中探索和试错来学习获取最大价值的最优策略，其中智能体的动作选择称为探索/利用策略。强化学习的大多数探索/利用策略都具有随机选择成分，这些方法不考虑随机动作选择的风险。然而，当强化学习应用于真实高风险环境时，在保证合理的系统性能同时确保智能体的探索不会造成损害或伤害尤其重要。因此，强化学习探索的安全性是亟须解决的问题［2］。

Smart 等［3］提出了一种利用示例和训练作为先验知识，引导智能体减少随机探索的时间从而更有效地学习的方法。Maire 等［4］提出了一种从人类现有演示中导出高质量初始Q表的方法。Song 等［5］利用领域知识初始化Q 值改进了Qlearning 算法性能，该算法可有效减少智能体移动到障碍物中的时间。Turchetta 等［6］提出了一种基于模型的强化学习探索方法，该方法能够在不违反先验未知安全约束的前提下安全探索决策空间。段建民等［7］利用环境的势能值作为启发信息对Q 表进行初始化，从而在学习初期便能引导移动机器人快速收敛。

为了提高Q-learning 的探索安全性，本文提出了一种基于因子分解机（Factorization Machine，FM）的Q 表初始化方法。该方法引入已探索经验Q 值作为先验知识，通过FM 建立先验知识中状态与行动的交互作用模型，从而预测未知Q值，进一步引导智能体与环境交互。实验结果表明，本文方法提高了传统探索/利用策略在Q-learning 中的探索安全性，同时也加快了收敛。

1 相关基础

1.1 探索安全性

强化学习的探索安全性没有统一的定义［8］，目前主要有三种定义探索安全性的方式：

1）通过标签定义安全。通过不同安全级别来标记状态/行动，例如：安全、负面、临界、致命［9］。这些标签的数量和名称因作者而异。

2）通过代价定义安全［10］。通过定义在状态下执行动作的代价，并将生成策略的最坏情况的成本降至最低。但是，并非所有不安全的状态都可以使用此类代价进行描述，此外设置正确的代价可能是一项艰巨的任务。

3）通过预期收益差异定义安全［10］。最小化损失和方差，是一种最小化代价（最坏情况或预期）的替代方案。根据这个标准的安全策略可以看作一个最小化不良动作数量的策略。

本文基于第3 种探索安全性定义，以期望减少Q-learning在探索过程中出现的不良动作次数。

1.2 Q-learning

Q-learning［11］是一种广泛应用于离散状态和动作空间的基于价值的无模型强化学习方法，采用时序差分方法优化一个可迭代计算的Q 值函数，定义如下：

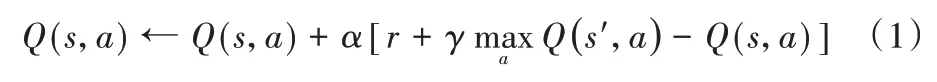
其中：Q（s，a）表示智能体在状态s下执行动作a获得的累积价值（Q 值）；r表示执行动作a后得到环境反馈的收益；s′是执行动作a后环境的状态；α为学习率，用来控制Q 值更新的快慢；γ为折扣率，决定时间的远近对收益的影响程度。

Q-learning 主要由四部分组成。1）Q 表：所有“状态-动作-累积价值”Q 值三元组的集合；2）探索/利用策略：智能体选择动作的方法，根据所处状态s决定采取哪种动作a；3）环境交互：智能体执行动作，并收集环境反馈的收益r；4）Q 表更新：利用执行的动作a、得到的收益r和环境新的状态s′按照式（1）更新Q 表。当所有Q 值三元组可以持续更新，整个学习过程就能够收敛。

1.3 因子分解机

FM［12］作为一种通用的矩阵分解模型，具有融合不同特征能力的强大的泛化性，被广泛应用在推荐系统领域。FM结合了支持向量机和因子分解模型的优点，能够在数据非常稀疏的情况下估算训练出可靠的参数，取得较好的预测和推荐结果［13］。

一般具体的因子分解机模型的应用取二阶交互，即特征的交互仅限两两交互模型。在理论上可以证明，随着交互度的增加，因子分解机模型的时间复杂度呈线性增长趋势。

2 基于因子分解机的Q表初始化方法

先验知识对于提高探索/利用策略的探索安全性起着至关重要的作用［14］。本文采用已探索的有限的Q 值三元组作为先验知识，基于FM 预测未知Q 值，提出了一种Q 表初始化方法。基于该初始化Q 表，智能体继续采用探索/利用策略与环境交互用，可提高Q-learning 的探索安全性。

2.1 问题描述

为了便于描述本文方法，将“状态-动作-累积价值”Q 值三元组定义如下。

令S为m个状态的集合，A表示n个动作的集合，Q表示m×n个Q 值的集合。

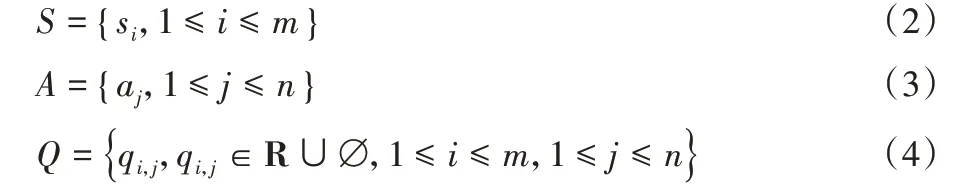
其中：si表示第i种状态；aj表示第j种行为；qi，j表示Q 值，即在状态si下执行动作aj获得的累积价值；∅表示未知Q 值。Q值三元组由（si，aj，qi，j）表示。

设Ω为Q 表中所有Q 值三元组集合，Δ为先验Q 值三元组集合，则Λ=Ω-Δ是未知Q 值三元组集合。Λ中价值qi，j将由Δ中的先验知识来预测。为更好地理解基于FM 预测未知Q 值的方法，一个简化的示例如图1 所示。

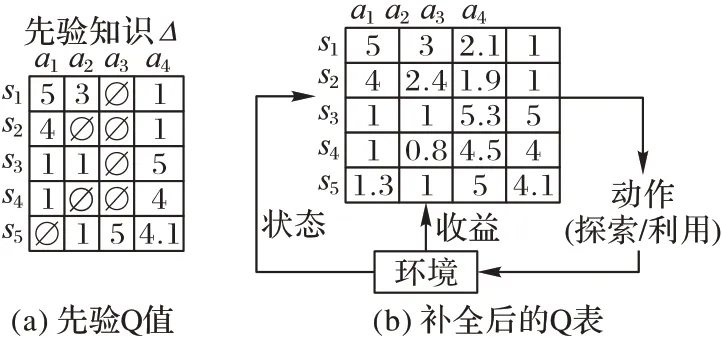
图1 基于先验Q值预测未知Q值Fig.1 Unknown Q-value prediction based on prior Q-values

假设Q 表包含5 种状态（s1，s2，s3，s4，s5）和4 种动作（a1，a2，a3，a4），共20 组Q 值三元组，如图1（a）为已获得的12 组先验Q 值三元组。基于已知的12 组先验Q 值三元组，对未知的Q值∅使用FM 方法进行预测，预测后的Q 表如图1（b）所示。预测后的Q 表可以引导智能体安全地探索未知的Q 值，减少其在探索过程中选择不良动作的次数。

2.2 算法模型

本文提出的基于FM 的Q 表初始化方法的核心思想是：利用FM 方法建立先验Q 值三元组中状态和动作之间潜在的交互作用模型来预测未知Q 值，以减少智能体在探索过程中选择不良动作的次数。

FM 可以通过分解参数利用二阶乃至更高阶的特征，在数据稀疏的情况下估算训练出可靠的参数。本文的方法采用二阶交互特征组合的FM 对先验Q 值三元组中状态和行动的交互作用进行建模：

模型输入的训练数据如图2 所示，图中每一行表示一个特征向量和其对应的目标，图中特征x由先验Q 值三元组中状态和行动的独热码组成。本文方法本质上是回归问题，因此选择均方误差作为损失函数评估模型的质量。本文方法的优化函数是最小化预测值与真实值的均方差函数，定义如下：

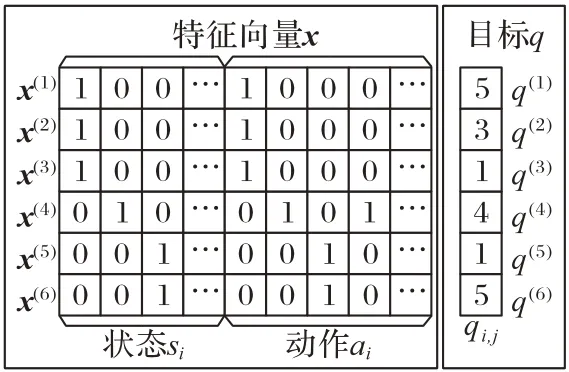
图2 输入数据示例Fig.2 Example of input data

其中：L(·)为损失函数；Ii，j用来标识qi，j是否为先验Q 值，若是则Ii，j=1，否则Ii，j=0。随后，采用随机梯度下降（Stochastic Gradient Descent，SGD）求解优化函数（7），估计模型参数θ：

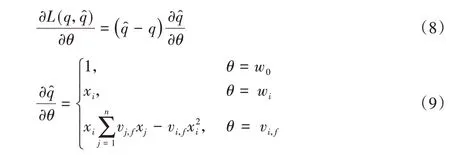
将已估计的模型参数θ代入式（5）中，便可以得到所有特征向量x的预测Q 值。

2.3 算法流程

本文方法伪代码如算法1。首先对Q 表中的状态和动作分别进行独热编码（第1）行）。由先验Q 值三元组中状态和动作的独热码构建特征向量x，对应Q 值作为算法目标q（第2）行）。然后利用式（8）、（9）求解优化函数（7）估计模型参数（第3）行）。再利用式（5）预测未知Q 值（第4）行）。最后将预测Q 值三元组与先验Q 值三元组合并为初始Q 表（第5）行）。

算法1 基于FM 的Q 表初始化。

输入 先验Q 值三元组（si，aj，qi，j），因子分解维度k；

输出 初始Q 表。

1）将S和A进行独热编码；

2）每个先验Q 值三元组，将si和aj的独热码作为特征矩阵，qi，j作为目标；

3）按照式（8）和式（9）估计参数θ={w0，w，V}；

4）按照式（5）预测未知Q 值；

5）合并先验Q 值三元组和预测Q 值三元组为初始Q 表。

3 实验及结果分析

3.1 实验环境

实验采用OpenAI Gym［15］中经典的网格强化学习环境Cliffwalk。该网格环境如图3 所示，共有48 种状态（每个网格一种状态），智能体有4 种行为（上、下、左、右）。强化学习的任务从起点（状态37）出发找到一条走到终点（状态48）的最优路径（累积收益最大）。在学习过程中，智能体每走一步能得到环境反馈的收益：若走到终点，无收益，游戏结束；走进灰色悬崖区域（状态38～47）将获得-100 的收益并回到起点；走到其他区域得到-1 的收益。

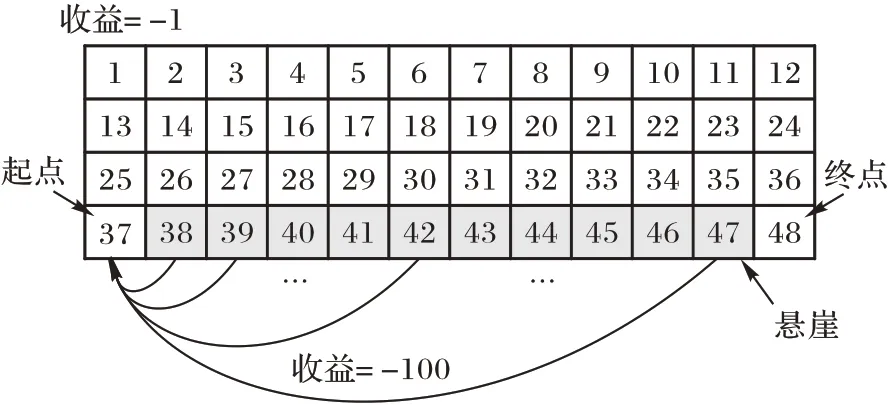
图3 Cliffwalk环境Fig.3 Cliffwalk environment

3.2 实验设计

从已收敛策略的Q 值三元组中随机采样作为先验知识，再采用不同探索/利用策略进行A/B 测试。一组为对照组，初始Q 表中除已采样先验Q 值外，其余均为默认值；另一组为实验组，基于先验Q 值使用本文方法对Q 表进行初始化。实验后，对比两组的探索安全性和收敛速度。

3.2.1 探索/利用策略

实验中采用三种常见的强化学习探索/利用策略进行智能体动作选择：

1）ε-greedy 策略。该策略在选取动作时有1-ε的概率选择当前策略评估下收益最大的动作（利用），而ε的概率随机选择动作（探索）。动作选择方式如下：

2）Boltzmann 策略［16］。该策略基于Q 值计算所有动作的概率分布，再依据概率分布来采样动作。该方法充分考虑不同动作a之间的优劣，让Q 值更高的动作a更容易被选中。概率分布计算式如下：

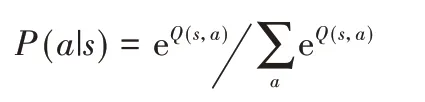
3）置信区间上界（Upper Confidence Bound，UCB）策略［17］。该策略的基本思想是乐观地面对不确定性，基于当前收益及探索次数为标准选择当前最优的动作来最大化置信区间上界。动作选择方式如下：

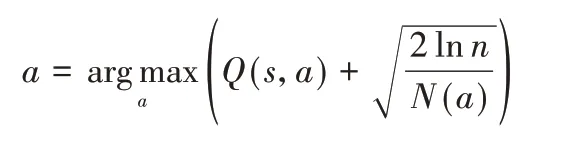
其中：n是已执行动作的总次数，N（a）是已执行动作a的次数。当幕数趋于无穷时，置信区间宽度趋近于0，Q 值预测会越来越准确。

3.2.2 实验参数

根据3.1 节可知，Cliffwalk 环境中Q 表共有192 组Q 值三元组，实验分别随机采样不同数量的Q 值三元组作为先验知识。每次随机采样后，对照组和实验组分别独立进行10 次实验，每次实验幕数为500 幕。实验中涉及的具体参数如表1。本文使用开源项目TuriCreate［18］对该问题进行建模。

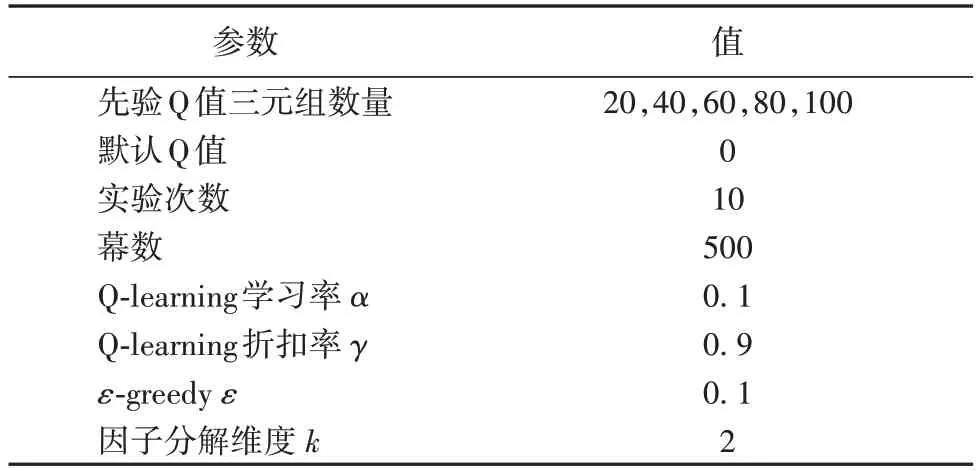
表1 实验参数Tab.1 Experimental parameters

3.2.3 评价指标

通过计算每一幕中动作平均收益来衡量该幕中的探索安全性。每一幕中的动作平均收益=总收益/行动总次数。

根据Cliffwalk 环境，若某一幕的动作平均收益小于-1，表明在探索过程中曾掉进过悬崖（访问状态38～47 之一），则认为该幕中的探索是不安全的即为一次不良探索，反之若动作平均收益等于-1，则认为探索是安全的。

3.3 结果分析

3.3.1 探索安全性

实验完成后，按照先验知识随机采样数量，分别统计对照组和实验组10 次实验中出现的不良探索幕数，结果如图4所示。从图4 中可以看出，使用本文方法的实验组相较对照组，不良探索幕数均有不同程度的减少，其中Boltzmann 和UCB 策略的不良探索幕数分别下降了68.12%和89.98%，分别如图4（a）和图4（b）所示，表明本文方法能有效利用先验知识提高智能体的探索安全性。由于ε-greedy 策略仅是盲目的、随机的选择动作，实验组相较对照组的改善不明显，且这两组总体不良探索幕数均明显高于其他两种策略，如图4（c）所示。

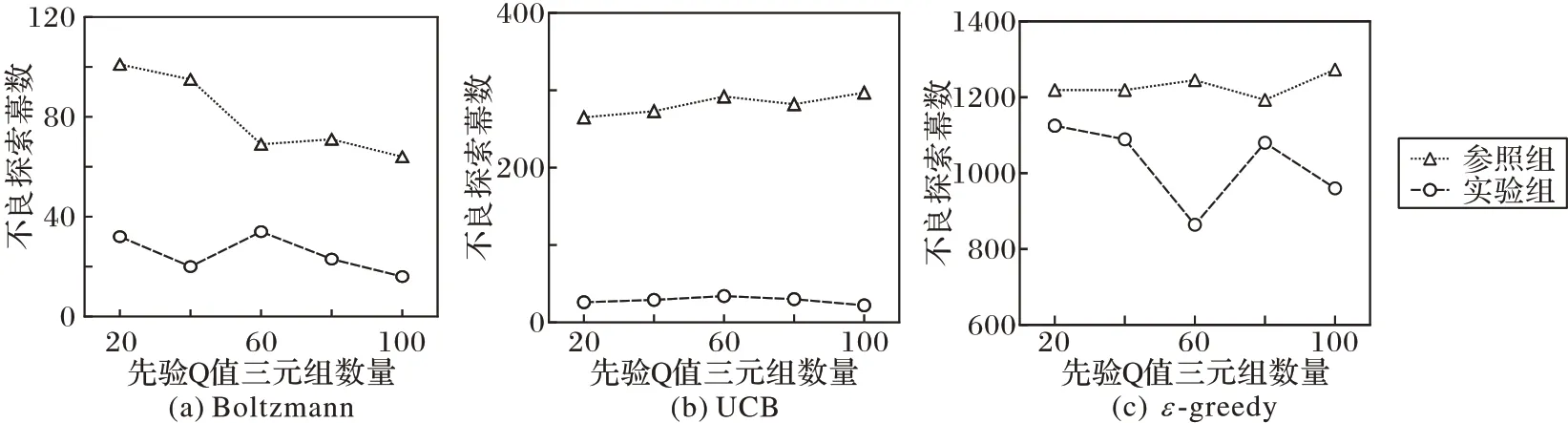
图4 不同策略探索安全性对比Fig.4 Exploration safety comparison of different strategies

3.3.2 收敛速度

图5～7 是在不同先验Q 值三元组数量下不同探索/利用策略每幕平均收益的结果。

实验组在三种探索/利用策略中均能快速收敛，尤其是在Boltzmann 策略和UCB 策略中，实验组比对照组的收敛速度更快，分别如图5 和图6。因ε-greedy 策略随机选择动作的特性，实验组和对照组收敛情况类似，在学习初期的平均收益要明显低于另两种策略，如图7。

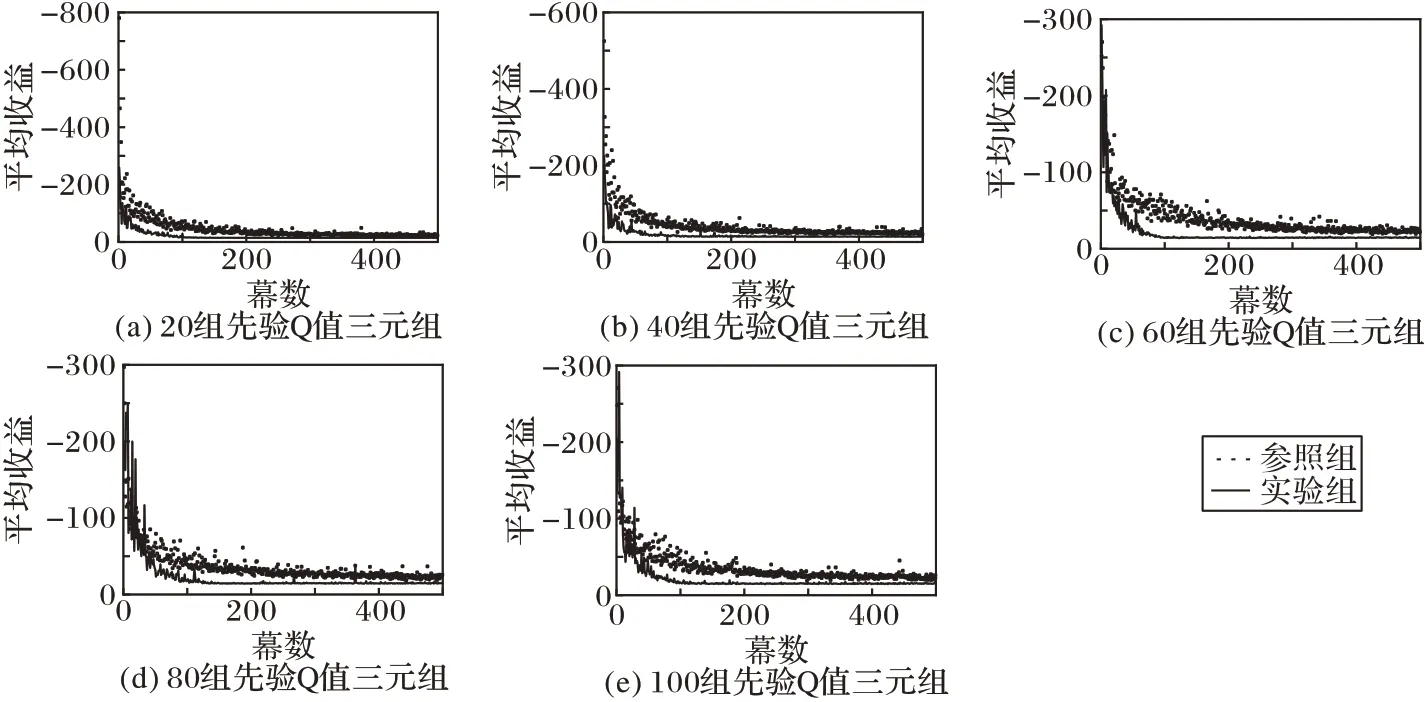
图5 Boltzmann策略收敛速度对比Fig.5 Comparison of convergence speed of Boltzmann strategy

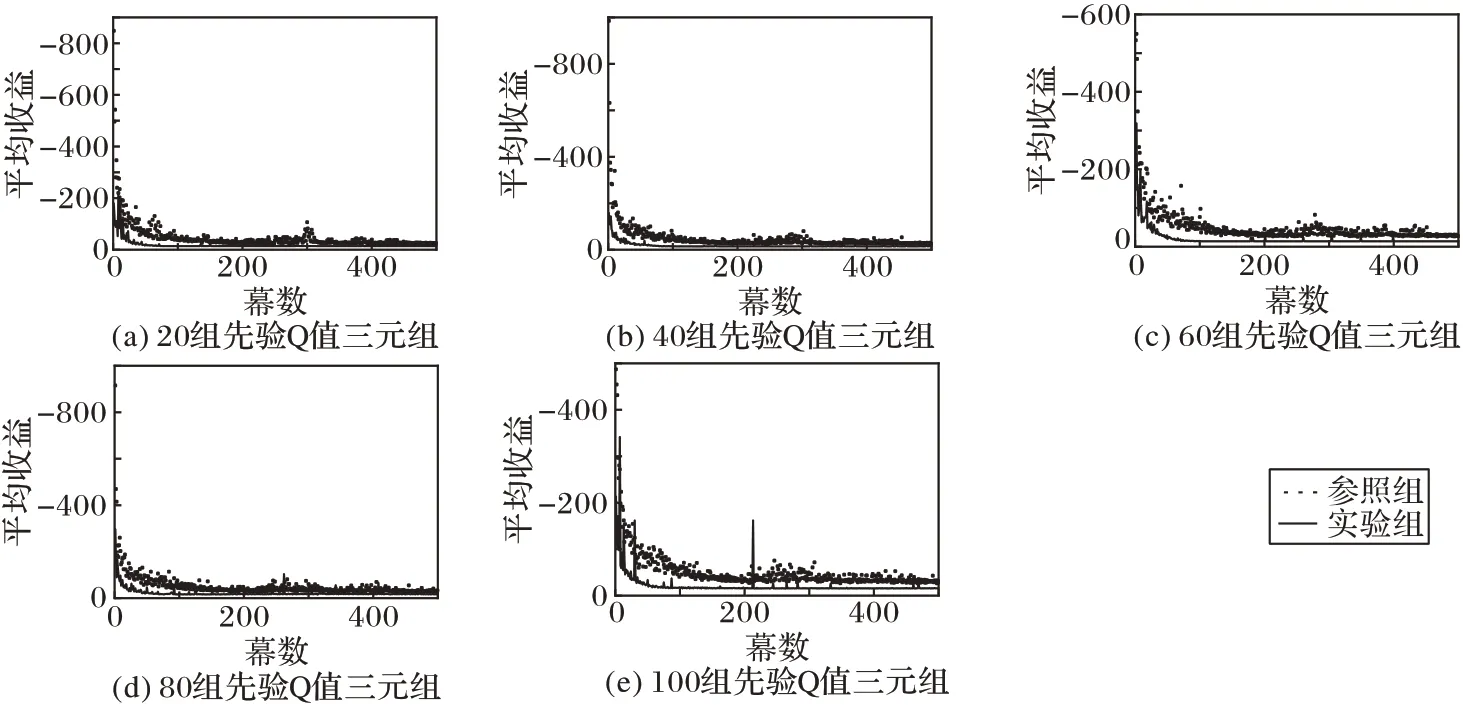
图6 UCB策略收敛速度对比Fig.6 Comparison of convergence speed of UCB strategy

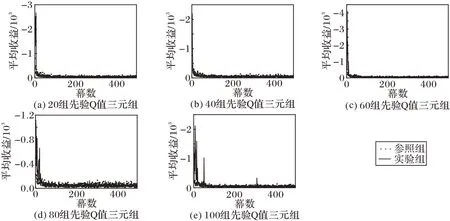
图7 ε-greedy策略收敛速度对比Fig.7 Comparison of convergence speed of ε-greedy strategy

4 结语

本文提出了一种用于Q-learning 安全探索的Q 表初始化方法。该方法利用FM 模型，构建先验Q 值三元组中状态与动作的交互作用模型，并通过该模型预测未知Q 值，进一步引导智能体探索。在OpenAI Gym 的强化学习环境Cliffwalk中进行A/B 测试，基于本文方法的Boltzmann 和UCB 探索/利用策略的不良探索幕数分别下降了68.12%和89.98%。实验结果表明，本文方法提高了传统探索/利用策略的探索安全性，同时提高了收敛速度。未来的工作将重点研究如何利用本文提出的方法提高深度强化学习DQN（Deep Q- Network）在连续空间的探索安全性。