基于逻辑单粒子的多方量子密钥协商协议

许盛伟，康 婕*

（1.北京电子科技学院，北京 100070；2.西安电子科技大学通信工程学院，西安 710071）

0 引言

经典密码学是基于数学复杂性而构建的，量子计算机的提出，使得计算能力大大增强，这对经典密码学构成了很大威胁。基于量子力学基本原理构建的量子密码学，在理论上具有无条件安全性，因此受到了很大的关注和研究。量子密钥协商（Quantum Key Agreement，QKA）是量子密码中一个重要分支，相较于量子密钥分发（Quantum Key Distribution，QKD），QKA 中每个参与者对最终共享密钥的贡献都一样，这使它对内部参与者攻击具有免疫能力，因此QKA 协议具有重要的研究意义。

2004 年，Zhou 等［1］基于量子隐形传态，提出了第一个两方QKA 协议；2013 年，Shi 等［2］基于Bell 态和Bell 测量，利用纠缠交换技术提出了第一个多方量子密钥协商（Multiparty Quantum Key Agreement，MQKA）协议。这两个协议提出之后，更多的QKA 和MQKA 协议［3-10］相继被提出。这些协议大多都基于理想环境，但在实际应用中，不可避免地会受到噪声的影响，因此噪声信道下的QKA 协议的设计具有重要的研究意义。2014 年，Huang 等［11］基于在集体噪声信道上共享EPR（Einstein-Podolsky-Rosen paradox）对的方法，提出的QKA协议可以不受集体噪声的影响。此后，一些可抗噪声的协议［12-17］被提出，其中，文献［12-15］都只涉及两方参与者；2018 年，Liang 等［16］基于逻辑W 态提出了一个可抗噪声的MQKA 协议，但是该协议效率较低；同年，Cai 等［17］利用多粒子纠缠态的特性，首次提出了两个可抵抗集体噪声的MQKA协议，但是该协议所需的量子资源多粒子纠缠态在实验上难以制备。

为了提出可抗噪声的高效MQKA 协议，本文以逻辑单粒子作为量子资源。为了抵抗集体退相位噪声和集体旋转噪声，本文分别提出了两组酉算符，将算符Uab（ab是算符的编码）作用在逻辑单粒子上，当a=0 时，不改变测量基；当a=1 时，则会改变测量基。利用此性质，提出了两个分别适用于集体退相位噪声和集体旋转噪声的MQKA 协议。

1 预备知识

首先，对量子密码协议用到的基础知识进行简单介绍；其次，介绍集体噪声以及可抗击噪声的逻辑量子比特；最后，针对可抗集体噪声的逻辑量子比特，定义了逻辑酉变换，并且介绍了该逻辑酉变换具有的特殊性质。

1.1 基础知识

1.2 集体噪声

1.3 逻辑酉变换

表1 酉算符作用在逻辑单粒子上的状态转化关系Tab.1 State transformation relationship of unitary operatoracting on logical single particle

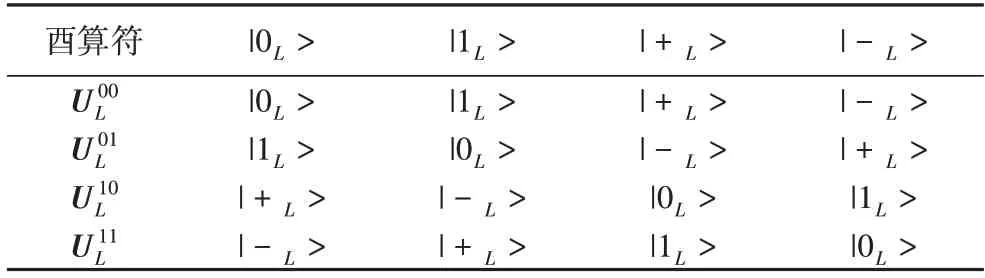
表1 酉算符作用在逻辑单粒子上的状态转化关系Tab.1 State transformation relationship of unitary operatoracting on logical single particle

2 协议描述

协议中，逻辑量子态|0dp＞、|+dp＞和酉操作U00、U10都对应于0，逻辑量子态|1dp＞、|-dp＞和酉操作U01、U11都对应于1。假设协议有N位参与者Pi(i=1，2，…，N)，协商过程如下。

2.1 初始化

步骤3 每位参与者Pi从{0dp，1dp，+dp，-dp}中随机选出足够多的诱骗逻辑量子比特，并把它们随机插入到逻辑单粒子序列Si→i+1中，得到一个新的混合序列，然后发送给他的下一位参与者Pi+1。

2.2 诱骗检测

步骤4 所有接收方Pi+1收到混合序列后，通过经典认证信道告知Pi，然后Pi公布诱骗粒子的位置与相应的制备基（{|0dp＞，|1dp＞}或{|+dp＞，|-dp＞}）。Pi+1则用正确的测量基去测量相应的诱骗粒子，并将结果告知Pi。Pi将测量结果和诱骗粒子的初始状态进行对比，算出错误率，根据错误率的值判断是否有窃听者存在。如果错误率低于预先设定的阈值，则认为没有窃听者存在，Pi+1删除所有的诱骗态粒子，恢复逻辑单粒子序列Si→i+1，并继续进行下一步；否则，认为存在窃听者，停止此次协议并重新开始。

2.3 加密和迭代加密

步骤8 重复上述加密阶段，直到所有的参与者Pi制备的初始态经过N-1 次传输到达Pi-1手中，也就是Pi-1得到混合序列之后，并成功通过诱骗态检测，然后删除逻辑诱骗粒 子，从而恢 复单粒 子序列。

2.4 获得共享密钥

步骤9 每位参与者Pi恢复出序列Si+1→i之后，公布这一事实，在所有参与者Pi都已确认收到编码后的序列之后，所有参与者Pi公 布Bi的 值。参与者Pi根 据Bi′(i′=1，2，…，n且i′≠i)的值，选择合适的测量基对Si+1→i中的每个逻辑粒子进行测量，测量结果记为。

步骤10 根据Bi′和Vi的值，每位参与者Pi可以计算其他N-1 个参与者密钥的异或和，进一步，可以得到最终的共享密钥K=Ki⊕Ki+1⊕Ki+2⊕…⊕Ki-1。

3 协议的正确性

下面以三个参与者协商为例，证明协议的正确性。

假设A、B、C 三位用户想要协商一个共享密钥。第一步，A 生成随机比特序列K1=01011 和B1=10011，B 随机生成K2=10010 和B2=00111，C 随机生成K3=10101 和B3=11010。按照步骤2，A 根据K1和B1，制备的初始态序列S1→2为|+dp＞|1dp＞|0dp＞|-dp＞|-dp＞。步骤5 中，B 对序列S1→2执行编 码操作U01⊗U00⊗U10⊗U11⊗U10，得到新的粒子序列S1→3为|-dp＞|1dp＞|+dp＞|0dp＞|1dp＞。步骤9 中，用户C 收到他的后一位参与者A 发来的经过编码的逻辑单粒子序列S1→3。

在A、B、C 公布Bi后，用户C 先根据B1和B2的值，选择的测量基为{|+dp＞，|-dp＞}，{|0dp＞，|1dp＞}，{|+dp＞，|-dp＞}，{|0dp＞，|1dp＞}，{|0dp＞，|1dp＞}，从而得到的测量结果V3为11001。最后，C 根据V3和自己的私钥K3，得到共享密钥K=K3⊕V3，即01100。用户B 和C 制备的初始态最终传送到A 和B 手中，由A 和B 来获取最终共享密钥，此协商过程见表2，其 中M1表示测量基{|0dp＞，|1dp＞ }，M2表示测量基{|+dp＞，|-dp＞}。

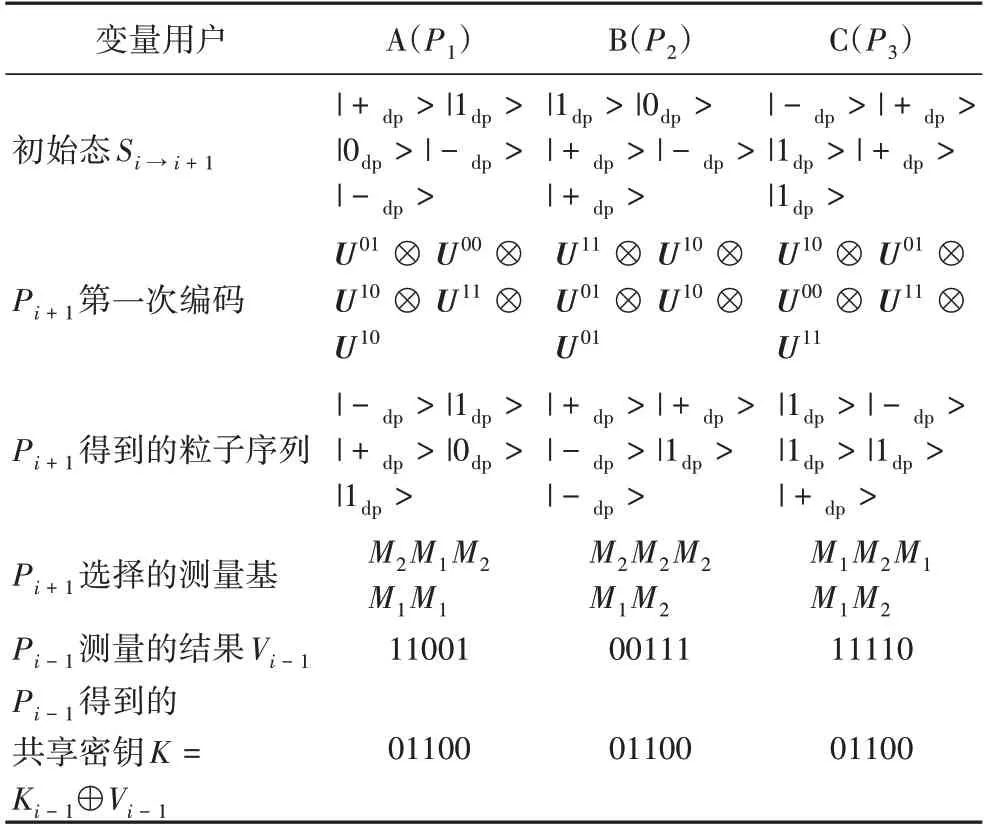
表2 三用户协议的协商过程Tab.2 Negotiation process of three-user protocol

4 安全性分析

4.1 截取重发攻击

假设Eve 是一个外部窃听者，为了执行截取重发攻击，他事先从{|0dp＞，|1dp＞，|+dp＞，|-dp＞}中，随机选择一些逻辑单粒子作为自己伪造的粒子序列，记为S′。在协议协商的过程中，Eve 拦截下Pi传输Pi+1的逻辑单粒子序列Si→i+1，然后将自己事先伪造好的粒子序列S′发送给Pi+1。但是，Eve不仅不知道诱骗粒子的位置和初始态，也不知道序列中每个逻辑粒子对应的测量基，所以Eve 伪造的粒子序列S′不可避免地将会干扰诱骗粒子的状态，在窃听检测过程中，Eve 会被发现。因此，该协议在截取重发攻击下是安全的。

4.2 纠缠测量攻击

纠缠测量攻击是一种常见的攻击策略，攻击原理是攻击者Eve 将自己事先准备好的一个辅助粒子序列与拦截的粒子序列相结合形成新的量子系统，然后执行酉操作UE使得辅助粒子序列和要传输的粒子序列产生纠缠关系，最后再将传输粒子重新发送给接收者，Eve 通过测量辅助粒子来获取有用信息。

假设Eve 事先制备了一些相同的逻辑辅助粒子|E＞，在本协议中，经过传输的只有逻辑单量子序列，所以Eve 想要执行纠缠测量攻击，只能将辅助粒子和逻辑单量子序列相结合，再执行酉操作，该操作可以表示为：

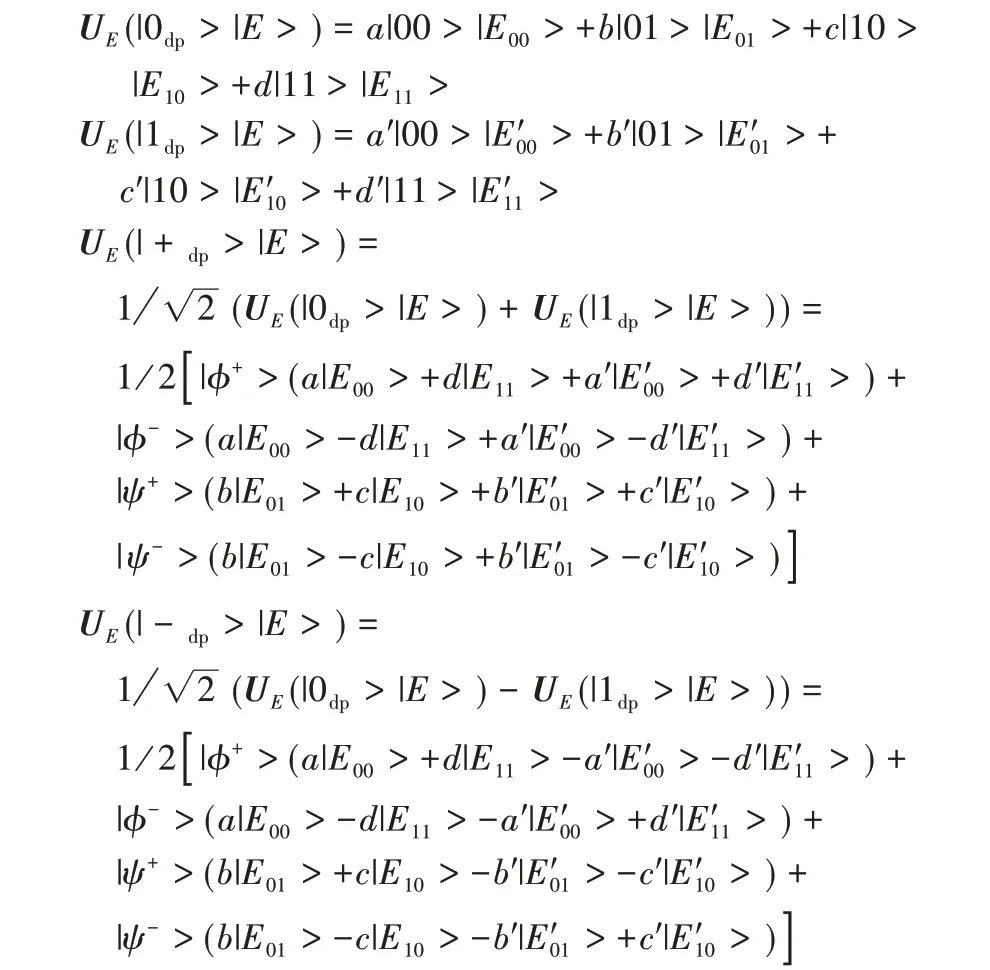
其中：|E00＞，|E01＞，|E10＞，|E11＞，|E′00＞，＞为纯态，为了保证UE为酉操作，则有：||a||2+||b||2+||c||2+||d||2=1，||a′||2+||b′||2+||c′||2+||d′||2=1。UE对|0dp＞|E＞的操作中，||b||2表示出现的结果不可变逻辑单粒子的状态|0dp＞，即结果为|01 ＞；得到结果为|00 ＞、|10 ＞、|11 ＞的概率分别是||a||2、||c||2、||d||2，这些都改变了原状态|0dp＞。类似地，UE对|1dp＞|E＞的操作中，||c′||2表示出现的结果不可变原状态|1dp＞，即得到结果|10 ＞；得到结果为|00 ＞、|01 ＞、|11 ＞的概率分别是||a′||2、||b′||2、||d′||2，这些都改变了原状态。

如果Eve想要顺利通过诱骗检测阶段，就必须满足：

所以，如果Eve 在诱骗阶段不想被发现，那么，他将获取不到有关共享密钥的任何信息。否则，Eve 的其他任何操作都将在窃听检测阶段被监测到，合法参与者将放弃此次协商协议重新开始，从而避免了Eve 的纠缠测量攻击。因此，该协议可以抵抗纠缠测量攻击。

4.3 参与者攻击

相较于其他攻击方式，参与者的内部攻击更具威胁性。参与者攻击是指多个不诚实的参与者事先自己协商一个密钥，在正式的协议协商过程中，他们相互合作，让这个密钥成为最终的共享密钥，然而诚实参与者对共享密钥没有任何贡献，这样就失去了密钥协商协议本应具有的公平性。

假设参与者Pi是诚实的，其他参与者Pi+1，Pi+2，…，Pi-1都不诚实，他们想要窃取Pi的私钥，使最终协商的密钥是他们事先约定好的，而没有Pi的参与。下面进行分析的时候，为了简便不考虑诱骗检测过程。

当传送的粒子序列是Pi制备的序列Si→i+1时，其他参与者不会从中获取任何Pi的私密信息，因为Si→i+1是Pi随机制备的，其中没有Pi的私钥编码信息。这一过程Pi没有编码。

当传送的粒子序列是Pi+1制备的序列Si+1→i+2时，Pi会根据自己的私钥Ki和随机序列Bi对序列Si+1→i进行编码，但是接下来发给Pi+1就已经结束了迭代加密过程，也就是说，与此同时Pi也收到了自己制备的粒子序列Si→i+1经过一圈编码之后的结果，其他参与者来不及协商。这一过程Pi的编码是最后一个。

当传送的粒子序列是除了Pi和Pi+1之外的其他参与者Pm(m=1，2，…，N，m≠i，m≠i+1）制备的序列时，真正和Pi有交流的只有Pi+1和Pi-1。这一过程中，Pi的编码处于中间位置。Pi-1制备了序列Si-1→i之后，将Si-1→i发送给Pi的同时将序列Si-1→i的状态告知Pi+1，在Pi对Si-1→i进行编码之后得到Si-1→i+1，并将Si-1→i+1发送给Pi+1。此时，Pi+1可以直接对序列Si-1→i+1进行测量，和Si-1→i的状态对比之后，就可以得到参与者Pi的编码；但是，他不知道Bi的值，也就不知道每个逻辑单粒子所对应的正确的测量基，所以他只能随机地选择测量基Zdp或者Xdp进行测量，这将会引入错误，引入错误的概率是12*12=14。因此，Pi将会有(1-(34)n)的概率检测到不诚实用户的存在。也就是说，在这一过程中，其他不诚实的参与者不能在完全不被检测到的情况下获得诚实参与者Pi的私钥。

上面的分析已经包含了协议协商的所有过程，所以该协议可以抵抗内部参与者攻击。

5 效率分析

本协议中，N位参与者最终协商了一个n比特长的共享密钥，每位参与者需要制备n个逻辑单粒子（n个逻辑量子比特，也就是2n个物理量子比特）和足够多的诱骗态粒子（假设每次制备n个逻辑诱骗态，即2n个物理量子比特，共制备N次）；除此之外，每位参与者还需要制备n比特长的经典随机序列，并公布n比特的经典信息。所以，该协议中每位参与者需要使用2(n+Nn)个物理量子比特信息和2n比特的经典信息。因此，协议的量子比特效率为：。表3 中，将本文所提出的MQKA 协议和已有的协议进行比较，可以看出，在可抗噪声的MQKA 协议中，和文献［16-17］相比，本协议有较高的量子比特效率；而且相较于文献［16-17］用到的逻辑W 态和多粒子纠缠态，本协议的逻辑单粒子制备更容易。

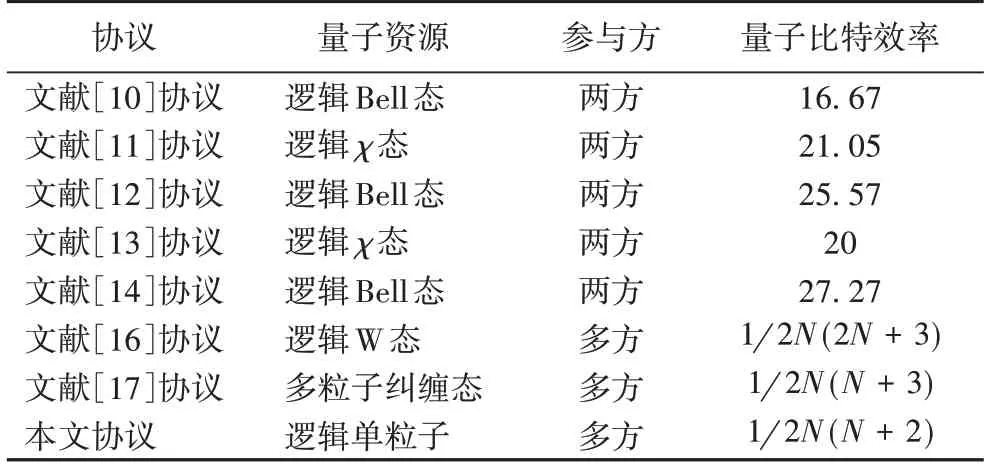
表3 多种可抗噪声协议的效率比较Tab.3 Efficiency comparison of several anti-noise protocols

6 结语

本文针对集体退相位噪声和集体旋转噪声，分别设计了两组酉算符，使得每组酉算符作用在相应的逻辑单粒子上时，状态的改变会有改变测量基或者不改变测量基两种情况，这就使最终测量时需要确定正确的测量基，利用这一性质提出了一种多方量子密钥协商协议。

类比于Pauli 算子对单粒子的作用，针对逻辑单粒子，定义了相应的逻辑酉变换，将逻辑单粒子作为量子资源，相较于文献［16］的逻辑W 态和文献［17］的多粒子纠缠态，减少了对量子资源的消耗。测量基是否发生改变和所选取的逻辑门有关，这一性质可有效抵抗内部参与者攻击：假设不诚实的参与者相互合作窃取了诚实参与者编码前后的粒子，他们不知道诚实参与者私钥加密后测量基是否变换，因此无法选择正确的测量基，就不能窃取诚实参与者的私钥信息。

最后通过安全性分析证明本协议可以有效抵抗包括参与者攻击在内的几种常见的攻击；通过效率分析，证明了本协议在使用了逻辑单粒子这一容易制备的量子资源的基础上，具有较高的量子比特效率。和普通的量子密钥协商协议相比，可抗噪声的量子密钥协商协议效率还是较低，还需要进一步研究。