基于准确率爬坡的动态加权集成分类算法

李小娟，韩 萌，王 乐，张 妮，程浩东

（北方民族大学计算机科学与工程学院，银川 750021）

0 引言

集成学习由于其较高的分类准确性和能够快速适应概念漂移等特点，成为了数据流分类研究的主要方法之一［1］。它使用多个弱分类器构成一个强分类器，弱分类器有决策树、支持向量机、神经网络等［2］；基分类器之间的整合方式有简单加权投票、多数投票、随机投票等［3］。与仅仅使用单个算法相比，集成学习方法能获得更好的性能［4］。集成学习一般分为Bagging、Boosting 及Stacking 三类。

杠杆装袋（Leveraging Bagging）算法［5］是一个比较经典的数据流集成分类算法，其将装袋（Bagging）的简单性与向分类器的输入和输出添加更多随机化相结合，可以更好地降低相关性、增加多样性，具有更高的准确率。推算特征选择装袋（Imputed Feature selected Bagging，IFBag）算法［6］使用多重插补、特征选择和装袋集成学习方法来构造基分类器，以对新的不完整实例进行分类。权重更新分类（Weight Update Classifiers，WUC）［7］是对自适应装袋方法的修改，这种修改不会在每次迭代中更新部分分类器，而是基于计算出的权重，采用性能最差的n个分类器（具有最高错误率）并仅更新那些分类器，其他集成成员保持不变。基于概念漂移检测的网络数据流自适应分类算法［8］通过比较滑动窗口中的数据与历史数据之间分布差异来检测概念漂移，然后对窗口数据进行过采样以减少样本之间的不平衡，最后将处理后的数据集用于在线学习的分类器，它更新分类器以应对数据流中的概念漂移。Voting-Boosting［9］是一种使用投票和Boosting 的集成方法，用于特征的最佳选择和预测。为了进行特征选择，除投票、Boosting 之外，还使用了最佳优先搜索算法。在线Boosting（Online Boosting，OLBoost）算法［10］使用极快决策树（Extremely Fast Decision Tree，EFDT）作为基学习器，以便将它们整合为一个强大的在线学习器。DSTARS（Deep Structure for Tracking Asynchronous Regressor Stacking）［11］是一种新颖的多目标回归（Multi-Target Regression，MTR）方法，将多个堆叠回归器组合到一个深层结构中来扩展堆叠单目标（Stacked Single-Target，SST）方法；通过不断改进对目标的预测来提高预测性能。此外，DSTARS 通过跟踪异步数量的堆叠回归量来单独利用每个目标的依赖性。FASE-AL（Fast Adaptive Stacking of Ensembles using Active Learning）算法［12］是对快速自适应Stacking 集成（Fast Adaptive Stacking of Ensembles，FASE）算法的改进，使用主动学习诱导具有未标记实例的分类模型。SSEM（Self-adaptive Stacking Ensemble Model）［13］是一种新的自适应Stacking 集成算法，该算法选择性地集成了不同基学习器，并通过遗传算法自动选择了最佳基学习器组合和超参数。

尽管现有的集成分类算法能够很好地处理数据流问题，但是，在数据流集成分类中仍有很多问题需要解决，例如：集成数目的更新方式、为基分类器分配合适的权值等。针对上述问题，本文提出了两种新的集成分类算法，主要工作如下：

1）设计了一种准确率爬坡集成分类算法（accuracy Climbing Ensemble Classification Algorithm，C-ECA）。C-ECA改变了传统集成学习方法中基分类器的更新方式，不再替换相同数量的基分类器。该算法首先会初始化一个分类器池Π，大小设置为N（N＞1）；然后，向大于N的方向（上坡）和小于N的方向（下坡）进行搜索，确定最佳集成数目。

2）设计了基于爬坡的动态加权集成分类算法（Dynamic Weighted Ensemble Classification Algorithm based on Climbing，C-DWECA）。在实际训练实例时，不同基分类器在不同数据流上的预测性能存在差异，所以，需要对不同基分类器分配合适的权值。因此，本文在C-ECA 的基础上，设计了一个新的加权函数w(x)，从而得到C-DWECA，算法在分类准确率方面得到了很大的提升。

3）采用快速霍夫丁漂移检测方法（Fast Hoffding Drift Detection Method，FHDDM）来检测概念漂移。

1 相关工作

数据流具有许多固有属性，包括连续有序到达、无限长度、概念漂移等［14］。因此，构建更健壮的模型以迅速有效地从数据中提取有意义的信息变得更加重要。

数据流中的概念漂移问题是指数据流的基础分布会随时间动态变化。现有的分类方法主要采用两种策略来解决概念漂移问题：一种是被动方法，该方法基于遗忘机制（即动态窗口或衰减函数）或定期检测每个传入数据实例分类器的分类性能，以决定何时更新过时的分类器［15-16］。另一种是主动方法，该方法侧重基于分布的检测或基于序列的方法［17-18］。

在处理实际问题的时候，会出现不同类型的概念漂移。当分类决策边界改变时发生的概念漂移称为真实概念漂移，当分类决策边界不发生变化时称为虚拟概念漂移，真实概念漂移与虚拟概念漂移分布类型如图1 所示。

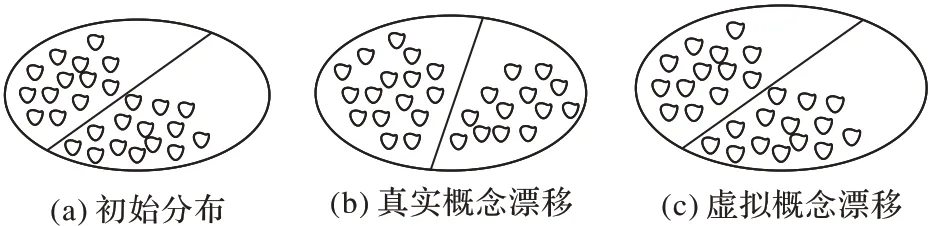
图1 真实概念漂移与虚拟概念漂移分布类型Fig.1 Distribution types of real concept drift and virtual concept drift

现阶段对于概念漂移的研究还没有一个统一的描述，除真实概念漂移和虚拟概念漂移之外，研究人员还根据概念漂移变化速度将概念漂移分为突变漂移、渐变漂移、重复漂移和增量漂移［19］。突变漂移是指数据流发生巨大的变化从一种状态变换到另外一种状态；渐变漂移是指随着时间的变化数据流逐渐变化；重复漂移是指概念在特定的时间段反复出现；增量漂移是指随着时间的推移概念缓慢变化。基于变化速度的概念漂移分布类型如图2 所示。

图2 基于变化速度的概念漂移类型Fig.2 Types of concep drift based on speed of change

2 C-ECA和C-DWECA

为了方便对算法进行描述，本文首先对问题进行了规范化。设数据流S={x1，x2，…，xt}是一个批处理序列，其中xt表示第t个传入集成中的数据实例。数据流传入集成中之后，通过m个基分类器进行训练，将m个结果融合共同决策，得到最终的决策结果。

2.1 C-ECA

C-ECA通过准确率对集成数目进行更新。图3（a）展示了传统集成分类算法中基分类器的更新方式，在更新前后，基分类器数目保持不变；图3（b）、图3（c）展示了本文基分类的更新方式。其中，在上坡学习时，训练基分类器后，基分类器数目增加；在下坡学习时，训练基分类器之后，基分类器数目减少。

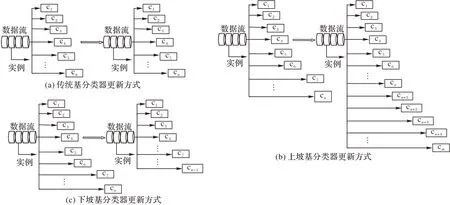
图3 基分类器更新方式Fig.3 Base classifier update methods

C-ECA 与一些传统的集成分类方法一样，都是使用霍夫丁树作为基分类器构建集成。在传统集成分类算法中，集成数目设置为固定值，通过替换相同数量的基分类器对集成进行更新。例如，在自适应多样性的在线增强（Adaptable Diversity-based Online Boosting，ADOB）算法［19］中，集成数目为10，在基分类器更新时，通过比较准确率，添加一个新的基分类器，并且删除一个性能最差的基分类器；在IBS 算法［20］中，在比较准确率之后，一次添加多个基分类器，同时删除相同数量的基分类器。C-ECA 则是以分类器池中N个基分类器为起始，在基分类器更新时，通过比较准确率，一次添加一个基分类器，在右边区间内确定准确率最高时集成数目；同时，在左边区间确定准确率最高时集成数目，在进行比较之后，确定最佳集成数目。

图4 是C-ECA 示意图，该算法首先创建一个分类器池Π，对实例进行训练；在输入数据流时使用FHDDM 概念漂移检测器进行检测，如果发生概念漂移，则将当前的数据流实例缓存到窗口，重置当前基分类器，使用窗口中的实例重新训练基分类器，加入分类器池。C-ECA 根据准确率对基分类器进行更新，在增加基分类器时，遵循一次增加一个基分类器的原则，在增加的同时也会将权值小于阈值Θ的基分类器进行删除；在减少基分类器时，根据阈值删除性能最差的基分类器；最后，确定最佳集成数目。

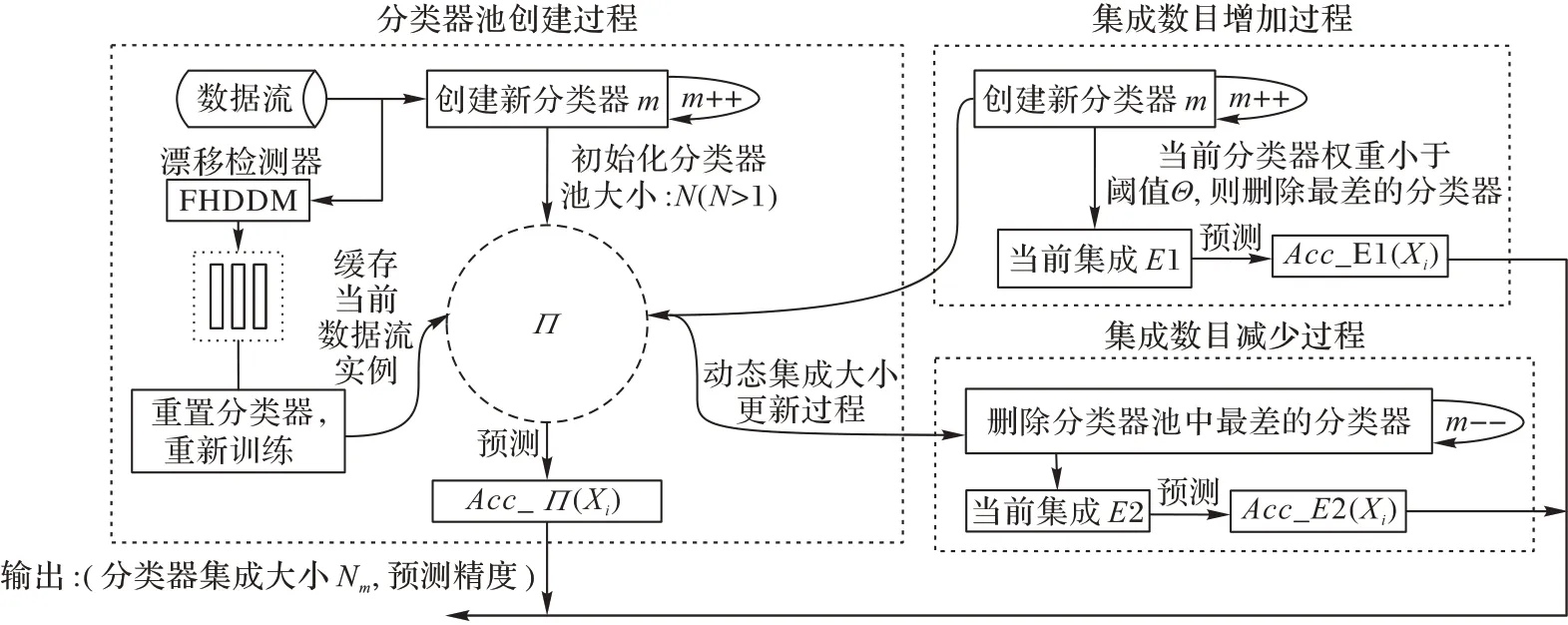
图4 C-ECA示意图Fig.4 Schematic diagram of C-ECA algorithm

2.2 C-DWECA

相较于C-ECA，C-DWECA 同样根据准确率来判断是否向集成中添加或删除基分类器。C-DWECA 在C-ECA 的基础上提出了一个加权函数w(x)，w(x)为不同数据流对应的基分类器最佳权值，根据数据实例被正确分类权值和被错误分类权值对权值进行调整，改变基分类器原来的权值，从而达到提高算法准确率的目的。

AWDOB（Accuracy Weighted Diversity-based Online Boosting）［21］是基于准确率加权的集成分类算法，在数据流中频繁发生目标分布变化时提高基分类器的准确率，通过引入一个准确率加权方案，使用当前基分类器的准确率以及所有基分类器正确分类和错误分类的实例总和，将当前基分类器的权值分配给数据流中当前实例。基分类器的权值计算如式（1）、（2）所示：

C-DWECA 通过对基分类器权值w(x)的控制，在不同数据流上依据准确率对w(x)进行动态调节，根据实例xt被正确分类权值Wr和错误分类权值Wc，向其中添加加权函数w(x)，如式（3）、（4）所示：

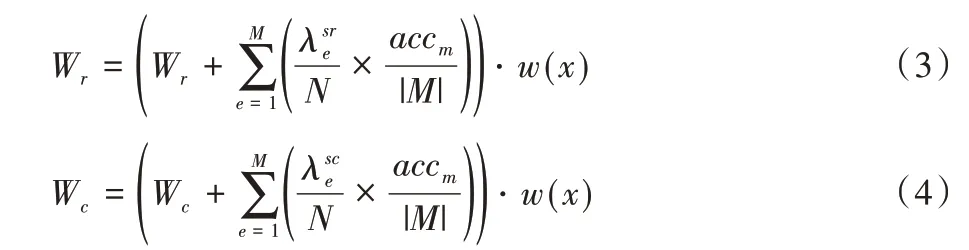
其中：Wr表示正确分类实例的权值，Wc表示错误分类实例的权值表示基分类器正确分类的实例总数，表示基分类器错误分类的实例总数；N表示到目前为止在数据流中看到的实例数；accm表示当前基分类器的准确率；M表示集成数目。

式（3）、（4）是对基分类器权值更改的具体过程，式（6）是式（5）的推算过程。数据流实例被正确分类和被错误分类所占的比例是通过追踪每个基模型正确分类和错误分类的训练实例（分别为Wr和Wc）的总权重并使用它们来更新每个基模型的误差εe来完成的。μt是对误差率εe归一化处理，wf是第t个基分类器通过加权函数最终分配权值，分别如式（7）、（8）。

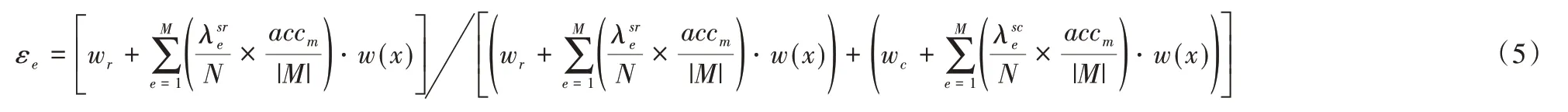
进行归一化处理：

加权函数w(x)是不同数据流中基分类器对应的最佳权值，w(x)函数如式（9）所示：

算法第1）～6）行先传入数据流S，初始化分类器池的数量N，初始化权值w，创建新的基分类器m，并利用分类器池进行预测，然后使用FHDDM 进行概念漂移检测。第7）～16）行是上坡的过程，先创建一个新的基分类器，加入分类器池中，根据本文所提出的式（3）、（4）计算正确分类实例的权值和错误分类实例的权值；之后判断分类器池中是否存在权值小于阈值Θ的基分类器，如果存在则删除此基分类器，否则直接进行预测；最后利用更新后的基分类器池进行预测并进行概念漂移的检测。第17）～26）行是下坡的过程，算法直接根据阈值来删除性能最差的基分类，利用更新后的分类器池进行预测并检测概念漂移。最后，输出分类器池中基分类器的数量，即集成数目Nm与准确率。

2.3 概念漂移的处理

本文使用了FHDDM 概念漂移检测方法作为概念漂移检测器，具有更好的性能。其中处理概念漂移的伪代码如算法2 所示。

算法2 FHDDM概念漂移检测方法。

算法第1）行将窗口大小设置为n；第2）行初始化delta；第3）行计算阈值ε；第4）行重置窗口与μm值（μm为正确分类的最大平均值）；第5）～8）行如果窗口为满，则从尾部丢弃一个实例，并在窗口头部插入一个实例；第9）行计算窗口内正确分类的平均值；第10）～12）行更新μm值；第13）～18）行如果窗口内正确分类平均值与最大平均值之差大于阈值ε，则表明发生了漂移，执行重置过程。

3 实验结果与分析

本文实验硬件环境是Intel Core i7 2600k+256 GB RAM的PC，操作系统是Windows 10 专业版，软件环境是大规模在线分析（Massive Online Analysis，MOA）开源平台［22］，所有实验数据流全部由MOA 生成。

3.1 数据流

Agrawal 数据流包含了1 000 000 条数据实例，10 条属性，2 个类标签（groupA，groupB），数据流Agrawal-1、Agrawal-2、Agrawal-3 是对Agrawal 数据流中的某些参数修改之后得到。function 表示使用的分类功能；InstanceRandomSeed 表示随机生成实例的种子；peturbFraction 表示引入数字值的干扰量（噪声）。其中，各个参数的具体设置值如表1 所示。Hyperplane-1 数据流包含了500 000 条数据实例，11 条属性，2个类标签（class1，class2）；Hyperplane-2、Hyperplane-3 也是通过数据流Hyperplane 得到的，其中，具体的参数设置如表2 所示。InstanceRandomSeed 表示随机生成实例的种子，numAtts表示要生成的属性数，默认值为2；numDriftAtts 表示具有概念漂移的属性；noisePercentage 表示要添加数据中的噪声比，默认值为5。Wave 数据流包含了22 条属性，3 个类标签（class1，class2，class3）；其中，前面的21 个属性均在实数的范围内取值。SEA 数据流是合成数据流，包含了4 条属性，2个类标签（groupA，groupB）；它是由3 个随机生成的实数特征和2 个正负类别组成的，可以通过改变参数的值来引入概念漂移。LED（Light Emitting Diode）数据流具有概念漂移的特性，包含25 条属性，其中前24 条属性是布尔类型。RandomRBF 数据流包含了500 000 条实例，11 条属性，以及5个不同的类标签。

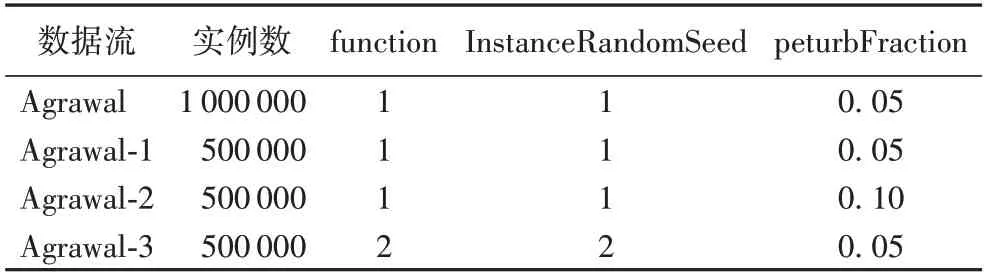
表1 Agrawal数据流参数Tab.1 Parameters of Agrawal data streams

表2 Hyperplane数据流参数Tab.2 Parameters of Hyperplane data streams

3.2 分析结果

3.2.1 集成数目对准确率的影响

在传统的集成学习算法中，不管是一次更新一个基分类器还是一次更新多个基分类器，都是对基分类器进行了替换，更新前后集成数目不变。本文提出的算法不是对基分类器进行替换，而是根据准确率对基分类器进行更新，确定最佳集成数目。

图5（a）～（d）是C-ECA 在Wave、SEA、Hyperplane-1、Agrawal-1 数据流上对准确率的影响。从图中可以看出在Wave 数据流上，当集成数目为6 的时候，算法的准确率最高（85.38%）；在SEA 数据流上，集成数目为5 时，准确率最高（89.65%），在Hyperplane-1 数据流上，集成数目为2 时，算法的准确率最高（91.72%）；C-ECA 在Agrawal-1 数据流上，集成数目为12 时算法准确率最高（94.64%）。图5（e）～（g）是C-DWECA 在Agrawal-2、SEA、随机径向基函数数据流（Ramdom Radial Basis Function，RamdomRBF）上对准确率的影响。当集成数目为17 时，算法在Agrawal-2 数据流上准确率最高，为94.24%；在SEA 数据流上，当集成数目为12 时，算法准确率最高；在RamdomRBF 数据流上，集成数目为11时，算法准确率最高。总体来说，C-ECA 大多在集成数目小于10 的时候，算法准确率能达到最高，但在Agrawal-1 数据流上集成数目大于10 的时候算法准确率最高；S-DWECA 算法则是在集成数目大于10 的时候，算法准确率达到最高。

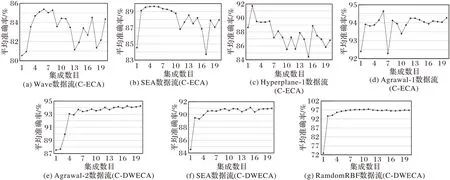
图5 集成数目对准确率的影响Fig.5 Influence of ensemble number on accuracy

3.2.2 算法准确率对比

将C-ECA 与12 个对比算法在11 种不同的数据流上进行实验，详细结果见表3，其中，准确率最高的数值都用粗体表示。从准确率方面来进行分析，C-ECA 在Agrawal数据流上集成数目为12时，除了C-DWECA、LimAttClassifier 算法之外，准确率均高于其余的算法 ；在 RandomRBF（RandomRBFGenerator）数据流上集成数目为10 时，除CDWECA、杠杆装袋（Leveraging Bagging，LevBag）、自适应随机森林（Adaptive Random Forest，ARF）算法之外，算法准确率均高于其余算法。在Wave 数据流上准确率高于ADOB、BOLE（Boosting-like Online Learning Ensemble）、OzaBoost（Oza and Russell’s online Boosting）、AUE2（Accuracy Updated Ensemble）、OAUE（Online Accuracy Updated Ensemble）、LevBag（Leveraging Bagging）、OCBoost（Online Coordinate Boosting）、ADACC（Anticipative and Dynamic Adaptation to Concept Changes）、LimAttClassifier（combining restricted hoeffding tees using stacking）。在SEA（SEAGenerator）数据流上C-ECA 的集成数目为9，算法的准确率高于ADOB、BOLE、OzaBoost、ADACC、LimAttClassifier。在LED 数据流上算法的集数目小为10 时，准确率高于ADOB、BOLE、OzaBoost、OAUE、LevBag、OCBoost、ADACC、LimAttClassifier。

表3 C-ECA、C-DWECA与不同对比算法的准确率对比 单位：%Tab.3 Accuracy comparison among C-ECA，C-DWECA and different comparison algorithms unit：%

C-DWECA 是在C-ECA 的基础上进行修改的，算法在准确率方面得到了很大的提升。C-DWECA 在本文所提到的11个数据流中准确率均最高。在Agrawal、Agrawal-1、RandomRBF 数据流中，C-DWECA 的准确率分别达到了97.24%、97.29%、97.44%；在Agrawal-3 数据流上，算法的准确率比ADACC 算法提升了49%，比BOLE 算法提升了21%，比OCBoost 提升了26%，比LimAttClassifier 提升了30%；在Hyperplane-1 数据流中，算法的准确率比ADOB 提升了近86%，比LimAttClassifier 提升了18%；在Hyperplane-2 数据流上，算法的准确率比ADOB 提升了50%，比ADACC 提升了15%，比LimAttClassifier 提升了21%；在Hyperplane-3 数据流上，算法的准确率比ADOB 提升了85%，比LimAttClassifier 提升了18%；在Wave 数据流上，算法的准确率比ADOB 提升了175%，比ADACC 提升了17%；在LED 数据流上，C-DWECA的准确率达到了80.42%，而对比算法中，ADOB 的准确率仅有9.98%，准确率相对较高的是ARF 算法（74.21%），并且比ADACC 的准确率提升了39%；在SEA 数据流上，C-DWECA的准确率达到了91.07%，均高于其余的对比算法。

Agrawal 数据流中，peturbFraction 表示具有噪声属性，C-ECA、C-DWECA 能很好地处理噪声数据，在Agrawal 数据流上，除C-DWECA、LimAttClassifier 算法外，C-ECA 的准确率均高于其余算法；C-DWECA 的准确率则高于所有对比算法。同样地，在数据流Agrawal-1、Agrawal-2、Agrawal-3 数据流上，两个算法也表现出了很好的性能。Hyperplane 数据流具有概念漂移、噪声属性，C-ECA、C-DWECA 在Hyperplane 数据流上也表现出很好的性能。SEA、LED 数据流都有概念漂移的属性，C-ECA、C-DWECA 均可以很好地处理概念漂移，在SEA、LED 数据流上准确率都比较高。

表4 展示了算法在11 个数据流上的平均准确率，从表中可以看出本文所提出的C-DWECA 的平均准确率达到了92.60%，其中，C-DWECA 的平均准确率比ADOB 提升了40%，比OCBoost 算法提升了18%，比ADACC 算法提升了18%，比LimAttClassifier 算法提升了14%。为了能更直观地对算法的准确率进行比较分析，绘制了在数据流Agrawal-1、Agrawal-2 上的折线图。其中，在图6 中考虑到图示的效果，所以一些准确率较低的算法没有在图中进行展示；从图6 中可以看出，本文所提出的C-DWECA 在准确率方面明显优于其他对比算法，并且可以同时适应带有概念漂移和噪声的流数据，整体性能表现优异。

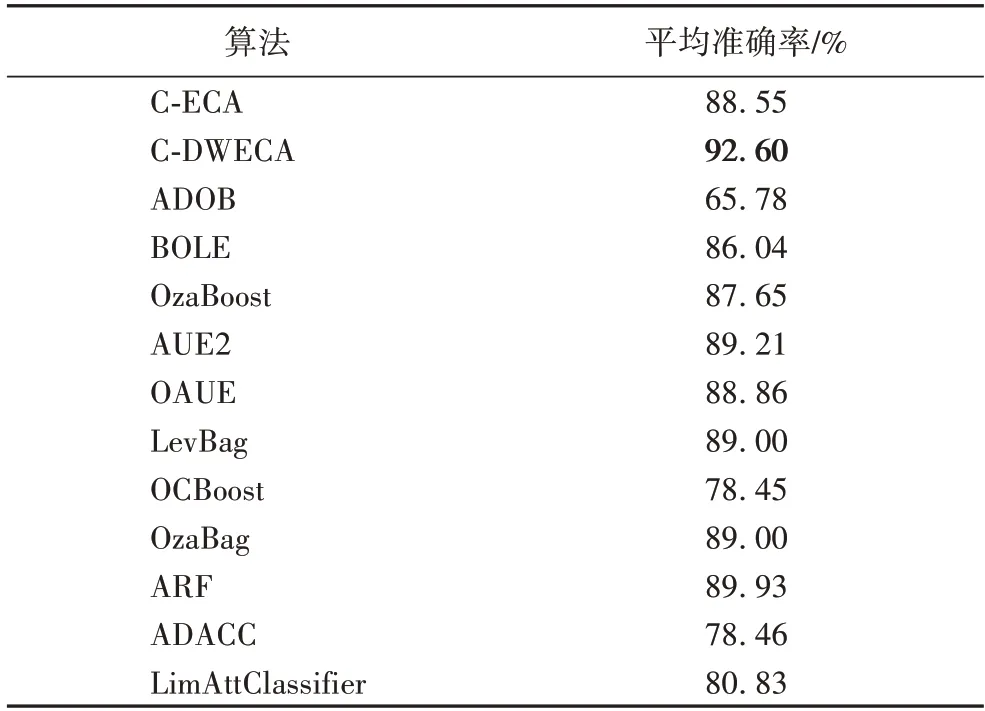
表4 不同算法的平均准确率Tab.4 Average accuracies of different algorithms

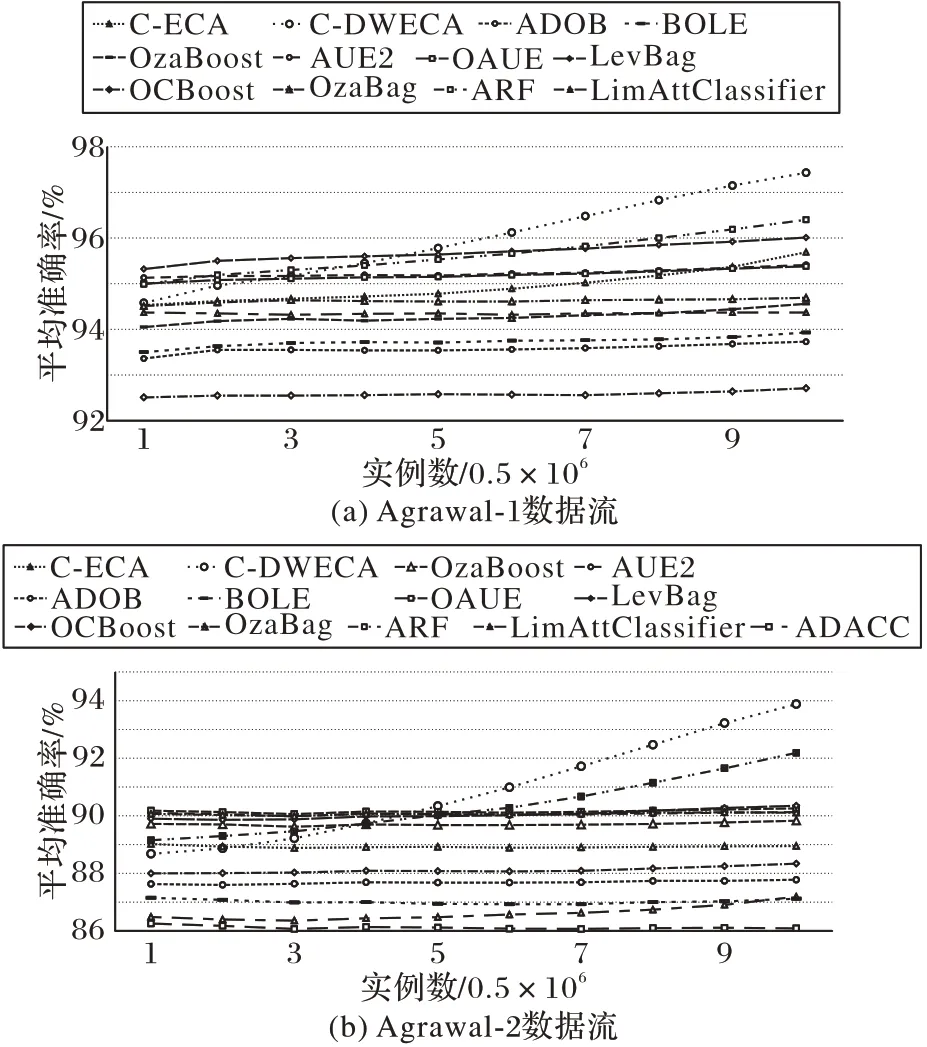
图6 不同算法准确率对比Fig.6 Accuracy comparison of different algorithms

3.2.3 生成树的规模以及时间效率比较

在实验的过程中发现，生成树规模的大小也是衡量算法性能的一个重要的指标，本节的主要目的是验证C-ECA 在各个数据流上树生成规模表现出来的优异性能。ADOB 算法在几种数据流上准确率表现得相对较低，ARF、ADACC 以及LimAttClassifier 算法在实验过程中树的性能表现不稳定。由于树规模的研究是在准确率差别不大，以及生成树的规模相对稳定的条件下进行研究的，所以，本节不对这几种算法进行研究。算法分别在Agrawal、Hyperplane、Wave、SEA、LED、RandomRBF 数据流上进行了实验，数据实例均为50 000 条，实验结果如图7 所示。

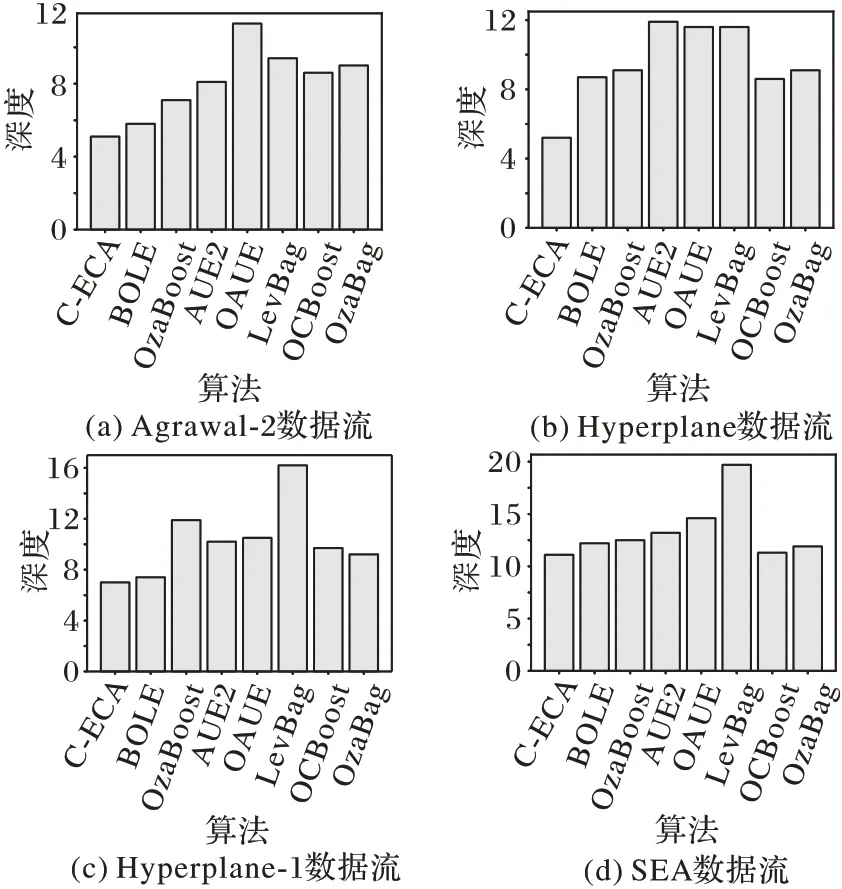
图7 不同算法的生成树深度对比Fig.7 Spanning tree depth comparison of different algorithms

C-ECA 在5 个数据流上树的深度表现都很优秀；在Agrawal-2 数据流上，C-ECA 树的深度为5.1，相较其余的算法均小一点，比起OAUE 算法，C-ECA 表现出了令人惊喜的结果；同样在Hyperplane 数据流上，C-ECA 在树的深度方面也表现得最优异，比起AUE2 算法，C-ECA 树的深度减小了6.7；在SEA 和LED 数据流上，C-ECA 也表现出了令人欣喜的优势。在RandomRBF 数据流上，C-ECA 的树的深度也比AUE2、OAUE、LevBag 和OzaBag 算法表现得要好。

表5 主要展示了算法的时间效率的结果，从表中可以看出C-DWECA 在时间效率上表现并不是很好，这是由于在对集成数目进行更新时，随着集成数目的改变，算法的运行时间会更长；并且在对基分类器分配不同权值之后，训练时也对算法的时间效率有影响。

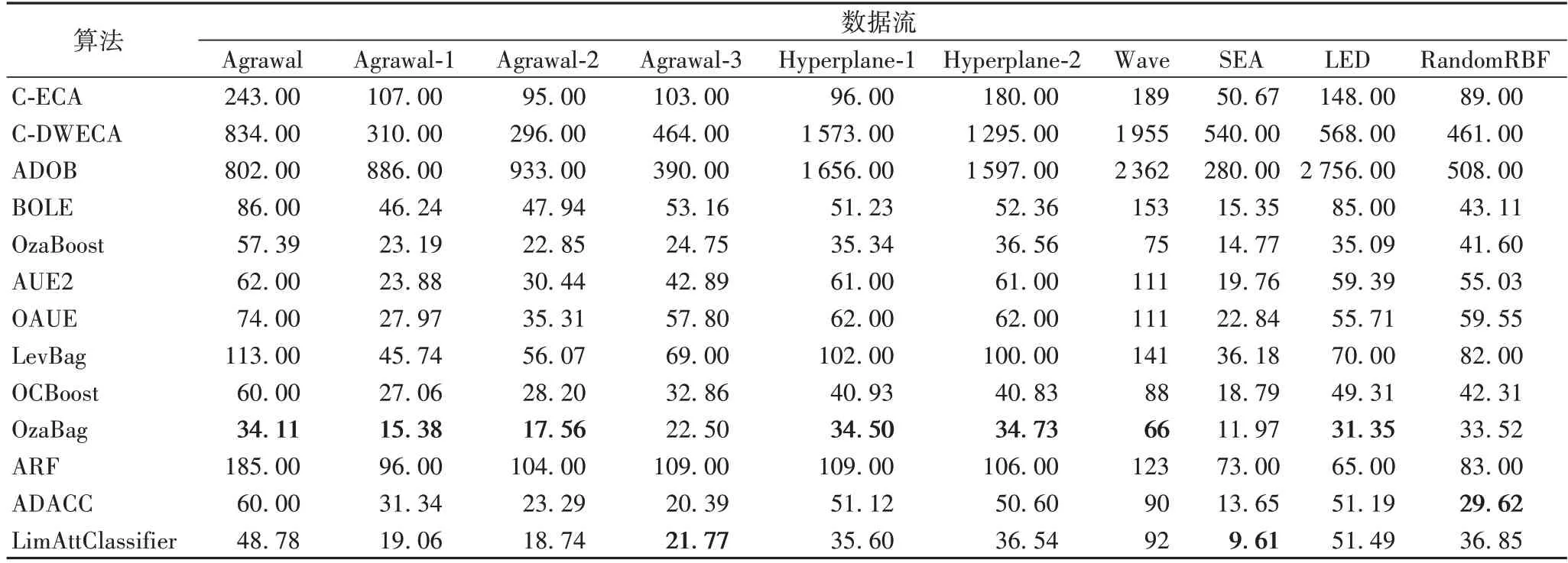
表5 C-ECA、C-DWECA与不同对比算法的时间效率对比 单位：sTab.5 Comparison of time efficiency between C-ECA，C-DWECA algorithms and different comparison algorithms unit：s

为了能更直观地观察实验结果的情况，通过图的形式对实验结果进行了展示。其中图7（a）～（d）分别展示了在Agrawal-2、Hyperplane、Hyperplane-1 以及SEA 数据流上生成树深度的大小，从图7（a）和图7（d）可以很直观地看出本文所提出的C-ECA 在生成树的深度上表现出了很优异的结果。

4 结语

随着数据流的复杂性日益增加，在现实生活中对集成分类算法的要求越来越严格。本文设计并研究了准确率爬坡集成分类算法（C-ECA）和基于爬坡的动态加权集成分类算法（C-DWECA），用于解决数据流问题。基于传统算法中集成数目设置为固定值的思想，C-ECA 依据准确率对集成数目进行更新。C-DWECA 是对C-ECA 的改进，通过加权函数w(x)来对基分类器的权值进行更新，为每个基分类器分配合适的权值，从而达到提高分类准确率的目的。通过实验结果表明，C-ECA 和C-DWECA 在分类准确率方面优于其他算法，C-DWECA 在RandomRBF 数据流上准确率更是达到了97.44%；但是，在时间效率方面，C-ECA 和C-DWECA 相对低一点，这是因为集成数目在相对多的时候，运行时间也相对久一点，并且权值的分配也会消耗一定的时间。在未来的工作中，将着重于提高改进算法的时间效率，在保证准确性的前提下，使算法的执行时间更短。