动态数据上的高效用模式挖掘综述

单芝慧，韩 萌，韩 强

（北方民族大学计算机科学与工程学院，银川 750021）

0 引言

频繁模式挖掘（Frequent Pattern Mining，FPM）旨在发现客户事务数据集中的频繁模式。1994 年Agrawal 等［1］第一次提出了频繁模式挖掘算法Apriori，但挖掘出的项集不能体现项的利润，会出现无意义的模式。为了解决频繁模式挖掘的限制，提出了高效用模式挖掘（High Utility Pattern Mining，HUPM）。效用挖掘是为了发现具有高效用的模式，为每个项设置内部效用和外部效用，以挖掘高利润的项集。若项集的效用大于或等于用户设置的最小效用阈值，该项集便被认为是具有高利润的即高效用的。Liu 等［2］提出了两阶段高效用项集挖掘（High Utility Itemset Minging，HUIM）算法。考虑到事务的长度对利润的影响，研究者进一步提出了高效用平均项集挖掘［3-4］。对于序列数据集，Yin 等［5］首次提出了高效用序列模式挖掘。由于用户通常很难界定阈值的大小，研究者进一步提出了在事务数据集中挖掘top-k个高效用模式［6］。

在移动计算方面应用高效用模式挖掘能够发现有趣的模式。高效用空间模式挖掘可以通过具有全球定位系统（Global Positioning System，GPS）服务的移动设备记录用户的移动日志，结合日志和支付记录，可以生成移动路径与购买事务的序列。例如，一个移动序列模式表示顾客经常通过路径在A 处吃火锅，在C 处购买果茶。若店主了解这种模式，就可以对在A 处吃过火锅的顾客促销果茶，提高顾客的购买欲望；投资者也可借助该模式判断是否在周边开设果茶店铺［7］。挖掘Web 访问序列可以从Web 日志中发现有用的知识，通过分析用户在网页中花费的时间，提取更真实的信息［8］。对生物基因序列应用高效用模式挖掘技术也可以发现有用的知识，同时考虑基因-疾病关联程度来提出效用模型，从时间进程微阵列数据集中发现重要的高效基因调控序列模式［9］。高效用模式挖掘在商业智能中有广泛的应用如购物篮分析。用户的购买行为包含有价值的信息，可以通过分析用户行为，挖掘具有高利润的购买行为。将用户购买数量定义为内部效用，物品利润定义为外部利润，从而进行挖掘操作［10］。使用“效用”衡量模式对用户的重要性，高效用模式挖掘还可以用于风险预测，如预测疫情期间哪个城市将会成为疫情暴发点，或预测微博、推特等社交媒体中下一阶段的热门话题。详细信息如图1 所示。

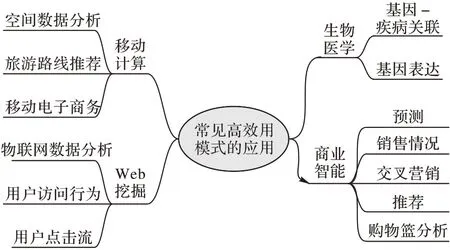
图1 常见高效用模式的应用Fig.1 Common applications of high utility pattern

在实际应用中事务数据集会插入新的事务，使得存储在数据集中的数据量不断增加。传统的高效用模式挖掘是以批处理模式运行的，若用户想要从更新的数据集中提取模式，需要从头开始挖掘，即它忽略了先前的结果，这种方式效率低下。近年来，已经提出了几种增量高效用项集挖掘（incremental High Utility Itemset Mining，iHUIM）算法［11-12］。开发高效的iHUIM 算法是一个新兴的研究，它使HUIM 任务在数据集更新方面具有更好的伸缩性。为了提高性能，还提出了基于树结构［13-14］和列表结构［15］的iHUIM 算法。在信息时代，数据都是作为流产生的，网站上的用户活动、金融交易等数据流包含与一般静态数据相似的信息，但其到达速度快、数量多，使得流中的数据只能挖掘检查一次，且尽快生成挖掘结果。目前已经提出了在滑动窗口（sliding window）［16］、衰减窗口（damped window）［17］、界标窗口（landmark window）［18］上挖掘高效用模式的技术。

Gan 等［19］对增量高效用模式挖掘算法进行了分类对比。Suvarna 等［20］从数据集的角度对静态数据及数据流上的高效用模式挖掘算法进行了总结。Fournier-Viger 等［21］对高效用模式挖掘算法进行了总结，主要是针对静态数据，仅有一小节涉及动态数据。王少峰等［22］对数据流上的高效用模式挖掘算法进行了总结比较。此前的文献大多从静态数据或仅从增量或者数据流中的一个方面介绍算法，并未对整个动态数据上的算法进行分类总结，而本文对不同类型的动态数据上的高效用模式挖掘算法进行了分类总结。本文的主要工作如下：

1）首次从动态数据的角度，即增量数据、数据流、动态删除和动态修改数据上对高效用模式及融合高效用模式进行了较全面的分析总结。

2）从树结构、列表结构和其他结构对高效用模式进行了分类总结，明确了不同结构上算法的特点。

3）从动态利润、动态序列和动态空间数据的角度对算法进行了总结。

1 概念与定义

本章介绍高效用模式的一些基本计算公式及定义，此外，还介绍了不同动态数据集的特点。

令I表示项i的集合，即I={i1，i2，…，im}是一组项，D={T1，T2，…，Tn}是事务数据集，其中每个事务Ti中的项是I的子集。项集X是I的子集。事务Tq中的项ip的数量由n(ip，Tq)表示。外部效用s(ip)是效用表中项ip的单位值（例如利润）。事务Tq中项ip的效用，由u(ip，Tq)表示，为内部效用与外部效用的乘积，定义为n(ip，Tq)×s(ip)。

定义1内部效用［23］。在事务T中项i的内部效用定义为in(i，T)。

例如：在表1 中，T2中项a的内部效用为in(a，T2)=1。

表1 事务数据集Tab.1 Transaction dataset

定义2外部效用［23］。项i的外部效用定义为ex(i)。

例如：在表2 中，项a的外部效用为ex(a)=5。

表2 效用表Tab.2 Utility table

定义3项的效用［23］。事务T中项i的效用定义为：

例如：在表1 中，事务T2中项a的效用为：

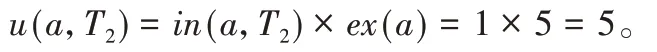
定义4项集的效用［23］。项集X为I的子集。事务Tq中X的效用，由u(X，Tq)表示，定义为：

例如：表1 中，在事务T2中项集{ab}的效用为u(ab，T2)=u(a，T2)+u(b，T2)=1× 5+2× 4=13。

定义5项集在数据集中的效用［23］。项集X在数据集中的效用，由u(X)表示，定义为：

例如：项集{ab}在数据集中的效用为

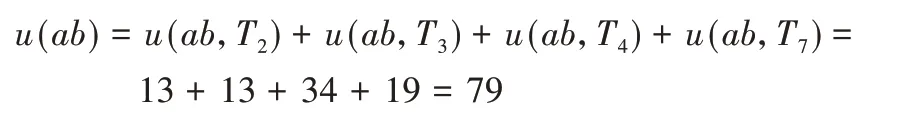
定义6最小效用阈值［23］。δ是用户指定的0-1 的数，最小效用阈值为：

定义7事务效用［23］。事务Tq的事务效用定义为：

定义8事务加权效用［23］。项集X的事务加权效用定义为twu(X)，是项集X包含的所有事务的效用之和：

定义9高事务加权效用项集［23］。对于项集X，如果twu(X) ≥mintuil，则X是高事务加权效用项集。

定义10 平均效用［3-4］。l(X)表示项集X的长度或大小，项集X在事务T中的平均效用定义为au(X，T)：

定义11高平均效用项集［3-4］。如果au(X) ≥minutil，X是高平均效用项集。

定义12最大效用［3-4］。事务T的最大效用标记为mu(T)，定义为：

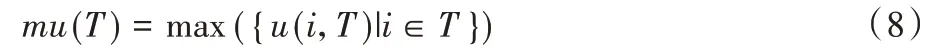
定义13平均效用上边界［3-4］。项集X的平均效用上界标记为ub(X)，定义为：

对于序列数据集，序列S的每个事件e中的每个项i都包含一个内部效用值intU(i，e，S)［5］。每个不同的项都有相应的外部效用程序值extU(i)。

在序列S的事件e中，项i的效用是utility(i，e，S)，是其内部效用和外部效用的乘积utility(i，e，S)=intU(i，e，S)×extU(i)。序列S中的模式P的效用为utility(P，S)，可以通过对该序列中出现的所有模式项的效用求和得出。n个序列的序列数据集SD中的模式P的效用［5］定义为：

例如表3 和表4，序列S2的事件2 中d的效用定义为：

表3 序列数据集Tab.3 Sequence dataset

表4 序列数据集的外部效用Tab.4 External utility of sequence dataset

utility(d，2，S2)=intU(d，2，S2)×extU(d)=2× 2=4，同理可得utility(b，3，S3)=9。

例如表3 和表4，序列S5中模式的效用为utility()=12+4=16。

事务中项的单位利润记为pu(i，T)，事务T中的项i的购买数量表示为qu(i，T)。项在事务中的效用表示为u(i，T)［24］得出u(i，T)=qu(i，T)×pu(i，T)。

例如，表5 描述的数据集［24］，事务T2中项b的单位利润为1.9，在T2中的购买数量为1，因此在T2中项b的效用为u(b，T2)=qu(b，T2)×pu(i，T2)=1.9× 1=1.9。项b在数据集中的效用计算为u(b，T1)+u(b，T2)+u(b，T4)+u(b，T5)=2+1.9+4+8=15.9。

表5 动态利润数据集Tab.5 Dynamic profit dataset

2 增量数据

数据的时间尺度决定了如何处理和存储数据。动态数据或事务数据定期更新信息，随着新信息的出现，它会随时间产生变化。现实世界的数据大多数是动态数据，随着时间的推移事务不断积累。本章总结了增量数据上的高效用模式挖掘算法。

2.1 基于树结构

使用树结构将效用信息存储在树节点上能够减少数据集扫描次数，减少内存的使用且能够更高效地挖掘高效用模式。目前，研究者已经提出了不同的树结构挖掘高效用模式，都具有较好的性能。本节总结了基于树结构的增量高效用模式挖掘算法，并对算法使用的剪枝策略、方法及优缺点等信息进行了总结。

Ahmed 等［25］第一次提出了在动态数据上挖掘高效用项集（High Utility Item，HUI）的算法，使用树结构IIUT（Incremental and Interactive Utility Tree），该数据结构具有构建一次数据结构执行多次挖掘操作的性能。它利用模式增长挖掘方法避免逐级生成候选和测试问题，与其他算法相比，仅需两次数据集扫描。它使用事务加权效用（Transaction Weighted Utilization，TWU）值作为剪枝策略减少搜索空间。IIUT 在头表和树的节点内显式维护TWU。为了促进树的遍历，还维护了相邻的链接。Ahmed 等［26］进一步提出了三种树结构来提高算法的性能，分别为IHUPL-Tree（IHUP Lexicographic Tree），IHUPTF-Tree（IHUP Transaction Frequency Tree），IHUPTWU-Tree（IHUP-Transaction-Weighted Utilization Tree）。前两者减少了内存，后者提高了挖掘效率。引入事务频率（Transaction Frequency，TF）提高第二次数据集扫描的速度，但该树结构IHUP-Tree 是冗余的，因此IHUP 算法的效率相对较低。Song 等［13］提出了一种并发算法CHUI-Mine（Concurrent High Utility Itemsets Mine），用于通过动态剪枝树结构来挖掘高效用项集。该算法引入CHUI-Tree树结构存储候选项集的效用信息，通过树构建过程中的高效用项集的计数变化实现树的剪枝。CHUI-Mine 算法利用并发策略，可以同时实现构建CHUI-Tree 和发现高效用项集，无需等待整棵树构建完成。

为了进一步优化数据结构，Zheng 等［14］提出了iCHUM（incremental Compressed High Utility Mining）算法。该算法利用项的TWU 来构造树结构iCHUM-Tree，将新增的数据附加到原始数据集后，iCHUM 算法将更新iCHUM-Tree，无需完全重建树结构。高效用项集的信息保留在iCHUM 树中，在头表中按照TWU 降序排序，自底向上有序遍历分支，提高挖掘效率。该算法使用模式增长方法挖掘，递归挖掘的复杂度由iCHUM-Tree 的高度和节点数确定。Yun 等［27］基于树结构HUPID-Tree（High Utility Patterns in Incremental Databases Tree）提出了 HUPID-Growth（High Utility Patterns in Incremental Databases Growth）算法。HUPID-Tree 只需要一次数据集扫描，为了更有效地处理增量数据创建了TIList（Tail-node Information List），使用HUPID-Growth 挖掘方法减少高估的效用，以此来减少搜索空间和候选项集的数量。

Kim 等［28］提出了IMHAUI（Incremental Mining of High Average-Utility Itemsets）算法用于在增量数据集上挖掘高平均效用项集。该算法提出了一个新的树结构IHAUI-Tree（Incremental High Average Utility Itemset Tree），采用了重组技术中的路径调整方法来构建更紧凑的树，基于AUUB（Average-Utility Upper-Bound）降序重构IHAUI-Tree。该算法使用模式增长方式来挖掘，减少了数据集扫描的次数及产生候选项集的数量，但是产生候选项集仍需消耗大量的时间。Radkar 等［29］提出了FUPT-HOUIN（Fast updated Utility Pattern Tree for High On-shelf Utility Items with Negative value）算法，用于从动态数据集中挖掘带有负项值高效用货架项集。该算法采用树结构，在第一阶段，扫描原始数据集构建效用树；在第二阶段更新效用树，必要时会重新扫描数据集，不是每次变化都扫描数据集。效用树避免了不必要的项集产生并减少了执行时间。Ahmed 等［30］提出了在Web 序列中挖掘高效用项集的方法，提出了新的树结构IUWAS-tree（Incremental Utility-based Web Access Sequence Tree）。该树结构只需要一次数据集扫描即可构建并挖掘所有的候选序列，使用Web 访问序列效用（Web access sequence utility，wasu）来剪枝搜索空间，该算法使用序列模式增长挖掘方法避免逐级生成候选、验证和多次数据集扫描问题。Wang等［31］提出了IncUSP-Miner（Incremental Utility Sequential Patterns Miner）算法在增量数据上挖掘高效用序列模式（High Utility Sequential Pattern，HUSP）。该算法提出了一个更严格的序列效用上边界（Tight Sequence Utility，TSU）来避免冗余计算；此外，还设计了新的候选模式树来维护TSU 值大于或等于最小效用阈值的序列，将一组辅助效用信息存储在每个节点中，并且无需重新计算就可以快速获得该序列的辅助信息，从而提高了挖掘效率。Wang 等［32］进一步提出了IncUSP-Miner+算法来逐步挖掘HUSP。该算法提出了一个更严格TSU，并且设计了紧凑的候选模式树，以缓冲其序列TSU 值大于或等于原始数据集中的最小效用阈值；使用节点跳过策略来提高挖掘效率，对于不能跳过的节点，使用了两个策略来减少数据集扫描的规模。为了更清晰地比较各个算法的区别，本文对动态数据集上使用树结构的高效用模式挖掘算法进行总结，如图2 所示。

图2 基于树结构的HUPM算法Fig.2 Tree structure-based HUPM algorithms

2.2 基于列表结构

效用列表通常会存储项的标识符、效用及剩余效用，并按照TWU 大小排列，随着事务的插入，TWU 与剩余效用将会不断变化。效用列表结构占用的内存相较于原始数据集非常小，能够有效减少内存，且列表结构无需产生候选项集。本节对使用列表结构的高效用模式挖掘算法进行了总结。

Lin 等［15］提出了HUI-list-INS（High Utiltity Itemsets list INSertion）算法。该算法使用列表结构减少计算消耗，且不产生候选项集，使用枚举树和2-项集之间的关系提高计算速度，使用项集的内部效用与剩余效用之和作为剪枝策略，减小了搜索空间。另外，在该算法中还采用了估计效用共现（Estimated Utility Co-occurrence，EUCP）修剪策略，以进一步保持2-项集的关系，从而消除了效用较低的扩展项集。Yun等［33］提出的LIHUP（List based Incremental High Utiltiy Pattern）也使用效用列表存储效用信息，仅需扫描数据集一次，无需产生候选项集，通过扫描原始数据集来构建全局列表，利用ru（remain utiltiy）来重建全局列表。Kim 等［34］提出了LIMHAUP（List based Incremental Mining of High Average Utility Pattern），使用HAUP-List（High Average Utility Pattern List）更紧凑地存储模式信息，并设计了一个重组过程来处理新插入的数据。

Yun 等［35］提出了基于索引列表的IIHUM（Indexed list based Incremental High Utility pattern Mining）算法，仅需要一次数据集扫描。数据集的信息被存储在IIU-List（Incremental Indexed Utility List）中，列表存储了NextItem，NextItem 指向相应事务中当前项旁边的项标签；ActUtil（Actual Utility）是事务中当前项的实际效用值；NextIdx 指示IIU 列表中与当前项所在的下一个项相对应的条目；SumUtil（Sum of the ActUtil）是当前IIU 列表中所有ActUtil 值的总和；RUtil 表示当前项扩展到最大值时可以添加到SumUtil 的最大效用值。该算法通过TWU 升序重组全局IIU-List，以更有效的方式从增量数据中挖掘高效用模式，将模式P的上边界设置为效用与剩余效用之和。Dam 等［36］提出了IncCHUI（Incremental Closed High-Utility Itemset miner）算法，该算法可从增量数据中有效地挖掘闭合高效用项集（Closed High Utility Itemsets，CHUI）。该算法使用增量式效用列表结构，根据最佳排序顺序对列表进行重组，使用TWU 快速构造增量效用列表，并消除未更新的候选对象。最后该算法提出一种有效的基于散列的方法来更新或插入找到的新闭合项集。吴倩等［37］提出了挖掘top-k高效用模式算法TOPK-HUP-INS（INcremental Top-KHigh Utility Pattern mining），使用效用列表存储事务信息。该算法需要两次数据集扫描来构建所有的1 项集，并使用深度优先扩展策略使得topkUti 快速增长，删除了大量低效用模式。Lin 等［38］提出了PRE-HAUIMI（Incremental updating the High Average-Utility Itemset Mining with PRE-large concept）算法在动态数据上挖掘高平均效用项集，该算法使用效用列表结构AUL（Average-Utility-List）并应 用HAUIM（High Average-Utility Itemset Mining）的预大（Pre-Large）概念加快挖掘性能，减少了重复的数据集扫描并获得了正确的HAUI（High Average-Utility Itemset）。此外，建立了枚举树来确定是否应探索树节点的超集，减少了对没有希望的候选项集的AUL 结构执行的连接操作。

张春砚等［39］提出了CIHUM（Compact Incremental High Utility Mining）算法，采用紧凑的效用列表CUL（Compact Utility List）和HUI-trie（High Utility Itemset trie）从增量数据集中挖掘高效用模式。HUI-trie 可以及时更新和存储高效用项集的效用信息。Nguyen 等［40］提出了CHUI-Mine（Closed High Utiltiy Itemset Mine）算法的优化版本，直接从动态利润数据中挖掘MHUI（Maximal High Utility Itemsets），使 用EUCS（Estimated Utility Co-occurrence Structure）和EUCP 剪枝技术减少候选项集。该算法还进一步使用了CUIP（Continuous Unpromising Item Pruning）来减少搜索空间中的候选项集和MHUIs 的挖掘时间。CUIP 通 过FUCS（First Utility Cooccurrence Structure）不断更新项的TWU 值。Nguyen 等［40］将P-set、EUCS 和EUCP、FCUS 和CUIP 合并到了CHUI-Power 算法的最终版本中，获得了较好的性能。Ishita 等［41］认为现有的算法并未考虑模式的规律性，故提出了在增量序列数据上挖掘规律的高效用序列模式的算法RIncHusp（Regular High utility sequential pattern mining in Incremental databases），使用列表结构来存储信息包括HS（High utility Sequences）和SHS（Semi-High utility Sequences）列表，并使用模式的效用和剩余效用来剪枝搜索空间。如果模式P的效用大于或等于最大剩余效用，将作为规则的半高效用序列存储在SHS 中；否则将被剪枝。效用列表的算法总结如图3 所示。

图3 基于效用列表的HUPM算法Fig.3 Utility list-based HUPM algorithms

2.3 其他数据结构

除了使用树与列表结构存储效用信息，仍然存在使用预大（Pre-Large）概念、两阶段等方式存储效用信息的算法。本节对这些算法进行了总结。

Hong 等［42］提出了一种两阶段算法在增量数据上挖掘高平均效用项集。在第一阶段，使用平均效用上边界高估项集，在第二阶段，计算高平均效用项集上边界的实际平均效用值；但其运行时间和内存消耗等性能较低。Lin 等［43］提出了FUP-HUI（Fast UPdate High Utility Itemset），该算法根据项集是否属于原始数据集以及新数据集中的高TWU 项集将它们划分为四个部分，然后处理每个部分，以自己的方式更新发现的高效用项集。Lin 等［44］进一步提出了FUP-HU（Fast UPdate High Utility），该算法比两阶段批量挖掘算法具有更好的性能；但是，如果某些项集在原始数据集中较小，而在新插入的事务中较大，则仍需要重新扫描数据集，耗费时间。

Lin 等［45］提出了PRE-HUIDE 的两阶段算法以有效地维护基于预大概念发现的高效用项集。该算法结合且修改了两阶段算法和预大概念。项集首先分为三个部分，然后对每部分执行单独的操作，定义了上边界和下边界来区分高（大）和预大效用项集。预大概念用于通过确定新插入的事务数来减少对原始数据集的重新扫描，仅当插入的事务数大于安全范围时才需要重新扫描原始数据集，使用向下闭包属性减少候选项集的数量和扫描数据集的时间。但以上算法仍然需要额外的数据集扫描且产生了大量的候选项集。为了解决以上问题，Lee 等［46］提出了一个更高效的基于Pre-large 概念的PIHUP（Pre-large Incremental High Utility Patterns）算法，提出了更适用Pre-large 概念构造树来存储和维护数据，使用两个阈值Su和Sl，有效地减少了冗余操作和内存空间，但该算法使用了高估原则来保证向下闭包属性，产生了无用的候选模式。Nguyen 等［24］提出了在动态利润数据上挖掘高效用项集的算法MEFIM（Modified EFficient high-utility Itemset Mining），重新定义了效用度量，还提出了MEFIM 算法的改进版 本 iMEFIM（incremental Modified EFficient high-utility Itemset Mining）。iMEFIM 引入了 一种称 为P-set（TIDs（Transactions IDs）Projection of an itemset on a database）的新颖数据结构，事务标识符（TID）在数据集上投影项集的概念可用于减少在投影数据库中需要确定哪些项可以附加到项集，以生成潜在的高效用项集进行扫描的事务数量，使用事务合并以及局部效用和子树效用上限来修剪搜索空间。

空间数据挖掘［47］可以用来从空间数据中发现有趣的和未知的模式，空间共处同一位置表示一组经常在附近区域观察到的空间特征，其应用包括：生物种群，如西尼罗河病毒，它经常出现在蚊子多的地区；交通问题，如交通拥堵与车祸之间的关系。Wang 等［48］提出了在增量空间数据集中挖掘空间高效用的基本算法，但是不够高效，进而提出了PUCP（Part Update of Co-location Patterns）算法更高效地更新高效用共处模式。更新空间模式是一个复杂的过程，因为新数据会增加新的邻居关系，该算法只计算新变换的邻居关系的值，邻居数量的增加可能会影响到高效用协同托管挖掘的结果。Wang 等［49］提出了UUOC（Utility Update Of Co-locations）算法，该算法解决了当空间数据集通过增加和减少数据点而不断变化时进行增量式高效用协同定位挖掘的问题，使用变化的共置位实例有效地更新已经变化的共置位模式的效用值，只需要处理变化后的模式。该算法将更改后的共处位置分为四种情况，并利用变更后的共处位置的性质和引理来减少UUOC 的计算成本。

2.4 算法性能评估

为了更清晰地观察算法的性能，本文采用定量分析的方法对同一数据集上的不同算法的运行时间和内存消耗进行了对比。此外，还对部分增量数据上的高效用模式挖掘算法的时间复杂度进行了分析比较。

本文选取了密集数据集Chess、Accident 和稀疏数据集Retail 比较算法的性能。在Chess 数据集上，CHUI-Mine 算法［13］在最小效用阈值为0.62 时，运行时间为580 s 左右，而两阶段算法的运行时间高于8 000 s，CHUI-Mine 使用了基于树的修剪策略，减少了候选项集的数量。CIHUM［39］在相同的条件下，运行时间比CHUI-Mine 更少，原因在于该算法使用效用列表结构。在Retail 数据集上LIHUP［33］优于HUPIDGrowth［27］，IIHUM 优 于LIHUP。HUPID-Growth 使用了树结构，很难具有节点共享的结果，故随着数据量的增大需要更多的内存。而LIHUP 使用列表结构，消耗的内存较少。随着数据量的增大，IIHUP 也表现出了较稳定的运行时间的增加。IIHUM 算法在稀疏数据集上优于HUPID-Growth 与LIHUP。HUPID-Growth 在相对较小的数据集上有较好的性能，但是随着最小效用阈值的降低，HUPID-Growth 算法的运行时间急剧增加，在Accident 数据集上当最小效用阈值由30%变为20%时，HUPID、LIHUP 比IIHUP 的运行时间分别增加了44.49%、4.49%和1.5%。HUPID-Growth 算法运行时间剧增的主要原因是需要构造大量的本地树结构并且产生了许多候选项集，而IIHUP 使用了更有效的列表结构无需产生候选项集。此时的内存消耗也在增加，但是增加速度较为缓慢。IIHUP 在稀疏数据集及密集数据集上的性能都要优于其他两种算法。

算法的时间复杂度和空间复杂度表明了算法的性能。iCHUM算法［14］构建iCHUM-Tree的空间复杂度为O()，其中mp表示有希望的项数；更新的时间复杂度为O()，其中n表示事务数，在最坏的情况下，它需要对mp个条目进行n次冒泡排序。挖掘iCHUM-Tree的时间复杂度为O()，其中h是iCHUM-Tree的高度，mp表示有希望的项数。HUPID-Growth算法［27］的时间复杂度由树的构造、重构树以及挖掘过程三部分组成。令No和Ni分别为原始数据集和从原始数据集递增的数据集中的事务数，Nm为数据集最长事务中的项数，需要O((No+Ni)×(Ni+1))的执行时间，将原始数据集中的事务和增量增加的数据集插入到树中。算法花费O(No×(Nm+2))的执行时间通过提取、排序和重新插入所有路径来重构树，再次重组树需要O((No+Ni)×(Nm+2))的时间，挖掘过程的复杂度O(No×(Nm+1))。算法总的时间复杂度为

对于IMHAUI 算法［28］，设n为增量数据集中包含的不同的项数，l为从数据集生成的项集的最大长度。该算法在整个增量挖掘过程中扫描数据集的时间复杂度为O(n2+n)，即O(3n2)。计算候选项的实际平均效用需要O((l+1)×n)的执行时间。在挖掘过程中对AUUB 降序重构的时间复杂度最坏情况为O(n2)。在IHAUI-Tree 中为n个项构造局部树需要O(2×m×n)的时间复杂度。整个挖掘过程的时间复杂度为。由于随着递归模式增长操作的深度增加，本地树的递归模式增长操作的时间逐渐变少，因此整个挖掘过程的时间复杂度可以简化为O(n2)。

在LIHUP［33］中令No和Ni为分别由Nm个项组成的原始数据集和增加的数据集中的事务数，Nc为候选项数。该算法用于增加的数据集的时间复杂度相较于原始数据集为O(No×Nm×Nc) 或O((No+Ni)×Nm×Nc)。LIMHAUP 算法［34］中，令事务数为m，项的个数为n，读取数据集并构建HAUP-List 需要O(m×n)，对HAUP-List 排序需要O(nlbn)，重构HAUP-Lists 的复杂度为O(m×n)，重构步骤总的时间复杂度表示为O(t×(nlbn+m×n))，t表示相同数据集插入的次数，挖掘过程的复杂度为O((2n-n)×m)。LIMHAUP 算法的总复杂度为O(m×n+t×(nlbn+m×n)+(2n-n)×m)。IncCHUI 算法［36］的时间复杂度由全局数据结构的构建和更新与模式搜索组成。令nd与nn分别为原始数据集与增加部分的事务数，w为平均事务长度，m为不同的项的数目。全局数据结构构建和更新的时间复杂度为O(nd×w+2 lg(m)+m×w)或者为O(nn×w+2mlg(m)+m×w)，分别大致为O((nd+m)×w)或O((nn+m)×w)，因为排序只执行一次。搜索过程的时间复杂度为O(2m-1)。PRE-HAUIMI算法［38］中，设n是数据集中的事务数，数据集中最大事务的项数是m，因此在最坏的情况下，第一次数据集扫描需要O(m×n)的时间。计算数据集中事务效用总和需要O(n)，在最坏情况下建立AUL 结构需要O(m)。设原始数据集中每个案例有k个项集，简单的操作将两个AUL 结构连接操作需要O(k×N)的时间，其中N是维护案例数。PRE-HAUIMI 算法中AUL 结构的维护部分最多计算为O(m×n+n+m+k×N)。根据以上4 个基于效用列表的算法可以看出其根本区别在于构造数据结构与挖掘过程的复杂度。此外，不同挖掘不同的模式，其搜索过程的复杂度也大不相同，可从高平均效用项集挖掘算法LIMHAUP 与闭合高效用模式挖掘算法IncCHUI 挖掘过程的复杂度看出。

3 数据流

大部分研究高效用模式挖掘的算法都集中在静态数据集上。随着新应用的出现，处理的数据可能在连续的数据流中，例如网络流量分析、网络入侵检测和在线分析。数据流不仅连续、速度高而且不受限制，因此流中的每个项只能检查一次，并需要尽快地生成挖掘结果。传统的高效用模式挖掘需要多次扫描数据集，不适用于处理数据流上的数据。数据流上的高效用模式挖掘已经成为一个重要的研究主题。本章按照在数据流上HUIM 所使用的不同类型的滑动窗口来描述算法，如滑动窗口（sliding window）［16］、衰减窗 口（damped window）［17］和界标窗口（landmark window）［18］。

3.1 滑动窗口模式的高效用算法

滑动窗口并未明确定义窗口的起始与结束位置，仅定义了窗口的大小N。令Tnew表示新事物，Tnew-N+1表示历史事务，即算法处理Tnew-N+1和Tnew之间的最新事务数据。当Tnew+1到达时，Tnew-N+1会被移出窗口。处在窗口内的事务具有相同的重要性，窗口以固定大小在数据流上进行滑动，不断输出结果。数据流挖掘使用较多的窗口模型便是滑动窗口模型（Sliding Window Model，SWM）［50］。

Tsai［16］提出了一种基于加权滑动窗口模型的HUIM 一阶段算法HUI_W，使用TWU 减少搜索空间，重复使用存储的信息，从而可以有效地发现数据流中所有的高加权效用项集；但该算法产生了大量错误的候选项集，消耗了大量的内存。Chu 等［51］提出了第一个从数据流中挖掘临时高效用模式的算法THUI（Temporal High Utility Itemset）-Mine。该算法是两阶段算法，使用滑动窗口过滤技术。该算法在每个分区中采用过滤阈值来处理生成的事务加权效用项集（Transaction Weighted Utilization Itemsets，TWUI）。Li 等［52］提出了两种一阶段算法MHUI-BIT（Mining High Utility Itemsets based on BITvector）和MHUI-TID（Mining High Utility Itemsets based on TIDlist）从事务敏感的滑动窗口中挖掘高效用模式。该算法利用事务加权效用的向下闭包属性，并使用位向量和TIDlist存储项的信息，构造字典树挖掘HUI，有效减少了候选项的数量、处理时间和内存使用，优于THUI-Mine。Li 等［53］进一步提出在数据流上挖掘带有和不带负效用的高效用模式，使用相同的数据结构提高算法的效率。字典树结构只存储候选2 项集，每个项的信息都能够在当前的窗口中获得且不需要重复扫描，但逐级生成候选模式方法，使得算法在时间和存储效率方面性能较低。

Li 等［54］提出了MHUI-max，使用TID 列表和基于字典树的数据结构LexTree-maxHTU 存储来自当前事务敏感滑动窗口中的最大高效用模式，产生了较少的候选项集。与MHUIBIT 相比，该算法在最后一阶段产生的候选项集所需内存较少。以上算法都不具有一次构建多次挖掘（Build Once Mine Many）［55］的特性。Ahmed 等［55］提出了使用HUS-tree（High Utility Stream tree）的HUPMS（High Utility Pattern Mining over Stream data）算法进行增量式和交互式HUPM。该算法使用模式增长方式减少了大量的候选项集。此外，HUS-tree 的一次构建挖掘多次的性能对交互式挖掘非常有效，减少了内存的消耗。Shie 等［56］提出了GUIDE（Generation of maximal high Utility Itemsets from Data strEams）框架，从数据流中挖掘最大高效用模式，使用基于时间敏感的滑动窗口GUIDESW算法，利用MUIsw-Tree 维护效用信息，是一种一阶段算法，且使用事务投影技术，并对事务进行排序以更新树结构。Feng等［57］提出了HUM-UT（High Utility itemsets Mining based on UT-Tree）算法，使用滑动窗口过滤方法UT-Tree（Utility on Tail Tree）来维护项集的效用信息，效用信息仅存储在尾节点上。HUM-UT 算法仅需一次数据集扫描，且不产生候选项集。

Zihayat 等［58］提出了T-HUDS 算法在数据流的滑动窗口上挖掘top-k的高效用模式，使用更紧凑的树结构HUDS-tree存储事务信息。T-HUDS 使用前缀效用模型剪枝搜索空间，产生了较少的候选项集，使用模式增长的方式有效地剪枝搜索空间。该算法提出了几种初始化和动态调整最小效用阈值的策略，但是该算法是两阶段算法，耗费时间。慕欢欢等［59］提出了HUIDE（High-Utility Itemsets over Data Streams）算法，提出了一种有效的效用度量方法，采用基于时间的滑动窗口技术并构建HUI-tree（High Utility Itemsets tree）来存储效用信息。该算法仅需一次数据集扫描，减少了候选项集的数量和时间、空间的消耗。Ryang 等［60］提出了SHU-Growth（Sliding window based High Utility Growth）算法，该算法基于HUPMS 提出了SHU-Tree（Sliding window based High Utility Tree）结构，提出了通过减少高估的效用来减少搜索空间和候选项集的技术RGE（Reducing Global Estimated utilities）和RLE（Reducing Local Estimated utilities），通过减少高估的效用强调最新数据，并应用滑动窗口模型有效地挖掘。Yun等［61］提出了SHUPM（Sliding window based High Utility Pattern Mining）算法和列表结构SHUP-List（Sliding window based High Utility Pattern List）用于在滑动窗口模式的基础上找到数据流上的高效用模式，使用SHUP-List 无需产生候选项集，并使用psum 来剪枝搜索空间。谢志轩等［62］提出了IHUM-UT（Improved High Utility Mining based on Utility Tree）算法。该算法使用全局头表Global_HT 和全局树UT-Tree 来存储效用信息。Jaysawal 等［63］提出了一阶段算法SOHUPDS（Single-pass One-phase algorithm for mining High Utility Patterns over a Data Stream），使用了投影数据库方法和滑动窗口技术；此外，还使用IUDataListSW 作为数据结构，存储了当前滑动窗口中各项的效用和上边界。IUDataListSW 存储项在事务中的位置，有效地初始投影数据库并使用局部效用剪枝搜索空间。为了更有效地发现高效用模式，设置了两个布尔值将节点分为了四种情况，能够有效地更新当前滑动窗口中的高效用模式。基于滑动窗口的高效用模式算法如表6 所示。

表6 基于滑动窗口的高效用模式算法Tab.6 Sliding window-based high utility pattern algorithms

数据流上高效用模式挖掘算法的性能比较实验包括运行时间、内存消耗和可扩展性等。其中每个性能需要进行的实验包括不同最小效用阈值下的实验，不同窗口大小下进行的实验，在同一窗口下包含的批事务数也存在不同情况，以上情况均反映着算法的性能。由于目前数据流上的高效用模式挖掘算法不多，本文以3 个较新的算法为例，对其在Chainstore 数据集［63］上，在窗口大小为6 的条件下进行对比。HUPMS［55］的执行时间超过2 500 s，SOHUPDS［63］的执行时间在100 s 之内，SHUPM［61］的运行时间介于两者之间。其内存使用情况也是如此，SOHUPDS 内存消耗少于SHUPM，SHUPM 少于HUPMS。HUPMS 使用了树结构，SHUPM 使用了列表结构，可见列表结构的性能优于树结构的性能，数据库投影方法对算法的性能有更明显的提升，SOHUPDS 使用了数据库投影的方法，使用IUDataListSW 存储当前窗口的效用和项的上界，还存储了项在事务中的位置，能够有效地获取有希望的项，进行下一步的扩展。随着窗口数目的增大，算法的执行时间及内存消耗也会不断增加。

3.2 其他窗口模式的高效用算法

窗口模式还有衰减窗口与界标窗口。此外，高效用模式挖掘仅考虑了项的数量和单位利润，为了使高效用模式挖掘算法进一步适用于现实生活场景，研究者进一步提出了数据流上的高效用序列模式、平均高效用模式和top-k高效用模式等算法。本节总结了使用其他窗口模式在数据流上挖掘融合高效用模式的算法。

Shie 等［56］提出了GUIDE 框架，从数据流中挖掘最大高效用模式，提出了基于衰减窗口的GUIDETF算法。该算法使用MUITF-Tree 维护效用信息，使用事务投影技术，并对事务进行排序以更新树结构，是一阶段算法。Manike 等［64］提出了使用时间衰减窗口在不确定数据流上挖掘高效用模式的算法，该算法使用树结构LHUI-Tree（Landmark window High Utility Itemset Tree）和SHUI-Tree（Sliding window High Utility Itemset Tree），该算法在时间和内存消耗方法有较好的性能，但仍可进一步提升。Kim 等［65］提出了基于树的算法GENHUI（GENerate recent High Utility Itemsets）挖掘最近的高效用项集RHUIs（Recent High Utility Itemsets），通过时间衰减模型，根据事务的到达时间来逐渐减少事务的效用。此外，该算法定期更新树结构RHUI-Tree 中的效用信息，用DTWU（Decayed TWU）作为高估的效用值，减小搜索空间。Yun等［17］提出了在数据流中挖掘高平均效用项集的算法MPM（Mining significance utility Pattern information from streaM data）。该算法基于时间衰减窗口，提出了新的数据结构DAT（Damped Average utility Tree）和TUL（Transaction Utility List）来存储效用信息，为了减少搜索空间使用dub（damped average utility upper-bound）作为剪枝策略。Nam 等［66］提出了一种基于索引列表DUI list（Damped Utility Indexed list）的算法ILDHUP（Indexed List Damped High Utility Pattern mining），从时间敏感的数据流来挖掘最近高效用模式，使用索引值快速搜索效用信息。该算法只需扫描数据集一次，使用dub 作为模式的上边界，该算法在连续存储新数据的环境中考虑插入数据的到达时间来挖掘最近的高效用模式。

Yun 等［67］提出了SHAU（Sliding window based High Average Utility pattern mining）算法来挖掘数据流上最近出现的高平均效用模式，基于滑动窗口模型，将流数据分为多个批次，并且仅将最近的批次保留在窗口中。该算法使用

SHAU-Tree（Sliding window based High Average Utility pattern Tree）存储最近流数据中的效用信息，并提出RUG（Reducing average utility Upper bound in the Global）策略最小化平均效用上界，减少产生候选项的数目，但算法的内存占用和运行时间仍可进一步减少。Lu 等［68］提出了基于滑动窗口的top-k的HUI 挖掘算法TOPK-SW（Top-KHUIs mining based on Sliding Window）。将事务项集和有效信息存储在树结构HUI-Tree（High Utility Itemsets Tree）中，确保有效检索效用值而无需重新扫描数据集，且无需生成候选项集。Dawar等［69］提出了从数据流中挖掘top-k高效用模式的一阶段的算法Vert_top-k_DS。该算法使用iList（inverted-List）作为数据结构，iList 的构建需要扫描数据集两次，第二次数据集扫描需要按照TWU 递增排序，该算法无需生成候选项集。Zihayat 等［70］提出了HUSP-Stream（High Utility Sequential Pattern Stream）算法挖掘高效用序列模式。该算法使用树结构HUSP-Tree（High Utility Sequential Pattern Tree）和效用列表ItemUtilLists（Item UtiityLists）来维护HUSP 的基本信息，使用TSWU（Transaction based Sequence-Weighted Utility）与SFU（Sequence-suFfix Utility）来剪枝搜索空间。Hackman等［71］提出了在数据流上挖掘短暂出现的高效用模式，定义了NHUI（Nearest High Utility Itemset），利用经过验证的预测模型来评估即将出现的高效用模式，该功能具有捕获和存储潜在高效用项集信息的能力。Tang 等［72］提出了一种基于树的数据流的高效用序列项集挖掘算法HUSP-UT（mining HUSPs based UT-tree）。该算法使用UT-tree 作为数据结构，使用普通节点、尾节点以及尾指针表存储事务的效用，能够快速计算项中的效用和新的swu（Sequential Utility of the current Window of the data stream）值，减少了运行时间。该树结构能够保证算法不产生候选项集，有效减少了内存的消耗。程浩东等［73］提出了在数据流上挖掘闭合高效用模式的算 法 CHUI_DS（sliding-window-model-based Closed High Utility Itemsets mining on Data Stream）。该算法使用效用列表结构CH-List，快速地执行批次的插入和删除，利用滑动窗口技术在有限的内存资源下从连续数据中发现最新的无冗余项集。该算法不产生候选项集，此外，还提出了基于BRU_table（Batch based Remaining Utility Table）的公共批次事务重组方法和减少闭包计算的剪枝技术，减少搜索空间。Shie 等［56］提出了GUIDELM（Generation of maximal high Utility Itemsets from Data strEams）框架，从数据流中挖掘最大高效用模式，使用MUILM-Tree 维护效用信息，是一阶段算法。Manike 等［74］在GUIDELM的基础上提出了MGUIDELM算法。该算法使用MMUI-Tree，提出的算法比其他算法产生的候选项集少。Zihayat 等［18］提出了MAHUSP（Memory Adaptive High Utility Sequential Pattern mining over data streams）算法，采用内存自适应机制使用内存，以便有效地发现数据流上的HUSP。该算法提出了一种紧凑的数据结构MAS-Tree，并运用界标窗口技术在数据流上存储潜在的HUSP；此外，该算法还提出了两种有效的内存自适应机制LBMA（Leaf Based Memory Adaptation）和 SBMA（Sub-tree Based Memory Adaptation）来处理可用内存不足以向MAS-Tree 添加新的潜在HUSP 的情况。基于窗口模式的高效用模式挖掘算法总结如表7 所示。

表7 基于窗口模式的HUPM算法Tab.7 HUPM algorithms based on window pattern

在MPM［17］中，数据结构DAT 的时间复杂度由以下部分组成：令给定数据集中的事务数为T，事务的平均长度为L，构造DAT 的时间复杂度为O(T×L)，更新节点的平均效用的时间复杂度为O(T×L)。在包含I项的头表中提取项的条件模式基的时间复杂度为O(I×L)。然后构造条件树，在最坏的情况下是所有的项都满足剪枝条件，保留条件树中的项。使用RI表示具有I项的树的递归模式增长操作的时间复杂度，RI为O(I×T+RI-1)，因此递归挖掘过程的总时间复杂度为。计算挖掘出的候选者数C的实际平均效用花费的时间复杂度为O(C×T)。在最坏的情况下，构建DAT总的时间复杂度。

MPM 的空间复杂度表示如下，主要的树结构DAT 由头表和前缀树组成，表包含两个类型的数据，Item 与该项的dub；树有多个节点，每个节点存储了项标签、支持度和dub。设K为数据集中不同项的数量，在最坏的情况下，构建DAT的空间成本为O(2×K+3×T×L)。若K为最大值，代价可表示为O(2×T×L+3×T×L)=O(5×T×L)。令C为DAT 生成的条件树中的节点数，D为条件树中不同项的数量，条件树的空间成本表示为O(2×D+3×C)。令O(R)为生成的所有可能条件树的空间成本，然后总空间复杂度表示为O(5×T×L+R)，其中最高阶项为T×L。因此，最终结果变为O(5×T×L)。

4 动态删除和动态修改数据方面的高效用算法

除了增量数据和数据流上的高效用模式挖掘算法，仍然有动态删除和动态修改数据方面的高效用模式挖掘算法。本章对该数据类型上的算法进行了总结。

4.1 动态删除数据

目前已经有不少算法在增量数据上挖掘高效用模式，但是，事务删除在实际应用中也是常见的。研究者已经提出了在动态删除事务数据集中挖掘高效用模式的算法。

Lin 等［75］提出了在动态删除的事务数据集中挖掘高效用项集的算法FUP-HUI-DEL（Fast UPdated High Utility Itemsets for transaction DELetion），使用两阶段算法和FUP（Fast UPdated）概念减少了候选项集的数量和数据集扫描次数，使用TWU 和项集的真实效用来减少候选项集的数量。Lin等［76］提出了PRE-HUI-DEL（PRE-large High Utiltiy Itemsets for transaction DELetion）算法，使用事务删除的预大概念挖掘高效用项集。该算法根据TWU 项集在原始数据集和已删除的事务中是否具有较大（高）、预大型或较小的事务加权利用率，使用预大的概念将事务加权的利用率项集划分为三组（有9 种情况）；然后将特定过程应用于每种情况，以维护和更新发现的高效用项集；定义上边界效用和下边界效用得出高（大）事务和预大事务加权效用的有效阈值，减少了数据集扫描次数，只存储了少数极有可能的项集，减少了内存的使用。

以上两种算法都为两阶段算法，且两种算法都需要进行大量计算，此外还需要多次扫描数据集确定项集的实际效用。Lin 等［77］提出了HUI-list-DEL 算法，使用效用列表结构，并使用项集的效用与剩余效用之和与EUCP 剪枝搜索空间。该算法避免了多次数据集扫描并且重新使用效用列表结构。Lin 等［78］提出了FUP-HAUIMD 挖掘高平均效用项集。该算法无需一直扫描数据集即可轻易找到更新的HAUIs，使用平均效用列表（AU-List）存储必要的分支用于之后的挖掘操作保证正确性和挖掘信息的完整性。Yun 等［79］提出了HUIPRED 算法。该算法使用树结构HUIPREDL-tree 并且应用了预大概念，能够更有效地分析动态数据集，提出的数据结构和两个阈值有效减少了数据集扫描的次数。

4.2 动态修改数据

现实生活中事务修改也是常见操作，在将收集的数据输入到数据集中时，可能会出现错误，致使一些信息变得无效或者加入了新的信息［80］。因此有效地维护事务修改是一个关键问题，本节总结了事务修改的高效用模式挖掘算法。

Lin 等［80］提出了基于预大策略来维护和更新已发现的HUIM 以处理事务修改，当事务修改时，该算法将发现的HTWUI（High Transaction Weight Utiltiy Itemsets）分为三个部分，设计了一个安全范围来减少事务修改时数据集重新扫描的计算量。Lin 等［81］提出了PRE-HUI-MOD（PRE-large-based HUIs for ransaction MODification）算法。当原始数据集进行修改时，将发现的信息分为3 个部分9 种情况，同样设置了安全范围可以大大减少多次数据集扫描的计算量方法。使用生成和测试机制的两阶段算法逐级挖掘HUI，需要额外的内存。Lin 等［82］提出了FUP-HUP-tree-MOD（Fast UPdated High Utility Pattern tree for transaction MODification）算 法，使 用HUP tree 结构来保存效用信息，减少了数据集重新扫描的计算。当原始数据集修改了事务时，算法将发现的高事务加权效用1 项集分为2 个部分4 种情况方便之后的处理。Lin等［83］提出了FUP-HUI-MOD 算法在事务修改的数据集上挖掘高效用模式，提出了FUP 概念，通过TWU 将1 项集分为两个部分。

5 下一步的研究方向

通过对动态数据上的高效用模式挖掘算法的描述及总结可以看出现有的方法仍然存在许多不足，可以从以下几点进行下一步的研究。

1）动态利润数据集［24］上的紧凑高效用模式挖掘算法。

商品的效用会随着季节、政策等因素不断变化，促使同一商品产生不同的利润。目前大多数算法都以静态商品效用为前提来挖掘高效用模式，这种假设并不成立，导致许多算法并不能应用于实际生活中。此外，在高效用模式挖掘算法中挖掘出的模式往往很多，可对模式进一步精简，挖掘紧凑高效用模式如最大高效用模式、闭合高效用模式以及topk的高效用模式。为了发现更有趣的模式，在动态利润数据上挖掘紧凑高效用模式有很大的现实意义，我们下一步的研究方向是使用列表结构存储效用信息，在动态利润数据集中挖掘紧凑高效用模式，进一步提升算法的性能。

2）不确定数据流上的高效用模式挖掘算法。

在复杂的实际生活中，数据来源嘈杂、数据传输失败或数据丢失会引发数据的不确定性［84］。目前，大多数高效用模式挖掘算法均基于精确的数据集，很难用于处理不确定数据集。并且，现存的两阶段的、基于树结构、列表结构的不确定数据集上的高效用模式挖掘算法仅用于静态数据，现实场景的数据往往到达速度快，数量大。因此，在不确定数据流上挖掘高效用模式具有一定的研究意义。

3）数据流上的定量高效用模式挖掘算法。

目前存在的大多数高效用模式挖掘算法仅挖掘出了高效用的项集，并未给出所挖掘项集关于数量的信息，项的数量信息有利于做出更准确的营销策略。现阶段，定量高效用模式［85-86］挖掘的算法较少，且都应用于静态数据上，算法的运行时间、内存消耗等性能亦可进一步提升。在数据流上挖掘定量高效用模式对现实生活场景具有重要作用，使用滑动窗口并运用数据库投影技术的定量高效用模式挖掘、提高算法性能为一个可参考的方式。

4）分布式的高模糊效用模式挖掘算法［87］。

HUIM 通过涉及模式表示的数量来显示关键信息，不能提出诸如“大量购买尿布的人意味着少数人购买啤酒”之类的关系，此外，其基于预定义的最小效用阈值的二元模型来确定项集，不适用于当前的大数据环境的现实场景。为了解决以上限制，可以使用模糊集理论和Spark 及MapReduce，来挖掘更灵活、有效且数量庞大的知识；还可以考虑将分布式框架与深度学习架构结合处理更复杂的模式如模糊高效用模式挖掘。

6 结语

本文总结了动态数据上的高效用模式挖掘算法，包括在增量数据、数据流、动态删除和动态修改数据上挖掘高效用模式的算法。本文从数据结构、剪枝策略、优缺点等角度对增量数据上的算法进行了分析，并通过算法实验数据与复杂度对算法的性能进行了进一步的分析，还从算法使用的窗口模型介绍了数据流上的高效用模式挖掘算法，且对不同窗口的算法的性能进行了对比。此外，还介绍了动态删除和动态修改数据的高效用模式挖掘算法。除了介绍了高效用模式算法，还介绍了高平均效用模式、高效用序列模式，top-k高效用模式等挖掘算法。

动态数据上的高效用模式挖掘更适用于现实场景，但仍有不足，提出了动态利润数据集上的紧凑高效用模式挖掘算法、不确定数据流上的高效用模式挖掘算法、数据流上的定量高效用模式挖掘算法以及分布式的高模糊效用模式挖掘算法作为进一步的研究方向。