基于参数分析法的GNSS测波浮标波浪方向谱估计

谷汉斌，王成成，单 瑞

(1.宁波大学 土木工程与地理环境学院/海洋工程研究院，宁波 315211；2.同济大学 测绘与地理信息学院，上海 200092；3.中国地质调查局青岛海洋地质研究所，青岛 266237)

随着全球导航卫星系统(Global Navigation Satellite System, GNSS)技术的不断发展和进步，尤其是实时精密单点定位技术(Precise Point Positioning，PPP)的不断完善，给海洋波浪观测提供了便捷高效的手段[1-2]。GNSS浮标测波避免了原有的以惯性测波浮标为主的测波技术对浮标的高度的技术要求，如“波浪骑士”，如此小的浮标，直径0.4 m、0.7 m和0.9 m，内部设液体稳定平台，重力摆保持垂向加速度计始终处于垂立姿态；电子陀螺仪保持北向，其他两个水平加速度计、两个纵摇和横摇传感器、电池等密闭封存在这样的小空间内，给高精度浮标测波带来很高的技术要求。而高精度GNSS测波浮标可以通过PPP技术确定浮标的升沉和水平方向位移，动态测量精度达到厘米级，给海洋波浪测量提供了一种新的手段。其比GPS测波浮标采用的定位卫星多，抗干扰更强；当然，其算法和装置也有优化的空间。

海洋波浪分析包括统计学分析和谱分析方法[3]。最传统的波浪数据分析是统计分析法，针对水面升沉运动给出波浪统计参数，以便于工程应用。随着对海洋波浪观测和分析研究的深入以及数学上随机过程的理论发展，谱分析方法越来越受到重视[3-5]。波浪谱分析方法包括频谱分析和方向谱分析，频谱分析只在频域上进行，不考虑空间的分布特性，频谱分析包括相关函数法、傅立叶变换法(FFT)和最大熵法(MEP)等，其中前两种方法简单易行；波浪的方向谱分析法不仅包括了波浪在频域上的变化，还考虑方向上的分布，其中有直接傅立叶变换法(DFTM)、参数法、最大可能伸展法(EMLM)、最大熵法、贝叶斯法(BDM)、最大熵延申法(EMEP)等方法[5]，其中参数法是比较容易实现的方法，只需要升沉和水平方向三组位移过程就可以分析波浪的方向谱。当然，近些年波浪谱的研究也有很大发展，如采用小波变换分析海洋波浪方向谱[6]、采用声学多普勒流速剖面仪(ADCP)估计波向[7]和海浪方向谱的数据测量和估计[8]及波浪特征分析[9]等。近年来，波浪方向谱的估计和观测在国外也一直受到重视[10-11]。

波浪谱分析方法很多，它们各具优缺点。这里只讨论基于参数法的波浪方向谱生成，以及支持该方法的傅立叶变换在频域里的谱验证。该方法便于应用于高精度GNSS浮标测量波浪的数据分析。

1 GNSS测波浮标简介与处理程序包

GNSS浮标由1个主浮筒和3个辅浮筒组成，均为圆柱状，3个辅浮筒彼此等间隔120°，主浮筒直径约0.5 m，辅助浮筒直径约0.35 m，其顶部为GNSS接收天线，主浮筒内安装1台TRIMBLE NETR9接收机,见图1。GNSS浮标水上部分高约0.50 m，水下部分高约0.4 m，实验时采样频率为5 Hz。GNSS单元可测得该浮标高精度位置及速度变化。本文拟为该类浮标测波提供数据分析方法。

图1 GNSS测波浮标

基于Matlab程序设计了GNSS浮标的数据处理程序包，包括高频和低频数字滤波、波浪统计分析、波浪频谱分析和波浪方向谱分析，以及相关列表和图形显示功能。本文主要介绍波浪统计分析和波浪频谱与方向谱分析方法和结果。

2 波浪统计分析

波浪统计分析是最常用的波浪观测数据处理方法，通常按照工程应用需求，统计出平均波高、三分之一大波的平均波高即有效波高、十分之一大波的平均波高、最大波高等，以及对应的波浪周期。这里只讨论针对一个波浪系列的统计分析，波浪统计分析还包括如波浪重现期等相关的分析，不是这里讨论的重点。对于实测的波面位移时间变化 ，i=1,2……n，计算其平均值，该值为平均水平面，采用这个平均值对波面位移时间过程在位移时间坐标系内切割位移时间过程线，把位移零点平移到这个均值线，得到一系列跨零点，按上跨零点法分析波高和周期，以从大到小的顺序排列，找出前述各特征波高。

图2 波浪出现方向和频次

(1)

将波浪骑士浮标原始数据采用式(1)计算各特征值，与波浪骑士处理软件W@ves21的分析结果进行对比，只有标准差比较接近，其他数据存在一些偏差(表1)，可能波浪骑士处理时，采用了不同的滤波或分段方式。对波浪骑士测得的升沉和两个水平方向位移进行相关分析，相关系数计算值与其处理结果一致，升沉与南北向位移相关系数0.13，与东西向位移为0.004，南北向位移与东西向位移相关系数0.76。采用升沉数据进行波高统计分析的对比结果见表2，波高和周期的统计值相差基本接近。

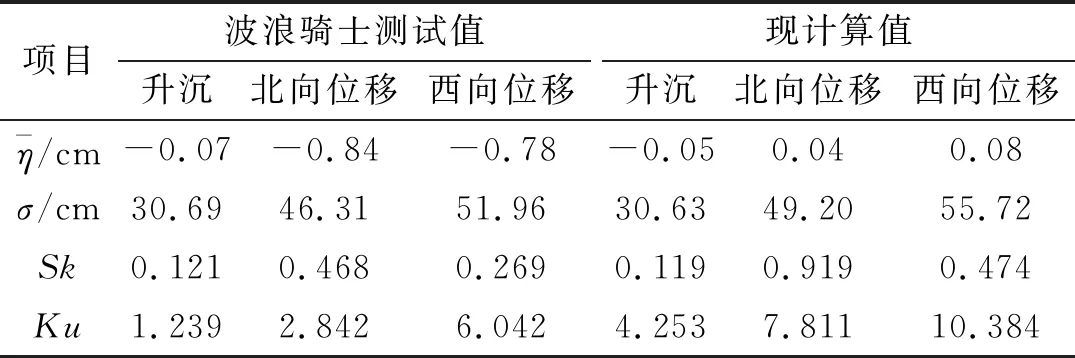
表1 数据前处理结果对比

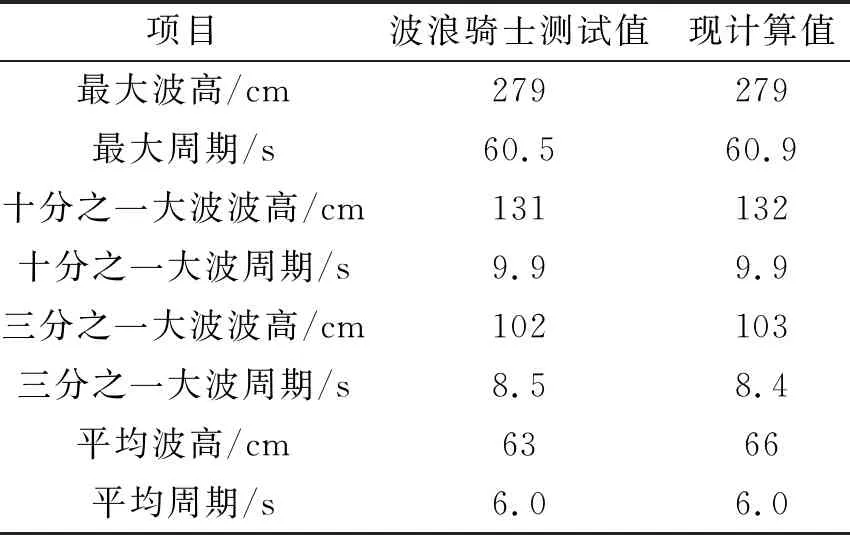
表2 统计波高和周期对比

3 频谱生成方法与验证

假定波面垂直向上位移时间过程η(t)是一个平稳随机过程，傅立叶变换将其变换到频域X(ω)，即

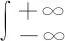
(2)

其逆变换为

(3)

这样频域和时域是一个相互变换的过程。因此，波浪频谱已知，可以通过谱分割的办法构造时间域的随机过程[3]。由于随机相位的引入，一个波谱可以生成无数个随机过程，但是这些随机过程对应一个频谱。目前常用的波谱有JONSWAP谱、我国港口工程规范谱、PM谱等。给出波谱参数，波谱就能够表达出来；例如给定有效波高1.0 m、有效波浪周期8.5 s、水深50 m，采用JONSWAP谱，谱型见图3星点所示。对该谱进行分割200份，最小截断频率fp/5，最大取5fp，采用Longuet-Higgins不规则波模型构建出一个随机波面过程见图4。对这个随机波面过程进行逆变换分析，即为谱估计，采用快速傅立叶变换进行谱估计[3]，得到估计谱如图3黑线所示。快速傅立叶变换过程中，要注意(1)变换前使用截尾窗将整个随机波面过程看作一个长周期进行周期化，变换后去掉截尾窗影响；(2)快速傅立叶变换后的粗谱需要进行平滑处理；(3)傅立叶变换时，针对时间步长△t=1的时间系列，变换后的频域幅值要换算成对应实际△t的值；(4)由于很多计算机语言提供了傅立叶变换函数库，针对一般性问题，频域函数为复数，做波浪频谱分析时常采用实部，输出频谱时对频率输出点数进行了截半处理。

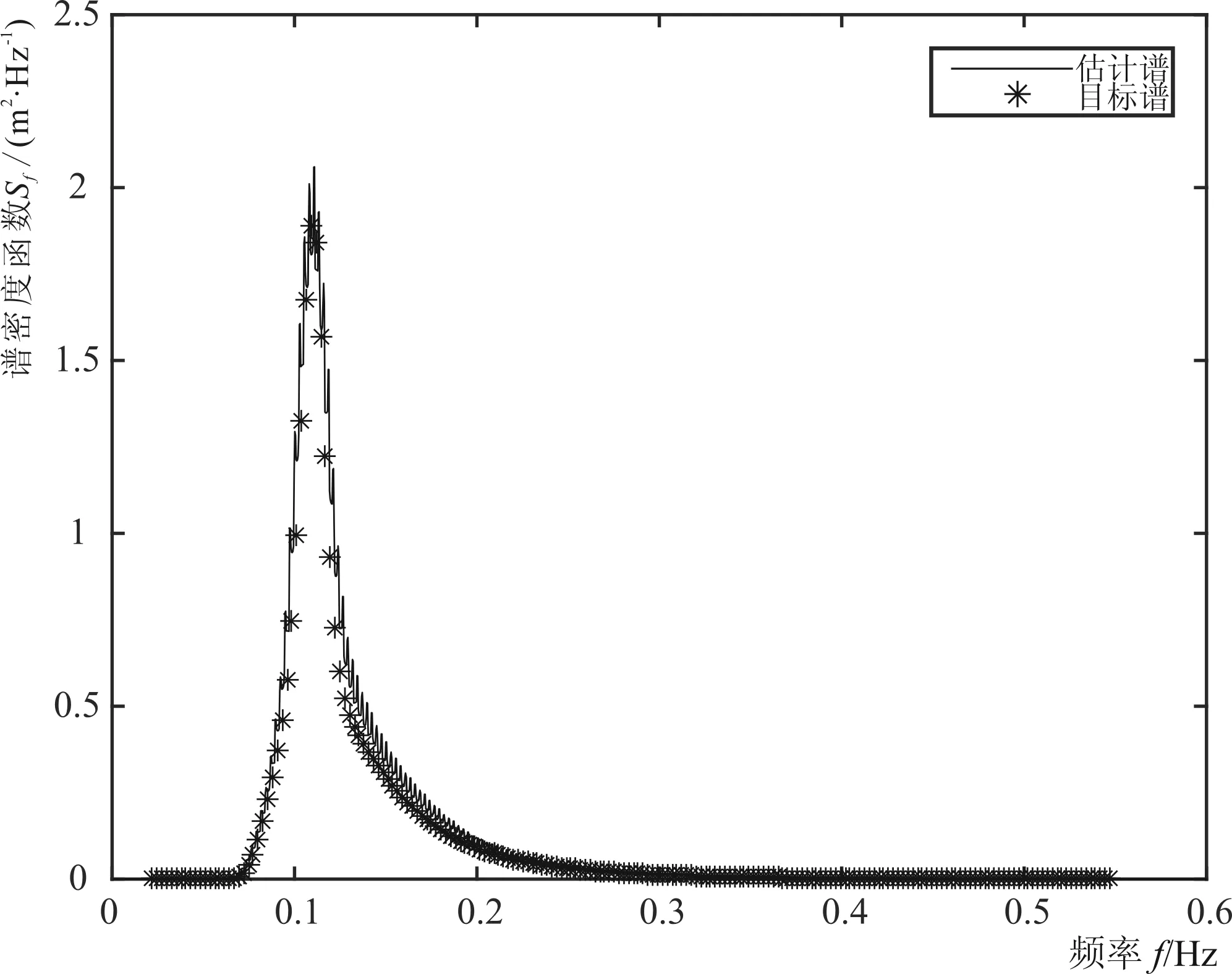
图3 JONSWAP计算谱与估计谱对比

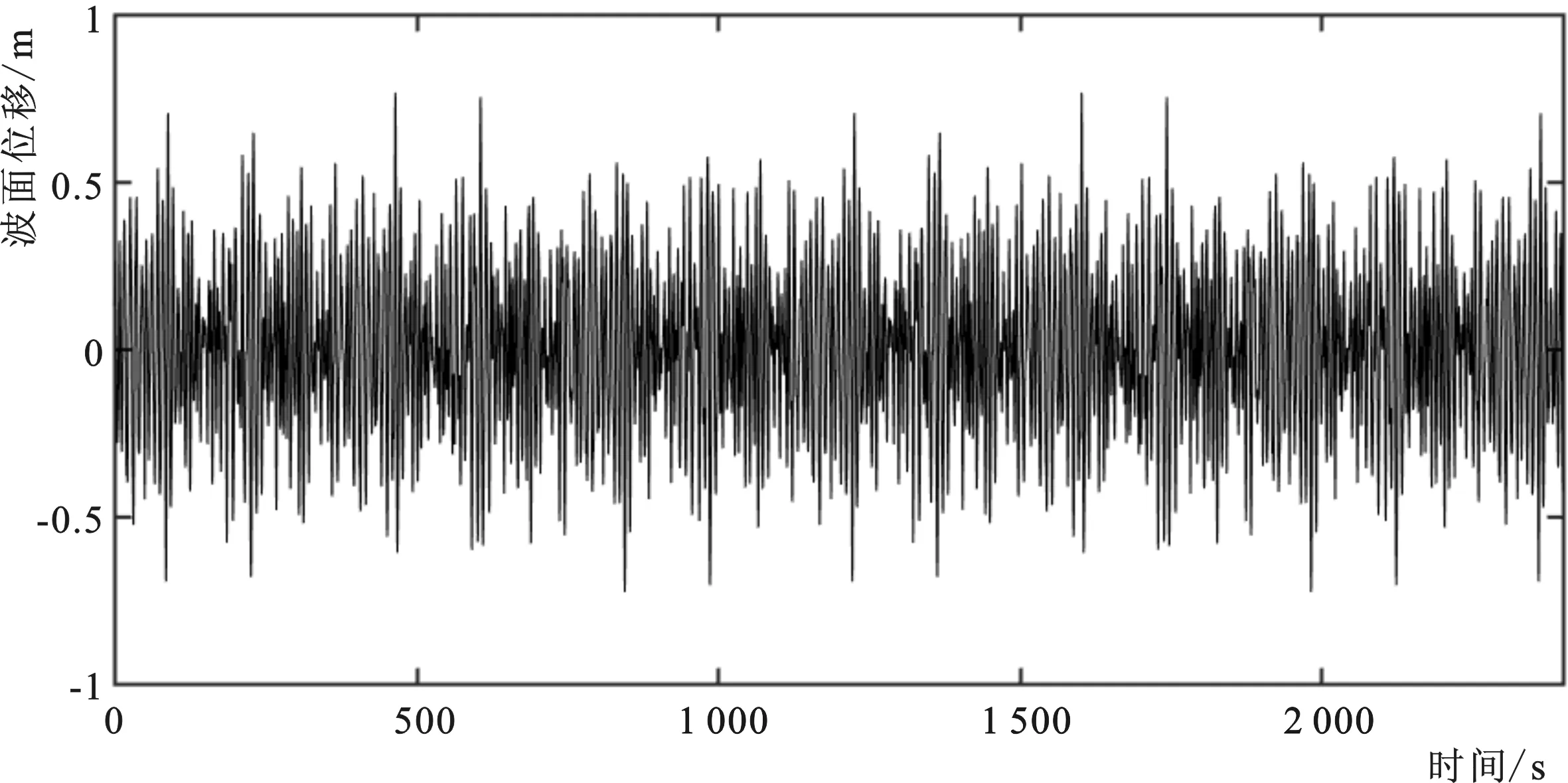
图4 波面垂向位移时间过程

4 方向谱估计方法

前文提到波浪方向谱有多种估计方法，其中参数估计法是一种简单易行的方法，该方法由LONGUET-HIGGINS等人提出[12]，BORGMAN[13]、PANICKER和BORGMAN[14]及HASSELMANN等人[15]对该方法进行了不断完善，分别提出截断的傅立叶系列、余弦函数幂次系列函数、圆形正态分布和正态分布等截断函数表示方向分布。其中截断的傅立叶系列形式最简单

S(f，θ)=S(f)[a0(f)+Σn{an(f)cos(nθ)+bn(f)sin(nθ)}]

(4)

式中：S(f，θ)和S(f)分别为波浪方向谱和频谱，后面方括号内的项为方向分布函数G(f，θ)，其中a0、an和bn为系数，f为频率。该式适用于浮标观测方向谱，并取得不少测波资料。理解其处理方法，更有助于理解观测数据。

在波浪骑士用户手册中，频谱采用升沉时间系列(图5)的傅立叶变换得到。采用本文验证的程序对该系列进行分析，结果见图6。与波浪骑士的处理结果基本一致，波浪骑士数据振荡更大一些，Smax=1.18，主频略小，本文计算Smax=1.2；低频部分也基本一致。这里有两点需要注意：(1)波浪骑士手册提到对原始数据采用两种滤波，周期分别为43 s和256 s；本文对数据系列采用滤波周期47 s。(2)频谱平滑处理时，平滑点数P[3]本文取N/160，N为傅立叶变换系列处理点数。

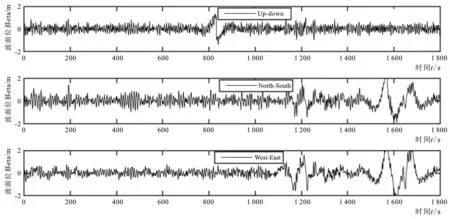
图5 某次浮标升沉和水平方向时间系列

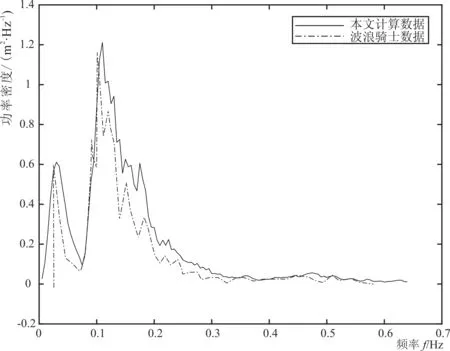
图6 波浪频谱

波浪骑士用户手册中方向分布函数表示为

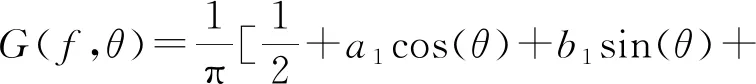
(5)

或表示为

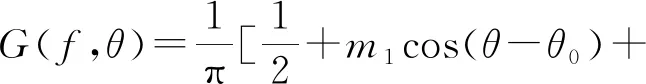
(6)

其中系数从浮标内部加速度传感器二重积分得到的升沉、水平方向位移时间过程序列(图5)的傅立叶变换的频域系数计算得到。对图5中3个位移时间系列进行傅立叶变换，从升沉、南北向和西东向位移时间系列分别得到频域傅立叶系数的实部与虚部αvf、αnf、αwf和βvf、βnf、βwf，傅立叶系数表示为

Avf=αvf+iβvf，Anf=αnf+iβnf，Awf=αwf+iβwf

(7)

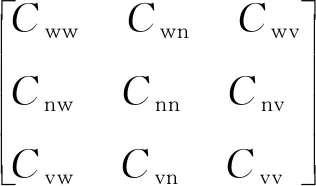
(8)

于是，可计算

(9)

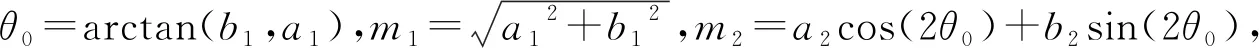
(10)

本文采用上述方法对图5的时间系列进行方向函数估计，结果见图7-a，采用式(5)或式(6)计算有一定差别，式(5)形成的方向函数在图中左侧，式(6)形成的在右侧。它们的共同点是方向函数的每个频率在各方向积分为1，但是都存在方向函数为负的方向，与物理意义不符。尽管伯格曼(Borgman)提出的平滑函数可以修正方向函数，使之非负，但降低了峰频，扩展了方向分布范围[3]。本文建议，对方向函数修正的具体做法可采用如下步骤：(1)求方向函数为负的积分面积，方向函数为负值时调整为零；(2)把负数的积分面积按面积权数分配到方向函数为正的部分，修正正的方向函数；(3)检验修正后的方向函数的各方向积分为1。按这一修正方法，修正后方向函数分布见图7-b。

7-a 由式(5)和式(6)分别估计的方向函数 7-b 式(5)和式(6)分别估计方向函数的修正结果

基于波浪的频谱和方向函数分布，给出方向谱S(f,θ)，如图8所示，其中图8-a方向函数分布按式(5)计算，图8-b按式(6)计算；基于两个公式的计算相差不多。需要注意，按式(6)计算前需要计算波浪方向角θ0，该角度为方位角，而在浮标上角度是按北向a1和西向b1为正计算的角度，该角度要换算为方位角，否则方向谱谱峰位置会出错。计算结果的主要参数与波浪骑士结果对比见表3，本文计算值都偏大，应该和滤波有关。

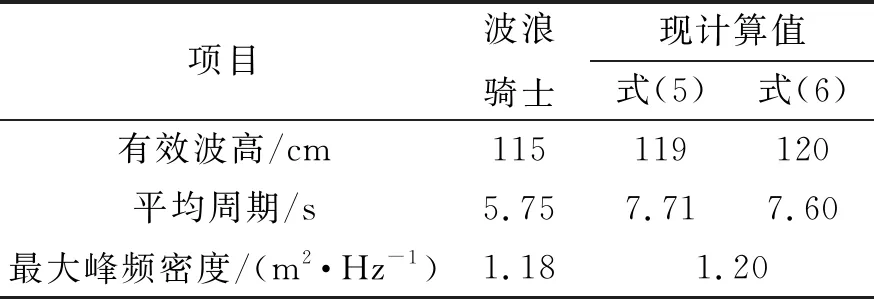
表3 统计波高和周期对比

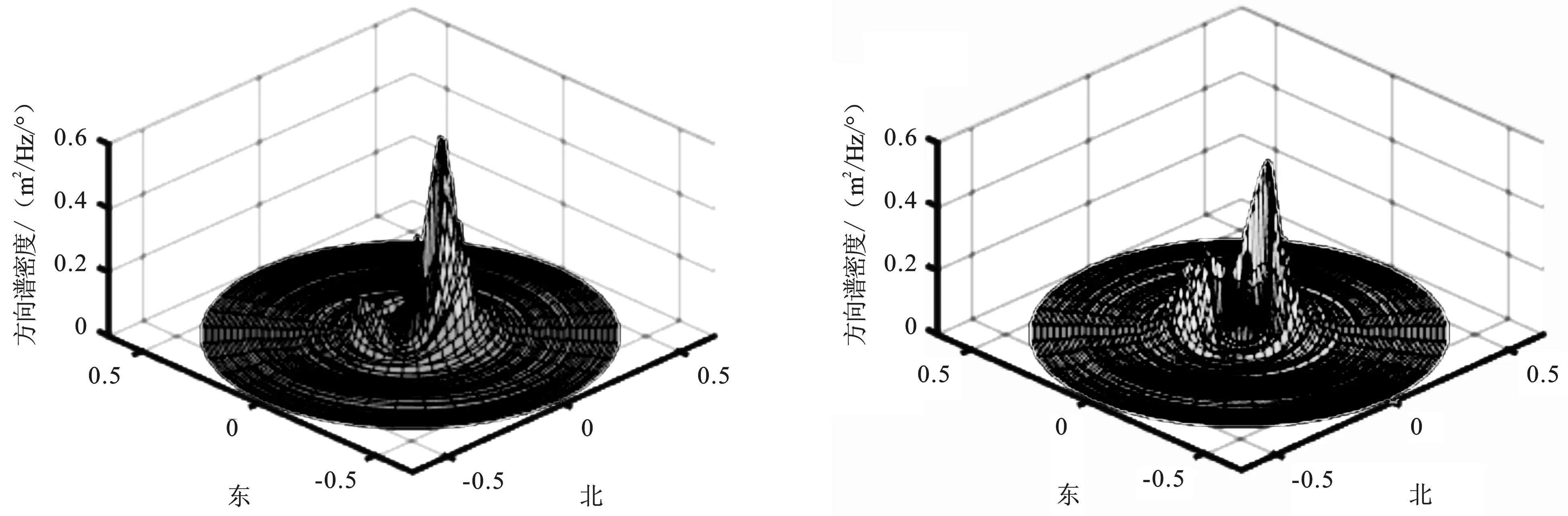
8-a 按式(5)计算的方向谱 8-b 按式(6)计算的方向谱

5 在GNSS测波浮标中的使用

将上述波浪方向谱估计方法应用于GNSS测波浮标，用于波浪观测，实测数据包括浮标升沉和两个水平方向N和E的水平位移，在浮标受海流和风的影响比较小的情况下，该浮标可用于波浪数据观测。图9给出浮标受波浪作用产生的升沉及两个水平位移时间过程。根据位移时间过程采用分析程序进行分析计算，结果见图10。从实测波浪方向频率图可以看出，波浪主要出现在东北和西南方向；峰频接近0.13 Hz，最大谱密度接近0.43；方向分布函数与实际波浪出现方向一致，同时给出了方向谱。统计H1/3=0.81 m，Hm0=0.98 m比统计值略大，统计平均波浪周期3.69 s，谱计算平均波浪周期4.00 s，也比统计值略大。总体看方向谱计算方法得到的结果基本可信。

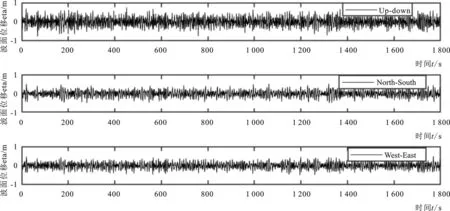
图9 高精度定位浮标位移时间过程

图10 数据分析结果

6 结论

本文针对GNSS浮标应用于测波的波浪数据处理方法，参考波浪骑士手册对实测结果进行了处理方法研究。给出了波浪统计处理方法、频谱处理方法和方向谱处理方法，对数据处理方法进行了编程，形成一套适用于高精度GNSS测波浮标的程序包。在波浪方向谱分析中，方向函数易出现负值，与物理定义不符，提出了修正方法。数据处理结果基本与波浪骑士处理结果一致，方向谱计算结果也与统计分析结果基本一致。说明该程序包可应用于高精度GNSS浮标对波浪进行海上观测。