一种检测用可变刚度连续型机器人设计

李强，王化明

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

连续型机器人是一种新型机器人，不同于传统机器人。连续型机器人采用形状灵活可变的柔性主干，具有优良的弯曲性能，可以柔顺而灵活地改变自身形状。由于结构的特殊性，其本体刚度低，承载能力差，外部负载对机器人的形状影响大，但可变刚度连续型机器人可实现机器人本体抵抗阻力和顺应外力之间的转换[1]，提高其使用的安全性，在提高承载能力的同时减小外部负载对机器人形状的影响，更加灵活地适应使用要求。

目前连续型机器人主要通过结构内部摩擦、材料特性、拮抗原理等实现变刚度。LOSCHAK P M等[2]采用塑料椎骨为主干，椎骨之间以球面相互接触，通过张紧拉线使椎骨之间相互挤压，增大界面处相对滑动的摩擦力，从而增加整体刚度。KIM Y J等[3]设计的用于微创手术的变中线刚度可调连续型机器人通过改变驱动线张力大小实现刚度的改变。耿仕能等[4]设计了锁紧机构，通过电流控制温控记忆合金(SMA)弹簧的收缩以增加连接盘与驱动丝之间的接触压力，从而提高接触点的摩擦力，提高连续型关节整体抵抗外力变形的能力。JIANG S R等[5]针对连续机械手模块提出了基于形状记忆合金(SMA)变刚度护套的概念，根据护套两端之间的电压以及奥氏体和马氏体之间的SMA相变来连续调整护套的刚度。HAO L N[6]和LIU Y G等[7]设计出基于气动人工肌肉(PAM)的连续型机器人，可控制不同气动肌肉内的压强，通过气动肌肉之间的拮抗作用实现机器人整体刚度的改变。除上述方法外，颗粒阻塞和层阻塞[8]也是常用的实现变刚度的方法。

目前连续型机器人变刚度方法主要存在以下局限性：1)机器人的工作环境受限，不适用于水下等特殊环境；2)只能实现柔性关节竖直状态下刚度的改变，当关节处于弯曲状态时未知；3)机器人整体结构复杂，变刚度附属机构冗余。本文介绍了一种可变刚度连续型机器人，其结构紧凑，在柔性关节处于不同弯曲角度状态下均可通过改变驱动线张力实现变刚度。

1 结构设计及运动学分析

1.1 柔性关节设计

柔性关节采用以螺旋弹簧为弹性主干的中空薄壁铰接式结构，其中铰接单元的结构如图1所示。

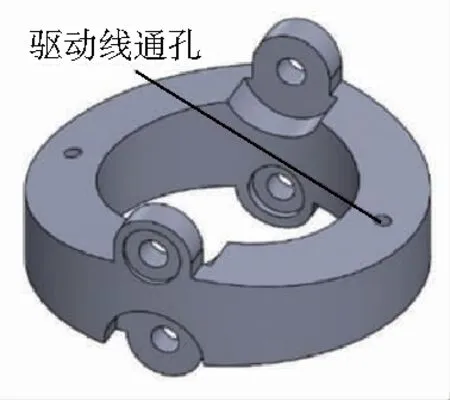
图1 柔性关节的铰接单元

图2所示柔性关节的整体结构由12个铰接单元和支撑架组成的铰接结构以及螺旋弹簧组成，弹簧的自由长度比铰接结构内孔稍长，装配时处于压缩状态。

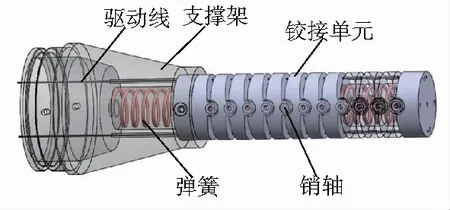
图2 柔性关节整体结构图

1.2 驱动结构设计

驱动部分由电机和蜗轮蜗杆组成，与气压驱动相比，电机驱动装置简单，工作稳定，控制精确。为保证驱动部分结构的紧凑，电机选用直流无刷减速伺服电机，其外径为22mm，工作电压为12V，输出轴转速为154 r/min，最大可提供64mN·m的转矩。蜗轮蜗杆的中心距为9.5mm，减速比为1∶20，可实现自锁以保证柔性关节的弯曲姿态不变。驱动部分的结构如图3所示，电机轴的旋转通过蜗轮蜗杆机构转化为绕线轮的旋转，进而实现驱动线的伸缩。

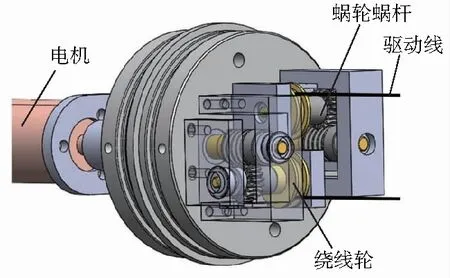
图3 驱动部分结构图

1.3 运动学分析

在建立柔性关节的运动学模型前，首先做如下假设：1)驱动线自身的长度变化可以忽略不计；2)驱动线的缩短会引起铰接单元之间的均匀旋转。考虑到柔性关节的结构，如图4所示，在每个铰接单元上建立坐标系{Oi}，其中i=1,2,…,13。由于底部单元固定在支撑架上，因此坐标系{O1}即为世界坐标系，顶端坐标系{O13}是坐标系{O12}沿z轴平移ltip得到的，对于其他的坐标系都是通过旋转和沿z轴平移l(单元高度)得到的。

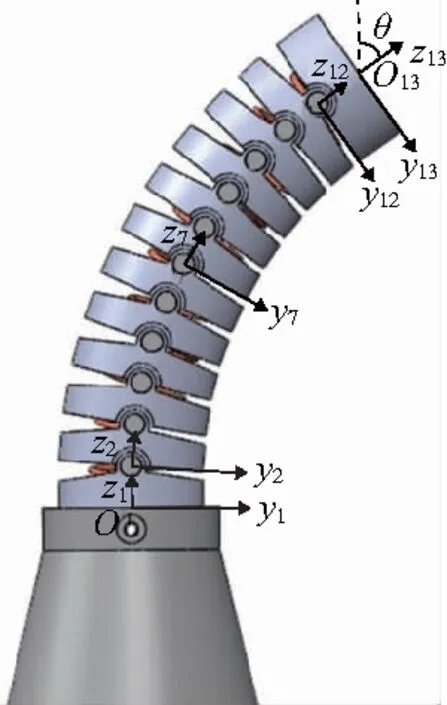
图4 柔性关节坐标系图

当一根驱动线LC缩短s时，另一根驱动线FC伸长，柔性关节弯曲角度为θ，每个单元相对旋转角度为θ/N(N=11)。如图5所示，根据几何关系，可以得到驱动线LC的缩短量s与弯曲角度θ之间的关系如下：

(1)

其中r为驱动线通孔的分布半径。

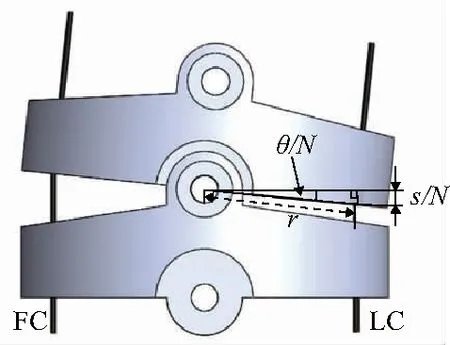
图5 柔性关节单元几何模型

以坐标系{O1}原点O1点为参考点，柔性关节顶端中心位置可以通过坐标系之间的转换得到：

(2)

其中：

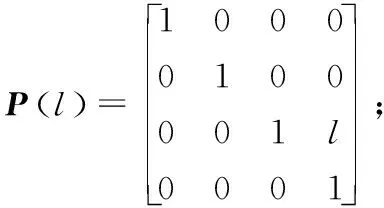
计算后得到的转换矩阵可表示为：

(3)

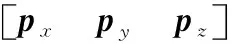
2 变刚度原理分析及仿真验证

2.1 变刚度原理分析

以下分析通过改变驱动线张力实现柔性关节刚度改变的原理。首先对连续型机器人的刚度进行定义，如图6所示，在驱动线FC和LC的作用下柔性关节弯曲角度为θ。此时在柔性关节顶端施加y轴(z轴)方向上的外力Fe，沿y轴(z轴)产生相应的位移△y(△z)，定义Fe/△y(Fe/△z)为y轴(z轴)方向上的刚度。

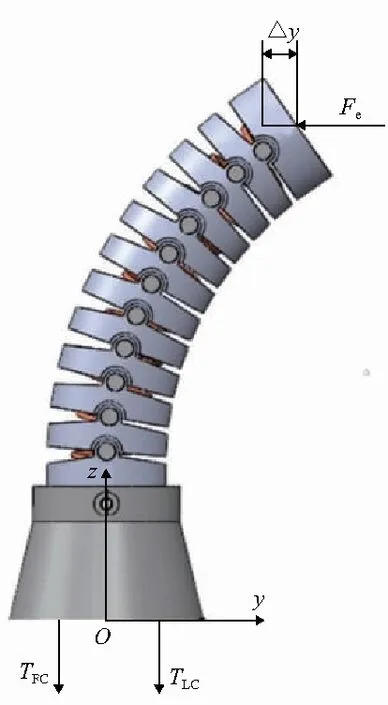
图6 柔性关节刚度定义图

对柔性关节中的每个铰接单元(除顶端单元)建立力学模型，如图7(a)所示。忽略单元通孔内壁与驱动线之间的摩擦，设驱动线上张力处处相等。以驱动线LC与铰接单元A接触点P1为例，分析P1点的受力情况。如图7(b)，P1点是驱动线上的点，TL是驱动线的张力，FN1是点P1所受到的支持力，f1为驱动线与铰接单元间的摩擦力。其中β=θ/N，γ=β为驱动线张力与单元A底面法向夹角，由于β较小，α≈β/2。所以摩擦力f1为

(4)

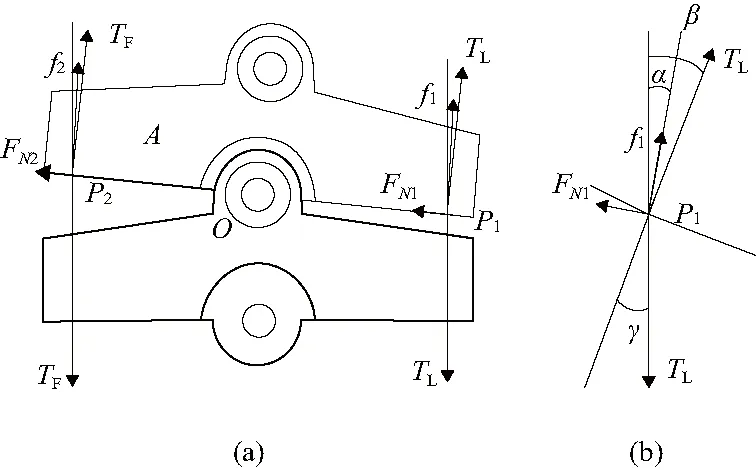
图7 铰接单元力学模型图

式中μ为摩擦系数。考虑到当铰接单元A绕轴O发生相对旋转时，需克服旋转副处的滑动摩擦力矩Mf，由于单元的相对旋转角度θ/N较小，因此只需要考虑驱动线张力法向分量对旋转副支持力NO的影响，即

(5)

摩擦力矩为

Mf=NOρ

(6)

式中ρ为旋转副摩擦圆半径。

当在柔性关节顶端单元施加外力时，内部铰接单元发生相对转动，关节整体表现出姿态的变化。在不考虑驱动线自身长度变化的前提下，施加的外力主要克服关节结构内部的摩擦以实现姿态的变化。已知这些摩擦力和摩擦力矩的大小与驱动线张力相关，因此可通过增大驱动线张力以增加柔性关节结构内部的摩擦力，进而增强关节抵抗外力变形的能力，实现刚度的增强。

2.2 柔性关节的Adams仿真分析

为验证变刚度方案的可行性，在Adams中建立建立柔性关节的力学模型(图8)，用以分析整体刚度与驱动线张力之间的关系。

首先将SolidWorks中的柔性关节三维模型导入到Adams中，其次添加相应的连接运动副，用作用力代替驱动线，用铰接单元间的扭转弹簧阻尼器代替螺旋弹簧，添加转动副的摩擦力以及驱动线与通孔间的摩擦力。

图8 柔性关节的Adams力学模型

通过改变驱动力TF和TL的大小，保证柔性关节弯曲角度不变，在顶端单元中心处分别施加水平方向上大小不同的外力Fe，测量力作用点的位移△y，得到的外力-位移关系斜率即为柔性关节的刚度。通过对不同弯曲角度的柔性关节施加外力，得到数据如表1-表3所示。

表1 柔性关节刚度测量表(弯曲角度34.8°)

表2 柔性关节刚度测量表(弯曲角度52.9°)

表3 柔性关节刚度测量表(弯曲角度79.5°)

对于不同弯曲角度下的柔性关节，根据表1-表3的数据分别绘制柔性关节刚度-驱动线张力的散点图，并进行直线拟合，得到图9的结果。从图9中可以得到以下结论：1)当柔性关节弯曲角度不变时，随着驱动线张力的增加，刚度也随之增大，且刚度与张力之间存在线性关系；2)驱动线张力相同时，不同弯曲角度的柔性关节对应的刚度也不同，弯曲角度越大，关节y轴方向的刚度越大；3)柔性关节的弯曲角度不同，驱动线张力对刚度的影响因数(拟合直线的斜率)也不同，弯曲角度越大，影响因数越大。仿真结果验证了通过驱动线张力实现柔性关节变刚度方案的可行性。

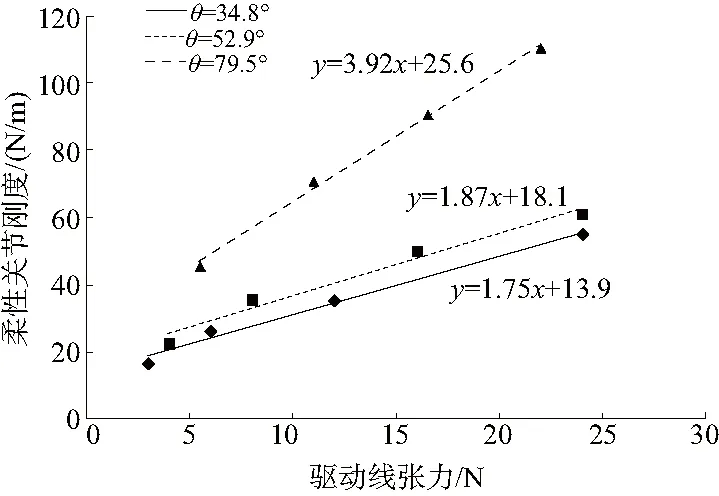
图9 柔性关节刚度与驱动线张力关系图

3 连续型机器人的实验验证

3.1 连续型机器人系统

实验所采用的连续型机器人系统主要由PC、直流无刷伺服电机、拉力传感器、柔性关节以及刚度测量平台组成，如图10所示，PC用于伺服电机的控制以及拉力信号的读取，伺服电机作为驱动部分，通过蜗轮蜗杆机构传递运动实现柔性关节的弯曲，拉力传感器用于驱动线张力的采集，刚度测量平台用于柔性关节尖端刚度的测量。

图10 连续型机器人系统

3.2 运动学模型的验证

为验证1.3节所提出的运动学模型的正确性，需要测试的柔性关节弯曲角度分别为：15°、30°、45°、60°、75°和90°。实验时把通过运动学模型计算得到的驱动线长度变化量转化为伺服电机的位置信号，通过控制电机实现柔性关节的弯曲，如图11所示。将柔性关节末端的实际位置与理论位置进行比较，可以看出两者相差不大，而且基本一致，这说明了所提出的运动学模型具有一定的准确性。

图11 运动学验证图

3.3 变刚度方案的验证

为验证连续型机器人刚度与驱动线张力之间的关系，在柔性关节末端安装了刚度测量平台。该测量平台由微型滑台和压力传感器组成，通过转动手柄使关节末端在y轴方向上分别产生1mm、2mm和3mm的位移，所得到的压力值与对应位移量拟合直线的斜率即为柔性关节末端在y轴方向的刚度。

图12 刚度测量平台

在实验中，分别选取了30°、60°和90° 3个柔性关节弯曲角度，在保证弯曲角度不变的前提下，增加驱动线的张力，分别测量关节末端刚度得到的结果如图13所示。

图13 刚度-张力关系图

从图13中可以看出：1)柔性关节末端刚度与驱动线张力之间存在线性关系(90°时不明显)，随着驱动线张力的增加，关节末端刚度增大，但并不会无限制地增长，在张力达到一定值时刚度会发生突变；2)柔性关节弯曲角度不同时，驱动线张力的变化对刚度的影响程度不同，且关节弯曲角度越大张力变化对刚度的影响程度越大；3)驱动线张力相同时，关节弯曲角度越大，刚度越大。可以看出这些结论与2.2节中推测的相同，证明了所提出的变刚度方案的可行性。

4 结语

本文设计了一种用于检测的可变刚度连续型机器人，提出了机器人的运动学模型并通过实验加以验证；提出了通过改变驱动线张力实现连续型机器人变刚度的方案，建立Adams模型并进行了仿真验证；最后通过实验验证了所提变刚度方案的可行性。本文从驱动线张力入手，为可变刚度连续型机器人的研究提供一个新的思路。