基于840Dsl CNC的机器人精确控制技术

蒲玉潇，田威，李鹏程，李宇飞

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

机器人进行高精度作业任务时主要依靠其绝对定位精度与轨迹精度，而通常情况下机器人本体重复定位精度较高，在±0.08mm以内，而绝对定位精度与轨迹精度较低，绝对定位精度达(±1～2)mm[1]，轨迹精度可达(±2～4)mm[2]。因此研究提高机器人定位精度与轨迹精度是推动智能制造技术发展的关键技术。

根据补偿作用位置不同，可将机器人精度补偿方式分为离线补偿与在线补偿。离线补偿通常是由事先建立好的误差模型计算出目标位置的修正值，将修正过后的控制量发送给机器人控制器，使机器人达到期望位姿的精度补偿方式，通常采用前馈控制的方式。周炜[3]等提出一种基于空间插值的精度补偿方法，通过在机器人工作空间中划分网格并根据反距离加权的方法来估计机器人目标点位处的位置误差来进行补偿，但此方法补偿效果受采样步长大小影响显著。XU W L等[4]利用前馈神经网络对机器人关节转角误差进行预测，并通过控制系统对关节转角误差进行补偿来提高机器人末端定位精度。ZENG Y F等[5]证明了末端位姿误差具有相似性，并据此建立末端位姿误差预测模型，对机器人进行精度补偿。以上精度补偿方法适用性较为广泛，高度依赖机器人的重复定位精度，但只能在采样空间内才可有效提高精度，若转换工作空间后补偿会失效。

在线补偿通常是在机器人关节轴上或者末端执行器上附加外部检测设备，通过实时获取关节角或末端位姿并输入至控制器中对其进行反馈修正控制，从而保证机器人的定位精度。如美国某公司对KUKA机器人进行改造，在各关节处安装光栅尺，采用840Dsl数控系统直接控制机器人，采用关节反馈的控制方式对机器人进行高精度控制，其绝对定位精度达到±0.25mm[6-10]。该方法可有效减小关节转角误差，提高机器人的重复定位精度，但却忽略了除关节转角误差之外的误差源所带来的误差。德国的弗劳恩霍夫协会利用T-Mac在线实时测量机器人位姿，通过激光跟踪仪在线测量反馈控制机器人，其轨迹精度可达±0.35 mm[11]。浙江大学采用激光跟踪仪全闭环控制方法，对机器人末端作业位姿在线测量与修正，使机器人绝对定位精度提高到±0.2mm[12]。该控制方法精度较高，但是高度依赖外部视觉以及激光设备，对加工现场环境要求较高，且成本较高。

本文将离线补偿与在线补偿相结合，提出基于西门子840Dsl CNC的前馈补偿与关节反馈控制相结合的方式，对机器人末端位姿与轨迹进行修正。最终通过实验表明该方法可有效提高机器人的定位精度与轨迹精度。

1 基于840Dsl CNC的精度补偿

1.1 西门子840Dsl数控系统直驱方案

数控系统与机器人原本控制系统相比，具有较高的开放性以及优秀的动态性能。通过采用数控系统来直接控制机器人不仅可以提高机器人的运动精度和动态响应能力，还可将数控系统中各功能模块集成应用到机器人的相关控制中。因此，本文将KUKA原有的KRC4控制器移除，采用西门子840Dsl CNC直接驱动机器人电机，以完成各项作业任务，其原理如图1所示。

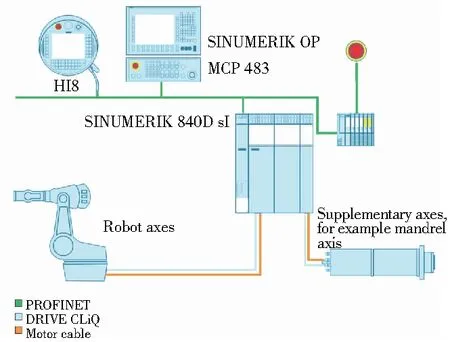
图1 西门子直驱控制方案

1.2 前馈补偿算法的系统集成

由于D-H模型中机器人运动学参数连杆杆长ai、连杆偏置di、关节扭角αi以及MD-H模型中的附加参数βi均为常量，只有关节转角θi为变量，在关节约束量一定时，末端位姿对应着唯一一组机器人关节逆解，即关节转角与末端位姿存在映射关系。因此末端位姿误差与关节转角误差也存在映射关系，即

ΔP=f(Δθ)

(1)

由机器人末端误差在笛卡儿空间具有相似性[6]可知，机器人末端误差在关节空间也具有相似性。

机器人末端定位误差可分为系统误差和随机误差，用线性回归方程可描述为

el(θ)=ρ(βl,θ)+gl(θ)，l=x,y,z

(2)

式中：θ=[θ1,θ2,…,θn]T为n自由度机器人上一点的关节输入；l为笛卡儿空间方向，在各方向上的计算方式相同；ρ(β,θ)为回归方程的线性部分即系统误差，其形式如下：

ρ(β,θ)=β1+β2θ1+…+βn+1θn=[1θ1…θn]β=

f(θ)Tβ

(3)

g(θ)为回归方程的随机部分即随机误差，满足期望为0，即E(g(θ))=0，且任意两组关节输入g(θ)(i)和g(θ)(j)对应的协方差为

Cov(g(θ)(i),g(θ)(j))=E(g(θ)(i),g(θ)(j))=σ2S(ξ,θ(i),θ(j))

(4)

式中：σ2为采样点在l方向的方差；S(ξ,θ(i),θ(j))表示以ξ为参数的相关性模型。本文采用高斯模型作为相关性模型。

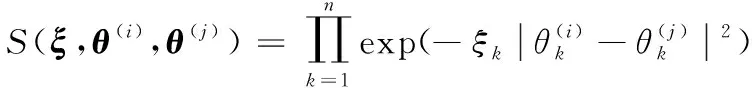
(5)

式中：m为采样点的个数；ξk∈ξ，为第k个关节输入角度的模型参数，可通过极大使然估计求得：

(6)

式中：R∈Rm×m为相关性矩阵，该矩阵中的元素表示两采样点之间的相关性。

Ri,j=S(ξ,θ(i),θ(j))

(7)

由Kriging差值可知，在机器人工作空间中任意一点在l方向的估计误差可以表示为

(8)

式中：w∈Rm为目标点与采样点之间的权值矢量；e∈Rm为采样点在l方向上的误差矢量。

构建矩阵F∈Rm×n+1表示采样点关节输入：

F=[f(θ(1)) …f(θ(m))]T

(9)

构建相关性矢量r∈Rm表示目标点与采样点的相关性：

r(θ)=[S(ξ,θ(1),θ) …S(ξ,θ(m),θ)]T

(10)

利用线性无偏最优估计的方法求出权值w，应该保证目标点的估计值与实际值的差值是无偏的，即

wTG-g(θ)+(FTw-f(θ))Tβ

(11)

式中：G=[g(θ(1))…g(θ(m))]T。

要保证式(11)是无偏的，则需使：

FTw=f(θ)

(12)

为获得最优权值w，需使式(11)的方差最小，则：

δ2(1+wTRw-2wTr)

(13)

对上述问题的求解可转化为条件极值的求解，可通过拉格朗日乘数法解决，即

L(w,λ)=δ2(1+wTRw-2wTr)-λT(FTw-f(θ))

(14)

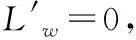
(15)

通过上述公式可求得w的最优值，将该值带入式(8)即可求解出目标点的估计误差。

本文利用SINUMERIK Integrate Create MyHMI/3GL编程包，使用Qt/C++编程语言来建立集成控制软件与数控系统的通信，将算法集成至数控系统中，实现关节输入的前馈控制，提高末端位姿精度。

1.3 半闭环反馈控制模型

本文采用图2所示的机器人关节电机三环反馈控制模型，即电流环、速度环和位置环，其中电流环主要调节电机的转矩。电机自带的相对式编码器作为第一编码器提供电流及速度信息反馈给电流控制器以及速度控制器，安装在机器人各关节处的绝对式光栅尺作为第二编码器将机器人关节转角信息反馈到位置控制器中。采用840Dsl CNC直驱机器人方案，其三环控制均在数控系统中进行，由数控系统中的NCU控制单元直接进行反馈处理。与在上位机处理位置反馈的方式相比，关节转角反馈更加迅速及时，可在每个12ms的插补周期内进行反馈控制，有效提高机器人的定位精度与轨迹精度。图2中的位置控制器、速度控制器和电流控制器均采用PID控制器，连续的PID控制模型如下：

(16)

式中：e(t)为误差信号；KP、KI、KD分别为比例参数、积分参数和微分参数。

将式(16)离散化，令：

(17)

则离散化后的PID模型为

(18)

图2 半闭环控制模型

第二测量系统即绝对式光栅尺的检测精度直接影响着半闭环反馈的控制精度，因此对光栅尺的标定是极为重要的一个环节。本文采用绝对式直线光栅尺作为第二测量系统，安装在机器人六关节外表面，如图3所示。由于所选第二测量系统为直线光栅尺，因此需采取以直代曲的方式，对其进行标定后，将光栅尺位置值转化为关节转角值后才可正确地反馈关节转角误差值。本文采用激光干涉仪、角度干涉镜和回转轴校准装置对直线光栅尺进行测量标定。

图3 机器人各轴光栅尺安装图

2 实验验证与结果分析

2.1 实验平台的搭建

搭建如图4所示的实验平台对半闭环反馈控制进行实验验证。采用改造后的KUKA KR500R2830MT型工业机器人作为精度验证对象。该机器人移除原有KRC4控制柜，采用840Dsl数控系统直接驱动机器人各关节电机，在机器人法兰盘上安装钻铣一体式末端执行器，使用激光跟踪仪作为测量设备，将靶标球固定在末端执行器上。

图4 实验平台

2.2 机器人重复精度测试实验

选取机器人运动范围内600mm×1 200mm×800mm的工作空间，根据《GB_T12642—2013工业机器人性能规范机器实验方法》，选取工作空间内5个点P1-P5,从P1-P5开始，按照P5—P4—P3—P2—P1的顺序循环30次，并用激光跟踪仪测量末端位姿。误差采用欧式距离进行计算，即

(19)

测量结果如表1所示。

表1 机器人重复性测量结果

对表1的实验结果分析可知，增加半闭环反馈控制后，使得机器人的重复定位精度得到提升，而机器人的重复定位精度是影响前馈补偿算法补偿精度的重要因素，因此机器人的精度将会得到进一步提升。

2.3 机器人绝对定位精度测试实验

选取与2.2小节中相同的工作空间，采用拉丁超立方法在该空间内随机生成500个采样点与300个验证点。采样点用于对前馈补偿算法的误差建模并测量机器人原本定位精度，验证点用于验证前馈补偿与半闭环反馈补偿共同控制作用下的机器人绝对定位精度。实验结果如图5所示。(本刊为黑白印刷，如有疑问请与作者联系)

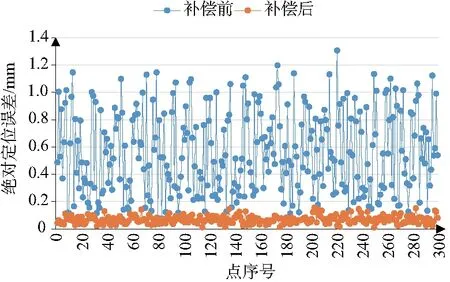
图5 补偿前后绝对定位误差对比图

对图5的实验结果分析可知，机器人的绝对定位误差最大值由原本的1.31mm提高到0.15mm，机器人的绝对定位精度提高了88%。实验证明通过关节半闭环反馈补偿后，机器人的精度得到大幅度改善。

2.4 机器人轨迹精度测试实验

选取与2.2小节中相同的工作空间，在该工作空间内规划一条直线和一条圆弧轨迹，使用激光跟踪仪跟踪测量末端位置，得到机器人运动轨迹离散图。

由图6、图7的实验结果分析可知，通过前馈控制与关节半闭环反馈控制的补偿方式，使机器人的直线轨迹精度由原先的1.89mm提高到0.28mm，圆弧轨迹精度由原先的1.34mm提高至0.28mm，轨迹精度提升了85%，实现了机器人轨迹的精确控制。

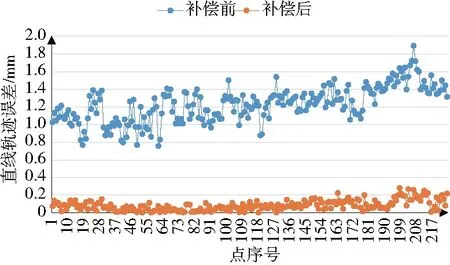
图6 直线轨迹误差

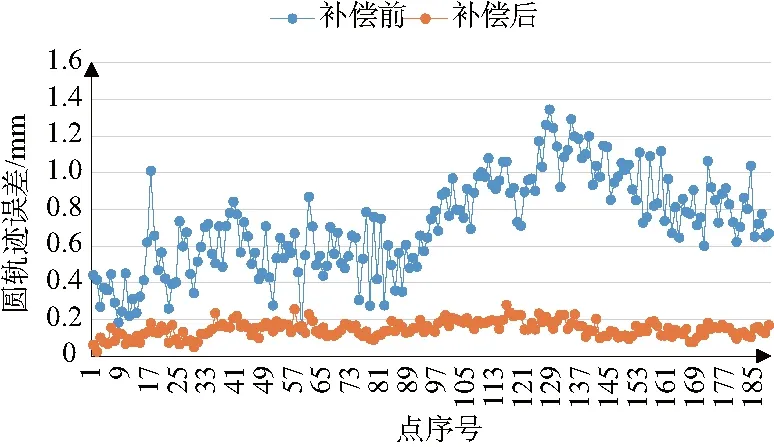
图7 圆弧轨迹误差

3 结语

采用西门子840Dsl数控系统直接控制KR500R2830MT型工业机器人，采用前馈补偿与关节半闭环控制相结合的精度补偿方式，将机器人的重复定位精度提高至0.04mm，绝对定位精度提高至0.15mm，轨迹精度提高至0.28mm以内，实现了工业机器人的精确控制，可应用于高精度智能加工领域。