核心素养下小学生数学思维品质的培养路径

☉刘树刚

数学学科核心素养体现在数学抽象、逻辑推理、数学建模、数学运算、直观想象等部分。“思维品质”由苏联心理学家斯米尔诺夫在其著作《心理学》中最早提出，体现个体在思维活动中呈现出的不同智力特征与表现差异。具体到学科，数学思维品质则体现为学生在数学活动中的个性思维特征。数学思维品质由敏锐性、灵活性、深刻性、批判性、创造性等五个维度构成［1］。笔者从教学实践入手，探寻核心素养下小学数学思维品质的培养路径。

一、从数学运算着手，培养学生数学思维敏锐性

数学运算是指运用数学相关公式法则，正确进行运算的综合能力。运算能力是一种数学思维能力，它是学生数学素养的核心。能否恰当掌握数学算理，能否通过合理简洁的运算途径来解决数学问题，是衡量学生数学思维品质优劣的重要指标，也是培养数学思维品质敏锐性的重要通路。我们要重视学生运算能力的培养，重视数学运算与思维敏锐性之间的关联，增强学生数学学习的敏感性。

加减法是数学运算的开始，也是低年级学生面对数学课程时最先学习的内容。看似简单、机械的加减运算学习中，实际蕴藏着对数学思维敏锐度的考察。在教学苏教版小学数学一年级上册《10 以内的加法和减法》时，有这样的一道练习题：8-3+2=？课堂练习中，有的学生这样计算：8-3=5，然后用5 和2 相加，得数是7，从而求得正确答案。但一些学生则敏锐地观察到8 和2 之间的“整十”关系，将运算过程简化为：8 和2 的和，然后再减去3，即8+2-3=10-3，从而求得题目答案7。我们知道，“运算律”是小学四年级才接触的学习内容，但在低年级数学运算课堂上，这样的思维敏锐度会经常发生，需要我们在教学中百般呵护。

二、从逻辑推理着手，培养学生数学思维灵活性

逻辑推理能力贯穿于整个数学学习过程，是数学学科的基本思维。逻辑推理需要学生借助已有数学经验和数学知识，按照既定规则，通过归纳、类比、证明、计算过程，寻求问题解决的过程。逻辑推理没有固定模式可以借鉴，凭借的是解题者的数学经验和数学直觉，体现了数学思维品质中的灵活性特点。要重视从逻辑推理着手，着眼于学生思维灵活性培养，以全面提升学生数学核心素养［2］。

在三年级《两、三位数乘一位数的估算》一课中提供了这样的问题情境：西瓜每箱48 元，哈密瓜每箱62 元，张大叔带了200元，买4 箱西瓜够吗？300 元够买5 箱哈密瓜吗？本题看似一个简单的应用题，实则反映出对学生基本逻辑推理能力的考察。常规解题思路是：（1）48×4=192（元），192 ＜200，所以，够；（2）同理：62×5=310（元），310 ＞300，所以，不够。一些思维灵活学生在严密逻辑推理基础上想到估算的方法解题，取得异曲同工之妙：（1）48 看成50，50×4=200（元），48×4 ＜200，所以，够；（2）同理：62 看做60，60×5=300（元），62×5 ＞300，所以，不够。由此可见数学思维的灵活，建立在严谨的逻辑推理基础之上，值得我们在小学数学课堂教学中认真总结应用。

三、从数学抽象着手，培养学生数学思维深刻性

数学抽象是利用数学概念、原理或方法等解释现实生活中数学问题的过程。数学抽象能力体现了学生由生活经验向数学问题迁移的思维过程，是学以致用和数学思维深刻性的体现。数学教材中的各种应用题型、图形与数量转换题型，均包含着大量对数学抽象思维的考量。实际教学中，我们要重视类似题型在日常课堂中的应用，以凸显它们对学生数学思维深刻性的影响和培养。

以四年级下册《解决问题的策略》例2 的教学为例：有一块长方形的草地，长8 米，在后期改建中，草地的长度增加了3米，面积相应增加了18 平方米。请问，原来的草地面积是多少？本题是将学生们常见的生活场景进行数学抽象处理的代表，考查学生对具体问题的数学抽象处理能力。按照题目意思分析，学生们通过作图很快找到解题思路：18÷3=6（m），8×6=48（m2）。但也有同学发现：在同样的宽度情况下，大的未知长方形面积与小的已知长方形面积（18m2）间的关系，应该是8 和3 大小关系的反应，即8÷3×18=48（m2），既是对小学六年级数学“等比例”思维的提前应用，也体现了在数学抽象能力应用过程中的思维深刻性。

四、从数学建模着手，培养学生数学思维批判性

建模能力是从不同数学情境中抽离出具体数学问题，通过数学符号、数学公式以及数学理论，进行模型构建的过程。数学建模体现了数学学习中的应用能力，在探寻数学模型间的数量关系和变化规律过程中，学生会自发反思对数学知识的掌控能力，提升数学思维中的批判能力，增强数学学习兴趣，进而提升数学思维品质和核心素养能力。

以四年级下册《三角形、平行四边形和梯形》这一单元中的一道题为例：把一根长为14cm 的吸管，剪成3 段，要求每段都是整厘米数，拼成三角形，请问：有多少种剪法。题目先行进行了示例：剪成3 厘米、5 厘米和6 厘米的三段，3+5+6=14cm。本题的核心是对三角形图形中三边关系知识点的考察，解决此题的关键，是在熟稔上述知识点基础上，基于三角形三边关系构建解题模型：（1）两边之和大于第三边，那么，14÷2=7，任何一个边长，都不可以大于7；（2）假设长边为6，则还剩余8，可以分为：（4，4）（3，5）（2，6）等三种情况；（3）假设长边为5，则还剩9，可以分为（4，5）；（4）若长边为4，则尚余10，10÷2=5＞4，4 为长边的说法不成立。因此，最终还可以组成三角形有以下几种情况：（1）6，4，4；（2）6，2，6；（3）5，4，5 等三种形式。通过本题的学习，同学们在动手动脑尝试各种剪法的同时，也在反思自己对三角形边长关系的认知，在数学建模的解题过程中，形成数学思维的批判性吸收，以促进学生积极健康的数学核心思维养成。

五、从直观想象着手，培养学生数学思维创造性

直观想象是学生借助个人经验，通过直觉判断，将复杂的数学问题变得简明、形象，从而获取解决数学问题的思路，或直接预测出数学结果的过程。注重直观想象力培养，不仅是数学核心素养的前提，也有助于学生数学思维创造性提升。

以下题为例：将两个相同的直角梯形叠合在一起（如下图1中图a 所示），求阴影部分的面积。正常的解题思维，是进行图形切割，将下图图a 中的不规则阴影图形进行规则切分，以探寻解题之路。在课堂教学中，通过鼓励学生认真读题，充分发挥图形想象力，借助数学直观思维，探寻解题之道。经过几轮讨论，学生们很快发现了该题的解题思路：去除两个相同图形的重叠部分面积，阴影面积可以等价替换为图b 阴影部分面积，借助梯形公式，［（10-2）+10］×6÷2，很快得出结果54。

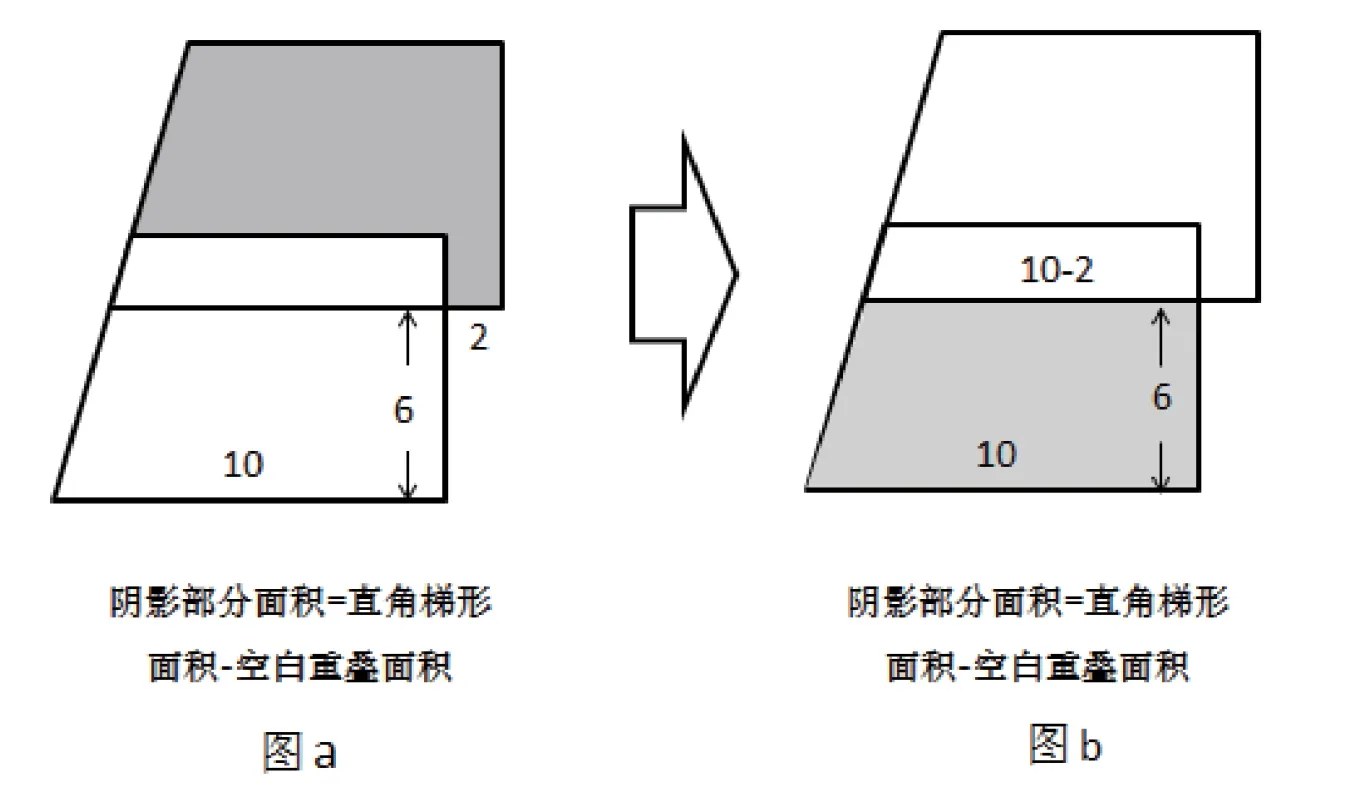
图1

总之，核心素养下，要聚焦学生思维品质的培养，只有在每一节课中夯实学生基础，循序渐进不断渗透，与时俱进，运用新的教学方式，精心设计课堂教学，充分调动学生的主动性，才能培养出小学生优秀的数学思维品质。