基于Richardson外推法的CFD离散误差分析*

左玲玉,司海青,李 耀,仇静轩,李 根,吴晓军,赵 炜

(1. 南京航空航天大学通用航空与飞行学院,江苏 南京 211100;2. 中国空气动力研究与发展中心,四川 绵阳 621000)

近年来,随着流体力学理论、数值方法以及高性能计算机技术的飞速发展,气动数值模拟技术(CFD)以其花费低、耗时短、损耗小等优点在航空航天领域发挥着越来越大的作用。然而,CFD技术要获得更广泛的应用及效益,对其可信度的要求也越来越高,所以,对CFD计算结果开展可信度研究十分必要,而可信度研究的基本内容和方法就是验证与确认(V&V)。

验证主要是对数值模拟过程中的误差进行分析,以验证仿真结果的准确性;确认主要是将模拟结果与实验数据进行比较,以评估数值模型与实际模型之间的相似性。国内外对CFD的验证与确认工作一直高度重视,迄今为止,大多数验证研究都是基于Richardson外推法获得插值解从而得到数值计算的误差估计;Reed等通过对高超声速飞行器二维和三维几何模型的机理识别以及CFD网格收敛性研究,最大程度地降低高超声速飞行器设计中各方面产生的不确定性;Lance等对混合对流进行了实验研究,比较了实验数据和模型输出,为CFD模型提供了完整的验证数据;Islam等对四种不同的船型进行验证与确认研究,使用基于安全系数和修正系数的方法估计算例的不确定性,虽然使用了相似的网格拓扑,但所有四个仿真计算都得到了不同的结果;于沛从算例的角度对验证确认的层次结构、算例的分类、选择等方面进行了分析说明;陈坚强等利用Richardson插值法对典型高超声速流动问题进行了网格收敛性研究,然后,利用不确定度分析方法开展了该问题的确认;康顺等总结了CFD模拟中的误差及估计准则,并以二维翼型为例介绍了如何进行误差估计和结果修正。通过总结分析各位专家学者们的研究发现,在验证与确认过程中针对数值模拟误差的研究占据着相当重要的位置,并且网格收敛性研究是必不可少的一部分。

1 CFD数值模拟误差

在采用CFD软件进行数值模拟时,模拟结果与真实结果之间存在一定误差,主要包括以下几个方面。1)物理建模误差:由于模型简化、控制方程、边界条件等引入的误差。2)离散误差:主要源于对数学模型和定义域的离散,包括离散格式的截断误差、边界条件设置不合理、网格质量较差等情况导致的离散误差增大。3)迭代误差:CFD软件数值模拟过程中采用松弛迭代法求解各类代数方程时随时可能产生的误差,包括不完全迭代或迭代的步数太少等。4)几何外形:包括数模与真实模型外形之间的差异和生成网格时几何修改或近似引入的误差。5)来流条件变化:CFD仿真模拟中由于来流参数变化所导致的不确定性会使计算结果产生一定的偏差。

在各种误差中,空间离散误差是其中最重要且最难估计的部分,在误差源中占较大比重,所以,离散误差估计是我们的研究重点,而网格收敛性研究是目前空间离散误差估计最为普遍的方法。

2 Richardson外推法

本文采用Richardson外推法对离散误差进行分析,该方法利用离散步长将离散解与精确解的关系用泰勒展开的级数形式表示:

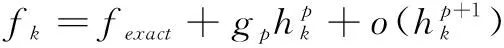
(1)

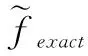
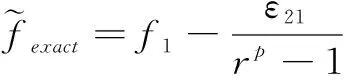
(2)

其中,收敛精度由下式确定:

(3)

同时可以得到网格上的误差估计:

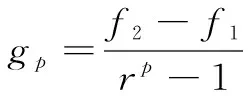
(4)

而网格细化比由下式定义:

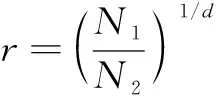
(5)

式中:是网格的网格单元数,为空间维数。由于求解过程中会忽略高阶项,所以,误差往往偏大,对式(2)添加一个修正因子来提高对误差估计的精度,具体为

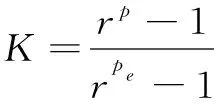
(6)

其中，是对高阶项的估计。所以,修正后可以得到精确解:

(7)

Roache将网格数值解的网格收敛指标()定义为

(8)

式中,为安全系数,对于三套网格,取=125,最后定义收敛率为

(9)

当0<<1时,属于单调收敛,当<0时为振荡收敛,而当>1时为发散,Richardson插值法进行离散误差计算时只对单调收敛问题有效。

3 CFD离散误差分析

3.1 NACA2412翼型CFD仿真计算

本文对NACA2412三维翼型进行CFD数值仿真,其0°、4°、8°、12°攻角下升力系数和阻力系数的具体实验数据如表1所示。

表1 升力系数和阻力系数不同攻角下的实验值

对模型进行了6种不同数量的网格划分,其中,前三种采用结构网格,后三种采用非结构网格,图1展示了采用O型网格划分情况,图2为非结构网格的划分情况,两种类型网格均在机翼前缘和后缘进行网格加密以便更好地捕捉流动特性。

图1 NACA2412结构网格划分细节图

图2 NACA2412非结构网格划分细节图

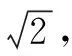
本文采用Fluent软件进行定常计算,湍流方程采用Spalart-Allmaras模型,马赫数=0.23,动量方程及湍流耗散率方程均采用二阶迎风离散格式,计算残差设置为10,经过约1200步迭代计算后各个计算模型均达到收敛条件,表2和表3对应于NACA2412翼型不同网格数量在0°、4°、8°、12°攻角时CFD计算得到的升力系数和阻力系数。将不同攻角条件下的CFD计算值与实验数据进行对比,发现随着网格尺度的变化计算结果单调收敛且处于渐进收敛域内,可以进行网格收敛性研究。

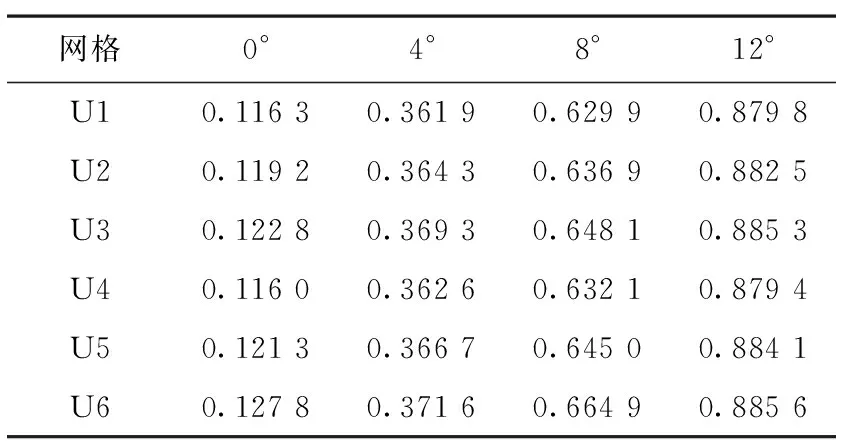
表2 不同攻角下升力系数的CFD计算值

表3 不同攻角下阻力系数的CFD计算值

3.2 Richardson 外推法结果分析

为了展示网格类型以及网格粗密程度对误差估计精度的影响,将6套网格分为两组进行研究,其中,网格U1、U2和U3为网格研究组1,网格U4、U5和U6为网格研究组2,表4为利用公式(9)计算得到的两组网格不同攻角条件下的网格收敛判断。针对升力系数的计算,在0°、4°及8°时,网格研究组1(U1～U3)和网格研究组2(U4～U6)均为单调收敛,可以采用Richardson 插值法来估计其升力系数的计算误差,但网格研究组2(U4～U6)在12°攻角时发散,不能进行误差估计。对于各个攻角的阻力系数的收敛性计算,两个网格研究组合在小于最大升力攻角12°时均为单调收敛,可进行误差估计,在12°攻角时都属于振荡收敛,无法进行阻力系数的误差估计。

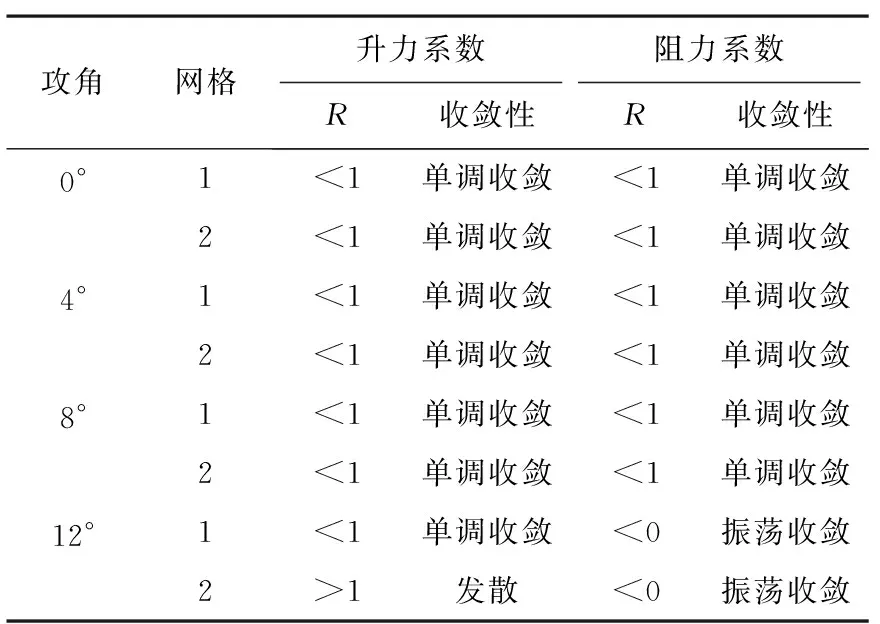
表4 升阻力系数的收敛性判断

针对0°、4°、8°攻角条件下升阻力系数,计算得到网格研究组1、2对应的离散误差估计以及网格收敛指标值(下标1代表研究组1升力系数对应的计算结果,下标1代表研究组1的阻力系数对应的计算结果,依此类推),具体见表5。

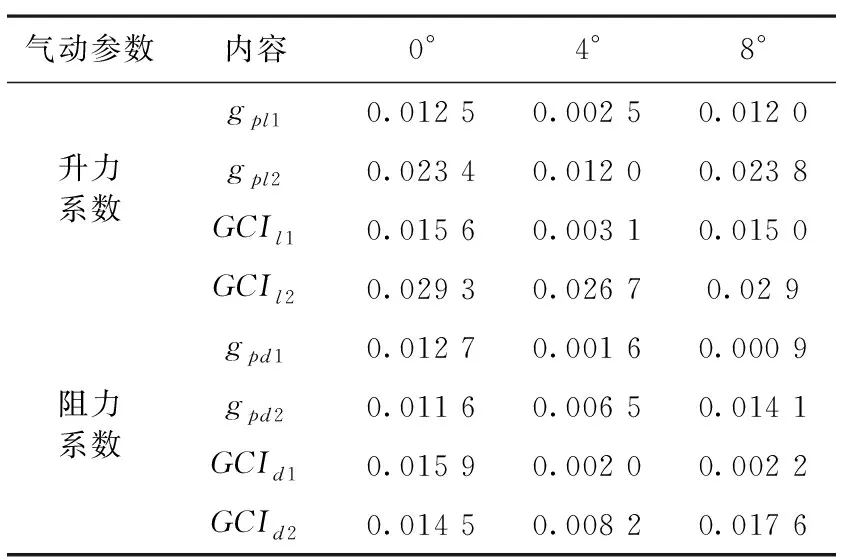
表5 不同攻角下网格组合升阻力系数的分析结果

结果表明,两个网格研究组的网格误差和网格收敛指标计算结果接近,但结构网格的网格误差以及网格收敛指标整体上均小于非结构网格,同时网格类型的改变对升力系数的影响更大。

对0°、4°和8°攻角下升阻力系数计算值求解得到收敛精度如表6所示。

表6 不同攻角下网格组合升阻力系数的收敛精度

根据计算结果发现，同一攻角条件下升阻力系数收敛精度相差不大,说明CFD计算结果较为准确,同时网格研究组1的收敛精度大于网格研究组2的收敛精度,可见结构网格的离散解能以更快的速率接近精确解。所以,求解修正系数时,对于网格研究组1根据经验取2,而对于网格研究组2,假定结构网格组合达到对应的网格无关解,所以其各个攻角下的取其对应的网格研究组1计算得到的收敛精度,由不同攻角下各网格组合升阻力系数收敛精度和对应的修正系数进一步求解得到修正后的精确解。

图3和图4给出了0°、4°、8°攻角下不同网格研究组合随网格数量变化的CFD计算值、修正后的精确解及其实验数据的对比图。其中，黑色实线为实验值,蓝色点划线为6套网格的CFD计算值,红色双点划线和绿色划线对应于网格研究组修正后的精确解F1、F2,这两条点划线所覆盖的网格长度对应于各自进行误差估计时所采用的网格研究组。

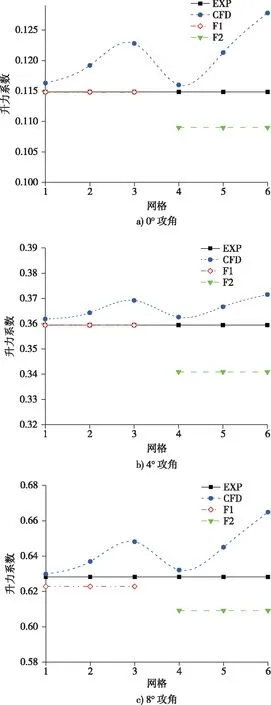
图3 不同攻角下升力系数对比图

图4 不同攻角下阻力系数对比

根据图3中的结果可见,在0°、4°、8°这三种攻角条件下网格研究组1计算的升力系数的精确解与实验值的误差均在2%以内,说明该种类型网格进行计算时随着网格数量的增加对机翼尾迹以及边界层处的流动情况模拟效果较为精确,结果趋于网格无关值,网格尺度对计算结果的影响逐渐消失。而网格研究组2由于CFD计算值随网格单元数的变化有较大差异,所以计算所得的精确解与实验值的误差远大于网格研究组1。

由图4可知,网格研究组1对于阻力系数的计算值也随着网格数量的增加逐渐达到网格无关解,但是本文主要考虑修正网格尺度变化所引起的误差,忽略了可能涉及的不完全迭代误差、时间步长误差等情况,所以所得的精确解与实验值仍有差异。对于网格研究组2,在4°攻角时CFD计算所得的阻力系数随着网格数量的增加更加趋近于网格无关解,而0°和8°攻角下得到的精确解与实验值的误差较大,说明对于网格研究组2,目前的网格单元数仍未达到最优效果,需要对网格尺寸进行调整,通过更加精细的网格来获得更加精确的计算结果。除此之外,可能还需要对模型本身或计算条件、边界条件等进行进一步的改进。

4 结束语

本文为评估网格类型及网格数量对NACA2412机翼CFD离散误差的影响,对其三维模型分别进行结构、非结构两种类型共6套网格的划分,并进行了三维定常流场数值模拟,结合Richardson外推法和GCI网格收敛指标法对升力系数、阻力系数进行了离散误差估计,对比分析了CFD计算结果、修正后的精确值、实验数据,完成了网格收敛性研究并得到结论:结构网格与非结构网格模型的离散误差有较大差异,网格类型的改变对升力系数的影响更大,两种方法计算所得的非结构网格升力系数的误差为结构网格误差的两倍左右;随着网格单元数的增加,各个攻角条件下结构网格的升阻力系数均比非结构网格更接近于网格无关值。