目标数未知条件下分布式被动传感器信息关联模型
李洪瑞
(江苏自动化研究所,江苏 连云港 222061)
信息关联是信息融合中的一个重要概念、难点和关键技术,它起源于单传感器多目标跟踪,并随各种信息融合系统的发展而发展,在不同的信息系统中依据不同的信息融合处理结构而以多种形式存在,例如分布式信息融合中的航迹与航迹的关联、集中式信息融合中的测量与航迹的关联,传感器信息处理中的测量与测量的关联、视频跟踪中的图像关联,航迹段的关联等。由于关联技术直接影响到信息融合系统的性能,因此一直受到广泛关注,并且针对具体融合系统已有许多处理办法,如用于量测关联的集合论描述法、近邻域法、多假设关联、联合概率数据关联以及神经网络关联等。多传感器信息关联本质上离不开多维分配模型,该模型的求解算法是相当复杂的,是NP复杂性难题,在目标数和传感器数较多时一般难以进行实时求解,因此针对多维分配模型求解的各种算法应运而生,当前,多维分配模型的研究众多但还没有原理上的数学求解算法。而许多融合算法则是以关联为前提,利用所有同源信息进行融合估计以期得到目标状态的最优化估计。
分布式被动传感器探测系统由分布于一定区域的被动传感器组成,以求弥补单被动传感器在探测范围、探测信息维度上固有的缺陷,实现区域监视。相比主动探测系统,分布式被动传感器系统中,由于被动探测信息的不完全性,不同传感器测量信息或传感器不同时段探测信息不适合直接采取比较分析的处理方法进行关联处理,导致多被动传感器信息融合中的关键技术之间存在耦合或相悖,如关联与定位、关联与估计,此外由于被动探测信息的不完全性,这些问题给分布式被动传感器信息融合系统的建模与设计增加许多难度,相关技术的研究也更具有挑战性。文献[9]将被动传感器测量进行两两交叉定位,将关联问题转化为交叉点分配问题,文献[11]将多传感器信息融合按一定准则分解为每个节点仅需要处理双传感器信息的多节点信息融合,然后用神经网络求解关联问题,避免了多目标关联中的组合计算。在前面提到多维分配模型研究中,其中多维指标的估计一般都依赖目标参数估计(即要求观测系统是可观测的),一些以目标数已知为前提,但在被动系统中很多情况下是不能进行这种估计的,因为观测平台并不进行有效机动或根本就不机动,实际上对于多传感器纯方位系统也存在可观测性问题。
实际探测环境中存在多少目标是不确定的,各传感器探测范围以及干扰和障碍遮挡等各种原因,造成各传感器探测的目标个数不同,传感器共同探测和独立探测的目标数难以确定。在分布式被动传感器信息系统中,当目标数未知时,一方面各传感器之间的信息组合的复杂度增加,求解更加困难;另一方面,存在单传感器探测的目标信息,由于目标状态不可观测,因此难以使用这些信息建立优化(如极大似然估计)指标,使各种关联分配算法失效,这给关联建模及求解带来巨大困难。例如,图1(图中仅标示了部分虚假目标)中,实际目标数有5批,在3个传感器探测情况下,目标分别被3个、2个或1个传感器探测到,但是通过方位线进行交叉则有许多虚假的目标出现,各传感器探测方位的关联关系如表1所示,融合系统需要把这些关联关系确定出来,才能后续进行目标估计和形成态势。在传感器和目标数更多的时候,目标个数与参数估计以及形成态势的过程更加复杂。
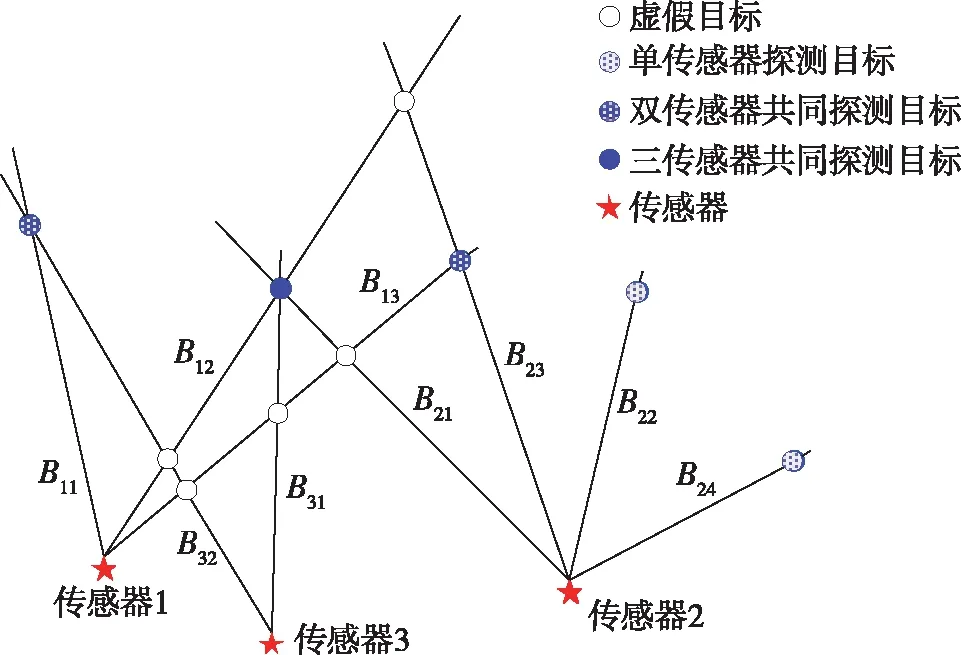
图1 三被动传感器探测5个目标方位示例

表1 三传感器探测方位之间的关联关系
在多传感器情况下,通常采取适当的体系结构,例如混合式的有序分层信息融合体系结构等,将信息系统分解为每个节点仅需要处理双传感器信息的多节点信息融合系统,避免多传感器信息的多重组合。因此,双传感器的信息融合是基础,本文主要研究目标数不确定情况下双被动传感器信息融合中的关联建模问题。
1 问题描述
设被动传感器1探测到个目标的方位、被动传感器2探测到个目标的方位,经传感器各自处理后输出方位序列信息,传感器共同探测到的目标及其个数未知,因此两个传感器探测形成的态势中目标总个数也是未知的。信息关联要求确定传感器1和传感器2共同探测到的目标(它们的运动参数可以估计出),以及各自探测到但无关联的目标(这些目标的运动参数一般难以估计),进而确定两传感器探测情况下的目标态势。

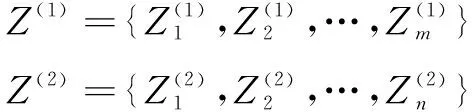
(1)
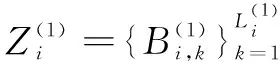
为了描述两个传感器测量信息之间的关联关系,先给出可行关联矩阵定义。
1 设(+1)×(+1)阶矩阵:

(2)
满足:
1)各元素取值为0或1;
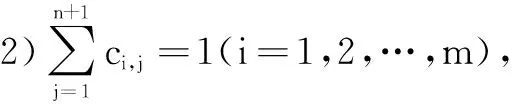
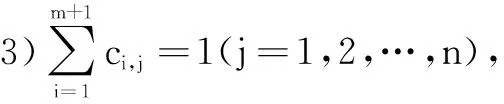
则称矩阵(,)(+1)×(+1)为(+1)×(+1)阶可行关联矩阵,简称可行关联矩阵。
对于一个可行关联矩阵=(,)(+1)×(+1),若,=1,则:1)当1≤≤、1≤≤时,表示传感器1的目标与传感器2的目标关联;2)当1≤≤、=+1时,表示传感器1的目标为独立观测;3)当=+1、1≤≤时,表示传感器2的目标为独立观测。+1,+1没有实际意义,可取为0。可见,每个可行关联矩阵确定了两个传感器探测目标之间的关联关系,因此一个可行关联矩阵表示了两传感器测量信息之间的一个可行关联解。可行关联矩阵中等于1的元素的个数即为融合态势中目标总个数。所有(+1)×(+1)阶可行关联矩阵构成的集合记为,。
可行关联矩阵的前行、前列构成的子矩阵(,)×中等于1的元素的个数为两传感器共同探测的目标个数,这些目标的运动参数可以解算出来。可行关联矩阵的第+1行和第+1列中等于1的元素的个数为仅单个传感器探测的目标,一般不能得到它们的运动参数。
例如在如图1及表1所示的探测情况下,传感器1和传感器2探测信息之间正确的可行关联矩阵为

(3)
这表明传感器1探测的方位2、3分别与传感器2探测的方位1、3关联,传感器1探测的方位1、传感器2探测的方位2、4分别为2传感器各自独立探测的目标方位,因此目标总数为5个。
按照可行关联矩阵的定义,信息关联问题即为求解正确的可行关联矩阵的问题,本文主要利用双传感器目标定位跟踪原理以及传感器方位测量方程,构建代价函数,并证明代价函数的极值定理,构建解关联问题的最优化模型。最后给出数字计算示例,说明所提出的优化指标和建立的模型的有效性。
2 关联模型
令代价函数
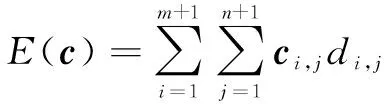
(4)
式中,,表示:当1≤≤、1≤≤时,,为在传感器1探测的方位与传感器2探测的方位关联的假定下,双传感器测量信息的联合极大似然函数的负对数;当1≤≤、=+1时,,为在传感器1探测的方位不与传感器2探测的任何方位关联的假设下,测量信息的极大似然函数的负对数;当=+1、1≤≤时,,为在传感器2探测的方位不与传感器1探测的任何方位关联的假定下,测量信息的极大似然函数的负对数,即
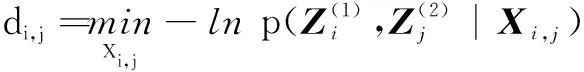
(5)
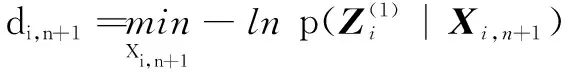
(6)

(7)
(=1,2,…,;=1,2,…,)
式中
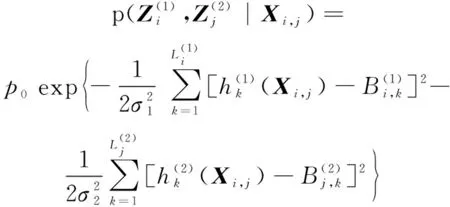
(8)
式中为概率归一化常数;,为在传感器1探测的方位与传感器2探测的方位关联的假定下,所探测目标的状态向量。在目标匀速直线运动假定下,目标运动参数为4个,因此目标状态取为由目标初始位置坐标、航速、航向组成的4维向量。
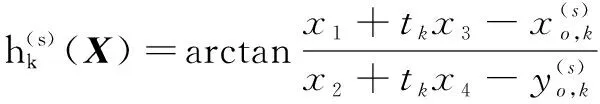
(9)

+1,+1没有实际意义,可取值0。对于被动传感器,一般不能从方位序列得到目标的状态估计,因而也不能从式(6)、(7)得到,+1、+1,。为此,利用等效匀速直线观测器探测方位的分式线性计算式引入如下计算方法。令

(10)
(=1,2)
式中,,,是待估参数,它们构成的3维向量记为。由此得到,+1、+1,的估计模型:
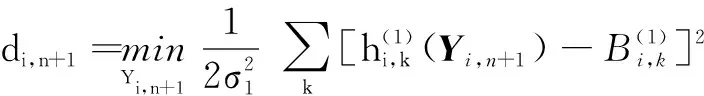
(11)
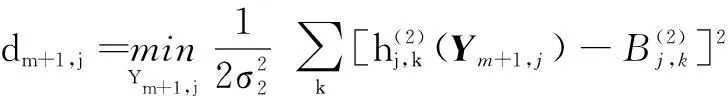
(12)
(=1,2,…,;=1,2,…,)
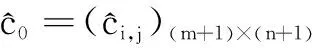


(13)
关于代价函数()的极值,有如下定理。

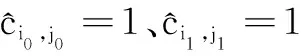

(14)
记
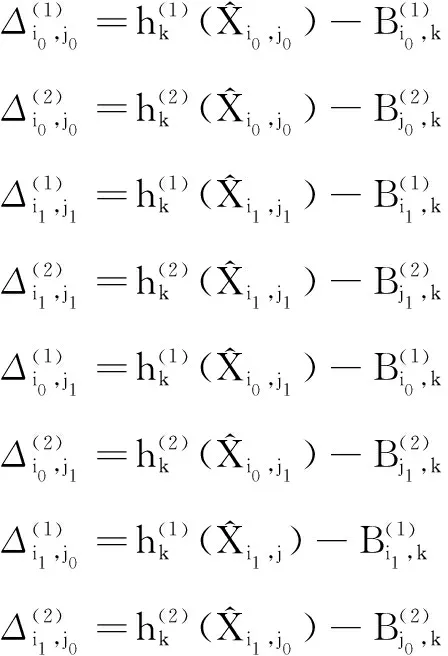
(15)
因此
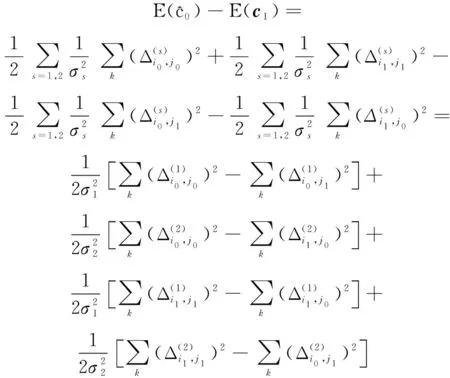
(16)

从定理1,建立关联求解的最优化模型如下:

(17)
其最优关联解为
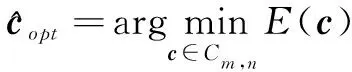
(18)
3 数字计算
本节给出一个双传感器探测不同目标情况下,关联矩阵、互相关指数、代价函数值的算例,以对模型应用和代价函数极值定理进行展示与验证。
1)模拟态势参数设置
模拟目标运动参数初始值如表2,共模拟17批真实目标,传感器1探测到目标1-12(共12批目标)、传感器2探测到目标5-17(共13批目标),目标5-12(共8批目标)是两传感器共同探测目标,目标1-4仅被传感器1探测到,目标13-17仅被传感器2探测到。在未知目标数的情况下,可能的目标数在13-25之间,可行关联解的个数为2.029 764×10。
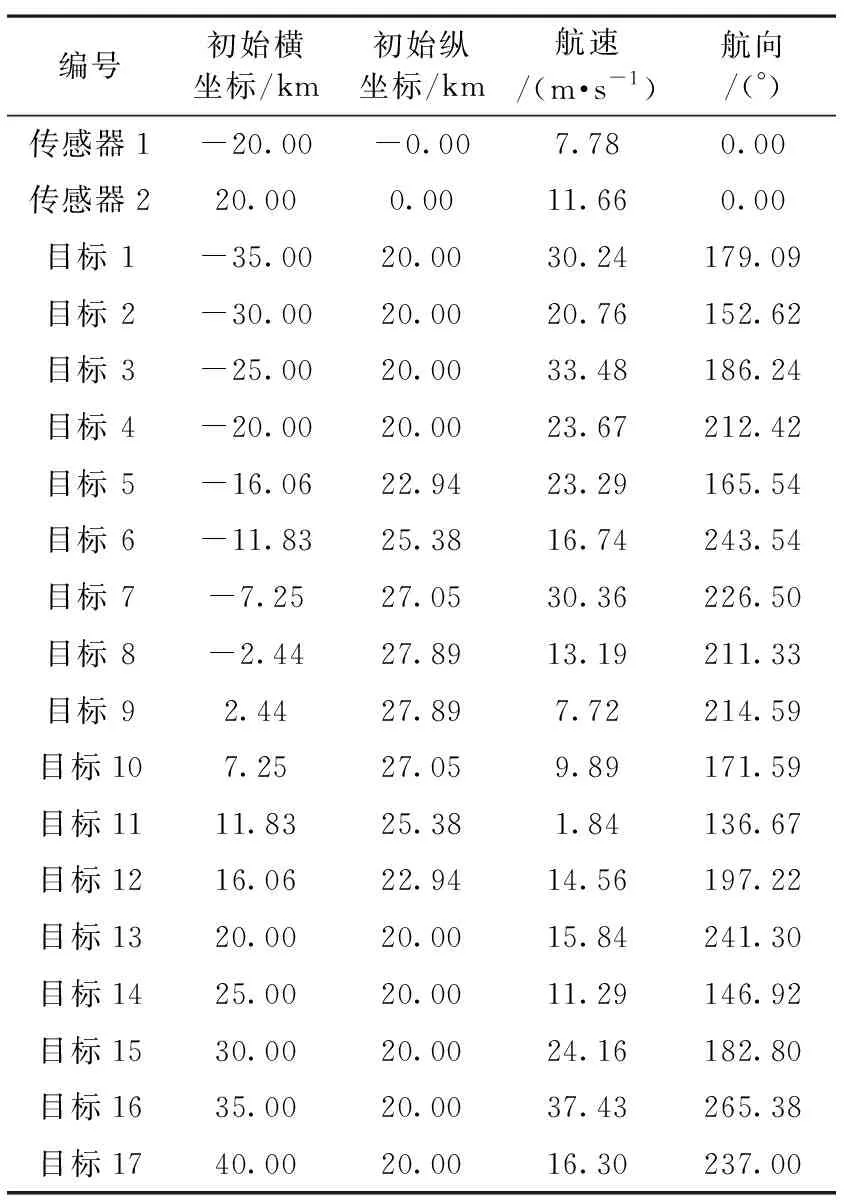
表2 模拟态势初始参数

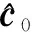

(19)
2)互相关指数计算
依据式(5)、(6)、(7),采用最小二乘估计算法计算互相关指数(矩阵),去除常数后得计算结果如下:
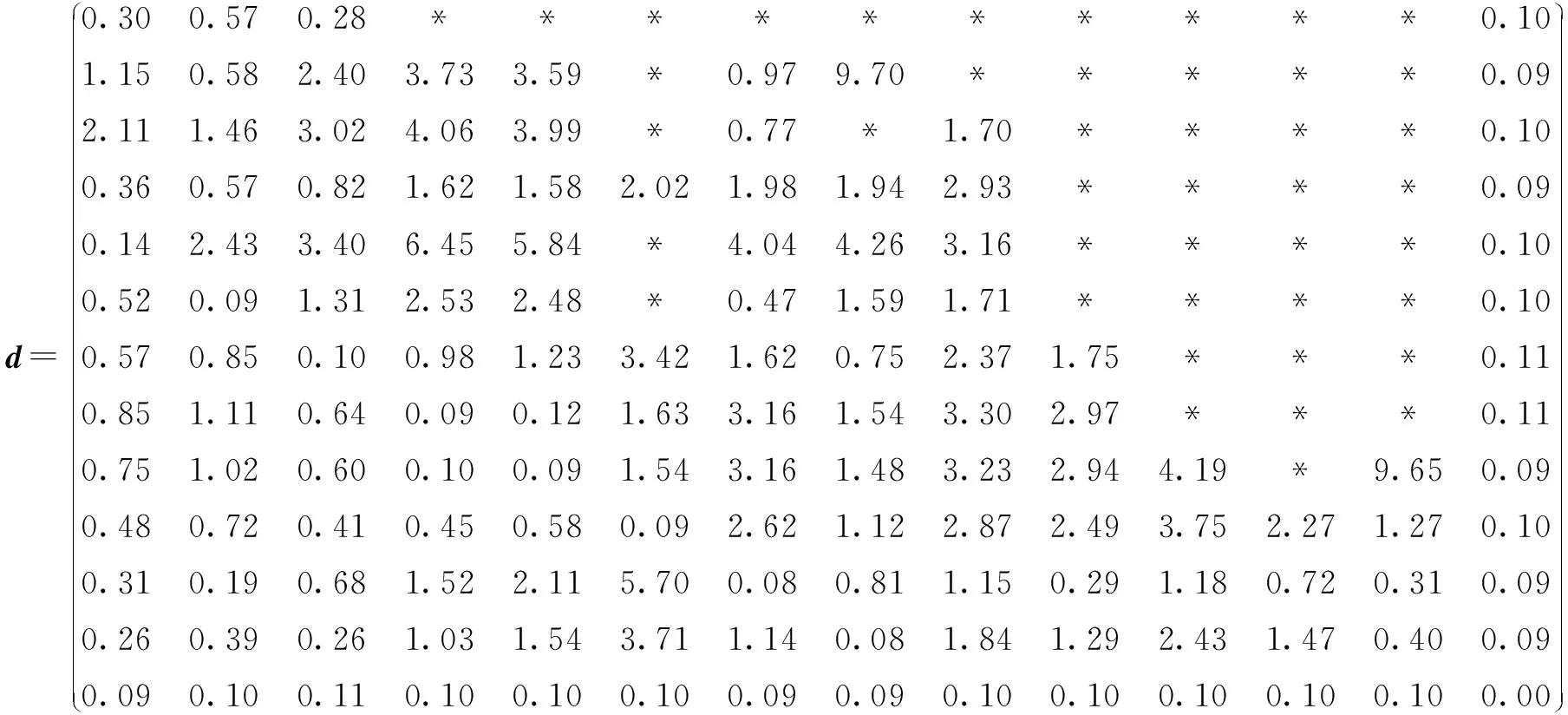
(20)
上式中符号*表示大于等于10的数。
3)代价函数值计算

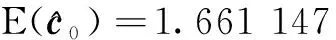
(21)
从可行关联解空间进行10次(约占样本总数的5)随机取样计算代价函数值(如图2所示为其中1 000 个的计算结果),结果显示式(21)是最优的,这进一步验证了定理1,也验证了本文所建最优关联模型的有效性。
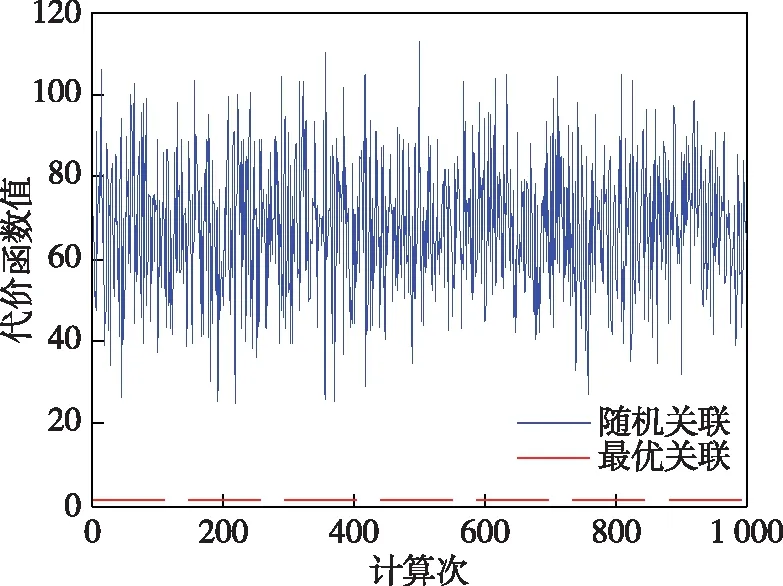
图2 代价函数值及其最小值
为了进一步检验模型的有效性,对表2中给出的模拟态势(包括传感器和目标)初始参数进行随机扰动,扰动参数设定为初始位置坐标、速度、航向的均方差分别为3%、速度0.8 m/s、航向1°,按上述步骤2)和3)进行100次的互相关指数、最优可行关联矩阵的代价函数值和随机取样的代价函数值的计算,并对计算结果进行统计。计算结果为最优可行关联矩阵的代价函数值为最优代价函数值的次数为99。由此可见,本文所提出的最优关联模型是有效的。
4 结束语
传感器信息关联历来是信息融合的难点和关键,其性能直接影响融合系统的性能。对于分布式被动传感器信息融合系统,还存在目标定位问题及两者铰链带来的难题,进而导致关联问题建模与求解困难。本文通过确定互相关指数的计算方法,定义了代价函数,建立了2个分布式被动传感器间信息关联求解的数学模型,理论证明和数字计算展示了代价函数的极值定理,从而将传感器信息的关联问题转化为求代价函数的极值问题,所建模型对解关联问题具有重要意义。

