基于线性自抗扰的DC/DC升压变换器的控制策略研究

崔一然， 徐红梅

(延边大学 工学院， 吉林 延吉 133002)

0 引言

DC/DC升压变换器是一种通过调制脉冲宽度来获取期望输出电压的电力变换装置.由于该装置具有结构简单、体积小、效率高等优点，因此在并网发电系统、航空航天、电动汽车、工业仪表等领域被广泛作用[1-3].为降低负载和输入电压扰动对输出电压的影响，学者们对DC/DC变换器进行了大量的研究.2022年，周讯杰[4]使用PI控制算法设计了一种双闭环反馈控制器，该控制器虽然可以稳定输出电压，但PI控制的误差反馈会使控制量延迟.目前，除使用PI控制器外，提高系统稳定性的控制方法还有滑模控制[5]、模糊神经网络预测[6]等，虽然这些方法优于传统的PI控制，但由于它们过于依赖控制系统模型的参数以及固有频率等，因此其应用仍受到一定的限制.

自抗扰控制技术(active disturbance rejection control,ADRC)是一种基于现代控制理论的控制策略，因其具有灵敏性、易用性以及基本不依赖对象的数学模型等特点而受到学者们的广泛关注[7].2018年，杨惠等将自抗扰控制技术引入于DC/DC变换器中，研究显示该非线性自抗扰控制器(NLADRC)可以有效地提高控制系统的效率和抗干扰能力；但由于该控制器的控制参数只能通过试错法和自身经验得到，因此其应用受到一定的限制[8-9].2018年，高志强等提出了一种线性自抗扰控制方法(LADRC)，该方法可大大简化ADRC参数的整定，并可为其他学者研究自抗扰控制提供良好参考[10].基于上述研究，本文针对DC/DC升压变换器设计了一种基于线性自抗扰控制(LADRC)的双闭环控制策略，并通过仿真验证了其具有良好的控制效果.

1 线性自抗扰控制器的设计

1.1 Boost电路原理

图1为Boost电路图.图中，Boost电路由直流电源Ui、储能电感L、电子开关管S、二极管VD以及滤波电容C等组成.当Ui输入高电平时，开关管S导通，电源给电感L充电(电感电流逐渐增大，电感储能增加)，二极管VD截止，电容C单独向负载R供电(两端的电压不断减小)；当Ui输入低电平时，开关管S关断，续流二极管VD导通，电源和电感L同时为电容C充电(电容C两端的电压逐渐增加)和向负载R供电.

1.2 数学模型的建立

工作状态1： 可控开关S导通、二极管VD关断时，电感电流iL和输出电压vo的状态方程为:

(1)

工作状态2： 可控开关S关断、二极管VD导通时，电感电流iL和输出电压vo的状态方程为:

联立式(1)、(2)后采用状态平均法对式子进行矩阵变换可得：

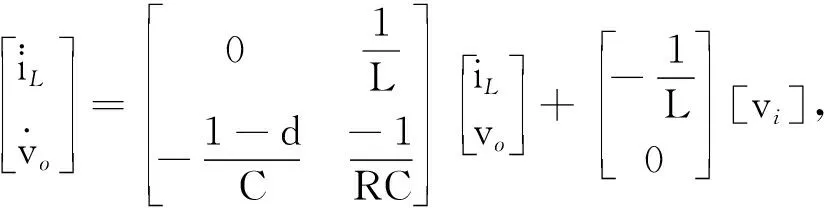
(3)

式中d为占空比.对式(3)进行频域变换和小信号建模可得如下Boost电路占空比到输出电压的传递函数：

(4)

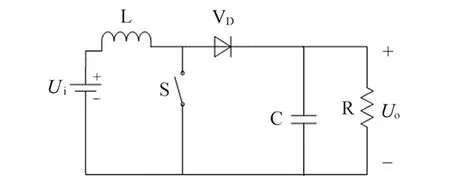
图1 Boost电路图

1.3 系统稳定性分析

为了验证开环系统的稳定性，利用式(4)得到的开环传递函数绘制了Boost开环传递函数的伯德图，如图2所示.由图可以看出，该系统的相位裕度为-8.22°，幅度裕度为-6.35 dB，穿越频率约为8.96 kHz.由此可知，该系统不稳定，且响应速度较慢.为了提高该系统的性能，本文使用串级LADRC对其进行补偿矫正.

1.4 PI模型的建立

PI控制的基本结构如图3所示，其中Gid(s)是占空比到电感电流的传递函数，Gvi(s)是电感电流到输出电压的传递函数，电感电流的参考值由电压环PI控制器的输出给定.

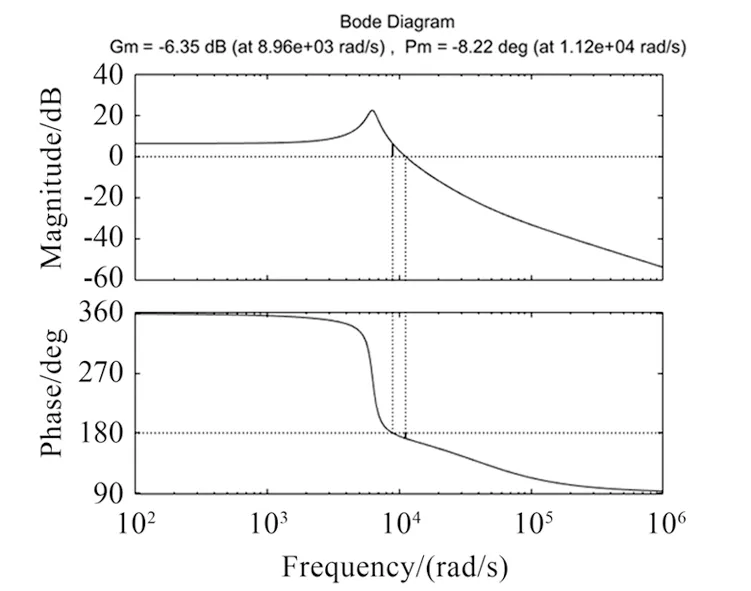
图2 Boost开环传递函数的伯德图

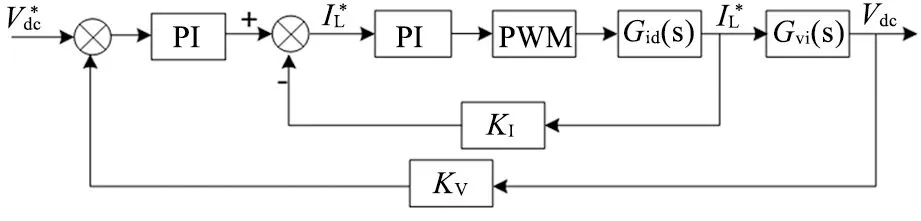
图3 双环PI控制的结构

2 基于LADRC的双闭环Boost电路的控制策略

2.1 DC/DC升压变换器自抗扰控制策略的设计

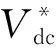
Gin(s)=Gc2(s)/(1+Gc2(s)Gid(s))，

(5)

其中Gvd(s)是占空比到输出电压的传递函数，Gvi(s)是占空比到电感电流的传递函数.根据式(5)，本文将系统传递函数定义为：

2.2 LADRC模型的建立

LADRC控制框图如图5所示，其中扩张状态观测器(LESO)用于估计系统的总干扰，z1、z2和z3是LESO的输出，kp、kd和b0是LADRC的参数.在本系统中，LESO的主要作用是精确跟踪实际电压回路的采样信号Vdc以及估算出受控系统的内外扰动量.

图4 二阶线性ADRC的结构

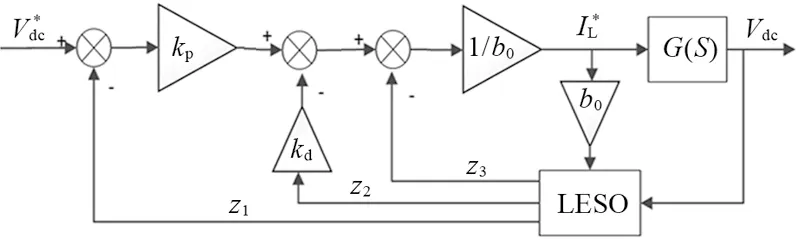
图5 LADRC控制框图

根据LADRC控制框图(图5)，本文将LESO定义为：

(7)

其中β1、β2和β3是观测器增益，b0是补偿系数，z1是Vdc的跟踪信号，z2是z1的差分信号，z3是系统总扰动的跟踪信号.由公式(7)可知，通过选择适当的观测器增益，LESO可以实时跟踪系统的变量.

根据LADRC原理得到的状态反馈控制律为：

(8)

其中kp和kd是LADRC的可调参数.由公式(8)可知， LADRC的参数及观测器增益会直接影响控制器的性能.根据文献[11]提出的线性参数调整方法，本文将上述参数简化为：

(9)

(10)

其中：参数ω0是观测器的带宽，参数ωc是控制器的带宽.研究[12]显示：ω0的大小与LESO跟踪速度有关；ω0越大，跟踪信号z1对输出电压响应就越快，但ω0过大会使速度响应发生振荡，进而会造成系统的输出变得不稳定.

补偿后的bode图如图6所示.由图6可知，相位裕量从-8.22 dB提升到了11.1 dB，幅值裕量从-6.35 deg提升到了21.8 deg，该结果表明系统经补偿后具有良好的稳定性.

3 基于LADRC的双闭环控制系统的仿真验证

为了验证本文提出的控制策略的有效性，将本文提出的控制策略与经典双回路PI控制策略进行了对比(利用Matlab/Simulink仿真实验).图7为LADRC控制的Boost电路图，图8为PI控制的Boost电路图，图9为双环LADRC电路的仿真模型.仿真参数为：输入电压Ui为12 V， 储能电感L为1 mH， 滤波电容C为920 μF， 占空比d为0.5， 开关频率f为300 kHz.电流环观测器的带宽ω0为270， 控制器的带宽ωc为165， 补偿系数b0为543.5； 电压环观测器的带宽ω0为8 800， 控制器的带宽ωc为1 600， 补偿系数b1为24 000.

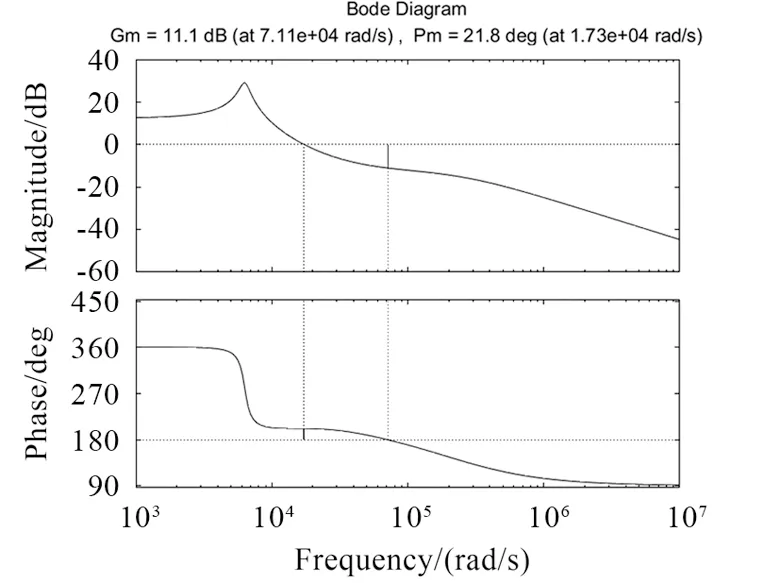
图6 Boost闭环传递函数的bode图

3.1 状态响应特性

图10为LADRC系统和PI控制器的输出电压波形.由图可知，LADRC系统到达稳态的时间(约0.1 s)及其超调量显著低于PI控制系统，由此表明LADRC系统的稳定性显著优于PI系统.

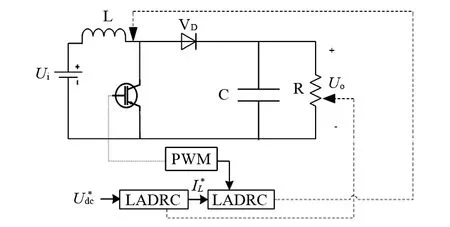
图7 LADRC控制电路图

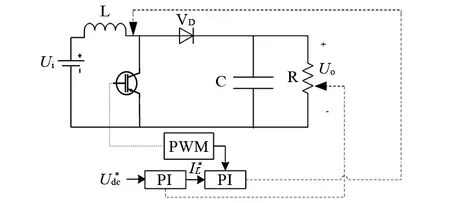
图8 PI控制电路图

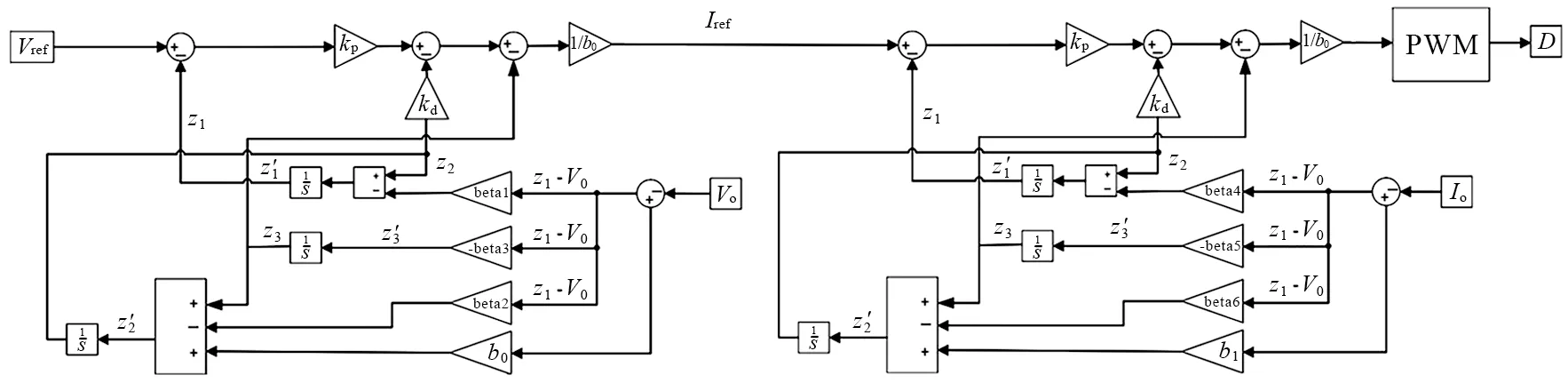
图9 双环LADRC电路的仿真模型

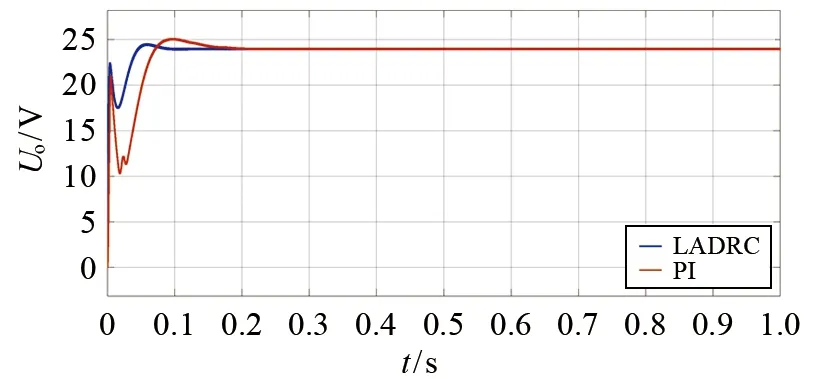
图10 稳态时输出电压的波形图

3.2 瞬态响应特性

1)输入电压扰动时的瞬态响应特性.在0.3 s时将输入电压由12 V变为10 V时两种控制系统的输出电压如图11所示.由图可以看出：本文提出的控制策略的输出电压由24.0 V降至22.7 V， 超调量为2.5%， 在0.36 s时达到稳定值(24.0 V)； PI控制策略的输出电压由24.0 V降至22.1 V， 超调量为7.9%， 在0.46 s时达到稳定值(24.0 V).这表明，在受到该输入电压干扰时，本文所设计的控制策略的输出电压响应波动幅值和输出电压达到稳定的时间均显著优于PI控制策略.

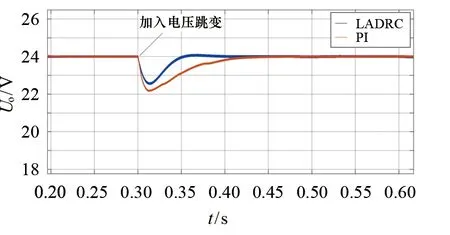
图11 电压扰动时的瞬态响应

为了进一步验证本文所提出的控制策略的瞬态响应特性，在0.3 s时将输入电压由12 V变为8 V.改变电压后的两种控制系统的输出电压响应曲线如图12所示.由图12可以看出：本文提出的控制策略的输出电压由24.0 V降至21.2 V， 超调量为11.6%， 在0.07 s时达到稳定值(24.0 V)； PI控制策略的输出电压由24.0 V降至20.1 V， 超调量为16.2%， 在0.24 s时达到稳定值(24.0 V).该结果与上述实验结果基本一致，由此进一步表明本文所设计的控制策略在受到输入电压干扰时具有良好的抗干扰性和稳定性.

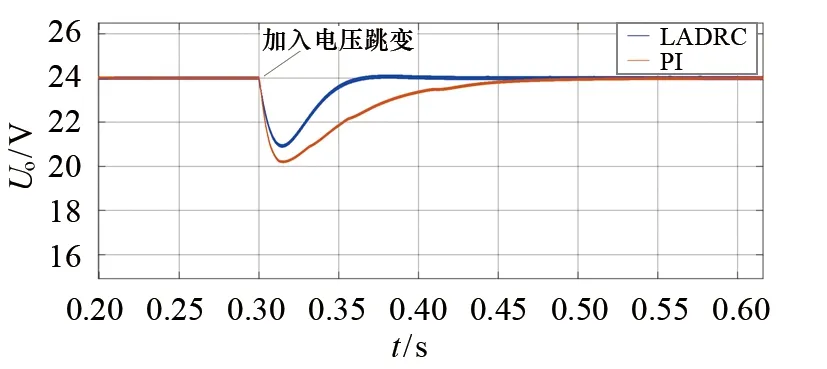
图12 电压扰动时的瞬态响应

2)负载扰动时的瞬态响应特性.在0.3 s时将负载阻值由50 Ω跳变到30 Ω，由此得到的两种不同控制策略的输出电压和负载电流的响应曲线见图13.由图13可以看出：稳态后输出电压为24.0 V， 负载电流为1.3 A； 加入负载后，负载电流由1.3 A跳变至2.1 A.同时还可以看出，本文提出的控制策略的输出电压和电流响应波动幅值均低于PI控制策略，且响应速度更快.这表明，在受到负载扰动时，本文所设计的控制策略的稳定性和抗干扰性显著优于PI控制策略.

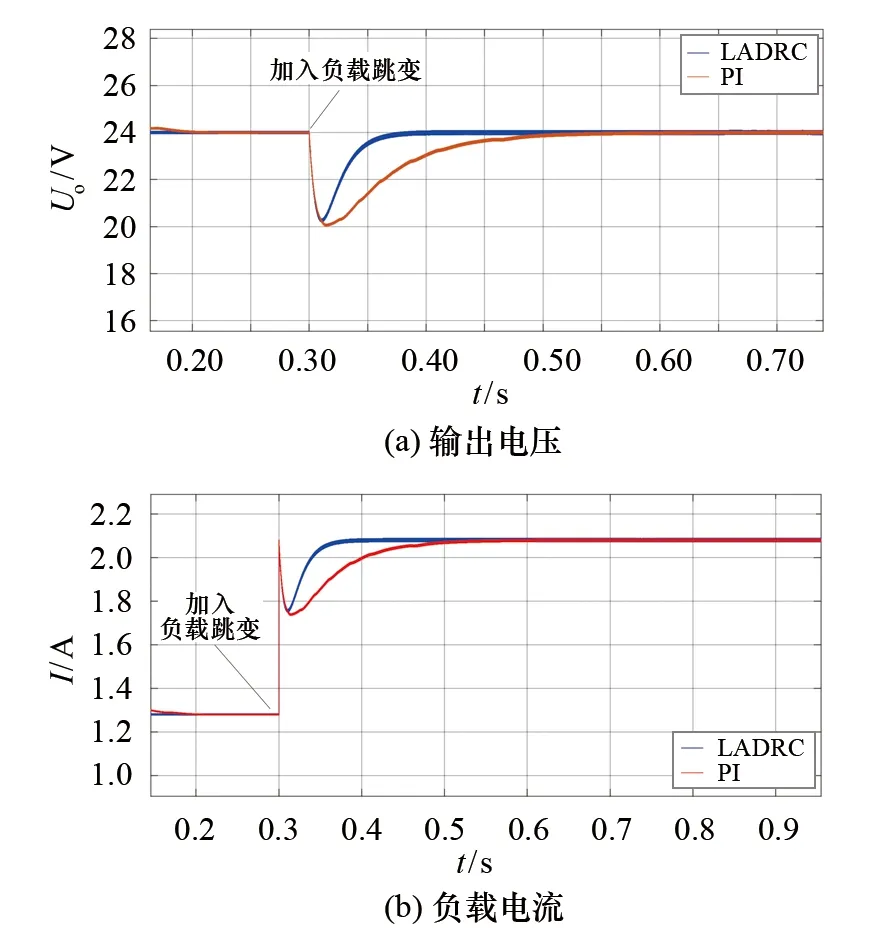
图13 负载扰动时的瞬态响应

4 结论

对本文提出的双环LADRC控制策略进行仿真实验表明，该控制策略在面对负载电阻和输入电压发生突变干扰的情况下，其抗干扰能力和快速响应能力显著优于PI控制策略.因此，本文提出的控制策略在DC/DC变换器的控制中具有良好的应用前景.在今后的研究中，我们将尝试将该控制策略应用到光伏储能系统中，以此探讨其对光伏储能系统的稳定作用.